Решение задач программирования в пакетах математических программ MS Excel, Mathcad, Mathematica

Министерство образования и науки РФ

федеральное государственное образовательное учреждение

высшего профессионального образования

«Российский экономический университет имени Г. В. Плеханова»

Факультет математической экономики, статистики и информатики

Кафедра информатики

КУРСОВАЯ РАБОТА

по дисциплине «Информатика и программирование»

на тему:

«Решение задач программирования в пакетах математических программ MS Excel, Mathcad, Mathematica»

 Выполнила: студентка 1 курса ФМЭСИ, 417 группы

Лазарева Оксана

Руководитель: д. ф.-м. н., профессор

Родионов Василий Николаевич

г. Москва

2016

Содержание.

Введение………………………………………………………………………….........................3

1.      Постановка задачи……………………………………………………………………..3-4

2.      Математическая модель……………………………………………………………….4-5

3.      Методы решения……………………………………………………………………….5-7

4.      Решение в MS Excel………………………………………………………………….7-10

5.      Решение в Mathcad………………………………………………………………….10-16

6.      Решение в Mathematica……………………………………………………………..16-17

7.      Анализ найденных решений………………………………………………………..17-18

Заключение……………………………………………………………………………………...18Список использованной литературы………………………………………………………….18

Введение.

В последние годы в прикладной математике большое внимание уделяется новому классу задач оптимизации, заключающихся в нахождении в заданной области точек наибольшего или наименьшего значения некоторой функции, зависящей от большого числа переменных. Это так называемые задачи математического программирования, возникающие в самых разнообразных областях человеческой деятельности и, прежде всего, в экономических исследованиях, практике планирования и организации производства. Изучение этого круга задач и методов их решения привело к созданию новой научной дисциплины, получившей позднее название линейного программирования. Линейное программирование - наиболее разработанный и широко применяемый раздел математического программирования. Это объясняется следующим:

• Математические модели очень большого числа экономических задач линейны относительно искомых переменных;
• Эти типы задач в настоящее время наиболее изучены;
• Для них разработаны специальные конечные методы, с помощью которых эти задачи решаются, и соответствующие стандартные программы для их решения на ЭВМ;
• Многие задачи линейного программирования, будучи решенными, нашли уже сейчас широкое практическое применение в народном хозяйстве;
• Некоторые задачи, которые в первоначальной формулировке не являются линейными, после ряда дополнительных ограничений и допущений могут стать линейными или могут быть приведены к такой форме, что их можно решать методами линейного программирования.

Постановка задачи.

Вариант 14.

Стоимость товаров трёх видов меняется с течением времени по следующим законам:

·         для товара первого вида (в количестве x₁) →  (3 + 2 * t),

·         для товара второго вида (в количестве x₂) →  (7 - t),

·         для товара третьего вида (в количестве x₃) →  (6 - t).

Требуется найти максимум стоимости всей партии товаров при изменении времени t = 0, 1, 2, 4, 5 и дополнительных ограничениях, задаваемых условиями хранения товаров:

 

2 * x₁ + x₂ £ 620,

2 * x₂ + x₃ £ 570,

х₁ + x₂ £ 310.

Математическая модель.

Общая форма математической модели задачи линейного программирования характеризуется следующим образом.

Необходимо найти совокупность значений n переменных x₁, x₂, …, x_n, удовлетворяющих системе ограничений:

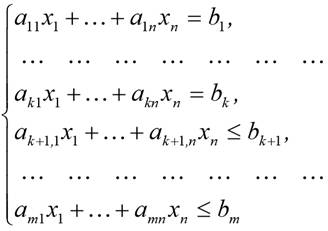
и условиям неотрицательности:

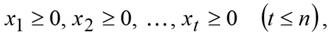
для которых целевая (линейная) функция:

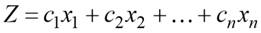
достигает экстремума (максимума или минимума).

Математическую модель данной задачи линейного программирования можно представить в следующем виде.

F(x₁, x₂, x₃) = x₁ * (3 + 2 * t) + x₂ * (7 - t) + x₃ * (6 - t) → max

 

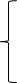
2 * x₁ + x₂ ≤ 620

2 * x₂ + x₃ ≤ 570

х₁ + x₂ ≤ 310

x₁, x₂, x₃ ≥ 0.

Методы решения.

Простой перебор. Возьмем некоторый многомерный параллелепипед, в котором лежит многогранник, задаваемый ограничениями. Как его построить? Например, если имеется ограничение типа 2 * x₁ + 5 * x₂ ≤ 10, то, очевидно, 0 ≤ x₁ ≤ 10 / 2 = 5 и 0 ≤ x₂ ≤ 10 / 2 = 5. Аналогичным образом от линейных ограничений общего вида можно перейти к ограничениям на отдельные переменные. Остается взять максимальные границы по каждой переменной. Если многогранник, задаваемый ограничениями, неограничен, то можно похожим, но несколько более сложным образом выделить его "обращенную" к началу координат часть, содержащую решение, и заключить ее в многомерный параллелепипед. Проведем перебор точек параллелепипеда с шагом 1 / 10ⁿ последовательно при n = 2, 3, …, вычисляя значения целевой функции и проверяя наличие ограничений. Из всех точек, удовлетворяющих ограничениям, возьмем ту, в которой целевая функция максимальна. Решение найдено. (Более строго выражаясь, найдено с точностью до 1 / 10ⁿ).  

Направленный перебор. Начнем с точки, удовлетворяющей ограничениям (ее можно найти простым перебором). Будем последовательно (или случайно – так называемый метод случайного поиска) менять ее координаты на определенную величину ∆, каждый раз в точку с более высоким значением целевой функции. Если выйдем на плоскость ограничения, будем двигаться по ней (находя одну из координат по уравнению ограничения). Затем движение по ребру (когда два ограничения-неравенства переходят в равенства). Остановка - в вершине линейного многогранника. Решение найдено. (Более строго выражаясь, найдено с точностью до ∆; если необходимо, в окрестности найденного решения проводим направленный перебор с шагом ∆ / 2 , ∆ / 4 и т.д.).

Симплекс-метод. Этот один из первых специализированных методов оптимизации, нацеленный на решение задач линейного программирования, в то время как методы простого и направленного перебора могут быть применены для  решения практически любой задачи оптимизации. Он был предложен американцем Г. Данцигом в 1951 г. Симплекс-метод состоит в продвижении по выпуклому многограннику ограничений от вершины к вершине, при котором на каждом шаге значение целевой функции улучшается до тех пор, пока не будет достигнут оптимум.

Геометрический метод. Если система ограничений задачи линейного программирования представлена в виде системы линейных неравенств с двумя переменными, то такая задача может быть решена геометрически. Таким образом, данный метод решения задачи линейного программирования имеет очень узкие рамки применения. Однако он представляет большой интерес с точки зрения выработки наглядных представлений о сущности задач линейного программирования. Геометрический (или графический) метод предполагает последовательное выполнение ряда шагов. Ниже представлен порядок решения задачи линейного программирования на основе ее геометрической интерпретации.

1. Сформулировать задачу линейного программирования.

2. Построить на плоскости {х₁, х₂} прямые, уравнения которых получаются в результате замены в ограничениях знаков неравенств на знаки точных равенств.

3. Найти полуплоскости, определяемые каждым из ограничений задачи.

4. Найти область допустимых решений.

5. Построить прямую c₁ * x₁ + c₂ * x₂ = h, где h - любое положительное число, желательно такое, чтобы проведенная прямая проходила через многоугольник решений.

6. Перемещать найденную прямую параллельно самой себе в направлении увеличения (при поиске максимума) или уменьшения (при поиске минимума) целевой функции. В результате, либо отыщется точка, в которой целевая функция принимает максимальное (минимальное) значение, либо будет установлена неограниченность функции на множестве решений.

7. Определить координаты точки максимума (минимума) функции и вычислить значение функции в этой точке.

Решение в MS Excel.

1.      Ячейки B2:B4 отведем под количество товара и заполним нулями.

2.      Ячейку D2, значение которой будем самостоятельно менять, отведем под время (t = 0, 1, 2, 4, 5).

3.      Ячейки F2:G4 отведем под ограничения (F2 =2*B2+B3, F3 = 2*B3+B4, F4 = B2+B3; G2 = 620, G3 = 570, G4 = 310).

4.      Ячейку J1 отведем под целевую функцию (J1 = B2*(3+2*D2)+B3*(7-D2)+B4*(6-D2)).

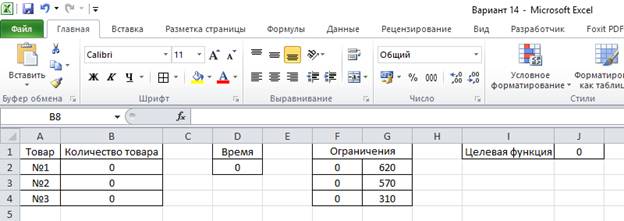
5.      Данные → Поиск решения.

6.      Выбираем параметры поиска решения следующим образом.

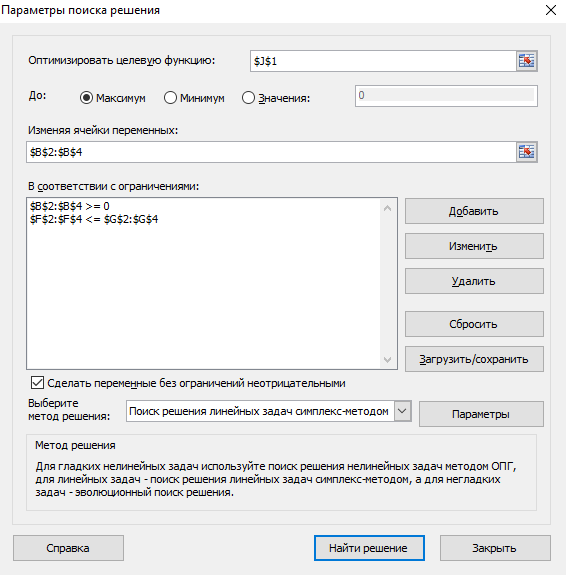
7.      Нажимаем на «Найти решение» и видим, что значения ячеек B2:B4 и J1 изменились.

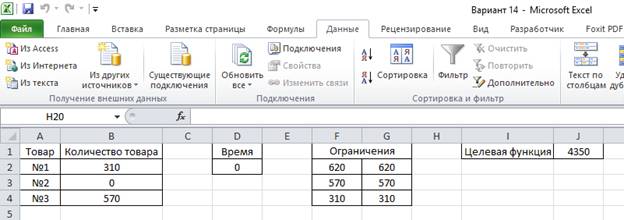
8.      Проделываем то же самое еще четыре раза, меняя при этом значение ячейки D2.

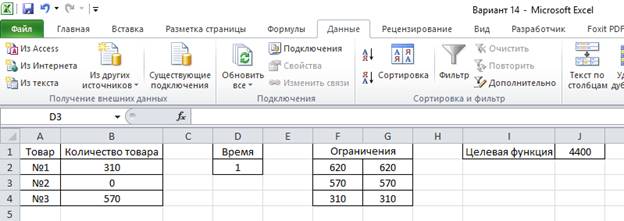
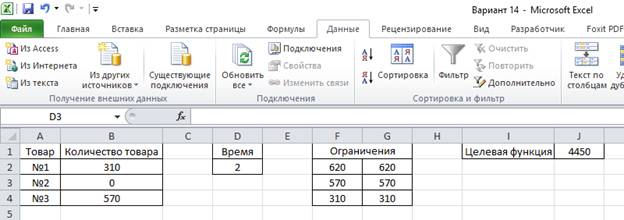
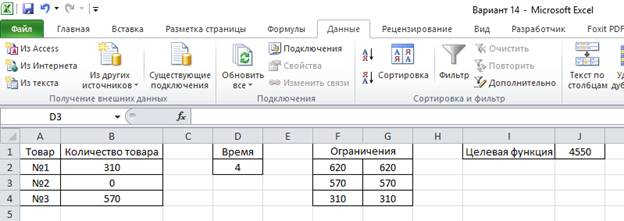
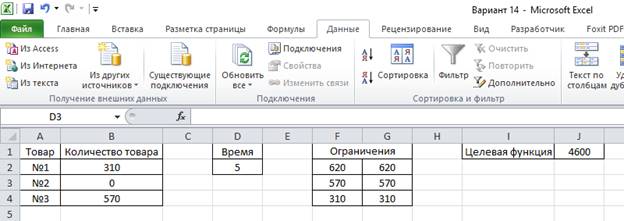
9.      Видим, что J1 = 4350 при D2 = 0, J1 = 4400 при D2 = 1, J1 = 4450 при D2 = 2, J1 = 4550 при D2 = 4, J1 = 4600 при D2 = 5.

10.   Из всех полученных значений выбираем наибольшее, т.е. 4600. Это и есть максимум стоимости всей партии товаров при изменении времени    t = 0, 1, 2 4, 5 и дополнительных ограничениях, задаваемых условиями хранения товаров.

Решение в Mathcad.

1.      Введем переменные x1 := 0, x2 := 0, x3 := 0, t = 0 и целевую функцию f(x1, x2, x3) := x1 * (3 + 2 * t) + x2 * (7 - t) + x3 * (6 - t).

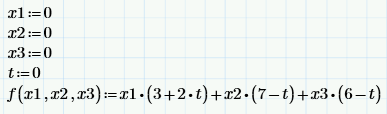
2.      Зададим блок решения с ограничениями (x1 ≥ 0, x2 ≥ 0, x3 ≥ 0, 2 * x1 + x2 £ 620, 2 * x2 + x3 £ 570, x1 + x2 £ 310) и операцией maximize для поиска значения переменных, при которых целевая функция достигает максимального значения.

3.      Видим, что полученные значения x1, x2, x3 совпадают со значениями в MS Excel.

4.      Найдем значение целевой функции при найденных x1, x2, x3, для этого обозначим как k транспонированную матрицу c и найдем f().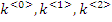

5.      Видим, что значение целевой функции равно 4600. Оно совпадает с полученным значением в MS Excel.

6.      Проделаем то же самое, но при этом меняя значение времени.

7.      Видим, что все полученные значения целевой функции совпадают со значениями в MS Excel. Наибольшим значением по-прежнему является 4600.

Решение в Mathematica.

1.      Составляем целевую функцию, задаем ограничения и указываем переменные (Maximize[{x1*(3+2*t)+x2*(7-t)+x3*(6-t),x1≥0,x2≥0,x3≥0,t==5,2*x1+x2≤620,2*x2+x3≤570,x1+x2≤310},{x1,x2,x3,t}]).

2.      Выбираем Evaluate Cell.

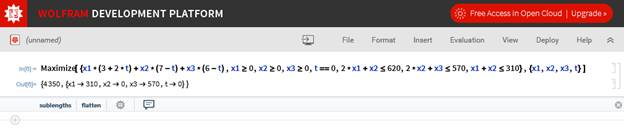
3.      Полученное значение целевой функции совпадает со значениями в Excel и Mathcad.

4.      Проделаем то же самое, но при этом меняя значение времени.

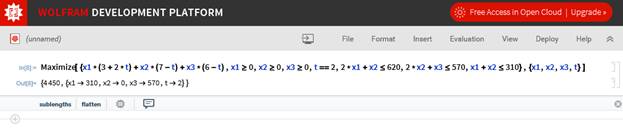
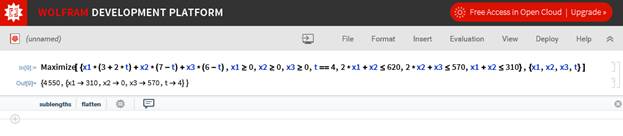
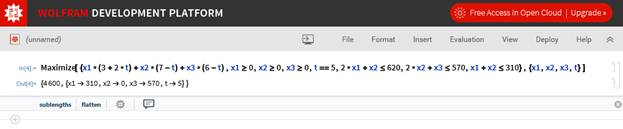
5.      Видим, что все полученные значения целевой функции совпадают со значениями в Mathcad и MS Excel. Наибольшим значением по-прежнему является 4600.

Анализ найденных решений.

Я решила задачу линейного программирования в пакетах трех математических программ: MS Excel, Mathcad и Mathematica. Полученные значения целевой функции совпадают во всех трех программах. Мне удалось выяснить, что максимальным значением стоимости всей партии товаров при изменении времени t = 0, 1, 2 4, 5 и дополнительных ограничениях, задаваемых условиями хранения товаров, является 4600. Этот максимум достигается при t = 5.

Как мне показалось, наиболее понятный для восприятия вид решения задачи линейного программирования у программы MS Excel благодаря ее наглядным таблицам и отсутствию сложных математических формул. Но при этом решение намного проще найти с помощью операции maximize в программе mathcad, хотя оно будет не в пару строк, что является возможным для программы mathematica.

Заключение.

Таким образом, я смогла убедиться на практике, что задачу оптимизации можно легко решить с помощью линейного программирования. Для этого достаточно лишь обладать одним из программных пакетов, используемых мною для данной курсовой работы.  

Список использованной литературы.

1.      А.И. Орлов. Основы теории принятия решений. Учебное пособие. Москва, 2002

2.      Акулич И.Л. «Математическое программирование в примерах и задачах», М. – Высшая школа, 1986

3.      Левина Н.С., Харджиева С.В., Цветкова А.Л. MS Excel и MS Project в решении экономических задач. – М.: Солон-Пресс, 2006 – 112 с.

4.      Л.С. Костевич. Математические программирование: Информ. Технологии оптимальных решений: Учеб. пособие. – Мн: Новое знание, 2003,- 424 с.