РЕСПУБЛИКА КАЗАХСТАН
АЛМАТИНСКИЙ ИНСТИТУТ ЭНЕРГЕТИКИ И СВЯЗИ
Кафедра Автоматической электросвязи
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
к курсовой работе
по дисциплине ТЦС
Тема
Проектирование тракта передачи данных между
источником и получателем информации
Выполнила:
М.К. Алибекова
Алматы 2007
ЗАДАНИЕ
Требуется спроектировать среднескоростной тракт передачи данных между двумя источниками и получателями, отстающими друг от друга на L км.
Для повышения верности передачи использовать систему с решающей обратной связью, непрерывной передачей и блокировкой приемника.
Тип кода циклический. Система с РОС работает в режиме обнаружения ошибок с переспросом неправильно принятой информации.
Распределение ошибок в дискретном канале описывается моделью Пуртова Л.П.. Для повышения надежности ТПД применяется постоянное время резервирования.
Требуется:
1) пояснить сущность модели частичного описания дискретного канала (модель Пуртова Л.П.), обратив особое внимание на параметр α - коэффициент группирования ошибок;
2) построить структурную схему системы с РОСнп и блокировкой и структурную схему алгоритма работы системы;
3) определить оптимальную длину кодовой комбинации n, при которой обеспечивается наибольшая относительная пропускная способность R;
4) определить число проверочных разрядов в кодовой комбинации r, обеспечивающих заданную вероятность необнаружения ошибки. Найти параметры циклического кода n, k, r;
5) выбрать тип образующего полинома g(x) с учетом последней цифры з.к.;
6) построить схему кодера для выбранного g(x) и пояснить его работу;
7) построить схему декодера для выбранного g(x) и пояснить его работу;
8) получить схему кодирующего и декодирующего устройства циклического кода с модуляцией и демодуляцией своего варианта, а также собрать схему с применением пакета «System View»;
9) определить объем передаваемой информации W при заданном темпе Tпер и критерии отказа tотк;
10) определить емкость накопителя М;
11) рассчитать надежностные показатели основного и обходного каналов;
12) по географической карте РК выбрать 2 пункта, отстоящих друг от друга на L км, выбрать магистраль, разбив ее на ряд участков длиной 500-1000 км. Пункты переприема привязать к крупным населенным пунктам;
13) построить временную диаграмму работы системы.
Исходные данные
B = 1200 – скорость модуляции
V = 80000 км/с – скорость распространения информации по каналу связи
Pош = 0,5 10-3 – вероятность ошибки в дискретном канале
Pно = 0,8 10-6- вероятность неопределения кодом ошибки
L = 4700 км – расстояние между источником и получателем
tотк = 60 сек – критерий отказа
Tпер = 580 сек – заданный темп
d0 = 6 – минимальное кодовое расстояние
α = 0,7 – коэффициент группирования ошибок
nФМ – тип модуляции
СОДЕРЖАНИЕ
ЗАДАНИЕ
ВВЕДЕНИЕ
ОСНОВНАЯ ЧАСТЬ
1 Модель частичного описания дискретного канала (модель Пуртова Л.П.)
2 Система передачи данных с РОС
2.1 Фазовая манипуляция
3 Оптимальная длина кодовой комбинации при использовании циклического кода в системе с РОС.
4 Параметры циклического кода
5 Расчет надежностных показателей основного и обходного каналов
6 Схемы кодера и декодера циклического кода
6.1 Кодирующее устройство циклического кода
6.2 Декодирующее устройство циклического кода
7 Количество передаваемой информации за время Т
8 Характеристики дискретного канала
8.1 Прямой ДК
8.2 Обратный ДК
9 Временная диаграмма работы системы
10 Магистраль на карте РК
ЗАКЛЮЧЕНИЕ
СПИСОК ЛИТЕРАТУРЫ
ПРИЛОЖЕНИЕ А
ПРИЛОЖЕНИЕ Б
ПРИЛОЖЕНИЕ В
ВВЕДЕНИЕ
Развитие телекоммуникационных сетей увеличивает роль и значение передачи дискретных сообщений в электросвязи.
Целью дисциплины ТЦС является:
· изложение принципов и методов передачи цифровых сигналов, научных основ и современное состояние технологии цифровой связи;
· дать представление о возможностях и естественных границах реализации цифровых систем передачи и обработки,
· уяснить закономерности, определяющие свойства устройств передачи данных и задачи их функционирования.
Основная задача - обучить теоретическим знаниям и алгоритмам построения систем ТДС, а также привить практические навыки по методологии инженерных расчетов основных характеристик и обучить методам технической эксплуатации цифровых систем и сетей.
Курсовой проект посвящен проектированию тракта передачи данных между источником информации и получателем информации. К качеству тракта передачи данных (ТПД) предъявляются очень высокие требования по верности передачи данных и надежности, поэтому проектируются некоммутируемой ТПД. Для повышения верности передачи использовать систему с решающей обратной связью, непрерывной передачей и блокировкой приемника. Тип кода – циклический.
Решение этих задач раскрывает выполнение основной цели задания – моделирование телекоммуникационных систем.
Кроме того, необходимо собрать схему с применением пакета «System View» для моделирования телекоммуникационных систем, кодирующего и декодирующего устройства циклического кода с использованием модуляции и демодуляции.
ОСНОВНАЯ ЧАСТЬ
среднескоростной тракт телекоммуникационная система
1. Модель частичного описания дискретного канала (модель Пуртова Л.П.)
По этой модели можно определить
зависимость вероятности появления искаженной комбинации от ее длины n и вероятности появления комбинации
длиной n с t ошибками.(t Зависимость вероятности
появления искаженной комбинации от ее длины n характеризуется как отношение числа искаженных кодовых
комбинаций Nош(n) общему числу переданных комбинаций N(n): P(>=1, n) = где вероятность P(>=1, n) – неубывающая функция n. При n=0, P(>=1, n) = Рош.
При n P(>=1, n)= где α – показатель группирования ошибок α = 0 – пакетирование ошибок
отсутствует, и появление ошибок следует считать независимым. α = 0,5 α = 0,3 α = 0,3 Распределение ошибок в
комбинациях различной длины оценивает не только вероятность появления
искаженных комбинаций (хотя бы 1 ошибка), но и вероятность комбинаций длиной n и t наперед заданными ошибками P(>= t, n): P(>= t, n)= Группирование ошибок
приводит к увеличению числа кодовых комбинаций, пораженных ошибками большой
кратности. При группировании ошибок
уменьшается число искаженных кодовых комбинаций заданной длины n. Примеры
зависимости Рисунок 1 -
Вероятности ошибки Эти зависимости,
снятые в реальных каналах связи и отмеченные на рисунке 1 точками, хорошо
аппроксимируются прямыми линиями при логарифмических масштабах. Для
определенной вероятности ошибок (Pош=0,002) пунктиром показаны две зависимости. Если бы ошибки не
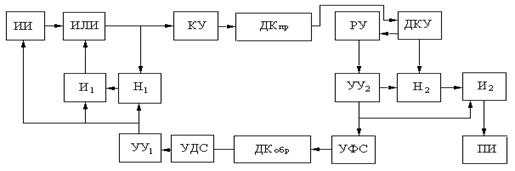
зависели друг от друга, то вероятность Рисунок 2 – Структурная схема системы с РОСнп
и блокировкой На
рисунке 2 представлена структурная схема системы с РОСнп
и блокировкой. Здесь: ИИ – источник информации; КУ – кодирующее устройство; ДК – прямой дискретный канал; РУ – решающее устройство; ДКУ – декодирующее устройство; УУ – устройство управления; УДС – устройство декодирования сигнала; УФС – устройство формирования сигнала; ПИ – получатель информации Передача информации осуществляется следующим образом.
При поступлении от источника информации ИИ кодовой комбинации происходят ее
кодирование помехоустойчивым кодом (в КУ) и запись в накопитель передачи Принятая
из прямого дискретного канала ( В
зависимости от результатов декодирования решающее устройство РУ принимает
решение о выдаче кодовой комбинации из накопителя приема через схему Блоки
управления приемником и передатчиком работают согласно структурной схеме
алгоритма, представленной на рисунке 3. Рисунок 3 – Структурная схема алгоритма
системы с РОСнп и блокировкой Фазовая манипуляция (phase shift keying - PSK)
была разработана в начале развития программы исследования дальнего космоса;
сейчас схема PSK широко используется в коммерческих и
военных системах связи. Фазо-манипулированный сигнал имеет следующий вид: Здесь фазовый член Аналитическое
представление:Сигнал: Вектор: Параметр Е – это энергия
символа, Т – время передачи символа, На практике фазовая
манипуляция используется при небольшом числе возможных значений начальной фазы
– как правило, 2, 4 или 8. Кроме того, при приеме сигнала сложно измерить
абсолютное значение начальной фазы; значительно проще определить относительный
фазовый сдвиг между двумя соседними символами. Поэтому обычно используется
фазоразностная манипуляция (синонимы – дифференциальная фазовая манипуляция,
относительная фазовая манипуляция; английский термин - differential phase shift keying , DPSK).
Длина
кодовой комбинации n должна быть
выбрана таким образом, чтобы обеспечить наибольшую пропускную способность
канала связи. При использовании корректирующего кода кодовая комбинация
содержит n разрядов, из которых k разрядов являются информационными, а
r разрядов – проверочными: n= k+r (3.1) Если в
системе связи используются двоичные сигналы (сигналы типа «1» и «0») и каждый
единичный элемент несет не более одного бита информации, то между скоростью
передачи информации и скоростью модуляции существует соотношение C = (k/n)*B, (3.2) где С –
скорость передачи информации, бит/с; В –
скорость модуляции, Бод. Очевидно,
что тем меньше r, тем больше
отношение k/n приближается к 1, тем меньше отличается С и В, т.е. тем выше
пропускная способность системы связи. Известно
также [3, стр. 104], что для циклических кодов с минимальным кодовым
расстоянием d0=3 справедливо соотношение Видно,
что чем больше n, тем ближе
отношение k/n к 1. Так, например, при n = 7, r=3, k=4, k/n = 0,571; при n = 255, r=8, k=247,
k/n = 0,964; n =
1023, r=10, k=1013, k/n = 0,990. Приведенное
утверждение справедливо для больших d0, хотя
точных соотношений для связей между r и n нет. Существуют только верхние и
нижние оценки, указанные на стр. 104 [3]. Из
изложенного можно сделать вывод, что с точки зрения внесения постоянной
избыточности в кодовую комбинацию выгодно выбирать длинные кодовые комбинации,
так как с увеличением n
относительная пропускная способность увеличивается, стремясь к пределу, равному
1. R= C/B= k/n (3.4) В
реальных каналах связи действуют помехи, приводящие к появлению ошибок в кодовых
комбинациях. При обнаружении ошибки декодирующим устройством в системах с РОС
производится переспрос группы кодовых комбинаций. Во время переспроса полезная
информации уменьшается. Можно
показать, что в этом случае где Р00
– вероятность обнаружения ошибки декодером (вероятность переспроса); РПП
– вероятность правильного приема (безошибочного приема) кодовой комбинации; М –
емкость накопителя передатчика в числе кодовых комбинаций. При
малых вероятностях ошибки в канале связи (Рош.< 10-3)
вероятность Р00 также мала, поэтому знаменатель мало отличается от 1
и можно считать При
независимых ошибках в канале связи, при тогда Емкость
накопителя [2, стр. 323] где tp – время распространения сигнала по
каналу связи, с; tk –
длительность кодовой комбинации из n разрядов, с. Знак
< > - означает, что при расчете М следует брать большее ближайшее целое
значение. Но где L – расстояние между оконечными
станциями, км; v – скорость
распространения сигнала по каналу связи, км/с; B – скорость
модуляции, Бод. После
простейших подстановок окончательно имеем Нетрудно
заметить, что при Рош = 0 формула (3.10) превращается в формулу (3.4). При
наличии ошибок в канале связи величина R является функцией Pош, n, k, B, L, v. Следовательно, существует оптимальное n (при заданных Pош, B, L, v), при котором относительная пропускная
способность будет максимальной. Формула
(3.10) еще более усложняется в случае зависимых ошибок в канале связи (при
пакетировании ошибок). Выведем
эту формулу для модели ошибок Пуртова. Как
показано в [1], число ошибок tоб в комбинации, длинной в n разрядов, определяется формулой 7.38
[1]. Для обнаружения такого числа ошибок находим циклический код с кодовым
расстоянием d0 не менее Как
показано [4], с некоторым приближением можно связать вероятность Подставляя
значение При
расчетах на микрокалькуляторах удобнее пользоваться десятичными логарифмами. После
преобразований Возвращаясь
к формулам (3.7) и (3.10) и производя замену k на n-r с учетом значения r, из формулы (3.13) получим Второй
член формулы (3.10) с учетом группирования ошибок по соотношению 7.37 [1]
примет вид Окончательно Примем n равной 31. Если при расчете
пропускная способность R
будет меньше 0.6, то рассчитаем ее для n равной 63. Итак, в моем случае: n = 31 R = 0.695 К
параметром циклического кода относятся: n – длина
кодовой комбинации (разрядов); k – длина
информационной части кодовой комбинации (разрядов); r – длина
проверочной части кодовой комбинации (разрядов); g (x) – вид образующего полинома циклического кода. После
определения оптимальной длины кодовой комбинации n, обеспечивающей наибольшую относительную пропускную
способность R, по формуле (3.13) определяют число
проверочных разрядов: Так как n , в моем случае, равно 31, то
воспользовавшись формулой (3.1), определим число информационных символов k: k = 31 – 10 = 21 Выбираем образующий
полином согласно последней цифре зачетной книжки и числу проверочных символов,
которые определяют степень g(x): g (x) = х10+х4+х3+х+1 Вероятность появления
ошибки известна (Рош=0,5∙10-3), полная вероятность
будет складываться из суммы следующих составляющих рпр – правильный
прием, рно – необнаружения ошибки, роб – вероятность
обнаружения ошибки декодером (вероятность переспроса). Зависимость вероятности
появления искаженной комбинации от ее длины характеризуется как отношение числа
искаженных кодовых комбинаций Nош(n) к общему числу переданных комбинаций N(n): Вероятность Р(≥1,n) является не убывающей функцией n. При n=1 Р(≥1,n)=рош,
а при n→∞ вероятность Р(≥1,n) →1. Вероятность
необнаруживаемой кодом ошибки определяется по формуле: В моем случае она равна
1,368*10-6. Вероятность
обнаруживаемой кодом ошибки: Подставив числовые
значения, получим 1,4*10-3. Вероятность правильного
прием: В данном случае она равна
0,999,то есть близка к единице. Избыточность кода: Подставим параметры
циклического кода и получим Скорость кода: Подставим в данную
формулу вычисленное ранее значение избыточности кода и получим скорость кода
равную 0,667. Избыточность необходимая
для обеспечения в ДК вероятности необнаружения кодом ошибки определяется по
формуле: где Rнпбл – средняя относительная скорость
передачи в РОСнп и блокировкой где Итак, избыточность
необходимая для обеспечения в ДК вероятности необнаружения кодом ошибки будет
равна 0,33. Рассмотрим построение и
принцип действия кодера и декодера циклического (31,21) кода. Выбираем
образующий: g (x) = х10+х4+х3+х+1 Работа
кодера на его выходе характеризуется следующим: 1.Формирование k элементов информационной группы и
одновременно деление полинома, отображающего информационную часть хr m(х), на порождающий (образующий ) полином
g(х) с целью получения остатка от деления r(х). 2. Формирование проверочных r элементов путем считывания их с ячеек
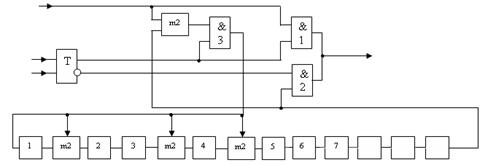
схемы деления хr m(х) на выход кодера. Структурная схема кодера
приведена на рисунке 4. Цикл работы кодера для
передачи n = 31 единичных элементов составляет n тактов. Тактовые сигналы формируются
передающим распределителем, который на схеме не указан . Первый режим работы
кодера длится k = 21 тактов. От первого тактового
импульса триггер Т занимает положение, при котором на его прямом выходе
появляется сигнал "1", а на инверсном - сигнал "0". Сигналом
"1" открываются ключи (логические схемы И) 1 и 3 . Сигналом
"0" ключ 2 закрыт. В таком состоянии триггер и ключи
находятся k+1 тактов, т.е. 22 тактов. За это время на
выход кодера через открытый ключ 1 поступят 56 единичных элементов
информационной группы k =21. Одновременно через
открытый ключ 3 информационные элементы поступают на устройство деления
многочлена хr m(х) на g(х). Деление осуществляется
многотактным фильтром с числом ячеек, равным числу проверочных разрядов (степени
порождающего полинома). В рассматриваемом случае число ячеек г=10. Число
сумматоров в устройстве равно числу ненулевых членов g(х) минус
единица. В нашем случае число
сумматоров равно четырем. Сумматоры устанавливаются после ячеек,
соответствующих ненулевым членам g(х). Поскольку все неприводимые полиномы
имеют член х°=1, то соответствующий этому члену сумматор установлен
перед ключом 3 (логической схемой И). После k=21 тактов в
ячейках устройства деления окажется записанным остаток от деления г(х). При воздействии k+1= 22 тактового импульса триггер Т изменяет свое состояние: на инверсном
выходе появляется сигнал "1", а на прямом - "0". Ключи 1 и
3 закрываются, а ключ 2 открывается. За оставшиеся r=10 тактов элементы остатка от деления (проверочная группа) через ключ 2 поступают
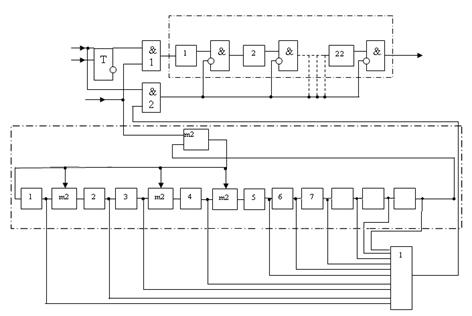
на выход кодера, также начиная со старшего разряда. Рисунок 4 - Структурная схема кодера Рисунок 5 - Структурная схема декодера Функционирование схемы
декодера (рисунок 5) сводится к следующему. Принятая кодовая комбинация,
которая отображается полиномом Р(х) поступает в декодирующий регистр и
одновременно в ячейки буферного регистра, который содержит k ячеек. Ячейки буферного регистра
связаны через логические схемы "нет", пропускающие сигналы только при
наличии "1" на первом входе и "0" - на втором (этот вход
отмечен кружочком). На вход буферного регистра кодовая комбинация поступит
через схему И1. Этот ключ открывается с выхода триггера Т первым
тактовым импульсом и закрывается k+1 тактовым импульсом (полностью
аналогично работе триггера Т в схеме кодера) . Таким образом, после k тактов информационная группа
элементов будет записана в буферный регистр. Схемы НЕТ в режиме заполнения
регистра открыты, ибо на вторые входы напряжение со стороны ключа И2
не поступает. Одновременно в декодирующем
регистре происходит в продолжение всех n=31 тактов деление кодовой комбинации (полином Р(х)
на порождающий полином g(х)). Схема декодирующего регистра полностью аналогична схеме
деления кодера, которая подробно рассматривалась выше. Если в результате деления
получится нулевой остаток - синдром S(х)=0, то последующие тактовые импульсы спишут информационные элементы
на выход декодера. При наличии ошибок в
принятой комбинации синдром S(х) не равен 0. Это означает, что
после n - го (31) такта хотя бы в одной ячейке декодирующего
регистра будет записана “1”. Тогда на выходе схемы ИЛИ появится сигнал.
Ключ 2 (схема И2) сработает, схемы НЕТ буферного регистра
закроются, а очередной тактовый импульс переведет все ячейки регистра в
состояние "0". Неправильно принятая информация будет стерта.
Одновременно сигнал стирания используется как команда на блокировку
приемника и переспрос. Пусть требуется
передавать информацию за временной интервал Т который называется темпом
передачи информации Критерий отказа tотк - это суммарная длительность всех
неисправностей, которая допустима за время Т. Если время неисправностей
за промежуток времени Т превысит tотк, то система передачи данных будет находиться в состоянии
отказа, С учетом выбранных
параметров кода W
= R*B*(Tпер
– tотк), (7.1) где
R - наибольшая
относительная пропускная способность для выбранных параметров циклического
кода. W
= 0,695∙1200∙(580-60)=433680 бит Максимальная скорость
работы по каналу равна скорости модуляции В = 1200 Бод. Распределение
вероятности возникновения хотя бы одной ошибки на длине n определяется по формуле (1.2) P(>=1, n) = Распределение вероятности
возникновения ошибки кратности t и
более на длине n определяется по
формуле (1.3) для она равна P(>= t, n) = для P(>= t, n) = Время распределения
определим по формуле (3.9): Максимальная скорость
работы по каналу равна скорости модуляции В = 200 Бод. Распределение вероятности
возникновения хотя бы одной ошибки на длине n и распределение вероятности возникновения ошибки кратности t и более на длине n такие как в прямом ДК. Емкость накопителя М
определяется по формуле (3.8) где tp – время распространения сигнала по
каналу связи, с; tk –
длительность кодовой комбинации из n разрядов, с. Время
распространения сигнала по каналу связи и длительность кодовой комбинации из n разрядов определим по формулам (3.9): где L – расстояние между оконечными
станциями, км; v – скорость
распространения сигнала по каналу связи, км/с; B – скорость
модуляции, Бод. Будем
считать, что tс = tк
= 0,02583 сек tа.к.= tа.с.= 0.5 tк = 0,012915 сек Для правильного
построения диаграммы совершенно необходимо соблюдать временной масштаб и
учитывать соотношение между величинами tс , tк , tа.к., tа.с., tр. tож= tp"+ tр^^+ tак+ tас+ tc, (8.1) где tp" – время распределения по прямому ДК tр^^ - время распределения по обратному ДК tак – время анализа канала tас - время анализа сигнала Таким образом, tож =2*0,05875+2*0,012915+0,02583=
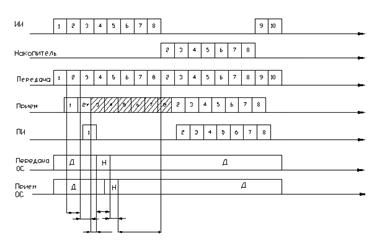
0,16916 сек Временная диаграмма
(рисунок 6) иллюстрирует работу системы с РОСНП и блокировкой при обнаружении
ошибки во второй комбинации в случае с h=8. Как видно из диаграммы, передача комбинации ИИ
осуществляется непрерывно до момента получения передатчиком сигнала переспроса.
После этого передача информации от ИИ прекращается на время tож и 8 комбинаций начиная со второй. В
это время в приемнике стираются h
комбинаций: вторая комбинация, в которой обнаружена ошибка (отмечена
звездочкой) и 6 последующих комбинаций (заштрихованы). Получив переданные из
накопителя комбинации (от второй до 8-ой включительно) приемник выдает их ПИ, а
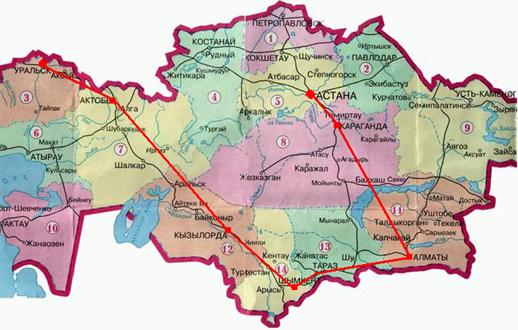
передатчик продолжает передачу последующих комбинаций. Рисунок 6 – Временная диаграмма работы системы Уральск - 0 км; Актюбинск - 1004,5 км; Кызылорда - 1893,5 км; Шымкент – 2100 км; Тараз - 2453,5 км; Алматы - 3500,5 км; Караганда – 4020,5 км; Астана - 4700 км. Рисунок 7 – Выбор магистрали по карте РК В ходе
выполнения данной курсовой работы я ·
пояснила сущность
модели частичного описания дискретного канала (модель Пуртова Л.П.); ·
построила
структурную схему системы с РОСнп и блокировкой и структурную схему
алгоритма работы системы; ·
определила
оптимальную длину кодовой комбинации n, при которой обеспечивается наибольшая относительная пропускная
способность R, а также число проверочных разрядов
в кодовой комбинации r,
обеспечивающих заданную вероятность необнаружения ошибки; ·
нашла параметры
циклического кода n, k, r; ·
выбрала тип
образующего полинома g(x) с учетом последней цифры з.к.; ·
построила схему
кодера и декодера для выбранного g(x) и пояснила их работу; ·
получила схему
кодирующего и декодирующего устройства циклического кода своего варианта, а
также собрала схему с применением пакета «System View»; ·
определила объем
передаваемой информации W при
заданном темпе Tпер и критерии отказа tотк, емкость накопителя М; ·
рассчитала
надежностные показатели основного и обходного каналов; ·
построила
временную диаграмму работы системы. В результате мной была
выполнена основная задача курсовой работы – моделирование телекоммуникационных
систем. 1.
Скляр Б. Цифровая
связь. Теоретические основы и практическое применение: 2-е изд. /Пер. с англ.- М.: Издательский дом «Вильямс»,
2003. - 1104 с. 2.
Прокис Дж.
Цифровая связь. Радио и связь, 2000.-797с. 3.
А.Б. Сергиенко.
Цифровая обработка сигналов: Учебник для вузов. - М.:-2002. 4.
Фирменный
стандарт. Работы учебные. Общие требования к построению, изложению, оформлению
и содержанию. ФС РК 10352-1910-У-е-001-2002. – Алматы: АИЭС, 2002. 5.
1 Шварцман В.О.,
Емельянов Г.А. Теория передачи дискретной информации. – М.: Связь, 1979. -424
с. 6.
Передача дискретных
сообщений / Под ред. В.П. Шувалова. - М.: Радио и связь, 1990. -464 с. 7.
Емельянов Г.А.,
Шварцман В.О. Передача дискретной информации. - М.: Радио и связь, 1982. - 240
с. 8.
Пуртов Л.П. и др.
Элементы теории передачи дискретной информации. – М.: Связь, 1972. – 232 с. 9.
Колесник В.Д.,
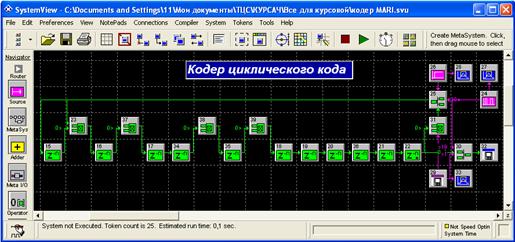
Мирончиков Е.Т.. Декодирование циклических кодов.- М.: Связь, 1968. Кодер циклического
кода Рисунок А.1 – Схема кодера циклического кода,
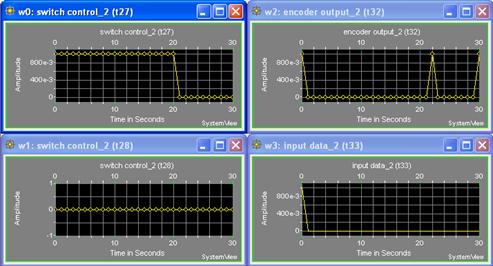
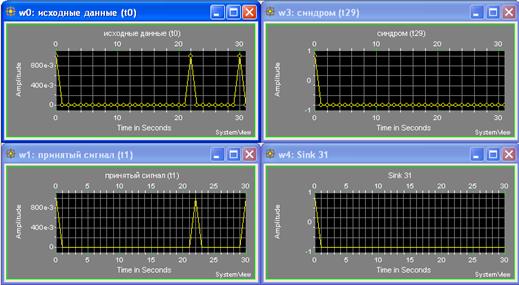
выполненная с применением пакета «System View» Рисунок А.2 – Входные и выходные сигналы кодера
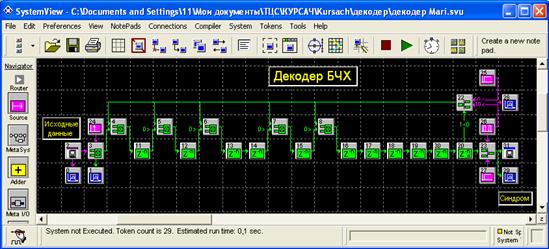
циклического кода Декодер циклического
кода Рисунок Б.1 – Схема декодера циклического кода,
выполненная с применением пакета «System View» Рисунок Б.2 – Входные и выходные сигналы декодера
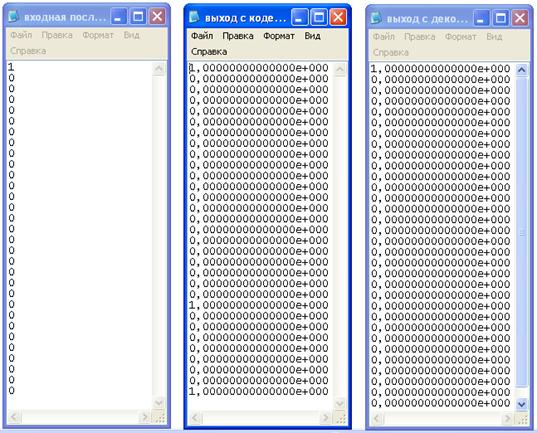
циклического кода Рисунок В.1 – Входные и выходные последовательности
для кодера и декодера циклического кода Размещено на http://www.![]() , (1.1)
, (1.1)![]() , P(>=1, n)
, P(>=1, n) ![]() 1
1![]() , (1.2)
, (1.2)![]() 0,7 – наблюдается на кабельных
линиях связи, т.к. кратковременные прерывания приводят к появлению групп с
большой плотностью ошибок.
0,7 – наблюдается на кабельных
линиях связи, т.к. кратковременные прерывания приводят к появлению групп с
большой плотностью ошибок.![]() 0,5 – пакетирование в
радиорелейных линиях связи с интервалами большой плотности ошибок; имеется
интервалы с редкими ошибками.
0,5 – пакетирование в
радиорелейных линиях связи с интервалами большой плотности ошибок; имеется
интервалы с редкими ошибками.![]() 0,4 – в радиотелеграфных каналах.
0,4 – в радиотелеграфных каналах.![]() (1.3)
(1.3)![]() от длины блока n показаны на рисунке 1.
от длины блока n показаны на рисунке 1. 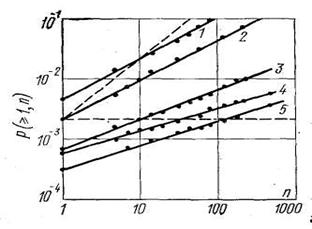
![]() в зависимости от длины n: 1 – КВ радиотелеграфный канал; 2 –
коммутируемый канал ТЧ кабельной линии; 3 – канал ТЧ радиорелейной линии; 4 –
телеграфный канал кабельной линии; 5 – некоммутируемый канал ТЧ кабельной
линии.
в зависимости от длины n: 1 – КВ радиотелеграфный канал; 2 –
коммутируемый канал ТЧ кабельной линии; 3 – канал ТЧ радиорелейной линии; 4 –
телеграфный канал кабельной линии; 5 – некоммутируемый канал ТЧ кабельной
линии.![]() не зависела бы от n и шла под углом 45˚. Если бы
ошибки были сгруппированы подряд в одну группу, то
не зависела бы от n и шла под углом 45˚. Если бы
ошибки были сгруппированы подряд в одну группу, то ![]() не зависела бы от длины кодовой
комбинации n и была бы параллельна оси абсцисс.
Из рисунка 1 видно, что характеристика реального канала (прямая 2) лежит между
этими двумя предельными характеристиками.
не зависела бы от длины кодовой
комбинации n и была бы параллельна оси абсцисс.
Из рисунка 1 видно, что характеристика реального канала (прямая 2) лежит между
этими двумя предельными характеристиками.
2 Система передачи данных с РОС
![]() . Закодированная информация передается по прямому
дискретному каналу.
. Закодированная информация передается по прямому
дискретному каналу. ![]() ) кодовая комбинация кодируется (в ДКУ) и записывается
в накопитель приема
) кодовая комбинация кодируется (в ДКУ) и записывается
в накопитель приема ![]() . Комбинация может быть декодирована
правильно, то есть соответствовать переданной кодовой комбинации; она может
содержать необнаруженную ошибку в результате перехода переданной кодовой
комбинации в другую разрешенную кодовую комбинацию; наконец, в результате
декодирования может быть обнаружена ошибка (если переданная кодовая комбинация
перешла в неразрешенную). Вероятность наступления каждого из трех указанных
событий зависит от характеристик дискретного канала, помехоустойчивого кода и
метода декодирования.
. Комбинация может быть декодирована
правильно, то есть соответствовать переданной кодовой комбинации; она может
содержать необнаруженную ошибку в результате перехода переданной кодовой
комбинации в другую разрешенную кодовую комбинацию; наконец, в результате
декодирования может быть обнаружена ошибка (если переданная кодовая комбинация
перешла в неразрешенную). Вероятность наступления каждого из трех указанных
событий зависит от характеристик дискретного канала, помехоустойчивого кода и
метода декодирования.![]() потребителю или о ее стирании в накопителе. Первое из
этих решений принимается в случае отсутствия ошибок или при необнаруженных
ошибках, а второе – при обнаружении ошибок. В первом случае одновременно с
выдачей кодовой комбинации получателю информации ПИ устройством управления
потребителю или о ее стирании в накопителе. Первое из
этих решений принимается в случае отсутствия ошибок или при необнаруженных
ошибках, а второе – при обнаружении ошибок. В первом случае одновременно с
выдачей кодовой комбинации получателю информации ПИ устройством управления ![]() и устройством УФС формирования сигнала ОС формируется
сигнал подтверждения, который по обратному дискретному каналу (
и устройством УФС формирования сигнала ОС формируется
сигнал подтверждения, который по обратному дискретному каналу (![]() ) передается в передатчик. После получения сигнала
подтверждения и его декодировании в УДС,
) передается в передатчик. После получения сигнала
подтверждения и его декодировании в УДС, ![]() передатчика запрашивает у источника информации
следующую кодовую комбинацию и описанный выше цикл работы повторяется. Схема
передатчика запрашивает у источника информации
следующую кодовую комбинацию и описанный выше цикл работы повторяется. Схема ![]() при этом закрыта, поэтому при поступлении новой
кодовой комбинации ранее переданная комбинация в накопителе передачи стирается.
Во втором случае одновременно с решением о стирании в УФС формируется сигнал
переспроса, который по обратному дискретному каналу передается в передатчик.
После получения и декодирования сигнала переспроса из накопителя передачи через
схему ИЛИ повторно передается та же кодовая комбинация.
при этом закрыта, поэтому при поступлении новой
кодовой комбинации ранее переданная комбинация в накопителе передачи стирается.
Во втором случае одновременно с решением о стирании в УФС формируется сигнал
переспроса, который по обратному дискретному каналу передается в передатчик.
После получения и декодирования сигнала переспроса из накопителя передачи через
схему ИЛИ повторно передается та же кодовая комбинация. 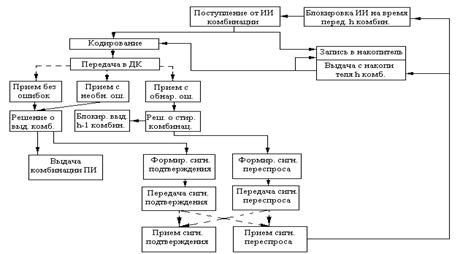
2.1 Фазовая манипуляция
![]()
![]()
![]()
![]() может
принимать М дискретных значений, обычно определяемых следующим образом:
может
принимать М дискретных значений, обычно определяемых следующим образом:![]()
![]()
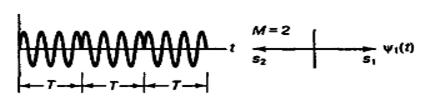
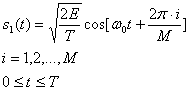
![]() . Работа схемы модуляции
заключается в смещении фазы модулируемого сигнала s1(t) на одно из двух
значений, нуль или π (180º). Типичный вид BPSK-модулированного сигнала приведен на рис., где явно
видны характерные резкие изменения фазы при переходе между символами; если
модулируемый поток данных состоит из чередующихся нулей и единиц, такие резкие
изменения будут происходить при каждом переходе. Модулированный сигнал можно
представить как вектор на графике в полярной системе координат; длина вектора
соответствует амплитуде сигнала, а его ориентация в общем М-арном случае – фаза
сигнала относительно других М-1 сигналов набора. При модуляции BPSK векторное представление дает два
противофазных(180º) вектора. Наборы сигналов, которые могут быть
представлены подобными противофазными векторами, называются антиподными.
. Работа схемы модуляции
заключается в смещении фазы модулируемого сигнала s1(t) на одно из двух
значений, нуль или π (180º). Типичный вид BPSK-модулированного сигнала приведен на рис., где явно
видны характерные резкие изменения фазы при переходе между символами; если
модулируемый поток данных состоит из чередующихся нулей и единиц, такие резкие
изменения будут происходить при каждом переходе. Модулированный сигнал можно
представить как вектор на графике в полярной системе координат; длина вектора
соответствует амплитуде сигнала, а его ориентация в общем М-арном случае – фаза
сигнала относительно других М-1 сигналов набора. При модуляции BPSK векторное представление дает два
противофазных(180º) вектора. Наборы сигналов, которые могут быть
представлены подобными противофазными векторами, называются антиподными.
3 Оптимальная длина кодовой комбинации
при использовании циклического кода в системе с РОС
![]() (3.3)
(3.3)![]() , (3.5)
, (3.5)![]() (3.6)
(3.6)![]()
![]() ,
,![]() (3.7)
(3.7)![]() , (3.8)
, (3.8)![]() , (3.9)
, (3.9)![]() (3.10)
(3.10)![]() . Поэтому, согласно формуле 7.38
[1], необходимо определить вероятность
. Поэтому, согласно формуле 7.38
[1], необходимо определить вероятность![]()
![]() с вероятностью не
обнаружения декодером ошибки РНО и числом проверочных разрядов в
кодовой комбинации
с вероятностью не
обнаружения декодером ошибки РНО и числом проверочных разрядов в
кодовой комбинации![]() (3.11)
(3.11)![]() в
(9) с заменой tоб на d0-1, имеем
в
(9) с заменой tоб на d0-1, имеем![]() (3.12)
(3.12)![]() (3.13)
(3.13)![]()
![]()
![]() (3.14)
(3.14)![]()
4. Параметры циклического кода
![]()
5. Расчет надежностных показателей
основного и обходного каналов
![]() (5.1)
(5.1)![]() (5.2)
(5.2)![]() (5.3)
(5.3)
![]() (5.4)
(5.4)![]() (5.5)
(5.5)![]() =0,323.
=0,323.![]() (5.6)
(5.6)![]() , (5.7)
, (5.7)![]() (5.8)
(5.8)![]()
![]()
6. Схемы кодера и декодера циклического
кода
6.1 Кодирующее устройство циклического
кода
6.2 Декодирующее устройство
циклического кода
7. Количество передаваемой информации
за время Т
8. Характеристики дискретного канала
8.1 Прямой ДК
![]() = 1,401*10-3
= 1,401*10-3![]()
![]() = 6,823*10-4
= 6,823*10-4![]()
![]() = 8,643*10-4
= 8,643*10-4![]()
8.2 Обратный ДК
9. Временная диаграмма работы системы
![]() = 8,
= 8, ![]() ,
, 
10. Магистраль на карте РК
ПРИЛОЖЕНИЕ А
ПРИЛОЖЕНИЕ Б
ПРИЛОЖЕНИЕ В














 (zip - application/zip)
(zip - application/zip)










