Основы теории кодирования. Теоремы о кодах

Федеральная таможенная служба
Государственное казенное образовательное учреждение
высшего образования
«Российская таможенная академия»
Владивостокский филиал
_____________________________________________________________
Кафедра информатики и информационных таможенных технологий

Реферат
по дисциплине «Информатика»
на тему: «Основы теории кодирования. Теоремы о кодах»

Выполнил студент ФТД
Учебной группы Тс02/1501
Подлесная Дарья
Подпись ____________________

Проверил____________________
Подпись ____________________

Владивосток

2016

Оглавление

Введение4

Глава 1. История кодирования 5

Глава 2.Теория кодирования 6-7

2.1.Основные задачи и определения в теории кодирования 6-7

2.2Основные теоремы о кодах8

Глава 3.Практика кодирования9

3.1 Кодирование сигнала………………………………………………………………...…..…..9

Заключение………………………………………………………………………………......….10

Список использованной литературы………………………………………………………….11

Введение

Коды возникли в глубокой древности,  фактически с появлением системы знаков для записи звуков, слов, и информации, которые позднее развились в различные языки. Каждый язык представляет собой сложную систему кодирования, включая в свою конструкцию алфавит, слова, грамматику. Язык позволяет передавать в окружающем шуме информацию быстро, надежно и с достаточной степенью избыточности. В течении многих веков люди занимались засекречиванием информации и созданием кодов. Впоследствии была разработана теория кодирования, являющаяся одним из разделов теоретической информатики. Быстрый рост объемов обработки данных, развитие вычислительных сетей предъявляют высокие требования к минимизации ошибок в используемой информации. Переход всех видов создания, хранения, использования и передачи данных, а также средств вещания на цифровые методы, происходящий сейчас во всём мире, ещё более повышает важность высококачественной передачи цифровых потоков. Успешная работа этих систем возможна только при наличии специальной эффективной аппаратуры, которая позволяет гарантировать достоверную передачу информации. Важнейший вклад в повышение достоверности обмена цифровыми данными вносит теория кодирования.

В настоящее время теория кодирования имеет широкое практическое применение как средство экономной, быстрой, а также надежной передачи информации по линиям связи, предполагая отсутствие потерь информации. Иными словами, данная теория изучает, как лучше упаковать данные, чтобы после передачи сигнала из данных можно было надежно и просто выделить полезную информацию. Иногда теорию кодирования путают с шифрованием, но это неверно: криптография решает обратную задачу, ее цель — затруднить получение информации из данных.

 Глава 1. История кодирования

Необходимость кодирования информации возникла задолго до появления компьютеров. Речь, азбука и цифры – есть не что иное, как система моделирования мыслей, речевых звуков и числовой информации. В технике потребность кодирования возникла сразу после создания телеграфа, но особенно важной она стала с изобретением компьютеров. С необходимостью кодирования данных впервые столкнулись более полутораста лет назад, вскоре после изобретения телеграфа. Каналы были дороги и ненадежны, что сделало актуальной задачу минимизации стоимости и повышения надёжности передачи телеграмм. Проблема ещё более обострилась в связи с прокладкой трансатлантических кабелей. С 1845 вошли в употребление специальные кодовые книги; с их помощью телеграфисты вручную выполняли «компрессию» сообщений, заменяя распространенные последовательности слов более короткими кодами. Тогда же для проверки правильности передачи стали использовать контроль чётности, метод, который применялся для проверки правильности ввода перфокарт ещё и в компьютерах первых поколений. Для этого во вводимую колоду последней вкладывали специально подготовленную карту с контрольной суммой. Если устройство ввода было не слишком надежным (или колода – слишком большой), то могла возникнуть ошибка. Чтобы исправить её, процедуру ввода повторяли до тех пор, пока подсчитанная контрольная сумма не совпадала с суммой, сохраненной на карте. Эта схема неудобна, и к тому же пропускает двойные ошибки. С развитием каналов связи потребовался более эффективный механизм контроля.

 Первым теоретическое решение проблемы передачи данных по зашумленным каналам предложил Клод Шеннон, основоположник статистической теории информации. Работая в Bell Labs, Шеннон написал работу «Математическая теория передачи сообщений» (1948), где показал, что если пропускная способность канала выше энтропии источника сообщений, то сообщение можно закодировать так, что оно будет передано без излишних задержек[1]. В одной из теорем Шеннон доказал, что при наличии канала с достаточной пропускной способностью сообщение может быть передано с некоторыми временными задержками. Кроме того, он показал возможность достоверной передачи при наличии шума в канале. Труды Шеннона дали пищу для множества дальнейших исследований в области теории информации, но практического инженерного приложения они не имели. Переход от теории к практике стал возможен благодаря усилиям Ричарда Хэмминга, коллеги Шеннона по Bell Labs, получившего известность за открытие класса кодов «коды Хэмминга». Существует легенда, что к изобретению своих кодов Хэмминга подтолкнуло неудобство в работе с перфокартами на релейной счетной машине Bell Model V в середине 40-х годов. Ему давали время для работы на машине в выходные дни, когда не было операторов, и ему самому приходилось возиться с вводом. Хэмминг предложил коды, способные корректировать ошибки в каналах связи, в том числе и в магистралях передачи данных в компьютерах, прежде всего между процессором и памятью. Коды Хэмминга показали, как можно практически реализовать возможности теоремы Шеннона. Хэмминг опубликовал свою статью в 1950, хотя во внутренних отчетах его теория кодирования датируется 1947. Поэтому некоторые считают, что отцом теории кодирования следует считать Хэмминга, а не Шеннона[2].

Глава 2.Теория кодирования

2.1 Основные задачи и определения

Теория кодирования информации является одним из разделов теоретической информатики. К основным задачам, решаемым в данном разделе, необходимо отнести следующие: разработка принципов наиболее экономичного кодирования информации; согласование параметров передаваемой информации с особенностями канала связи; разработка приемов, обеспечивающих надежность передачи информации по каналам связи, т.е. отсутствие потерь информации[3]. Две последние задачи связаны с процессами передачи информации. Первая же задача – кодирование информации – касается не только передачи, но и обработки, и хранения информации, т.е. охватывает широкий круг проблем; частным их решением будет представление информации в компьютере.

Кодирование информации - процесс преобразования сигнала из формы, удобной для непосредственного использования информации, в форму, удобную для передачи, хранения или автоматической переработки. Говоря строже, это правило, описывающее отображение одного набора знаков в другой набор знаков. Процесс преобразования сообщения в комбинацию символов в соответствии с кодом называется кодированием, а процесс восстановления сообщения из комбинации символов называется декодированием. Подобные преобразования сообщения осуществляются в момент поступления сообщения от источника в канал связи (кодирование) и в момент приема сообщения получателем (декодирование). Устройства, обеспечивающие кодирование и декодирование, соответственно называют кодировщиком и декодировщиком[4].

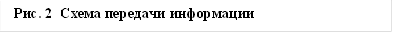
Операции кодирования и декодирования называются обратимыми, если их последовательное применение обеспечивает возврат к исходной информации без каких-либо её потерь. Примером обратимого кодирования является представление знаков в телеграфном коде и их восстановление после передачи. Примером кодирования необратимого может служить перевод с одного естественного языка на другой – обратный перевод, вообще говоря, не восстанавливает исходного текста. Кодер – программа (или устройство), реализующая определенный алгоритм кодирования данных (например, архиватор, или кодер MP 3), который в качестве ввода принимает исходную информацию, а в качестве вывода возвращает закодированную информацию в определенном формате. Декодер – программа (или устройство), реализующая обратное преобразование закодированного сигнала в декодированный. Кодек (от англ. « codec » - « Coder/ Decoder») - программный или аппаратный блок, предназначенный для кодирования/декодирования данных.(Пример: MPC – MusePack).

 Для представления дискретной информации используется некоторый алфавит. Однако однозначное соответствие между информацией и алфавитом отсутствует. Другими словами, одна и та же информация может быть представлена посредством различных алфавитов. В связи с такой возможностью возникает проблема перехода от одного алфавита к другому, причём, такое преобразование не должно приводить к потере информации. Алфавит, с помощью которого представляется информация до преобразования называется первичным; алфавит конечного представления – вторичным. В теории кодирования также выделяют понятие кода – совокупности знаков (символов) и системы определённых правил, при помощи которой информация может быть представлена (закодирована) в виде набора  символов для передачи, обработки и хранения информации[5]. Конечная последовательность кодовых знаков называется символом. Код – набор символов, которому приписан некоторый смысл. Любой код должен обеспечивать однозначное чтение сообщения (надежность), так и, желательно, быть экономным (использовать в среднем поменьше символов на сообщение). Экономное сообщение может повысить скорость обработки, но может и уменьшить ее. Например, очень экономно использовать вместо фамилий и имен учеников школы коды типа 10А5 (десятый класс «А», пятый по порядку в журнале). Но тогда надо либо помнить все соответствия между фамилиями и кодами, либо каждый раз обращаться к журналу. Повысить качество всех параметров одновременно нельзя: улучшение одного из них, как правило, ухудшает другой. Выход из положения нашли в том, что на разных этапах передачи информации совершенствуют разные параметры, т. е. в процессе передачи информацию несколько раз перекодируют, причём с разными целями. Например, текст телеграммы, написанный на обычном языке, преобразуют в один из телеграфных кодов, который технически удобнее передавать, а при приёме снова превращают в обычный текст. Но иногда выбирают наиболее важный параметр и улучшают в первую очередь его.  

Кодирование предшествует передаче и хранению информации. При этом хранение связано с фиксацией некоторого состояния носителя информации, а передача – с изменением состояния с течением времени (т.е. процессом). Эти состояния или сигналы будем называть элементарными сигналами – именно их совокупность и составляет вторичный алфавит.

Возможность восстановить текст означает, что в языке имеется определенная избыточность, за счет которой мы восстанавливаем отсутствующие элементы по оставшимся. Ясно, что избыточность находится в вероятностях букв и их комбинациях, их знание позволяет подобрать наиболее вероятный ответ. Компьютер может обрабатывать только информацию, представленную в числовой форме. Вся другая информация (звуки, изображения, показания приборов и т. д.) для обработки на компьютере должна быть преобразована в числовую форму. С помощью компьютерных программ можно преобразовывать полученную информацию, в том числе - текстовую. При вводе в компьютер каждая буква кодируется определенным числом, а при выводе на внешние устройства (экран или печать) для восприятия человеком по этим числам строятся изображения букв. Соответствие между набором букв и числами называется кодировкой символов. Как правило, все числа в компьютере представляются с помощью нулей и единиц, т.е. словами, компьютеры работают в двоичной системе счисления, поскольку при этом устройства для их обработки получаются значительно более простыми.

Необходимо отметить, что кодирование информации распадается на  определенные этапы: 1) Определение объёма информации, подлежащей кодированию. 2) Классификация и систематизация информации. 3) Выбор системы кодирования и разработка кодовых обозначений. 4) Непосредственное кодирование.

2.2Основные теоремы о кодах

В теории кодирования фундаментальное значение имеют две теоремы, доказанные известным американским ученым К. Шенноном, с которых, собственно, и началось развитие теории кодирования. Первая теорема Шеннона говорит о том, что при канале, не вносящем своих помех, можно закодировать сообщения таким образом, чтобы среднее число элементов кода, приходящихся на один элемент кодируемого алфавита, было бы минимальным (этот минимум определяется некоторым параметром H - энтропией источника информации, характеризующего статистические свойства источника). Такое кодирование называется эффективным статистическим кодированием[5].

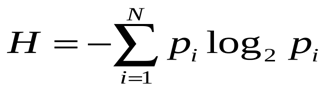
Вторая теорема Шеннона относится к каналам с искажениями (канал с помехами или шумами). Согласно этой теореме, для таких каналов всегда существует способ кодирования, при котором сообщения будут передаваться с какой угодно высокой достоверностью, если только скорость передачи не превышает пропускной способности канала связи.

Специальным разделом в теории кодирования является теория арифметических кодов, используемых для повышения надежности работы вычислительных устройств. Арифметические коды позволяют обнаруживать и исправлять ошибки, возникающие в арифметических устройствах ЭВМ. Правда, за такой сервис приходится расплачиваться лишним временем и оборудованием. Поэтому арифметические коды используются только в специальных ЭВМ, предназначенных для решения ответственных задач, когда ошибки в работе машины могут привести к весьма нежелательным последствиям (например, арифметические коды используются во многих ЭВМ, которые устанавливают на космических кораблях).

 Глава 3. Практика кодирования

3.1 Кодирование сигнала

Кодирование сигнала – это его представление в определенной форме, удобной для последующего использования сигнала, т.е. это правило, описывающее отображение одного набора знаков в другой набор знаков[6]. Тогда отображаемый набор знаков называется исходным алфавитом, а набор знаков, который используется для отображения, - кодовым алфавитом, или алфавитом для кодирования. При этом кодированию подлежат как отдельные символы исходного алфавита, так и их комбинации. Например, дана таблица соответствия между натуральными числами трёх систем счисления. Эту таблицу можно рассматривать как некоторое правило, описывающее отображение набора знаков десятичной системы счисления в двоичную и шестнадцатеричную. Тогда исходный алфавит - десятичные цифры от 0 до 9, а кодовые алфавиты - это 0 и 1 для двоичной системы; цифры от 0 до 9 и символы {A, B, C, D, E, F} - для шестнадцатеричной. Кодовой комбинацией (кодом) называется совокупность символов кодового алфавита, применяемых для кодирования одного символа (или одной комбинации символов) исходного алфавита. При этом кодовая комбинация может содержать один символ кодового алфавита. Исходным символом называется символ (или комбинация символов) исходного алфавита, которому соответствует кодовая комбинация. Например, поскольку 8 = 10002 и 8 является исходным символом, 1000 - это кодовая комбинация, или код, для числа 8. В то же время 8 - это исходный символ. Совокупность кодовых комбинаций называется кодом. Взаимосвязь символов (или комбинаций символов, если кодируются не отдельные символы) исходного алфавита с их кодовыми комбинациями составляет таблицу соответствия (таблицу кодов). Обратная процедура получения исходных символов по кодам символов называется декодированием. Очевидно, для выполнения равильного декодирования код должен быть однозначным, т.е. одному исходному символу должен соответствовать точно один код и наоборот.

В зависимости от целей кодирования, различают следующие его виды: кодирование по образцу - используется всякий раз при вводе информации в компьютер для её внутреннего представления; криптографическое кодирование, или шифрование, – используется, когда нужно защитить информацию от несанкционированного доступа; эффективное, или оптимальное, кодирование – используется для устранения избыточности информации, т.е. снижения ее объема, например, в архиваторах; помехозащитное, или помехоустойчивое, кодирование – используется для обеспечения заданной достоверности в случае, когда на сигнал накладывается помеха, например, при передаче информации по каналам связи.

Заключение

Создание компьютеров было бы невозможно, если одновременно с их появлением не была бы создана теория кодирования сигналов. Теория кодирования довольно молодая наука, получившая свое распространение благодаря основным теоремам Клода Шеннона. Задача кодирования является одним из главных понятий информатики, так как кодирование предшествует передаче и хранению информации, и, соответственно, является основой их успешного осуществления. Кодирование применяется  в целях унификации формы представления данных, которые относятся к различным типам, в целях автоматизации работы с информацией. Теория кодирования — одна из тех областей математики, которые заметно повлияли на развитие компьютинга. Ее область действия распространяется на передачу данных по реальным (или зашумленным) каналам, а предметом является обеспечение корректности переданной информации.

Список использованной литературы:

1.История кодирования  [Электронный ресурс]

URL: http://profbeckman.narod.ru/InformLekc.files (Дата обращения 31.03.2016)

2.Введение в теорию кодирования: учебное пособие/Ф.И.Соловьева - Новосиб. гос. ун-т. Новосибирск,2006.- 4 с.

3.Информация и информационные процессы. Социальная информатика/А.В.Могилев, Л.В.Листрова-СПб: БХВ Петербург,2006.- 39 с.

4.Общие понятия и элементы теории кодирования [Электронный ресурс]

URL:http://b.my-city.com.ua/news/4659/23/obschie-ponyatiya-i-elementy-teorii-kodirovaniya/ (Дата обращения 31.03.2016)

5.Основные понятия теории кодирования [Электронный ресурс]

URL: http://sga-informatika.ru/153302/95-412-basic-concepts-of-coding-theory

(Дата обращения 31.03.2016)

6.Другие важные понятия теории информации. Практика кодирования информации [Электронный ресурс]

URL: http://u4isna5.ru/konspektlekcii/35-lekciiinformatika/102-informatleccija4

(Дата обращения 31.03.2016)