
Институт информационных технологий
Кафедра вычислительной техники (ВТ)
Курсовой проект (работа)
по дисциплине
«Информатика»
Тема курсового проекта (работы)
«Построение комбинационных схем для полностью и не полностью определенных логических функций»
Студент группы ИВБ-1-14 Авдеев Д.Д.
Руководитель курсового проекта (работы) Жемчужникова Т.Н.
Работа представлена к защите « » 2014г.
«Допущен к защите» « » 2014г.
Москва, 2014
|
|
|
|
|
||
|
||
|
Институт информационных технологий (ИТ) |
|
|
Кафедра вычислительной техники (ВТ) |
|
Утверждаю
Заведующий кафедрой С.М.Коваленко
«___ »__________ 201_г.
|
ЗАДАНИЕ |
|
на выполнение курсового проекта (работы) |
|
по дисциплине «Информатика» |
Студент Авдеев
Д.Д.
Группа ИВБ-1-14
1. Тема «Построение комбинационных схем для полностью и не полностью определенных логических функций»
2. Исходные данные:
− Диаграммы Вейча для полностью определенных логических функций.
− Диаграммы Вейча для полностью определенных логических функций.
− Аппарат булевой алгебры.
− Способы минимизации логических функций.
3. Перечень вопросов, подлежащих разработке, и обязательного графического материала:
− Построение таблицы истинности по диаграммам Вейча.
− Построение не минимизированной логической схемы на элементах Шеффера.
− Построение не минимизированной логической схемы на элементах Вебба.
− Построение минимизированной не полностью логической схемы на элементах Шеффера.
− Построение минимизированной не полностью логической схемы на элементах Вебба.
− Построение минимизированной полностью логической схемы на элементах Шеффера.
− Построение минимизированной полностью логической схемы на элементах Вебба.
|
Задание на курсовой проект (работу), выдала |
«____» |
________ 201_г. |
Жемчужникова Т.Н. |
|
|
Задание на курсовой проект (работу), получил |
«____» |
________ 201_г. |
Авдеев Д.Д. |
|
Задание 1.
1. Перевести из 10→2 число: 17,9
2. Перевести из 10→8→2 число: 17,9
3. Перевести из 10→16→2 число: 17,9
4. Представить отрицательное число X = - 0,1010:
· в обратном коде: [X] обр. = ?
· в обратном модифицированном коде: [X] обр. мод. = ?
5. Представить отрицательное число X = - 0,0100:
· в дополнительном коде: [X] доп. = ?
· в дополнительном модифицированном коде: [X] доп. мод. = ?
6. Заменить операцию вычитания в прямом коде на операцию сложения в обратном и обратном модифицированном коде:
|
X = + 0,1100 |
[X]обр. = ? |
[X]обр.мод. = ? |
|
|
Y = + 0,1010 |
[Y]обр. = ? |
[Y]обр.мод. = ? |
|
|
X - Y = ? |
[X]обр. + [Y]обр. = ? |
[X]обр.мод. + [Y]обр.мод. = ? |
7. Заменить операцию вычитания в прямом коде на операцию сложения в дополнительном и дополнительном модифицированном коде:
|
X = + 0,1100 |
[X]доп. = ? |
[X]доп.мод. = ? |
|
|
Y = + 0,1010 |
[Y]доп. = ? |
[Y]доп.мод. = ? |
|
|
X - Y = ? |
[X]доп. + [Y]доп. = ? |
[X]доп.мод. + [Y]доп.мод. = ? |
[X]доп. = ? [Y]доп. = ?

[X]доп. + [Y]доп. = ?
[X]доп.мод. = ? [Y]доп.мод. = ?
[X]доп.мод. + [Y]доп.мод. =
8. Построить конституенту "1" и конституенту "0" для следующих аргументов:
А = 0; В = 0; С = 0; D = 1
9. По заданной таблице истинности записать логическую функцию в виде ДНФ и КНФ:
|
a |
b |
c |
f |
|
|
0 |
0 |
0 |
0 |
|
|
0 |
0 |
1 |
0 |
|
|
0 |
1 |
0 |
0 |
|
|
0 |
1 |
1 |
1 |
|
|
1 |
0 |
0 |
0 |
|
|
1 |
0 |
1 |
1 |
|
|
1 |
1 |
0 |
1 |
|
|
1 |
1 |
1 |
1 |
ДНФ f(a,b,c) = ? КНФ f(a,b,c) = ?
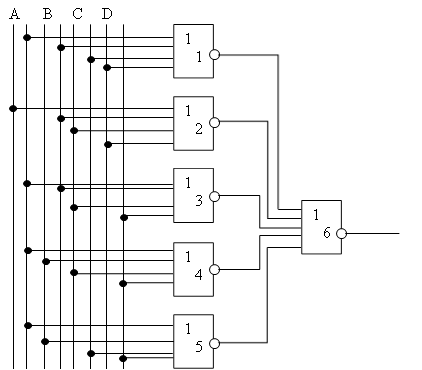
10. Построить комбинационную схему на элементах "И-НЕ".
11. Построить комбинационную схему на элементах "ИЛИ-НЕ".
Задание 1. Вариант 10.
1. 10 → 2
17,910 = 10001,1110012
|
17 |
2 |
0 |
9 |
||||||||
|
|
8 |
1 |
8 |
||||||||
|
0 |
4 |
1 |
6 |
||||||||
|
|
|||||||||||
|
0 |
2 |
1 |
2 |
||||||||
|
0 |
4 |
||||||||||
|
0 |
1 |
||||||||||
|
0 |
8 |
||||||||||
|
1 |
6 |
2. 10→8→2
17,910 = 21,7146318 = 10001,111001100112
|
|
8 |
0 |
9 |
||
|
|
2 |
7 |
2 |
||
|
1 |
6 |
||||
|
4 |
8 |
||||
|
6 |
4 |
||||
|
3 |
2 |
||||
|
1 |
6 |
3. 10→16→2
17,910 = 11Е616 = 10001.111001100112
4. X = -0,1010
[X] обр = 1,0101
[X] обр. мод = 11,0101
5. Х = -0,1100
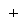
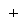


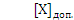 = 1,0011
= 1,0011 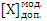 = 11,0011
= 11,0011
1 1
1,0111 11,0111
[X] доп. мод. = 11,0111
6.
1 1
1
1 1

 x = 0,1100
[x] обр. = 0,1100 [x] обр.
мод. = 00,1100
x = 0,1100
[x] обр. = 0,1100 [x] обр.
мод. = 00,1100
y = 0,1010 [y] обр. = 1,0101 [y] обр. мод. = 11,0101






 x – y = 0,0010
[x] обр. + [y] обр.=1 0,0001 [x]
обр. мод. + [y] обр. мод. =1 00,0001
x – y = 0,0010
[x] обр. + [y] обр.=1 0,0001 [x]
обр. мод. + [y] обр. мод. =1 00,0001



 1
1
1
1

 0,0010
00,0010
0,0010
00,0010
7.
1 1 1

 x = 0,1100 [x]
доп. = 0,1100 [x] доп. = 0,1100
x = 0,1100 [x]
доп. = 0,1100 [x] доп. = 0,1100
 y = 0,1010
[y] доп. = 1,0101 [y]
доп. = 1,0110
y = 0,1010
[y] доп. = 1,0101 [y]
доп. = 1,0110




 x – y = 0,0010
1
0,0010
x – y = 0,0010
1
0,0010


 1,0110
1,0110
1 1 1
 [x] доп. мод. = 00,1100
[x] доп. мод. = 00,1100
[y] доп. мод. = 11,0110




 00,0010
00,0010
8. A = 0, B = 0, C = 0, D = 1.
f 1 = A̅˄B̅˄C̅˄D = A̅&B̅&C̅&D = A̅*B̅*C̅*D
f 0 = A˅B˅C˅D
9.  = a̅ . b . c
˅ a . b̅ . c ˅ a . b . c̅
˅ a . b . c
= a̅ . b . c
˅ a . b̅ . c ˅ a . b . c̅
˅ a . b . c
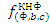 = (a ˅ b ˅ c) ˄ (a ˅ b
˅ c̅) ˄ (a ˅ b̅ ˅ c) ˄
(a̅ ˅ b ˅ c)
= (a ˅ b ˅ c) ˄ (a ˅ b
˅ c̅) ˄ (a ˅ b̅ ˅ c) ˄
(a̅ ˅ b ˅ c)
10. Комб. схема «И - НЕ»







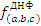 = a̅
. b . c ˅ a . b̅ .
c ˅ a . b . c̅ ˅ a . b .
c = a̅ . b
. c ˅ a . b̅ . c ˅ a . b
. c̅ ˅ a . b . c
= a̅
. b . c ˅ a . b̅ .
c ˅ a . b . c̅ ˅ a . b .
c = a̅ . b
. c ˅ a . b̅ . c ˅ a . b
. c̅ ˅ a . b . c
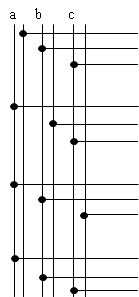



















11. Комб. схема «ИЛИ - НЕ»



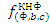 =
(a ˅ b ˅ c)
˄ (a ˅ b ˅ c̅) ˄ (a ˅ b̅ ˅
c) ˄ (a̅ ˅ b ˅ c) =
=
(a ˅ b ˅ c)
˄ (a ˅ b ˅ c̅) ˄ (a ˅ b̅ ˅
c) ˄ (a̅ ˅ b ˅ c) =



 = (a ˅ b ˅
c) ˄ (a ˅ b ˅ c̅) ˄ (a ˅ b̅
˅ c) ˄ (a̅ ˅ b ˅ c)
= (a ˅ b ˅
c) ˄ (a ˅ b ˅ c̅) ˄ (a ˅ b̅
˅ c) ˄ (a̅ ˅ b ˅ c)































 |
||||||||
 |
||||||||
 |
||||||||
 |
||||||||
 |
||||||||
 |
||||||||
 |
||||||||
 |
||||||||
 |
Задание 2.
 |
|||||
 |
|||||
 |
|||||
|
|
0 |
1 |
|
|
0 |
1 |
* |
|
|
|
0 |
1 |
* |
|
* |
1 |
1 |
|


 |
|||
 |
|||
|
|
0 |
1 |
|
|
0 |
1 |
1 |
|
|
|
0 |
1 |
1 |
|
1 |
1 |
1 |
|


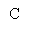

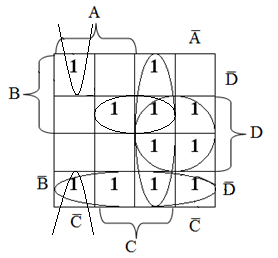
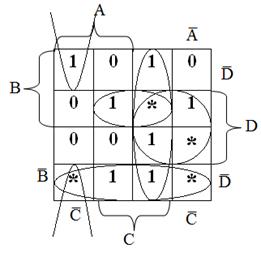
ДНФ




 ДНФ: f(a,b,c,d)
= S ˅ M = S ˅ M = S ˄ M
ДНФ: f(a,b,c,d)
= S ˅ M = S ˅ M = S ˄ M
S = A . B . C̅ . D̅ ˅ A̅ . B . C . D̅ ˅ A . B . C . D ˅ A̅ . B . C . D ˅ A̅ . B . C̅ . D ˅ A̅ . B̅ . C . D =
 |
|
 |
A . B . C̅ . D̅ ˅ A̅ . B . C . D̅ ˅ A . B . C . D ˅ A̅ . B . C . D ˅ A̅ . B . C̅ . D ˅ A̅ . B̅ . C . D =
 |
||||||||||||
 |
 |
 |
 |
 |
 |
A . B . C̅ . D̅ ˅ A̅ . B . C . D̅ ˅ A . B . C . D ˅ A̅ . B . C . D ˅ A̅ . B . C̅ . D ˅ A̅ . B̅ . C . D
M = A̅ . B̅ . C̅ . D ˅ A . B̅ . C̅ . D̅ ˅ A . B̅ . C . D̅ ˅ A̅ . B̅ . C . D ˅ A̅ . B̅ . C̅ . D̅ =
 |
|
 |



 A̅
. B̅ . C̅ . D ˅ A . B̅ . C̅ . D̅ ˅ A . B̅ . C . D̅ ˅ A̅ . B̅ . C . D ˅
A̅ . B̅ . C̅ . D̅ =
A̅
. B̅ . C̅ . D ˅ A . B̅ . C̅ . D̅ ˅ A . B̅ . C . D̅ ˅ A̅ . B̅ . C . D ˅
A̅ . B̅ . C̅ . D̅ =
 |
|||||||||
 |
 |
 |
|||||||
 |
 |
A̅ . B̅ . C̅ . D ˅ A . B̅ . C̅ . D̅ ˅ A . B̅ . C . D̅ ˅ A̅ . B̅ . C . D ˅ A̅ . B̅ . C̅ . D̅
КНФ
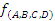 = (A
. B . C
. D̅) ˅
(A̅ . B . C̅ . D̅)
˅ (A . B . C̅ . D) ˅ (A . B̅ . C̅ .
D) ˅ (A .
B̅ . C . D) =
= (A
. B . C
. D̅) ˅
(A̅ . B . C̅ . D̅)
˅ (A . B . C̅ . D) ˅ (A . B̅ . C̅ .
D) ˅ (A .
B̅ . C . D) =
 |
|||
 |
(A̅ ˅ B̅ ˅ C̅ ˅ D) ˄ (A ˅ B̅ ˅ C ˅ D) ˄ (A̅ ˅ B̅ ˅ C ˅ D̅) ˄ (A̅ ˅ B ˅ C ˅ D̅) ˄ (A̅ ˅ B ˅ C̅ ˅ D̅) =
 |
||||||||||
 |
 |
 |
 |
 |
(A̅ ˅ B̅ ˅ C̅ ˅ D) ˄ (A ˅ B̅ ˅ C ˅ D) ˄ (A̅ ˅ B̅ ˅ C ˅ D̅) ˄ (A̅ ˅ B ˅ C ˅ D̅) ˄ (A̅ ˅ B ˅ C̅ ˅ D̅)
 |
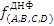
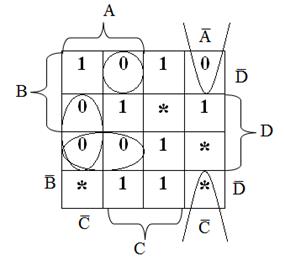
КНФmin (без звездочек)
 |
|||
 |
|||
|
|
|
1 |
|
|
|
1 |
1 |
|
|
|
0 |
1 |
1 |
|
1 |
1 |
1 |
|




 |
||||
 |
||||
 |
||||
 |








 |
|||||
 |
|||||
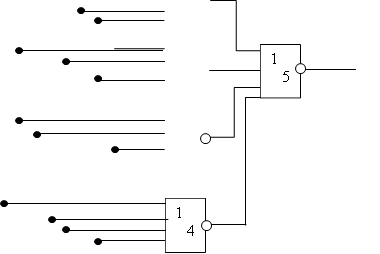 |
ДНФmin (без звездочек)
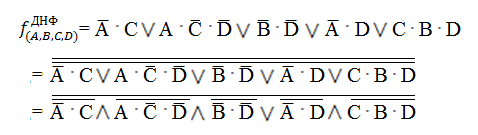
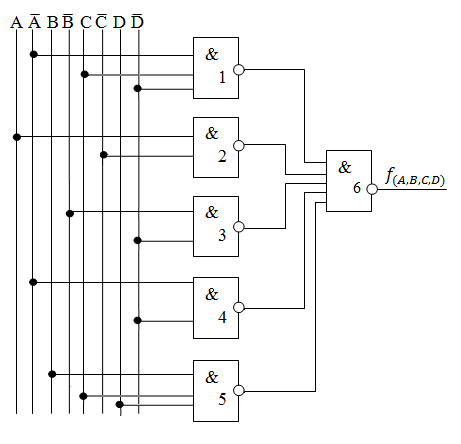
ДНФmin (со звездочками)
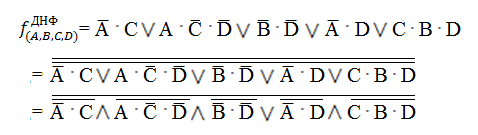

 КНФmin (со звездочками)
КНФmin (со звездочками)
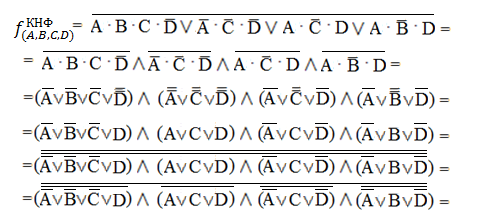
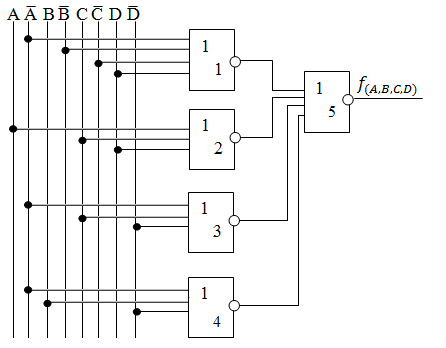
Сравнительные таблицы по кол-ву необходимых элементов.
|
«И-НЕ» |
Кол-во элементов |
||||
|
2-входовых |
3-входовых |
4-входовых |
5-входовых |
6-входовых |
|
|
Без минимизации |
3 |
0 |
11 |
1 |
1 |
|
Минимизация (без звездочек) |
3 |
2 |
0 |
1 |
0 |
|
Минимизация (со звездочками) |
3 |
2 |
0 |
1 |
0 |
|
«ИЛИ-НЕ» |
Кол-во элементов |
|||
|
2-входовых |
3-входовых |
4-входовых |
5-входовых |
|
|
Без минимизации |
0 |
0 |
5 |
1 |
|
Минимизация (без звездочек) |
0 |
2 |
3 |
0 |
|
Минимизация (со звездочками) |
0 |
3 |
2 |
0 |
|
Элементы Шеффера |
Элементы Вебба |
|||||
|
Без мин. |
С мин. |
С мин. и * |
Без мин. |
С мин. |
С мин. и * |
|
|
Кол-во элементов |
16 |
6 |
6 |
6 |
5 |
5 |
|
Кол-во связей |
61 |
17 |
17 |
25 |
18 |
18 |
Вывод:
Проведя анализ данных таблиц,
можно сделать вывод, что минимизация ведёт к сокращению количества
используемого оборудования.
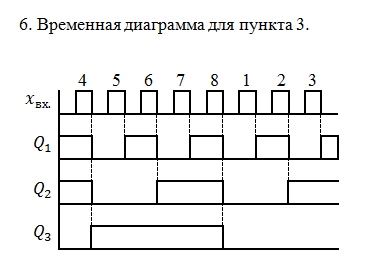
Задание 3.
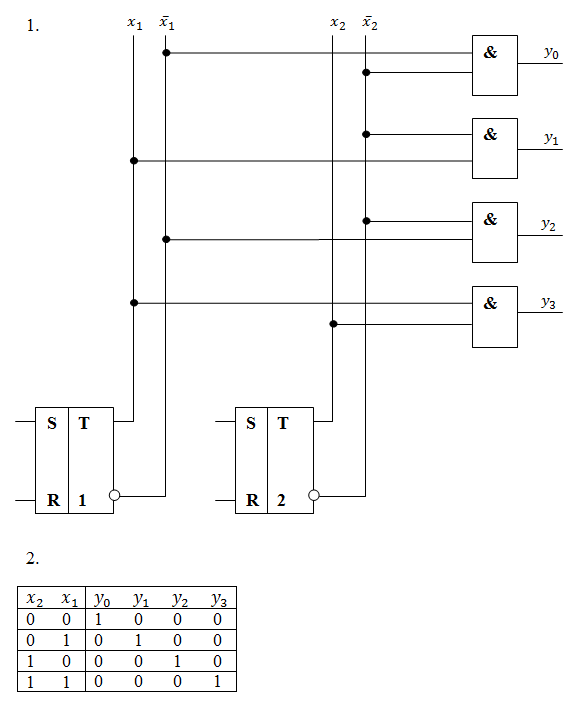
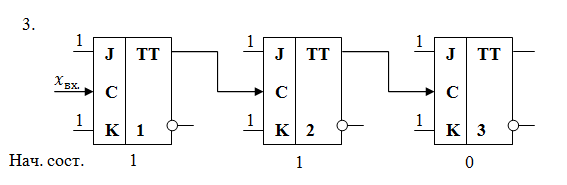
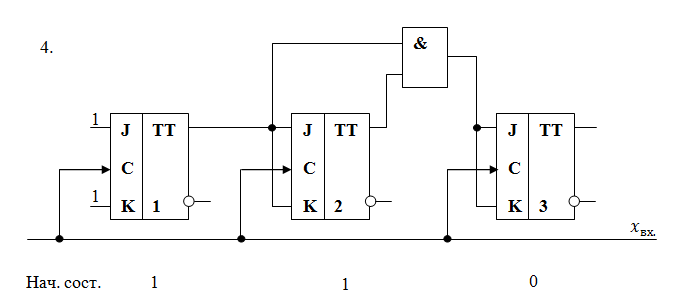
Задание 4.

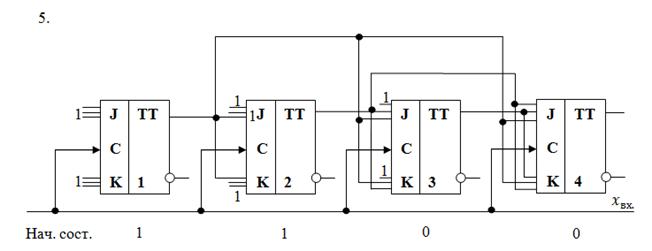
Задание 5.















 1
1
 17
17 1
1
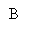 1
1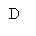
 1
1 0
0
 0
0 (zip - application/zip)
(zip - application/zip)










