Целочисленное программирование. Циклический алгоритм. Модели Леонтьева

Содержание

Введение

1. Целочисленное программирование

1.1 Целочисленное программирование. Общие понятия.

1.2 Циклический алгоритм целочисленного программирования.

2. Модели Леонтьева

2.1 Модель Леонтьева многоотраслевой экономики

2.2 Продуктивные модели Леонтьева

Заключение

Приложение 1

Список литературы

Введение

Моделирование в научных исследованиях стало применяться еще в глубокой древности и постепенно захватывало все новые области научных знаний: техническое конструирование, строительство и архитектуру, астрономию, физику, химию, биологию и, наконец, общественные науки. Большие успехи и признание практически во всех отраслях современной науки принес методу моделирования ХХ в. Однако методология моделирования долгое время развивалась независимо отдельными науками. Отсутствовала единая система понятий, единая терминология. Лишь постепенно стала осознаваться роль моделирования как универсального метода научного познания. Термин "модель" широко используется в различных сферах человеческой деятельности и имеет множество смысловых значений. Рассмотрим только такие "модели", которые являются инструментами получения знаний. Модель – это такой материальный или мысленно представляемый объект, который в процессе исследования замещает объект-оригинал так, что его непосредственное изучение дает новые знания об объекте-оригинале.

Моделирование – это основной специфический метод науки, который используется для анализа и синтеза систем управления. Это особенный познавальный способ, когда субъект исследования вместо непосредственного исследуемого объекта познания выбирает или создает подобный ему вспомогательный объект – образ или модель, исследует его, а полученные новые знания переносит на объект-оригинал. Благодаря активной роли субъекта сам процесс моделирования имеет творческий, активный характер.

Под задачей целочисленного программирования (ЦП) понимается задача, в которой все или некоторые переменные должны принимать целые значения. В том случае, когда ограничения и целевая функция задачи представляют собой линейные зависимости, задачу называют целочисленной задачей линейного программирования. В противном случае, когда хотя бы одна зависимость будет нелинейной, это будет целочисленной задачей нелинейного программирования. Особый интерес к задачам ЦП вызван тем, что во многих практических задачах необходимо находить целочисленное решение ввиду дискретности ряда значений искомых переменных.

1.Целочисленное программирование

1.1 Целочисленное программирование. Общие понятия.

При рассмотрении целого ряда задач финансового менеджмента и бизнеса необходимо учитывать требование целочисленности использу­емых переменных. Такие задачи называются задачами целочисленного программирования.

Целочисленным (иногда его называют также дискретным) программированием называется раздел математического программирования, изучающий экстремальные задачи, в которых на искомые переменные накладывается условие целочисленности, а область допустимых решений конечна. Огромное количество экономических задач носит дискретный, чаще всего целочисленный характер, что связано, как правило с физической неделимостью многих элементов расчета: например, нельзя построить два с половиной завода, купить полтора автомобиля  и т.д. В ряде случаев такие задачи решаются обычными методами, например, симплексным методом, с последующим округлением до целых чисел. Однако такой подход оправдан, когда отдельная единица составляет очень малую часть всего объема (например, товарных запасов); в противном случае он может внести значительные искажения в действительно оптимальное решение. Поэтому разработаны специальные методы решения целочисленных задач.

 Рекомендации по формулировке и решению ЦП

1.     Количество целочисленных переменных уменьшать насколько возможно. Например, целочисленные переменные, значения которых должно быть не менее 20, можно рассматривать как непрерывные.

2.     В отличие от общих задач ЛП, добавление новых ограничений особенно включающих целочисленные переменные, обычно уменьшают время решения задач ЦП.

3.     Если нет острой необходимости в нахождении точного оптимального целочисленного решения, отличающегося от непрерывного решения, например, 3%. Тогда реализацию метода ветвей и границ для задачи максимизации можно заканчивать, если отношение разницы между верхней и нижней границ к верхней границы меньше 0,03.

Метод ветвей и границ можно применять для решения задач нелинейного программирования.

1.2 Циклический алгоритм целочисленного программирования.

Рассмотрим следующую задачу линейного программирования:

Максимизировать

X₀=a₀₀-a₀₁x₁-a₀₂x₂-……..-a_0nx_n,

при условии

x_n+1=a_n+1,0-a_n+1,1x₁-a_n+1,2x₂-…….-a_n+1,nx_n,

_.

_.

 

x_n+m=a_n+m,0- a_n+m,1x₁-a_n+m,2x₂-…….-a_n+m,nx_n,

                              x_j≥0         (j=1,…….,n+1,…….,n+m).

Заметим, что x_n+1,  . ., х_n+m  — слабые переменные, a x₁ ... ., х_n  — исходные переменные задачи (1). Если наряду с огра­ничениями (1) потребовать, чтобы все х_j , (j"=1, . . ., т) были целыми, то задача будет называться задачей целочисленного про­граммирования. Существует большое количество задач, особенно комбинаторных, которые можно сформулировать как задачи цело­численного программирования.

Ограничения (1) определяют выпуклую область OABCD в n-мер­ном пространстве, как показано на рис.1. Узлы целочисленной решетки на рис.1 изображены точками. Такие точки, рас­положенные внутри области OABCD, являются допустимыми решениями задачи целочисленного программирования. Оптималь­ные решения задачи линейного программирования всегда распола­гаются на границе области решений. В данном случае граничные точки не являются даже допустимыми решениями, поскольку ни одна из них не целочисленна. Предположим, что область допу­стимых решений сужена до выпуклой оболочки допустимых целых точек внутри допустимой области. На рис. 13.1 эта выпук­лая оболочка показана затененной областью OEFGH. Эту зате­ненную область можно рассматривать как область допустимых решений некоторой другой задачи линейного программирования. Действительно, если к задаче линейного программирования, опре­деляющей допустимую область OABCD, добавить ограничение типа RR", как показано на рис. 13.1, то вновь полученная задача будет иметь OEFGH в качестве области допустимых решений. Такая вновь полученная область обладает двумя важными свой­ствами: во-первых, она содержит все допустимые целочисленные точки исходной задачи линейного программирования (поскольку она является выпуклой оболочкой этих точек), во-вторых, все крайние точки новой области — целочисленны. Поэтому любое базисное оптимальное решение модифицированной задачи линей­ного программирования имеет своими компонентами целые числа и является оптимальным ре­шением исходной задачи цело­численного программирования.

Именно алгоритмы цело­численного программирова­ния, которые будут описаны   ниже, реализуют методы  систематического введения дополнительных ограничений с целью сведения исходной до­пустимой области к выпуклой оболочке ее допустимых цело­численных точек.

Как только это будет сде­лано, можно решать моди­фицированную задачу линей­ного программирования лю­бым обычным методом, и полученное базисное опти­мальное решение автоматически будет целочисленным. Представ­ленный ниже целочисленный алгоритм обладает следующими свойствами: 1) все дополнительные ограничения сохраняют допустимые точки исходной целочисленной задачи; 2) за конеч­ное число шагов создается достаточное количество дополнитель­ных ограничений для того, чтобы оптимальное решение моди­фицированной задачи было целочисленным; 3) дополнительные ограничения (гиперплоскости) проходят по крайней мере через одну целочисленную точку, хотя и не обязательно находящуюся внутри выпуклой оболочки; 4) каждое новое ограничение сокра­щает область допустимых решений исходной задачи целочислен­ного программирования. Следует подчеркнуть, что оптимальное решение исходной задачи может быть получено прежде, чем допустимая область сократится до размеров выпуклой оболочки. К тому же, поскольку оптимальное целочисленное решение определяется пересечением п гиперплоскостей, таких гиперпло­скостей существует не более, чем это необходимо; некоторыеизних могут быть ограничениями исходной задачи.

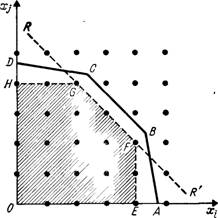
Рис, 1.

2. Модели Леонтьева

2.1 Модель Леонтьева многоотраслевой экономики

Эффективное ведение народного хозяйства предполагает наличие баланса между отдельными отраслями. Каждая отрасль при этом выступает двояко: с одной стороны, как производитель некоторой продукции, а с другой – как потребитель продуктов, вырабатываемых другими отраслями. Для наглядного выражения взаимной связи между отраслями пользуются определенного вида таблицами – так называемыми таблицами межотраслевого баланса. Идея таких таблиц была сформулирована в работах советских экономистов, а первая таблица опубликована в ЦСУ в 1926 г. Однако вполне развитая математическая модель межотраслевого баланса, допускающая широкие возможности анализа, появилась позже (1936 г.) в трудах экономиста В. Леонтьева. В данной работе я представлю её основное математическое содержание.

Итак, будем предполагать, что вся производящая сфера народного хозяйства разбита на некоторое число n отраслей, каждая из которых производит свой однородный продукт, причем разные отрасли производят разные продукты. Разумеется, такое представление об отрасли является в значительной мере абстракцией, так как в реальной экономике даже на отдельном предприятии производится значительное разнообразие выпускаемой продукции. Однако представление об отрасли в указанном выше смысле (как «чистой» отрасли) все же полезно, так как оно позволяет провести анализ сложившейся технологической структуры народного хозяйства, изучить функционирование народного хозяйства «в первом приближении».

Итак, предполагаем, что имеется n различных отраслей O₁, …, О_n, каждая из которых производит свой продукт. В процессе производства своего продукта каждая отрасль нуждается в продукции других отраслей (производственное потребление). Будем вести речь о некотором определенном промежутке времени [Т₀, Т₁](обычно таким промежутком служит плановый год) и введем следующие обозначения:

х_i – общий объем продукции отрасли i за данный промежуток времени – так называемый валовой выпуск отрасли i;

х_ij – объем продукции отрасли i, расходуемый отраслью j в процессе производства;

y_i – объем продукции отрасли i, предназначенный к потреблению в непроизводственной сфере, - объем конечного потребления.

Этот объем составляет обычно более 75% всей произведенной продукции. В него входят создаваемые в хозяйстве запасы, личное потребление граждан, обеспечение общественных потребностей (просвещение, наука, здравоохранение, развитие инфраструктуры и т.д.), поставки на экспорт.

Указание величины можно свести в табл. 1.1. Балансовый характер этой таблицы выражается в том, что при любом i = 1, …, n должно выполнять соотношение

х_i = х_i1 + х_i2 + … + х_in + у_i, (1.1)

означающее, что валовой выпуск х_i расходуется на производственное потребление, равное х_i1 + х_i2 + …+ х_in, и непроизводственное, равное у_i. Будем называть (1.1) соотношениями баланса.

Таблица 1.1

Производственное потребление	Конечное потребление	Валовой выпуск
х11 х12 … х1n х21 х22 … х 2n …………………… х n1 хn2 … хnn	у1 у2 … уn	х1 х2 … хn

Единицы измерения всех указанных величин могут быть или натуральными (кубометры, тонны, штуки и т.п.), или стоимостными; в зависимости от этого различают натуральный и стоимостный межотраслевой балансы. Для определенности в дальнейшем будем иметь в виду (если не оговорено противное) стоимостный баланс.

В. Леонтьев рассматривая развитие американской экономики в 30-е годы ХХ века, обратил внимание на важное обстоятельство. А именно величины 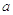_ij = 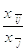 остаются постоянными в течение ряда лет. Это обусловливается примерным постоянством используемой технологии.

В соответствии со сказанным сделаем такое допущение: для выпуска любого объема х_j продукции отрасли j необходимо затратить продукцию отрасли i в количестве а_ij х_j, где а_ij – постоянный коэффициент. Проще говоря, материальные издержки пропорциональны объему производимой продукции. Это допущение постулирует, как говорится, линейность существующей технологии. Принцип линейности распространяют и на другие виды издержек (например, на оплату труда), а также на нормативную прибыль.

Итак, согласно гипотезе линейности имеем

х_ij = а_ijх_i (i, j = 1, …, n). (1.2)

Коэффициенты а_ij называют коэффициентами прямых затрат (коэффициентами материалоемкости).

Подставляя соотношения (1.2) в уравнение баланса (1.1), получаем систему n линейных уравнений относительно переменных х₁, х₂,…, х_n:

х₁ = а₁₁ х₁ + а₁₂ х₂ + … а_1n х_n + у₁,

х₂ = а₂₁ х₁ + а₂₂ х₂ + … а_2n х_n + у₂,

…………………………………..

х_n = а_n1 х₁ + а_n2 х₂ + … а_nn х_n + у_n,

или, в матричной записи,

х = Ах + у, (1.3)

где а₁₁ а₁₂ … а_1n х ₁ у₁

А = а₂₁ а₂₂ … а_2n , х = х ₂ , у = у₂ .

……………. … …

а_n1 а_n2 … а_nn  х_n у_n

Вектор х называется вектором валового выпуска, вектор у – вектором конечного потребления, а матрица А – матрицей прямых затрат. Соотношение (1.3) называется уравнением линейного межотраслевого баланса. Вместе с изложенной интерпретацией матрицы А и векторов х и у это соотношение называют также моделью Леонтьева.

2.2 Продуктивные модели Леонтьева

Определение. Матрица А ≥ 0 называется продуктивной, если для любого вектора у ≥ 0 существует решение х ≥ 0 уравнения

х = Ах + у (2.4)

В этом случае модель Леонтьева, определяемая матрицей А, тоже называется продуктивной. Другими словами, модель продуктивна, если любое конечное потребление у можно обеспечить при подходящем валовом выпуске х.

Уравнение Леонтьева (2.4) можно записать следующим образом:

(Е – А)х = у, (2.5)

где Е – единичная матрица. Возникает, естественно, вопрос об обращении матрицы Е – А. Понятно, что если обратная матрица (Е – А)^-1 существует, то из (2.5) вытекает

х = (Е – А)^-1 у. (2.6)

Теорема 1 (первый критерий продуктивности).

Матрица А ≥ 0 продуктивна только тогда, когда матрица (Е – А)^-1 существует и неотрицательна.

Доказательство.

Если матрица (Е – А)^-1 существует и неотрицательна, то из (2.6) сразу же следует продуктивность матрицы А.

Обратно, пусть матрица А продуктивна. Рассмотрим следующие системы уравнений:

(Е – А)х = е₁, (Е – А)х = е₂, …, (Е – А)х = е_n ,

Где е₁, е₂, …, е_n – столбцы единичной матрицы. Каждая из этих систем в силу продуктивности матрицы А имеет неотрицательное решение, т.е. существуют такие векторы (столбцы) с₁ ≥ 0, с₂ ≥ 0, …, с_n ≥ 0, что

(Е – А)с₁ = е₁, (Е – А)с₂ = е₂, …, (Е – А)с_n = е_n (2.7)

Обозначим через С матрицу, составленную из столбцов с₁ с ₂, …, с _n. Тогда вместо n равенств (2.7) можно написать одно:

(Е – А)С = Е.

Следовательно, матрица Е-А имеет обратную С, причем С ≥ 0.

Теорема доказана.

Теорема 2 (второй критерий продуктивности).

Неотрицательная квадратная матрица А продуктивна тогда и только тогда, когда её число Фробениуса меньше единицы.

Доказательство.

Пусть неотрицательная матрица А продуктивна. Тогда для любого неотрицательного вектора у существует решение х ≥ 0 уравнения (2.4) Пусть у > 0, тогда, очевидно, х > 0. Умножив равенство (2.4) слева на левый вектор Фробениуса р^Т_А и учитывая, что

р^Т_АА = λ_Ар^Т_А, (2.8)

получим

λ _А (р^Т_А х) + р^Т_А у = р^Т_А х,

или

(1 – λ_А)(р^Т_А х) = р^Т_А у.

Так как р^Т_А ≥ 0 и у ≥ 0, х ≥ 0, то р^Т_Ау > 0, р^Т_Ах > 0. Поэтому из последнего равенства вытекает, что λ_А < 1.

Обратно, пусть неотрицательная матрица А имеет число Фробениуса λ_А < 1. Покажем, что она продуктивна. Возьмем неотрицательный вектор у и покажем, что у системы (2.4) существует решение х ≥ 0.

Рассмотрим следующую неотрицательную матрицу размера (n + 1)(n+ 1):

а₁₁ а₁₂ … а_1n у₁

а₂₁ а₂₂ … а_2n у₂

А = …………….

а_n1 а_n2 … а_nn у_n

0 0 … 0 1

Где а_ij – элементы матрицы А и у₁, …, у_n – координаты вектора у. В более компактной форме матрицу можно записать так:

А = А у

0 1

Умножая эту матрицу слева на вектор р^Т = (0, …, 0,1), легко убедиться, что

р^ТА = р^Т.

Следовательно, одним из собственных значений матрицы А является вектор λ = 1.

Пусть вектор Х = (х₁ , …, х_n , х_n+1 ) = (х , х_n+1) является собственным вектором матрицы А, т.е. АХ = λХ. В силу определения матрицы А эторавносильно тому, что

А у х = λ х

0 1 х_n+1 х_n+1

или

Ах + у х_n+1 = λх,

х_n+1 = λ х_n+1. (2.9)

Если λ ≠ 1, то из второго соотношения системы (2.9) следует, что х_n+1 = 0, в силу чего первое уравнение имеет вид Ах = λх. Следовательно, λ – собственное значение матрицы А и, по нашему предположению ‌‌‌|λ| < 1. Таким образом, λ_А = 1 является положительным и максимальным по модулю собственным значением, следовательно является числом Фробениуса. По теореме Фробениуса-Перрона у матрицы А существует неотрицательный собственный вектор х_А = ( х_А , х_n+1), соответствующий λ_А =1. Очевидно, что х_n+1 ≠ 0, так как в противном случае из (2.9) следовало бы, что Ах = х. А это противоречит тому, что число Фробениуса λ_А < 1. Поэтому мы можем считать, что х_n+1 = 1. В силу того, что х_n+1 = 1, равенство (2.9) принимает вид

Ах_А + у = х_А.

Поскольку х_А = (х_А, х_n+1) ≥ 0, то х_А ≥ 0.

Следовательно, матрица А продуктивна.

Следствие.

Если для неотрицательной матрицы А и некоторыого положительного вектора у уравнение (2.4) имеет неотрицательное решение х, то матрица А продуктивна.

Доказательство.

Как было уже показано, из существования положительного решения у уравнения (2.4) следует, что λ_А < 1. На основании теоремы Фробениуса матрица А продуктивна.

Теорема 3 (третий критерий продуктивности).

Неотрицательная матрица А продуктивна тогда и только тогда, когда сходится бесконечный ряд

Е + А + А² + … (2.10)

Доказательство.

Пусть сходится ряд (2.10). Согласно лемме его сема равна (Е – А)^-1. При этом сумма указанного ряда будет неотрицательна, поскольку все слагаемые ряда неотрицательны. Итак, матрица (Е – А)^-1 существует и неотрицательна. Отсюда по теореме 1.3 следует продуктивность А.

Обратное утверждение (если А продуктивна, то ряд (2.10) сходится) доказывать не будем.

Заключение

Модель равновесных цен позволяет, зная величины норм добавленной стоимости, прогнозировать цены на продукцию отраслей. Она также позволяет прогнозировать изменение цен и инфляцию, являющиеся следствием изменения цены одной из отраслей.

Балансовый метод – это метод взаимного сопоставления ресурсов (материальных, трудовых, финансовых) и потребностей в них. Среди множества разновидностей балансового метода наиболее распространен межотраслевой баланс, увязывающий источники и направления использования ресурсов. Как правило, при применении балансового метода производятся вариантные расчеты с помощью вычислительной техники

Межотраслевой баланс представляет собой экономико-математическую модель народного хозяйства, что позволяет проводить многовариантные расчеты структуры общественного производства по заданному объему и структуре конечного продукта. Это имеет важное значение на предварительной стадии составления плана для осуществления вариантов расчетов пропорций, темпов и отраслевой структуры экономики, а также на последующих стадиях планирования для повышения уровня сбалансированности отраслей и анализа межотраслевых связей. Таким образом, разработка межотраслевого баланса является одной из предпосылок развития методологии оптимального планирования.

Данные полученные по модели межотраслевого баланса, дают возможность судить о тенденциях развития технического прогресса, о насыщении экономики производственными фондами, капитальными вложениями, трудовыми ресурсами и т.д. Такой анализ возможен на основе сопоставления матриц прямой и полной фондо-, капитало-, трудоемкости и др.

Межотраслевой баланс, разработанный в трудовых единицах, дает информацию, необходимую для построения рациональной системы цен.

Итак, балансовый метод заключает в себе использование балансов для взаимного сопоставления ресурсов (материальных, трудовых, финансовых) и потребностей в них.

В данной работе была рассмотрена сущность целочисленного программирования. Затронуты специальные методы решения целочисленных задач. Такие задачи возникают при моделировании разнообразных производственно-экономических, технических, военных и других ситуаций. В то же время ряд проблем самой математики может быть сформулирован как целочисленные экстремальные задачи.

Задачи такого типа весьма актуальны, так как к их решению сводится анализ разнообразных ситуаций , возникающих в экономике, технике, военном деле и других областях. Эти задачи интересны и с математической точки зрения. С появлением ЭВМ, ростом их производительности повысился интерес к задачам такого типа и к математике в целом.

Задача 1

Компания производит продукцию двух видов А и В. Обе требуют работы двух цехов сборочного и отделочного. Сведения о производстве:

Цех	Продукция	Вместе необходимо рабочих часов
А	В
Сборочный	3	5	15
Отделочный	5	2	10
Валовая прибыль на единицу	5	32

Компания заинтересована в наибольшей прибыльности этих комбинаций продукции. Найти сколько надо производить продукции А и В, чтобы валовая прибыль была максимальная.

Решение

Введем переменные:

х₁ – количество продукции вида А;

х₂ – количество продукции вида В.

Строим математическую модель:

F_мах = 5х₁ + 32х₂ при условиях:

3х₁ + 5х₂ ≤ 15;

5х₁ + 2х₂ ≤ 10.

х₁ ≥ 0, х₂ ≥ 0, т.к. продукция выпускаемая не может быть отрицательной.

Задачу можно решить графическим методом и можно решить или проверить симплекс-методом.

Для решения графическим методом запишем граничные прямые:

1) 3х₁ + 5х₂ = 15;

2) 5х₁ + 2х₂ = 10.

Строим граничные прямые на плоскости, но для этого найдем точки для построения прямых:

1)     х₂ = 0; х₁ = 5; х₁ = 0; х₂ = 3;

2)     х₂ = 0; х₁ = 2; х₁ = 0; х₂ = 5.

ОДЗ – многоугольник ОАВСD.

Для определения ОДЗ (области допустимых значений) необходимо найти направление полуплоскостей.

Для испытания берем точку О(0;0) и подставляем её координаты в неравенство (1) и (2), если неравенство удовлетворяется, то полуплоскость направлена к точке (0;0). При наложении полуплоскостей друг на друга получим ОДЗ.

Строим вектор целевой функции С, перпендикулярно к нему проводим линию уровня (пунктирная линия). Перемещаем линию уровня по ОДЗ в направлении вектора целевой функции С и самая дальняя точка от начала координат – это точка А(0;3) в ней х_опт.

Подставим координаты (0;3) в целевую функцию и получим её максимальное значение

F_mах = 5*0 + 3*32 = 96 ед. стоимости в точке А(0;3).

Для получения прибыли равной 96 ед.ст. необходимо включить в план продукцию типа В.

Список литературы

1. Акулич И.Л. Математическое программирование в примерах и задачах. – М.: Высшая школа, 2009.

2. Архангельский Ю.С., Коваленко И.И. Межотраслевой баланс. – К.: Выща шк. Головное изд-во, 2008.

3. Математика в экономике: Учебник: в 2-х ч. Ч.1/ А.С. Солодовников, В.А. Бабайцев, А.В. Браилов, И.Г. Шандра. – 2-е изд., перераб. и доп. – М.: Финансы и статистика, 2009.

4. В.Г.Карманов. Математическое программирование: Учебное пособие – 5-е издание, стереотип-М:ФИЗМАТ, 2011г.-264с.

5. А.В.Кузнецов, В.А.Сакович, Н.И.Холод. Высшая математика: Математическое программирование. Ученик - 2-е издание. 2001г. 351с.