Министерство транспорта Российской
Федерации
Федеральное государственное образовательное учреждение
ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ МОРСКОГО И РЕЧНОГО ФЛОТА
имени адмирала С.О.Макарова
 |
КАФЕДРА ОСНОВ СУДОВОЙ ЭЛЕКТРОЭНЕРГЕТИКИ
курсовая работа
«РАСЧЕТ И ВЫБОР СХЕМ ИЗМЕРИТЕЛЬНЫХ ПРЕОБРАЗОВАТЕЛЕЙ ТЕМПЕРАТУРЫ СУДОВЫХ ИИС»
Вариант №
Дата выполнения
Дата проверки
Выполнил: курсант гр. Э-23
Проверил: преподаватель
Санкт-Петербург 2015
Задание:
1) Определить основные параметры мостовой схемы R2, R3, R4, Rвых, Ucd, Iy, U0, E0, S
2) Вычислить питающее напряжение U0 с учетом допустимой мощности рассеивания в измеряемом сопротивлении (терморезисторе)
3) Рассчитать максимальную выходную мощность в указательной диагонали с учетом заданной погрешности при измерении температуры
4) Найти зависимости тока в указателе Iy от изменения первичного преобразователя(терморезистора)
5) Исследовать характер шкалы магнитоэлектрического преобразователя.
Исходные данные для курсовой работы
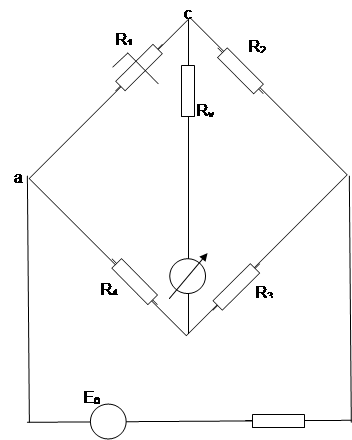 |
Ro
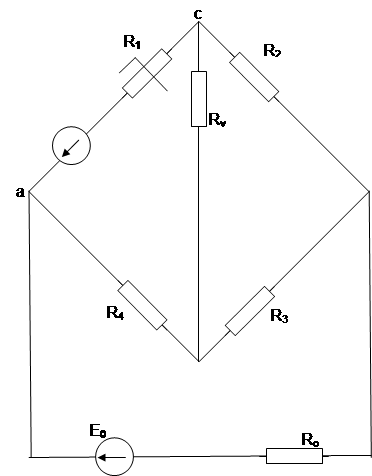
Рис1 Исследуемая схема мостовой цепи
Таблица1
|
R10, Ом |
Ry, Ом |
R0, Ом |
I, мА |
Погрешность
|
Материал |
Диапазон t,град С |
|
1080 |
19000 |
30 |
10 |
0,1 |
Медь |
-30…+45 |
Температурный коэффициент для
меди α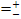 0,0043 0С-1
0,0043 0С-1
Для расчета основных параметров мостовой схемы необходимо учитывать условие равновесия моста:
R1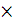 R3 = R2×R4; Uac = Uаd; Ubc = Ubd.
R3 = R2×R4; Uac = Uаd; Ubc = Ubd.
Вместе с тем известно, что равновесие моста наступает в момент, когда температура, измеренная терморезистором, равна 00С. Для получения наибольшей чувствительности сигнала измеряемого прибора при выходе моста из состояния равновесия используются пропорции, определяющие сопротивления резисторов в каждом плече диапазона.
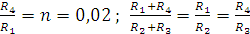 = 0,02
= 0,02
Используя пропорции, получим значения сопротивлений в плечах
R2 = 54000 [Ом]; R3 = 1080 [Ом]; R4 = 21,6[Ом]
Из условия равновесия моста известно, что тока в выходной диагонали нет, следовательно, зная сопротивления R10 иR2 и ток, проходящий через них, можно получить входное напряжение Uab
Uab = I1(R10+R2) = 550,8 [B]
Теперь, зная напряжение Uab, можно найти ток I2, проходящий через известные резисторыR3и R4
I2 = 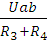 = 0,5 [A]
= 0,5 [A]
По первому закону Кирхгофа найдем ток в питающей диагонали моста I0
I0 = I1+I2 = 0,51 [A]
С помощью закона Ома активного участка цепи находим величину источника ЭДС Е0:
E0 = Uab + I0×R0 = 566,1
Для вычисления входного сопротивления мостовой схемы Rab применяется метод преобразования треугольника в эквивалентную схему звездой
Рис2 Эквивалентная схема
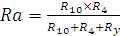 =1,16 [Ом]
=1,16 [Ом]
 =1020,8[Ом]
=1020,8[Ом]
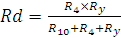 =20,4[Ом]
=20,4[Ом]
 =1078,8[Ом]
=1078,8[Ом]
По этому принципу находим выходное сопротивление моста Rcd
П = R1×R2×R3+R3×R2×R4+ R3×R4×R1+ R4×R2×R1= 65 530 218 240
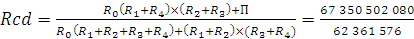 = 1080 [Ом]
= 1080 [Ом]
Находится ток в выходной диагонали:
∑y=  , где
, где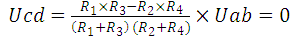 [B];Iy = 0 [A]
[B];Iy = 0 [A]
Особое значение – чувствительность, т.к. выходной сигнал является измеряемой величиной и значит должен быть достаточным для приведения прибора в действие, требуемого класса точности.
При изменении температуры изменяется сопротивление терморезистора на определенную величину ∆R1 с учетом заданной погрешности.
R1 = R10 (1+α×∆t) = 1080,5[Ом]
∆R1= R1 – R10 = 0,5
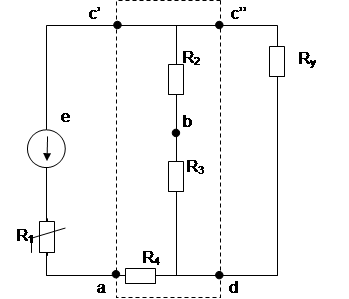
В итоге получаем схему с 2-мя источниками ЭДС: E0иl. При этом, сохраняется условие равновесия моста. Вследствие этого, входное напряжение от источника E0не влияет на ток в указателе, при этом эквивалентная схема примет вид (рис.4)
 |
|||
 |
|||
Лучшая передача энергии требует согласия сопротивлений, т.е. равенство входного сопротивления четырехполюсника внутреннему сопротивлению генератора. При этом максимальная мощность, отдаваемая генератором будет:
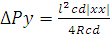 = 0,56×10-8 [B]
= 0,56×10-8 [B]
где 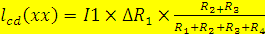 = 0, 0049ecd
= 0, 0049ecd
Мощность в указателе достигает номинального значения (∆Px) = (∆P0), в случае если:
n = 0 (R4=0)
m= 0 (R2+R3=∞)
∆P0
=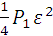 , где
, где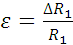 = 0,46×10-3
= 0,46×10-3
∆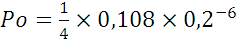 = 0,57×10-8
= 0,57×10-8
Точное условие моста, с точки зрения чувствительности приводит к разному возрастанию мощности, потребляемой всей мостовой схемой
P = P1+P2+P3+P4 = 280,9[Вт]
P1 = I12×R1 = 0,108 [Вт]
P2 = I12×R2 = 5,4[Вт]
P3=I12×R3
=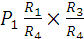 = 270[Вт]
= 270[Вт]
P4 = 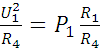 = 5,4[Вт]
= 5,4[Вт]
Сопоставляя ∆P0 и ∆Py, находим, что n = 0,02 и m = 0,02 различие между ними составляет ≈ 20%
В настоящее время на судах широкое применение нашли неуравновешенные мосты для измерения температуры в значительных диапазонах с обеспечением требований точности. Следовательно, необходимо исследовать характер шкалы магнитно-электрического указателя, включенного в диагональ моста. Для этого необходимо вычислить зависимость тока в указателе от изменения сопротивления одного из плеч.
На схеме отображаем приращение сопротивления к выводу моста:


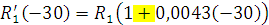 =940,68 [Ом]
=940,68 [Ом]
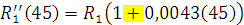 = 1289[Ом]
= 1289[Ом]
Находим питающее напряжение Uoс учетом допускаемой мощности рассеивания в терморезисторе
Uo = I1(R10+∆R1+R2)= 550,8 [B]
ТокIy найдем по формуле:
 ,где
,где
a = (Ry+R2)×(R3+R4)+R3×R4+Ro(Ry+R2+R3)= 82 662 528[Ом]
b = Ry(R1+R2)×(R3+R4)+R1×R2×(R3+R4)+Ro(Ry(R1+R2+R3+R4)+
+(R1+R4)×(R2+R3)) = 1 250 935 539 840 [Ом]
Для (-30⁰) Iy= -0,7×10-4 [A]без округления в маткаде 0, 6872
Для (45⁰) Iy = 0,1×10-3 [A] без округления в маткаде 0,007
Т.к. a и b состоят из постоянных величин, можем сделать вывод, что зависимость функции является функцией приращения сопротивления. Построим эту зависимость в виде графика, его значения определяют все параметры моста. При построении кривой получим чувствительность шкалы указателя.
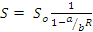 =5,2×10-7
=5,2×10-7
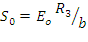 = 4,887×10-7
= 4,887×10-7
Определяем входное сопротивление относительно зажимов:
 = 15 133 [Ом]
= 15 133 [Ом]
Отклонение кривой 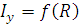 от касательной к ней определяет степень
неравномерности шкал
от касательной к ней определяет степень
неравномерности шкал
D= 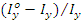 , где
, где 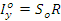
Для (-30)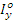 = -0,7×10-4без округления в
маткаде 0,68
= -0,7×10-4без округления в
маткаде 0,68
Для (45) 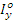 = 0,1×10-3без округления в
маткаде 0,1021
= 0,1×10-3без округления в
маткаде 0,1021
Отрезки EF, E’F’
(-30) 
(45) =
=
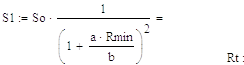
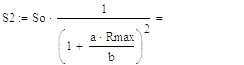














 t, град С
t, град С (zip - application/zip)
(zip - application/zip)










