Оценка эффективности стратегий.

Автономное образование учреждение высшего профессионального образования   

           Курская академия государственной и муниципальной службы.

 Кафедра «Информационной и техносферной безопасности и правовой защиты

                                                      информации».

    Реферат по дисциплине «Теория игр» на тему:

             «Оценка эффективности стратегий.

          Принцип гарантированного результата».

                                                                     Выполнила студентка

                                                                                
                        2 курса гр. «экономика – 411»

                                                                                                     
   Сайкова А. А.

                                                                                
                        Проверил преподаватель

                                                                                                        Погосян С. Л.

                                                            2012

Содержание.

1.     Теория игр………………………………………………………………3

2.     Представление игр………………………………………......................6

3.     Применение теории игр…………………………………......................8

4.     Типы игр. Кооперативные и некооперативные……………………...10

5.     Классификация игр………………………………………………….....12

6.     Оценка эффективности стратегий.

Принцип гарантированного результата……………………………….....14

7.     Примеры оценки эффективности и гарантированного результата…16

8.     Список используемой литературы……………………………………20

Теория игр.

Теория игр (Game theory) – это теория поведения продавцов или, иными словами, игроков в условиях, когда принимаемые решения одного из них незамедлительно влияют на решения остальных. Наиболее общим и простым примером теории игр может быть случай экономической войны между какими-либо двумя продавцами, ведущейся за рынок сбыта с помощью снижения цены. Каждый продавец будет снижать цену на свой продукт в ответ на снижение цены его конкурентом. В упрощенном случае результатом, при котором цены конкурентов совпадут, будет ноль. Эта ситуация отражена на графике 1.

Несколько иным примером является ситуация, представленная с помощью платежной матрицы, показанной на графике. 2. Как мы видим, матрица образована двухсторонней таблицей, состоящей из четырех квадратов, каждый из которых представляет результат самостоятельно принятых решений каждого из двух продавцов.

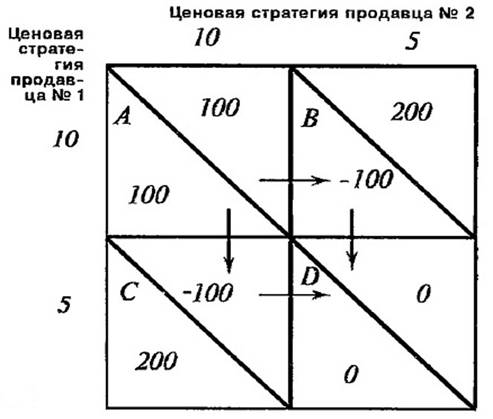
Квадрат А показывает начальную стадию конкурентной борьбы двух продавцов, каждый из которых при цене в 10 денежных единиц получает прибыль в размере 100 тыс. Решение продавца № 2 снизить цену принесет ему 200 тыс. прибыли при цене в 5 единиц, но его конкурент потеряет при этом 100 тыс. (квадрат В). Такого же результата добьется и продавец № 1, действуя аналогичным образом (квадрат С). В результате, конечным итогом их совместных действий станет положение, которое уравняет их статус по отношению друг к другу (квадрат D). Это положение, называемое равновесием Нэша (Nash equmbrium), принесет каждому из них нулевую прибыль. Таким образом, конечным результатом эгоистических, самостоятельных решений каждого из продавцов будет результат, который вреден им обоим.

Иными словами, самостоятельные решения каждого из продавцов в конкурентной борьбе «невидимой рукой» А.Смита приводят их к нулевой прибыльности, что полезно в целом для общества, но не совсем выгодно для отдельного продавца. Отсюда следует важный вывод — только путем сговора, тайного или открытого, продавцы могут добиться наиболее прибыльного для себя результата, который представляет квадрат А. Отсюда становится ясно, насколько важно для общества отсутствие барьеров для вступления в конкурентную борьбу как можно большего числа конкурентов-продавцов, в том числе и иностранных. Теория игр была разработана Джоном Нейманом и Оскаром Моргенштерном в их книге «Теория игр и экономического поведения», вышедшей в 1944 году («The Theory of Games and Economic Behavior», 1944).

Представление игр.

Игры представляют собой строго определённые математические объекты. Игра образуется игроками, набором стратегий для каждого игрока и указания выигрышей, или платежей, игроков для каждой комбинации стратегий. Большинство кооперативных игр описываются характеристической функцией, в то время как для остальных видов чаще используют нормальную или экстенсивную форму.

Игры в экстенсивной, или расширенной, форме представляются в виде ориентированного дерева, где каждая вершина соответствует ситуации выбора игроком своей стратегии. Каждому игроку сопоставлен целый уровень вершин. Платежи записываются внизу дерева, под каждой листовой вершиной.

На рисунке слева — игра для двух игроков. Игрок 1 ходит первым и выбирает стратегию F или U. Игрок 2 анализирует свою позицию и решает — выбрать стратегию A или R. Скорее всего первый игрок выберет U, а второй — A (для каждого из них это оптимальные стратегии); тогда они получат соответственно 8 и 2 очка.

Экстенсивная форма очень наглядна, с её помощью особенно удобно представлять игры с более чем двумя игроками и игры с последовательными ходами. Если же участники делают одновременные ходы, то соответствующие вершины либо соединяются пунктиром, либо обводятся сплошной линией.

В нормальной, или стратегической, форме игра описывается платёжной матрицей. Каждая сторона (точнее, измерение) матрицы — это игрок, строки определяют стратегии первого игрока, а столбцы — второго. На пересечении двух стратегий можно увидеть выигрыши, которые получат игроки. В примере справа, если игрок 1 выбирает первую стратегию, а второй игрок — вторую стратегию, то на пересечении мы видим (−1, −1), это значит, что в результате хода оба игрока потеряли по одному очку.

Игроки выбирали стратегии с максимальным для себя результатом, но проиграли, из-за незнания хода другого игрока. Обычно в нормальной форме представляются игры, в которых ходы делаются одновременно, или хотя бы полагается, что все игроки не знают о том, что делают другие участники.

Применение теории игр.

Теория игр, как один из подходов в прикладной математике, применяется для изучения поведения человека и животных в различных ситуациях. Первоначально теория игр начала развиваться в рамках экономической науки, позволив понять и объяснить поведение экономических агентов в различных ситуациях. Позднее область применения теории игр была расширена на другие социальные науки; в настоящее время теория игр используется для объяснения поведения людей в политологии, социологии и психологии. Теоретико-игровой анализ был впервые использован для описания поведения животных Рональдом Фишером в 30-х годах XX века (хотя даже Чарльз Дарвин использовал идеи теории игр без формального обоснования). В работе Рональда Фишера не появляется термин "теория игр". Тем не менее, работа по существу выполнена в русле теоретико-игрового анализа. Разработки, сделанные в экономике, была применены Джоном Майнардом Смитом в книге "Эволюция и теория игр". Теория игр используется не только для предсказания и объяснения поведения; были предприняты попытки использовать теорию игр для разработки теорий этичного или эталонного поведения. Экономисты и философы применяли теорию игр для лучшего понимания хорошего (достойного) поведения. Вообще говоря, первые теоретико-игровые аргументы, объясняющие правильное поведения, высказывались еще Платоном.

Первоначально теория игр использовалась для описания и моделирования поведения человеческих популяций. Некоторые исследователи считают, что с помощью определения равновесия в соответствующих играх они могут предсказать поведение человеческих популяций в ситуации реальной конфронтации. Такой подход к теории игр в последнее время подвергается критике по нескольким причинам. Во-первых, предположения, используемые при моделировании, зачастую нарушаются в реальной жизни. Исследователи могут предполагать, что игроки выбирают поведения, максимизирующее их суммарную выгоду (модель экономического человека), однако на практике человеческое поведение часто не соответствует этой предпосылке. Существует множество объяснений этого феномена - нерациональность, моделирование обсуждения, и даже различные мотивы игроков (включая альтруизм). Авторы теоретико-игровых моделей возражают на это, говоря, что их предположения аналогичны подобным предположениям в физике. Поэтому даже если их предположения не всегда выполняются, теория игр может использовать как разумная идеальная модель, по аналогии с такими же моделями в физике. Однако, на теорию игр обрушился новый вал критики, когда в результате экспериментов было выявлено, что люди не следуют равновесным стратегиям на практике. Например, в играх "Сороконожка", "Диктатор" участники часто не используют профиль стратегий, составляющий равновесие по Нешу. Продолжаются споры о значении подобных экспериментов. Согласно другой точке зрения, равновесие по Нешу не является предсказанием ожидаемого поведения, но лишь объясняет, почему популяции, уже находящиеся в равновесии по Нешу, остаются в этом состоянии. Однако вопрос о том, как эти популяции приходят к равновесию Неша, остается открытым. Некоторые исследователи в поисках ответа на этот вопрос переключились на изучение эволюционной теории игр. Модели эволюционной теории игр предполагают ограниченную рациональность или нерациональность игроков. Несмотря на название, эволюционная теория игр занимается не только и не столько вопросами естественного отбора биологических видов. Этот раздел теории игр изучает модели биологической и культурной эволюции, а также модели процесса обучения.

Типы игр. Кооперативные и некооперативные.

Игра называется кооперативной, или коалиционной, если игроки могут объединяться в группы, беря на себя некоторые обязательства перед другими игроками и координируя свои действия. Этим она отличается от некооперативных игр, в которых каждый обязан играть за себя. Развлекательные игры редко являются кооперативными, однако такие механизмы нередки в повседневной жизни.

 Часто предполагают, что кооперативные игры отличаются именно возможностью общения игроков друг с другом. В общем случае это неверно. Существуют игры, где коммуникация разрешена, но игроки преследуют личные цели, и наоборот.

 Из двух типов игр, некооперативные описывают ситуации в мельчайших деталях и выдают более точные результаты. Кооперативные рассматривают процесс игры в целом. Попытки объединить два подхода дали немалые результаты. Так называемая программа Нэша уже нашла решения некоторых кооперативных игр как ситуации равновесия некооперативных игр.

 Гибридные игры включают в себя элементы кооперативных и некооперативных игр. Например, игроки могут образовывать группы, но игра будет вестись в некооперативном стиле. Это значит, что каждый игрок будет преследовать интересы своей группы, вместе с тем стараясь достичь личной выгоды.

Симметричные и несимметричные:

 

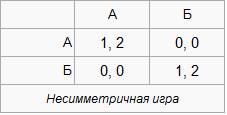
Игра будет симметричной тогда, когда соответствующие стратегии у игроков будут равны, то есть иметь одинаковые платежи. Иначе говоря, если игроки могут поменяться местами и при этом их выигрыши за одни и те же ходы не изменятся. Многие изучаемые игры для двух игроков — симметричные. В частности, таковыми являются: «Дилемма заключённого», «Охота на оленя», «Ястребы и голуби».[7] В качестве несимметричных игр можно привести «Ультиматум» или «Диктатор».

 В примере справа игра на первый взгляд может показаться симметричной из-за похожих стратегий, но это не так — ведь выигрыш второго игрока при профилях стратегий (А, А) и (Б, Б) будет больше, чем у первого.

С нулевой суммой и с ненулевой суммой        :

Игры с нулевой суммой — особая разновидность игр с постоянной суммой, то есть таких, где игроки не могут увеличить или уменьшить имеющиеся ресурсы, или фонд игры. В этом случае сумма всех выигрышей равна сумме всех проигрышей при любом ходе. Посмотрите направо — числа означают платежи игрокам — и их сумма в каждой клетке равна нулю. Примерами таких игр может служить покер, где один выигрывает все ставки других; реверси, где захватываются фишки противника; либо банальное воровство.

Многие изучаемые математиками игры, в том числе уже упоминавшаяся «Дилемма заключённого», иного рода: в играх с ненулевой суммой выигрыш какого-то игрока не обязательно означает проигрыш другого, и наоборот. Исход такой игры может быть меньше или больше нуля. Такие игры могут быть преобразованы к нулевой сумме — это делается введением фиктивного игрока, который «присваивает себе» излишек или восполняет недостаток средств.

Ещё игрой с отличной от нуля суммой является торговля, где каждый участник извлекает выгоду. Сюда также относятся го, шашки, шахматы; в двух последних игрок может превратить свою рядовую фигуру в более сильную, получив преимущество. Во всех этих случаях сумма игры увеличивается. Широко известным примером, где она уменьшается, является война.

Классификация игр.

Различные виды игр можно классифицировать, основываясь на том или ином принципе: по числу игроков, по числу стратегий, по свойствам функций выигрыша, по возможности предварительных переговоров и взаимодействия между игроками в ходе игры.

Дадим формальное описание перечисленных элементов конфликта. Множество всех игроков, обозначаемое I, в случае конечного их числа может задаваться простым перечислением игроков. Например, I = {1, 2} при игре в орлянку, I = {Продавец, Покупатель} в ситуации монополия-монопсония, I = {1, 2, ..., n} в случае анализа результатов голосования в парламенте.

Множество стратегий игрока i обозначим через Xi. При игре в орлянку каждый игрок располагает двумя стратегиями: Xi = {Орел, Решка}; каждый участник голосования имеет выбор на множестве стратегий {За, Против}. В случае взаимодействия на рынке как Продавец, так и Покупатель могут назначать некоторую неотрицательную цену на продаваемый (покупаемый) товар, т.е. множество стратегий каждого из них Xi: Рi > 0.

В каждой партии игрок выбирает некоторую свою стратегию xi Xi , в результате чего складывается набор стратегий x = {x1, x2, ..., xn}, называемый ситуацией. Так, ситуацию в Парламенте описывает список {За, За, Против, За, ...}, полученный в итоге проведенного голосования.

Заинтересованность игроков в ситуациях проявляется в том, что каждому игроку i в каждой ситуации х приписывается число, выражающее степень удовлетворения его интересов в данной ситуации. Это число называется выигрышем игрока i и обозначается через hi(x), а соответствие между набором ситуаций и выигрышем игрока i называется функцией выигрыша (платежной функцией) этого игрока Нi.

В случае конечной игры двух лиц функции выигрыша каждого из игроков удобно представлять в виде матрицы выигрышей, где строки представляют стратегии одного игрока, столбцы - стратегии другого игрока, а в клетках матрицы указываются выигрыши каждого из игроков в каждой из образующихся ситуаций. Данная форма представления конечных игр двух лиц объясняет общее для них название - матричные игры.

Например, в случае игры в орлянку каждый из игроков имеет по две стратегии, именуемые Орел и Решка. Если игроки выбирают одинаковые стратегии, т.е. в случаях, если оба говорят «Орел» или оба говорят «Решка», 1-й игрок выигрывает 1 рубль, а второй игрок проигрывает 1 рубль. В ситуациях, когда оба игрока выбирают различные стратегии, 1_й игрок проигрывает 1 рубль, а 2_й игрок соответственно этот 1 рубль выигрывает.

В итоге матрица выигрышей 1_го игрока Н1 выглядит следующим образом:

Стратегии 2-го игрока:                       

|Орел Решка|                                           

Стратегии 1-го игрока:

|Орел Решка|                                                     

Соответственно матрица выигрышей 2_го игрока Н2 имеет вид:

Стратегии 2-го игрока                        

|Орел Решка|                                           

Стратегии 1-го игрока                        

|Орел Решка|

Приведем пример записи функции выигрыша для бесконечной игры. В случае дуополии каждый из игроков может объявить цену р, по которой он хотел бы продать некоторое количество товара. При этом предполагается, что потребители приобретут товар у фирмы, объявившей меньшую цену, или распределяет свой спрос поровну между фирмами в случае, если они назначили одинаковую цену. Если функцию спроса в зависимости от цены на товар обозначить как d(p), то функция выигрыша 1_й фирмы П1(р1, р2) будет иметь вид:

{ р1d(p1), если p1 < p2,

П1(р1, р2) = { если p1 = p2,

{ 0, если p1 > p2.

Аналогично выглядит функция выигрыша 2-й фирмы П2(р1, р2).

Оценка эффективности стратегий. Принцип гарантированного результата.

Оценка эффективности стратегий в случае условия может базироваться на известных леммах типа леммы Неймана-Пирсона. Эти леммы будут приведены далее. По существу некоторые из этих результатов ранее были получены А. А. Ляпуновым, но в менее подходящей трактовке.

Оценка эффективности стратегий является сравнительно простой задачей для расчетов, только если законы распределения случайных факторов известны достаточно точно и, кроме случайных факторов, других неконтролируемых факторов нет. Во всех остальных случаях оценка эффективности требует решения задач на отыскание глобального минимума.

При данном критерии эффективности оценка эффективности стратегий (и выбор из них) должна происходить на основе получения гарантированной (максимальной гарантированной) величины критерия эффективности при данной информированности исследователя операции и предполагающейся при формировании рассматриваемых стратегий информированности оперирующей стороны об обстановке операции.

Чистый дисконтированный доход - главный критерий оценки эффективности стратегии - определяется на основе денежных потоков как сумма за весь расчетный период приведенных к базовому (начальному) моменту времени величин чистого дохода (разностей стоимостных оценок результатов и затрат) в каждом интервале времени.

Для достижения этой цели необходимо обеспечить максимальную экономичность и надежность системы энергоснабжения, а также экономию энергии во всех сферах ее использования, в том числе и в ТЭК, на основе ускорения научно-технического прогресса. В качестве критерия оценки эффективности планируемой стратегии при этом может быть использован показатель удельной энергоемкости общественного валового продукта или национального дохода.

Оценка эффективности стратегий и выбор из них осуществляются исследователем операций на основе получения максимально гарантированной величины критерия эффективности при предполагающейся информированности оперирующей стороны о неконтролируемых факторах. Если 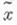 - стратегия оперирующей стороны, то ее оценкой, когда известно лишь, что  называется величина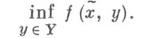

Принцип гарантированного результата в терминах теории исследования операций сформулирован следующим образом: при данном показателе эффективности оценка эффективности стратегий (и выбор из них) должна происходить на основе получения гарантированной (максимально гарантированной) величины показателя эффективности при данной информированности исследователя операции и предполагающейся при формировании рассматриваемых стратегий информированности оперирующей стороны об обстановке операций.

Исследование операций, т. е. совокупности действий, ведущих к достижению поставленной цели, проводится исследователем операции в интересах оперирующей стороны, которая стремится к достижению цели, математически выражаемой желанием увеличить критерий эффективности – функцию 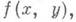 где  - выбор оперирующей стороны, 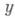 - неконтролируемый оперирующей стороной фактор. Выбор конкретных значений  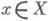в зависимости от информированности оперирующей стороны и исследователя операции о значениях определяет стратегию  оперирующей стороны.

Наибольший гарантированный результат  определяется как величина

Стратегия , для которой 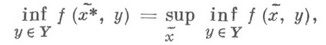 является оптимальной в рассматриваемой операции.

Принцип гарантированного результата – принцип, используемый участниками, которые не хотят рисковать, а желают получить гарантированный результат. То есть при любом ходе, при любом варианте надо получить гарантированный результат независимо от действий другого игрока. Оптимальное решение : e* = maxi minj eij  сначала для гарантии соглашаемся с наименьшим результатом, но затем от части компенсируем это, выбирая решение, для которого гарантированный результат максимален.

Примеры оценки эффективности и гарантированного результата.

Формирование представления о лучшей стратегии  стороны P1 предполагает либо возможность определения лучшего варианта для любой пары стратегий, этой стороны, либо возможность установления равноценности стратегий, входящих в эту пару. Однако на множестве стратегий стороны P1 не существует отношения предпочтения, позволяющего ответить на эти вопросы для любой пары.

Проиллюстрируем это важное обстоятельство путем сравнения уровней эффективности, обеспечиваемых соответственно стратегиями x1=0 и x1=1.

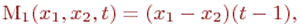                                        (2.1)

откуда вытекает, что

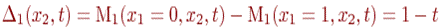               (2.2)

и, следовательно,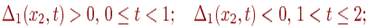 

и,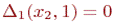

Таким образом, при неизвестном состоянии природы стратегии x1=0 и x1=1 оказываются несравнимыми.

Рис. 1.2

Следовательно, введенная в модели упорядоченность всех исходов операции, с помощью которой мы описали интересы первой стороны, не порождает полного отношения предпочтений на множестве стратегий этой стороны. Причина состоит в том, что неопределенность значения параметра t вызывает неопределенность самого исхода. Поэтому возможность оценки эффективности конкретной стратегии, которая необходима для определения наилучшего выбора, оказывается фундаментально связанной с информированностью стороны о состоянии природы и (в общем случае) о действиях другой стороны.

Как следует из предшествующего рассмотрения, для обеспечения сравнимости стратегий принципиально необходимо принять некоторую гипотезу о неизвестном состоянии природы. В рассматриваемом примере вся имеющаяся у стороны P1 информация о сроке t проведения конкурса сводится к знанию интервала [0, 2], заведомо содержащего этот неизвестный срок. В связи с указанной неопределенностью состояния природы, в качестве оценки эффективности любой стратегии можно принять тот уровень эффективности, который гарантируется использованием этой стратегии.

Принятие такой оценки в качестве прогноза результатов планируемых действий является рекомендацией, основанной на обширном опыте принятия решений в практической деятельности. К этому "правилу худшего случая" приходят многочисленные исследователи опыта принятия решений, относящегося к самым различным областям человеческой деятельности. Приведем несколько примеров.

Известный американский специалист в области создания больших программных систем Ф.П. Брукс отмечает, что "наши методы оценки весьма несовершенны. Строго говоря, они отражают некоторое неявно высказываемое и в корне неверное допущение, что все будет идти хорошо, ... выполнение каждого задания займет ровно столько времени, сколько оно "должно" занять". И далее: "Планируйте неудачу: она вас, так или иначе, найдет 1 ".

Можно даже говорить о возникновении своего рода "фольклора", вызванного к жизни необходимостью ориентации на худший случай в практике принятия решений. К числу таких новых жанров относятся, например, так называемые "законы Мэрфи 2 ":

Все сложнее, чем кажется.

Все тянется дольше, чем можно ожидать.

Все оказывается дороже, чем планировалось.

Если что-то может испортиться, оно обязательно испортится.

По поводу этих законов некто Каллаген сделал следующее замечание 3 "Мэрфи был оптимистом". Действительно, например, второй из "законов" неявно предполагает, что планируемая работа, в конце концов, все-таки завершится. Но этого успешного завершения может и не быть. В книге Дж.Фокса 4 сообщается, что "военно-воздушные силы США затратили более 300 млн. долларов на тщетную попытку автоматизировать комплексную систему перевозок и снабжения".

Вернемся к рассматриваемому примеру и построим оценку эффективности, которую гарантирует стратегия x1 стороны P1 при неизвестном сроке t проведения конкурса. Эта оценка худшего случая, очевидно, определяется величиной

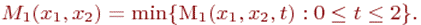                            (2.3)

Подставляя в (2.3) правую часть выражения (2.1) для функции, 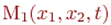 приводим оценку (2.3) к виду

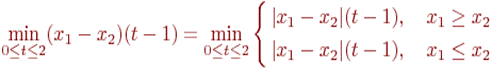              (2.4)

Теперь из (2.3), (2.4) следует, что

                                                                    (2.5)

причем эта гарантированная величина реализуется либо в случае проведения конкурса в момент t*=0, либо в случае проведения этого конкурса в момент t*=2.

Первый случай соответствует ситуации, когда, 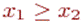 а второй - ситуации, когда,  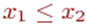  т.е.

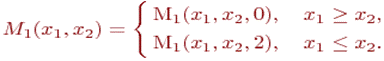                                       (2.6)

Теперь проведем аналогичное рассмотрение, руководствуясь интересами второй стороны. Определим уровень эффективности, который может быть обеспечен стороне P2 выбором стратегии x2 при некоторой известной стратегии x1 первой стороны и неизвестном сроке проведения конкурса, т.е. вычислим величину

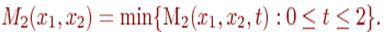                                        (2.7)

Из (1.20), (2.1) и (2.7) следует, что           (2.8)

При этом справедливо следующее соотношение, являющееся аналогом выражения (2.6)

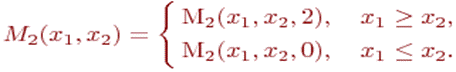                         (2.9)

Таким образом, согласно (2.5) и (2.8),

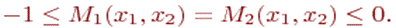                                     (2.10)

Следовательно, при ориентации обеих сторон на худший случай (т.е. при использовании ими оценок гарантированного уровня эффективности) противоположность интересов сторон, характеризуемая нулевой суммой критериев (1.21), сменяется ситуацией полного совпадения интересов.

Список используемой литературы.

1.     Источник: http://ru.wikipedia.org/wiki....3%D1%80

2.     «Теория игр и экономическое поведение» 1944 г. монография Дж. Неймана и О. Моргенштерна.

3.     Теория игр для экономистов» вводный курс»; Печерский С.Л.; Беляева А.А.

4.     «Теория игр с примерами из математической экономики»; 1985; 

           Мулен, Эрве Москва.

     5.  http://dic.academic.ru/dic.nsf/enc_mathematics/3294/.

Список используемой литературы.

1.     «Теория игр и экономическое поведение» 1944 г. монография Дж. Неймана и О. Моргенштерна.

2.     Теория игр для экономистов» вводный курс»; Печерский С.Л.; Беляева А.А.

3.     «Теория игр с примерами из математической экономики»; 1985; 

           Мулен, Эрве Москва.

     4.  http://dic.academic.ru/dic.nsf/enc_mathematics/3294/.