Ограниченность

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ «РОССИЙСКИЙ ГОСУДРАТСВЕННЫЙ ПЕДАГОГИЧЕСКИЙ УНИВЕРСИТЕТ ИМ А.И. ГЕРЦЕНА»

Институт педагогики и психологии

Кафедра социальной педагогики

РЕФЕРАТ

По теме:

«Ограниченность»

Студентки дневного отделения

1 курса группы 15-60

Поляковой Валерии Николаевны,

обучающейся по направлению

040400.62 – «Социальная работа»,

профиль «Социальная защита и социальное

обслуживание семей и детей»

Санкт-Петербург

2016

В математическом анализе, и прилегающих разделах математики, ограниченное множество — множество, которое в определенном смысле имеет конечный размер. Базовым является понятие ограниченности числового множества, которое обобщается на случай произвольного метрического пространства, а также на случай произвольного частично упорядоченного множества. Понятие ограниченности множества не имеет смысла в общих топологических пространствах, без метрики.

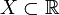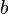Множество вещественных чисел  называется ограниченным сверху, если существует число , такое что все элементы 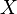 не превосходят b:

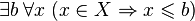
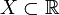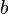Множество вещественных чисел  называется ограниченным снизу, если существует число , такое что все элементы 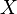 не меньше b: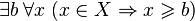 

Множество 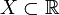, ограниченное сверху и снизу, называется ограниченным.

Множество 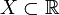, не являющееся ограниченным, называется неограниченным. Как следует из определения, множество не ограничено тогда и только тогда, когда оно не ограничено сверху или не ограничено снизу.

Примером ограниченного множества является отрезок ,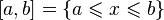

-неограниченного — множество всех целых чисел ,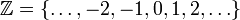

-ограниченного сверху, но неограниченного снизу — луч ,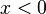

-ограниченного снизу, но неограниченного сверху — луч .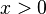

Функция f называется ограниченной на множестве E, если найдется такое число M>0, что для любого x∈E справедлива оценка |f(x)|

Функция f называется ограниченной сверху на множестве E, если найдется такое число M, что для любого x∈E справедлива оценка f(x)

Функция f называется ограниченной снизу на множестве E, если найдется такое число m, что для любого x∈E справедлива оценка f(x)>m.

Примеры:

Функция f(x)=sinx  ограничена при всех x∈R.

Функция f(x)=|x|  ограничена снизу при всех x∈R.

Функция f(x)=1/x  ограничена сверху при x∈[−∞;0).

Функция, ограниченная сверху.

Графически ограниченность сверху означает, что существует такая прямая y=b, выше которой нет точек графика функции y=f(x).

Число b называется верхней границей функции y=f(x) на множестве X.

Функция, ограниченная снизу.

Число a называется нижней границей функции f(x) на множестве XX.

Графически ограниченность снизу означает существование такой прямой y=a, ниже которой нет точек графика функции y=f(x).

Функция, ограниченная на множестве.

Определение: число M называется верхней гранью фунции y=f(x) на множестве X, если выполнены следующие условия:

1) ∀x∈X(f(x)≤M),

2) ∀ε>0∃x′(f(x′)>M−ε).

M=supx∈Xf(x).

Число m назвается нижней гранью функции y=f(x) на множестве X, если выполнены условия:

1) ∀x∈X(f(x)≥m),

2) ∀ε>0∃x′′∈X(f(x′′)

m=infx∈Xf(x).

M=supx∈Xf(x) назыается локально наибольшим значением, если X⊂D(f) и глобально наибольшим значением, если X=D(f).

m=infx∈Xf(x) назыается локально наименьшим значением, если X⊂D(f) и глобально наименьшим значением, если X=D(f).

Функция y=f(x) называется неограниченной на множестве X, если ∃c>0∀x∈X(|f(x)≤c|)≡∀c>0∃x∈X(|f(x)|>c).