О СВЯЗИ РАДИАЛЬНЫХ И ВЕРТИКАЛЬНЫХ КОЛЕБАНИЙ ЧАСТИЦ В ЦИКЛИЧЕСКИХ УСКОРИТЕЛЯХ

Министерство образования и науки Российской Федерации

Федеральное государственное автономное образовательное учреждение высшего профессионального образования

"Уральский федеральный университет

имени первого Президента России Б.Н. Ельцина"

О СВЯЗИ РАДИАЛЬНЫХ И ВЕРТИКАЛЬНЫХ КОЛЕБАНИЙ ЧАСТИЦ В ЦИКЛИЧЕСКИХ УСКОРИТЕЛЯХ

Реферат

студентки 4 курса

ИМКН гр. МХ-401

Теличкиной О.Н.

Преподаватель

Долгий Ю.Ф.

Екатеринбург

2016

            В настоящем реферате определяются чисторадиальные колебания и исследуется их устойчивость. Затем проводится преобразование уравнений колебаний, и по методу малого параметра Пуанкаре находятся вертикально-радиальные колебания. Существует единственное значение определяющего физического параметра, при котором имеется единственная приведённая амплитуда вертикально-радиальных колебаний, а чисторадиальные колебания при этом значении параметра неустойчивы для сколь угодно малой их амплитуды. Далее описывается переходный процесс и определяется время перехода чисторадиальных колебаний в вертикально-радиальные, а затем отмечается аналогия с пружинным маятников, в частности, в переходных процессах.

            1. Первый этап.

Уравнения бетатронных колебаний частиц в циклических ускорителях со слабой фокусировкой имеют вид:

                           ,             .     (1)

Здесь 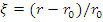 ,  ; r и z — две из цилиндрических координат частицы, точка сверху обозначает дифференцирование по времени; константы ω, n и k есть:

где m и e — масса и заряд частицы, c — скорость света,  — вертикальная компонента вектора напряжённости магнитного поля, значения частных производных вычислены при  — радиусе траектории, соответствующем заданной величине энергии частиц.

Введём безразмерное время    и запишем систему (1) в виде

где положительные параметры α и β суть

Предполагаем, что система (1) допускает первый интеграл вида

где W — квадратичная форма, а S₃ означает совокупность членов не ниже третьего порядка.

Для системы (3) этот интеграл есть интеграл энергии частиц, соответствующий колебательной  части движения

Прежде чем приступить к преобразованию системы (3), заметим, что она допускает решение (чисторадиальные колебания частиц)

Из интеграла (5) следует, что константа μ² равна квадрату амплитуды чисторадиальных колебаний. Для суждения об устойчивости последних положим в (3)

и получим уравнения в вариациях в виде

Отсюда следует, что неустойчивость чисторадиальных колебаний (6) определяется неустойчивостью тривиального решения второго из последних уравнений — уравнения Матье. Физически определяющим параметром является n (из (2)). Области неустойчивости на плоскости μn примыкают к критическим точкам на оси n, определяемым равенствами

откуда

Широкая область неустойчивости (т.е. с отличным от нуля углом между касательными) примыкает лишь к точке , тангенс угла наклона касательных определяется формулой

Таким образом, в первом приближении единственная широкая область неустойчивости (6) в плоскости μn определяется неравенствами

с критическим значением  .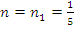

            2. Второй этап.

Перейдём теперь к преобразованию системы (3). По формулам

)

     (χ = 1, ..., k) ,

найдём

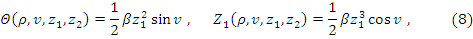
Уравнение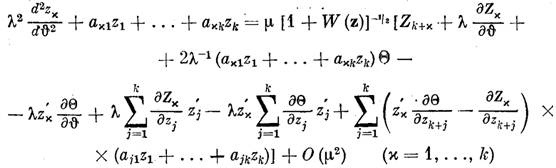

запишется в виде ( )

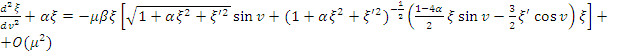.      (9)

Уравнение (9) при  и 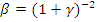 переходит в уравнение (3*):

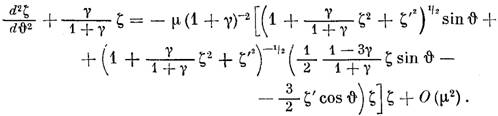
Возникает вопрос об определении периодических решений этого уравнения. Применим метод малого параметра для неавтономных систем с одной степенью свободы в форме, предложенной Пуанкаре. Будем искать это решение в виде ряда

и, подставляя этот ряд в уравнение (3*) , получим уравнения для нахождения  и

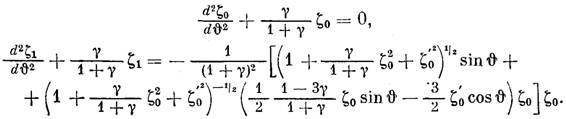
Первое из них обладает семейством 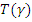-периодических решений

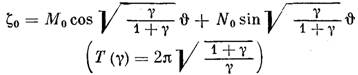(4*)

Решение (4*) можно рассматривать и как -периодическое, где q — любое натуральное число. Уравнение (3*) зависит явно от независимой переменной v, и эту зависимость также можно рассматривать как -периодическую с любым натуральным p. Поэтому решение (4*) будет порождающим для -периодического решения уравнения (3*) тогда и только тогда, когда

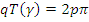   или  ,

где  — любая несократимая неправильная дробь.

Отсюда получаем, что уравнение (9) допускает периодические решения с наименьшим периодом  (p = 1, 2, ...) только лишь для значений , то есть, в силу (4), для

где q и p — любые взаимно простые числа. Множество значений n, определяемое формулой (10), всюду плотно на интервале (0, 1) изменения n, иначе говоря, каждое значение  либо определяется формулой (10), либо может быть представлено ею с любой степенью точности. При всех значениях n в (10), кроме , формула (4*) доставит семейство порождающих решений уравнения (9) от двух параметров.

Остановимся в заключение на значении  — единственном значении n, при котором порождающее решение уравнения (9) имеет вид   , и для которого чисторадиальные колебания (6) неустойчивы при сколь угодно малой их амплитуде μ.

По формулам

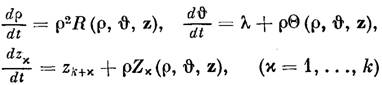
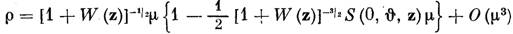
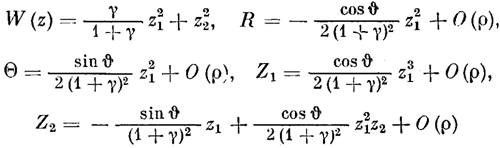
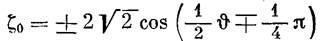
получим

Отсюда будем иметь для периода вертикально-радиальных колебаний при

а для закона движения будем иметь

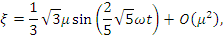
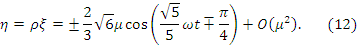
Величина 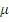 определяется по начальному значению приведённой энергии (5) колебаний.

            3. Третий этап.

Перейдём к описанию процесса перекачки энергии при , т.е. переходного процесса от неустойчивых чисторадиальных колебаний (6) к вертикально-радиальным колебаниям (12). Укороченные уравнения Ван-дер Поля будут иметь вид

Определим закон изменения амплитуды Ван-дер Поля. Разделим первое из уравнений (1*) на второе

и поделим результат на

Далее разделим переменные

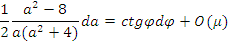
и интегрируем:

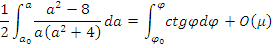
результатом интегрирования является выражение

Домножаем (2*) на 2 и переносим все константы перед логарифмами в степени

и объединяем по свойствам логарифма

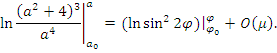
Затем подставим пределы интегрирования

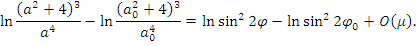
Объединяем логарифмы по свойствам и потенцируем

полученный результат домножаем на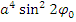  

и находим первый интеграл укороченных уравнений Ван-дер Поля:

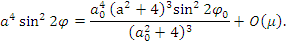
Однако, подстановка этого интеграла в первое из уравнений (1*) приводит к необозримым квадратурам. Впрочем, укороченные уравнения Ван-дер Поля, разумеется, дают лишь первое приближение решения уравнения (9) (дальнейшие приближения определяются по методу последовательных приближений Пикара и вытекающими из него оценками точности). Поэтому мы ограничимся приближенным интегрированием системы (1*). Из второго уравнения (1*) следует, что при  имеем  и будем иметь 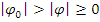. Поскольку при  в силу подстановки Ван-дер Поля имеем , где, напомним,  есть амплитуда порождающего решения, то на весь промежуток процесса срыва (перехода вертикальных колебаний в маятниковые качания) можно положить , если  достаточно мало.

Тогда первое уравнение (1*) даст нам для

и после интегрирования найдём

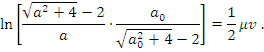
Отсюда получим приближенный закон изменения амплитуды Ван-дер Поля

Время 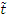 переходного процесса от чисторадиальных колебаний (6) к вертикально-радиальным (12) при  определится из формулы

где

а величина 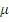 определяется по начальному значению приведённой энергии колебаний (5).