Федеральное агентство по образованию
ГУ ВПО
ВСЕРОССИЙСКИЙ ЗАОЧНЫЙ
ФИНАНСОВО-ЭКОНОМИЧЕСКИЙ ИНСТИТУТ
Кафедра математика и информатика
КОНТРОЛЬНАЯ РАБОТА
Дисциплина: Финансовая математика
вариант № 3
Выполнил студент
Группа № 4ф2ДО
Студенческий билет №06ДФД50396
Проверил: Копылов Юрий Николаевич
Барнаул 2008г
СОДЕРЖАНИЕ
| Задача №1 |
| Задача №2 |
| Задача №3 |
Задача №1
Приведены по квартальные данные о кредитах от коммерческого банка на жилищное строительство (в условных единицах) за 4 года.
| 1 | 31 |
| 2 | 40 |
| 3 | 47 |
| 4 | 31 |
| 5 | 34 |
| 6 | 44 |
| 7 | 54 |
| 8 | 33 |
| 9 | 37 |
| 10 | 48 |
| 11 | 57 |
| 12 | 35 |
| 13 | 42 |
| 14 | 52 |
| 15 | 62 |
| 16 | 39 |
Требуется:
Построить адаптивную мультипликативную модель Хольта – Уинтерса с учетом сезонного фактора, приняв параметры сглаживания а1=0,3, а2=0,6, а3=0,3
Оценить точность построенной модели с использованием средней относительной ошибке аппроксимации.
Оценить адекватность построенной модели с использованием средней относительной по критерию типов:
- независимости уровней ряда остатков по d-критерию (критические значения d1=1.10, d2=1.37, и по первому коэффициенту автокорреляции при критическом значении r=0.32
- нормальности распределения остаточной компоненты по R/S критерию с критическими значениями от 3 до 4,21
4) Построить точечный прогноз на 4 шага вперед т.е. на 1 год
5) Отразить на графике фактические и расчетные данные.
Решение:
| t | Y(t) | Yp(t) |
| 1 | 31 | 36,00 |
| 2 | 40 | 36,93 |
| 3 | 47 | 37,86 |
| 4 | 31 | 38,79 |
| 5 | 34 | 39,71 |
| 6 | 44 | 40,64 |
| 7 | 54 | 41,57 |
| 8 | 33 | 42,50 |
| линейнная | b(0) | a(0) |
| 0,9286 | 35,0714 |
| a1 | 0,3 |
| aF | 0,6 |
| a3 | 0,3 |
| t | Y(t) | a(t) | b(t) | F(t) | Yp(t) | e(t) =Y-Yp | e(t) ^2 | пов. Точки |
| -3 | 0,859 | |||||||
| -2 | 1,083 | |||||||
| -1 | 1,049 | |||||||
| 0 | 35,071 | 0,929 | 0,788 | |||||
| 1 | 31 | 36,310 | 1,022 | 0,856 | 30,91 | 0,09 | 0,01 | 0 |
| 2 | 40 | 37,520 | 1,078 | 1,073 | 40,43 | -0,43 | 0,18 | 1 |
| 3 | 47 | 40,786 | 1,734 | 1,111 | 40,48 | 6,52 | 42,48 | 1 |
| 4 | 31 | 42,089 | 1,605 | 0,757 | 33,50 | -2,50 | 6,25 | 0 |
| 5 | 34 | 42,987 | 1,393 | 0,817 | 37,39 | -3,39 | 11,48 | 0 |
| 6 | 44 | 43,788 | 1,215 | 1,032 | 47,61 | -3,61 | 13,04 | 1 |
| 7 | 54 | 46,449 | 1,649 | 1,142 | 50,00 | 4,00 | 16,03 | 1 |
| 8 | 33 | 47,240 | 1,392 | 0,722 | 36,41 | -3,41 | 11,65 | 1 |
| 9 | 37 | 48,049 | 1,217 | 0,789 | 39,72 | -2,72 | 7,42 | 0 |
| 10 | 48 | 48,804 | 1,078 | 1,003 | 50,84 | -2,84 | 8,09 | 1 |
| 11 | 57 | 50,216 | 1,178 | 1,138 | 56,96 | 0,04 | 0,00 | 1 |
| 12 | 35 | 50,873 | 1,022 | 0,702 | 37,10 | -2,10 | 4,43 | 1 |
| 13 | 42 | 52,608 | 1,236 | 0,795 | 40,93 | 1,07 | 1,14 | 1 |
| 14 | 52 | 53,616 | 1,167 | 0,983 | 54,00 | -2,00 | 4,00 | 1 |
| 15 | 62 | 55,045 | 1,246 | 1,131 | 62,33 | -0,33 | 0,11 | 1 |
| 16 | 39 | 56,455 | 1,295 | 0,695 | 39,49 | -0,49 | 0,24 | 0 |
| Сумма | 126,57 | 11 | ||||||
| среднее | -0,758 | |||||||
| (et-et-1) ^2 | et*et-1 | модуль(e(t) /Y(t)) *100 |
| 0,01 | 0,000 | 0,290 |
| 0,27 | -0,038 | 1,065 |
| 48,21 | -2,776 | 13,868 |
| 81,33 | -16,297 | 8,066 |
| 0,79 | 8,473 | 9,966 |
| 0,05 | 12,238 | 8, 208 |
| 57,99 | -14,460 | 7,415 |
| 55,02 | -13,669 | 10,345 |
| 0,48 | 9,302 | 7,364 |
| 0,01 | 7,748 | 5,924 |
| 8,31 | -0,110 | 0,068 |
| 4,60 | -0,082 | 6,014 |
| 10,06 | -2,245 | 2,540 |
| 9,41 | -2,134 | 3,848 |
| 2,78 | 0,667 | 0,538 |
| 0,03 | 0,164 | 1,263 |
| 279,34 | -13,221 | |
| 5,42 |
Получили что средняя ошибка аппроксимации равна 5,42 - меньше 15%, то есть точность модели удовлетворительная
| Se= | 2,905 |
Критерий Поворотных точек
p=11
| критическое по формуле | 6 |
Поскольку число поворотных точек больше критического то критерий поворотных точек выполняется
3) критерий Дарбина – Уотсона
| d= | 2,21 |
| d1= | 1,10 |
| d2= | 1,37 |
варианты
1) если d меньше d1 - критерий не выполняется
2) если d больше d1 и меньше d2 - рассчитываем r1
3) если d больше d2, но меньше 2 - критерий выполняется
4) если d больше 2, то вычисляем 4-d и его проверяем
4-d=4-2,21=1,79
так как 1,10<1,79<1,37, то условие независимости ряда остатков выполняется.
Применим 2 вариант критерия, расчитываем r1
В таб доп. Колонка для расчета r1 с названием et*et-1
| r1 = | -0,10 |
| r таб= | 0,32 |
вывод поскольку r1 4) R/S критерий Так как 3<3,49<4,21, то
уровни остатков подчиняются нормальному распределению. ОБЩИЙ ВЫВОД: модель адекватна и
подходит для расчета прогнозных значений Даны цены (открытия
максимальная, минимальная и закрытия) за 10 дней. Интервал сглаживания принять
равным 5 дням. Рассчитать: - экономическую скользящую
среднюю; - момент; - скорость из изменения цен; - индекс относительной силы; -%R,%K и%D 1 2 3 4 5 6 7 8 9 10 735 750 745 725 738 747 835 875 853 820 701 715 715 707 702 716 755 812 821 760 715 738 720 712 723 744 835 827 838 767 Решение: n=5 –
интервал сглаживания Подставляя данные в эти формулы
получаем повышение Общий вывод по этому показателю:
в 10 день кривые сблизились, причем дневная сверху - приготовится к продаже, но
поскольку имеются колебания в последние дни нужно быть осторожным Вывод: у нас в
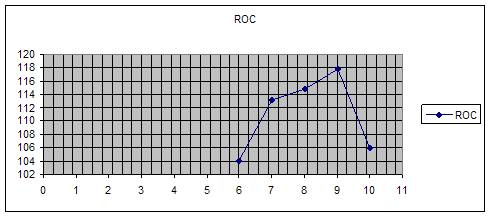
6,7 день ниже 100 - снижение цены, предпочтительнее продажа 8,9 - повышение
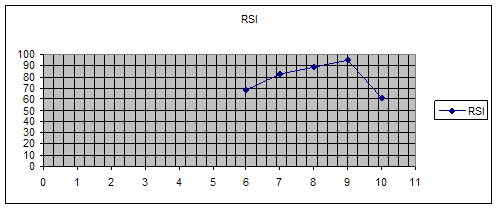
цены, покупка, а в 10 день - продажа так как ниже 100% Вывод: у нас все значения выше
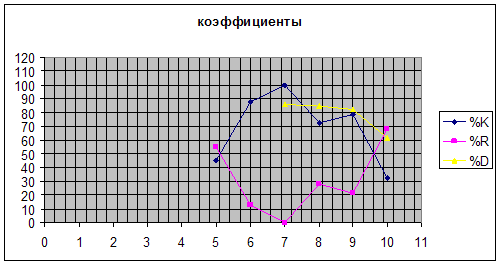
100 - повышение цены, предпочтительнее покупка. Вывод: 6 день выходит из зоны - покупка,
7,8,9 день - подготовится к продаже, 10 день выходит из зоны – покупать По линии K%: В 5 день критерий находится в
зоне перепроданности подготовится к покупке, в 6,7 находится в зоне
перекупленности подготовится к продаже на 8,9 день выходит из зоны
перекупленности покупке; 10 день показывает что надо покупать. По линии R%: В 5 день вышел из зоны
перепроданности надо покупать, 6.7.9. - (в зоне перепроданности) - подготовиться
к покупке, 10 день вышел из зоны надо покупать. По линии D%: 10 день показал что нужно
покупать Найти: 3.1.1. Точные проценты с точным
числом дней ссуды; 3.1.2. Обыкновенные проценты с
точным числом дней ссуды. 3.1.3. Обыкновенные проценты с
приближенным числом дней ссуды Решение: а) вычислить точные проценты с
точным числом дней ссуды б) вычислить обыкновенные
проценты с точным числом дней К= в) вычислить обыкновенные
проценты с приближенным числом дней 3.2) Через
Тдн дней подписания договора должник уплатит S рублей. Кредит выдан под i%
годовых (проценты обыкновенные). Какова первоначальная сумма и дисконт Решение:
Дисконт
– разница между тем, что он отдал и тем, что взял – фактически – это сумму
начисленных процентов. 3.3) Через
Тдн предприятие должно получить по векселю S руб. Банк приобрел этот вексель с
дисконтом. Банк учел вексель по учетной ставке i% годовых (год равен 360 дней).
Определить полученную сумму и дисконт? 3.4) В
кредитном договоре на сумму S руб. и сроком на Тлет, зафиксирована ставка
сложных процентов, равная i% годовых. Определить наращенную сумму? 3.5) Ссуда,
размером S руб. и предназначена сроком на Т лет. Проценты сложные, ставка i%
годовых. Проценты начисляются m раз в году. Вычислить наращиваемую сумму? 3.6) Вычислить
эффективную ставку процента если банк начисляет проценты m раз в году, исходя
из номинальной ставки i% годовых 3.7) Определить
какой должна быть номинальная ставка при начислении процентов m раз в году,
чтобы обеспечить эффективную ставку i% годовых. 3.8) Через
Тлет предприятию будет выплачена сумма S руб. Опрделить ее современную
стоимость при условии, что применяется сложная ставка i% годовых? 3.9) Через
Тлет по векселю должна быть выплачена сумма S руб. Банк учел вексель по сложной
учетной ставке i% годовых. Определить дисконт? S= 3.10) В
течении Тлет на расчетный счет в конце каждого года поступает по S руб., на которые
m раз в году начисляются проценты по сложной годовой ставке i%. Определить
сумму на расчетном счете к концу указанного периода?
e min
e max
-3,61
6,52
Прогноз
17
45,88351001
18
58,04633626
19
68,24039581
20
42,84375034

Задача №2
Дни
Цены
максимальная
минимальная
Закрытия
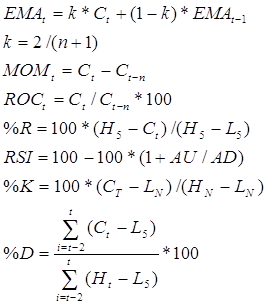
T
H(t)
L(t)
C(t)
EMA(t)
MOM
ROC
Изменения Ci
1
735
701
715
2
750
715
738
23
3
745
715
720
-18
4
725
707
712
-8
5
738
702
723
721,60
11
6
747
716
744
729,06
29
104,06
21
7
835
755
835
764,34
97
113,14
91
8
875
812
827
785, 20
107
114,86
-8
9
853
821
838
802,79
126
117,70
11
10
820
760
767
790,87
44
106,09
-71
понижение
AU
AD
RSI
23
0
0
18
0
8
11
0
21
0
55
26
67,90
91
0
123
26
82,55
0
8
123
16
88,49
11
0
134
8
94,37
0
71
123
79
60,89
H5
L5
H5-L5
Ct-L5
%K
H5-Ct
%R
%D
750
701
49
22
44,90
27
55,10
750
702
48
42
87,50
6
12,50
835
702
133
133
100,00
0
0,00
85,65
875
702
173
125
72,25
48
27,75
84,75
875
702
173
136
78,61
37
21,39
82,25
875
716
159
51
32,08
108
67,92
61,78


Задача №3
Сумма
Дата начальная
Дата конечная
Время в днях
Время в годах
Ставка
Число начислений
S
TH
TK
Тдн
Тлет
i
m
1500000
17,01,02
13,03,02
180
4
20
2
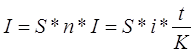
3,1)
сумма процентов
S-сумма кредита
i-ставка за кредит
n - количество периодов начисления (поскольку
проценты годовые, то n = t /K)
t - срок в днях
K - число дней в году
K=
365
S=
1500000
i=
20
t=
56
сумма процентов
46027,40
360
S=
1500000
i=
20
t=
56
сумма процентов
46666,67
число месяца когда взял
число месяца когда отдал
разница
17
13
4
t=
55
K=
360
t=
55
S=
1500000
i=
20
сумма процентов
45833,33
![]()
Первоначальная сумма=
136 364
через Тдн=
180
должник уплатит S=
1500000
процентная ставка i=
20
K=
360
дисконт =
1 363 636

![]()
Дисконт=
150000
t=Тдн=
180
K=
360
S=
1500000
d=i=
20
P=
1350000
P=
15694117,03
n=Тлет=
4
i=
20
S=
1500000
множ. Наращивания=
11,46
![]()
S=
1500000
n=Tлет=
4
m=
2
%i=
20%
P=
3215383,215
![]()
m=
2
%i=
20%
Iэ=
21,55%
0,21550625
21,55063
![]()
m=
2
iэ=
20%
i=
38,2%
0,38178046
38,17805
![]()
S=
1500000
n=Tлет=
4
%i=
20%
P=
602816,36
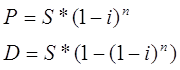
1500000
n=Tлет=
4
%i=
20%
современная сумма=
614400,00
Дисконт=
885600,00
![]()
S=
1500000
n=Tлет=
4
%i=
20%
m=
2
R=
24 194 601













 (zip - application/zip)
(zip - application/zip)










