Матрицы. Операции над матрицами и их свойства. Прямая на плоскости

Министерство образования и науки Российской Федерации

ФГБОУ ВПО

«Вятский Государственный Университет»

Реферат на тему :

«Матрицы. Операции над матрицами и их свойства. Прямая на плоскости»»

Выполнила студентка группы ИВТ-11

Долженкова Наталия Алексеевна

Зачетная книжка № Д10-ФАВТ-2012-26

§ 1. Матрицы.

Основные обозначения

1. Пусть дано некоторое числовое поле K.

Определение1. Прямоугольную таблицу чисел из поля K

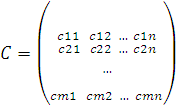(1)

будем называть матрицей. Если m=n, то матрица то матрица называется квадратной,       а число m, равное n, — ее порядком. В общем же случае матрица называется прямоугольной (с размерами m×n) или m×n-матрицей. Числа, составляющие матрицу, называются ее элементами.

Обозначения. При двухиндексном обозначении элементов первый индекс всегда указывает номер строки, а второй индекс — номер столбца, на пересечении которых стоит данный элемент.

Наряду с обозначениями матрицы (1) будем употреблять и сокращенное обозначение 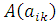 (i=1,2,…,m; k=1,2,…,n)

Часто матрицу (1) будем обозначать также одной буквой, например матрица A. Если A — квадратная матрица порядка n, то будем писать: 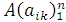 Определитель квадратной матрицы  будем обозначать так:   .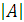

Квадратную матрицу, у которой все элементы, расположенные вне главной диагонали, равны нулю,

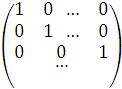
мы будем называть диагональной

  

Сложение и умножение прямоугольных матриц

Определим основные операции над матрицами:

·        сложение матриц,

·        умножение матрицы на число  

·        умножение матриц.

1. Определение 2. Суммой двух прямоугольных матриц 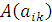  и 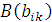  одинаковых размеров m×n называется матрица  C=( 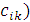тех же размеров, элементы которой равны суммам соответствующих элементов данной матрицы: 

C=A+B,  если  (i=1,2,…,m; k=1,2,…,n)

    Операция нахождения суммы данных матриц называется сложением матриц.

Согласно определению 2, складывать можно только прямоугольные матрицы одинаковых размеров.

Из определения сложения матриц непосредственно следует, что эта операция обладает переместительным и сочетательным свойствами:

1°   A+B=B+A

2°   (A+B)+C=A+(B+C)                             .

Здесь  A,B,C— произвольные прямоугольные матрицы одинаковых размеров.

Операция сложения матриц естественным образом распространяется на случай любого числа слагаемых.

2. Определение 3. Произведением матрицы 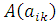 (i=1,2,…,m; k=1,2,…,n) на число α из K называется матрица  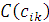 (i=1,2,…,m; k=1,2,…,n) элементы которой получаются из соответствующих элементов матрицы A умножением на число α:

C=αA

если

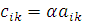  (i=1,2,…,m; k=1,2,…,n)

Операция нахождения произведения матрицы на число называется умножением матрицы на число.

Пример

+

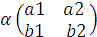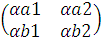
Легко видеть, что

1° α(A+B)= αA+ αB

2° ( α+β)A= αA+ βA

3° ( αβ)A=α(βA)

Здесь 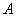,  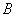— прямоугольные матрицы одинаковых размеров, 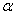,  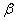— числа из поля .

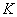Разность  A-B двух прямоугольных матриц одинаковых размеров определяется равенством

A-B=A+(-1)B

Если 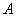 — квадратная матрица порядка n, а α — число из K, то

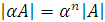
3. Определение 4. Произведением двух прямоугольных матриц

  

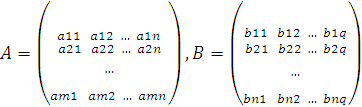
называется матрица,

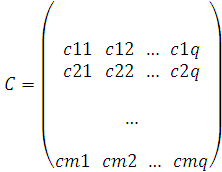
у которой элемент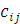, стоящий на пересечении i-й строки и j-го столбца, равен «произведению» i-й строки первой матрицы A на j-й столбец второй матрицы B

Операция нахождения произведения данных матриц называется умножением матриц.

Заметим, что операция умножения двух прямоугольных матриц выполнима лишь в том случае, когда число столбцов в первом сомножителе равно числу строк во втором. В частности, умножение всегда выполнимо, если оба сомножителя — квадратные матрицы одного и того же порядка. Обратим внимание читателя и на то, что даже в этом частном случае умножение матриц не обладает переместительным свойством.

    Если AB=BA, то матрицы A и B называются перестановочными или коммутирующими между собой.

<…>

Легко проверяется сочетательное свойство умножения матриц, а также распределительное свойство умножения относительно сложения:

1° (AB)C=A(BC)                                  

2°  (A+B)C=AC+BC                                                      (12)

3°   A(B+C)=AB+AC                     

Операция умножения матриц естественным образом распространяется на случай нескольких сомножителей.

§ 2. Прямая на плоскости

Определение1.Любая прямая на плоскости может быть задана уравнением первого порядка

Ах + Ву + С = 0,

причем постоянные А, В не равны нулю одновременно. Это уравнение первого порядка называют общим уравнением прямой. В зависимости от значений постоянных А,В и С возможны следующие частные случаи:

•  C = 0, А ≠0, В ≠ 0 – прямая проходит через начало координат

•  А = 0, В ≠0, С ≠0 { By + C = 0}- прямая параллельна оси Ох

•  В = 0, А ≠0, С ≠ 0 { Ax + C = 0} – прямая параллельна оси Оу

•  В = С = 0, А ≠0 – прямая совпадает с осью Оу

•  А = С = 0, В ≠0 – прямая совпадает с осью Ох

Уравнение прямой может быть представлено в различном виде в зависимости от каких – либо заданных начальных условий.

Уравнение прямой по точке и вектору нормали

Определение2. В декартовой прямоугольной системе координат вектор с компонентами (А, В) перпендикулярен прямой , заданной уравнением Ах + Ву + С = 0.

Уравнение прямой, проходящей через две точки

Пусть в пространстве заданы две точки M ₁ ( x ₁ , y ₁ , z ₁ ) и M₂ ( x ₂, y ₂ , z ₂ ), тогда уравнение прямой, проходящей через эти точки:

Если какой- либо из знаменателей равен нулю, следует приравнять нулю соответствующий числитель. На плоскости записанное выше уравнение прямой упрощается:

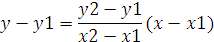
если х ₁ ≠ х₂ и х = х ₁ , если х ₁ = х₂ .

Дробь 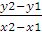= k называется угловым коэффициентомпрямой.

Уравнение прямой по точке и угловому коэффициенту

Если общее уравнение прямой Ах + Ву + С = 0 привести к виду:

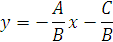
и обозначить , т.е 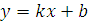 то полученное уравнение называется уравнением прямой с угловым коэффициентом k.

Уравнение прямой по точке и направляющему вектору

По аналогии с пунктом, рассматривающим уравнение прямой через вектор нормали можно ввести задание прямой через точку и направляющий вектор прямой.

Определение3. Каждый ненулевой вектор 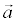( α₁ , α₂ ), компоненты которого удовлетворяют условию А α₁ + В α₂ = 0 называется направляющим вектором прямой

Ах + Ву + С = 0.

Уравнение прямой в отрезках

Если в общем уравнении прямой Ах + Ву + С = 0 С≠0, то, разделив на –С, получим: 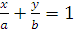 , где

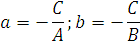
Геометрический смысл коэффициентов в том, что коэффициент а является координатой точки пересечения прямой с осью Ох, а b – координатой точки пересечения прямой с осью Оу.

Нормальное уравнение прямой

Если обе части уравнения Ах + Ву + С = 0 разделить на число 

  , которое называется нормирующем множителем, то получим

xcosφ + ysinφ - p = 0 –

нормальное уравнение прямой. Знак ± нормирующего множителя надо выбирать так, чтобы μ * С < 0. р – длина перпендикуляра, опущенного из начала координат на прямую, а φ - угол, образованный этим перпендикуляром с положительным направлением оси Ох.

Cледует отметить, что не каждую прямую можно представить уравнением в отрезках, например, прямые, параллельные осям или проходящие через начало координат.

Угол между прямыми на плоскости

Определение4.Если заданы две прямые y = k₁ x + b₁ , y = k ₂x + b₂ , то острый угол между этими прямыми будет определяться как

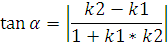
Две прямые параллельны, если k₁ = k₂ . Две прямые перпендикулярны, если k₁ = -1/ k₂ .

Теорема. Прямые Ах + Ву + С = 0 и А ₁ х + В₁ у + С₁ = 0 параллельны, когда пропорциональны коэффициенты А₁ = λА, В₁ = λВ. Если еще и С₁ = λС, то прямые совпадают. Координаты точки пересечения двух прямых находятся как решение системы уравнений этих прямых.

Уравнение прямой, проходящей через данную точку

перпендикулярно данной прямой

Определение. Прямая, проходящая через точку М₁ (х₁ , у₁ ) и перпендикулярная к прямой у = kx + b представляется уравнением:

Расстояние от точки до прямой

Теорема. Если задана точка М(х₀ , у₀ ), то расстояние до прямой Ах + Ву + С =0 определяется как

 d=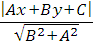

Доказательство. Пусть точка М ₁(х ₁, у ₁) – основание перпендикуляра, опущенного из точки М на заданную прямую. Тогда расстояние между точками М и М₁ :

 

Координаты x₁ и у₁ могут быть найдены как решение системы уравнений:

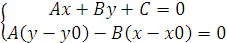
Второе уравнение системы – это уравнение прямой, проходящей через заданную точку М ₀ перпендикулярно заданной прямой. Если преобразовать первое уравнение системы к виду:

A(x – x ₀ ) + B(y – y₀ ) + Ax₀ + By₀ + C = 0,

то, решая, получим:

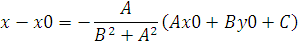
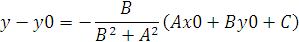
Подставляя эти выражения в уравнение (1), находим:

 d=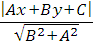

Теорема доказана.

Список используемой литературы:

1)    А.Г Курош – «Курс высшей алгебры» (издание девятое)

2)    П. Ланкастер – «Теория матриц»

3)    .Никулина Л.С., Степанова А.А. «Высшая математика»  (Учеб. пособие)