МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
федеральное государственное бюджетное образовательное учреждение
высшего профессионального образования
«Забайкальский государственный университет»
РЕФЕРАТ
Тема: Геометрические и физические приложения определенного интеграла
Выполнил:
студент 2 курса
группы ИФ-14 ФЕНМит
Бояркин Сергей
Проверил:
Беломестнова Вера Ревокатовна
Чита 2016
Геометрические приложения определенного интеграла
· Схемы применения определенного интеграла
Пусть
требуется найти значение какой – либо геометрической или физической величины 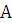 (площадь
фигуры, объем тела, давление жидкости на вертикальную пластину и т.д.),
связанной с отрезком
(площадь
фигуры, объем тела, давление жидкости на вертикальную пластину и т.д.),
связанной с отрезком 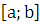 изменения
независимой переменной x.
Предполагается, что при разбиении отрезка
изменения
независимой переменной x.
Предполагается, что при разбиении отрезка 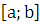 точкой
точкой
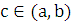 на
части [a,c]
и [c,b]
значение величины
на
части [a,c]
и [c,b]
значение величины 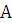 ,
соответствующее всему отрезку
,
соответствующее всему отрезку 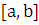 равно
сумме ее значений, соответствующих [a,c]
и [c b]
равно
сумме ее значений, соответствующих [a,c]
и [c b]
Для
нахождения этой величины 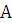 можно
руководствоваться одной из двух схем: I
схема (или метод интегральных сумм) и II
схема (или метод дифференциала).
можно
руководствоваться одной из двух схем: I
схема (или метод интегральных сумм) и II
схема (или метод дифференциала).
Первая схема базируется на определении определенного интеграла.
1.
Точками 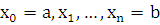 разбить
отрезок
разбить
отрезок 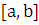 на
на
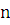 частей.
В соответствии с этим, интересующая нас величина
частей.
В соответствии с этим, интересующая нас величина 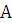 разобьется
на
разобьется
на 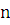 «элементарных
слагаемых»
«элементарных
слагаемых» 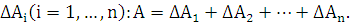
2. Представить каждое «элементарное слагаемое» в виде произведения некоторой функции (определяемой из условия задачи), вычисленной в произвольной точке соответствующего отрезка на его длину:
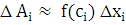 .
.
При
нахождении приближенного значения 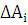 допустимы
некоторые упрощения: дугу на малом участке можно заменить хордой, стягивающей
ее концы; переменную скорость на малом участке можно приближенно считать
постоянной и т. д.
допустимы
некоторые упрощения: дугу на малом участке можно заменить хордой, стягивающей
ее концы; переменную скорость на малом участке можно приближенно считать
постоянной и т. д.
Получим
приближенное значение величины 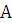 в
виде интегральной суммы:
в
виде интегральной суммы:
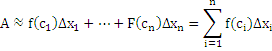
3.
Искомая величина 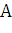 равна пределу интегральной суммы, т. е.
равна пределу интегральной суммы, т. е.
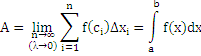
Указанный «метод сумм» основан на представлении интеграла как сумма бесконечно большого числа бесконечно малых слагаемых.
Схема I была применена для выяснения геометрического и физического смысла определенного интеграла.
Вторая схема представляет собой несколько видоизмененную схему I и называется «метод дифференциала» или «метод отбрасывания бесконечно малых высших порядков»:
1)
на отрезке 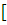 а,b
а,b выбираем
произвольное значение х и рассматриваем переменный отрезок [a,x
выбираем
произвольное значение х и рассматриваем переменный отрезок [a,x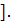 На
этом отрезке величина
На
этом отрезке величина 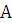 становится
функцией
становится
функцией 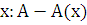 ,
т.
е. считаем, что часть искомой величины
,
т.
е. считаем, что часть искомой величины 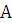 есть
неизвестная функция
есть
неизвестная функция 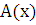 ,
где
,
где
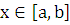 -
один из параметров величины
-
один из параметров величины 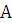 ;
;
2)
находим главную часть приращения 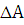 при
изменении x
на
малую величину
при
изменении x
на
малую величину  ,
т.
е. находим дифференциал d
,
т.
е. находим дифференциал d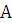 функции
функции
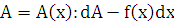 ,
где
,
где
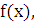 определяемая
из условия задачи, функция переменной x
(здесь также возможны различные упрощения);
определяемая
из условия задачи, функция переменной x
(здесь также возможны различные упрощения);
3)
считая, что 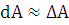 при
при
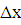
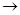
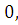 находим
искомую величину путем интегрирования
находим
искомую величину путем интегрирования 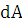 в
пределах от
в
пределах от  до
до
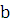 :
:
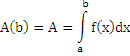
· Вычисление длины дуги плоской кривой
Пусть
в прямоугольных координатах дана плоская кривая AB,
уравнение которой, 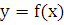 ,
где
,
где 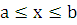 .
.
Под длиной дуги AB понимается предел, к которому стремиться длина ломаной линии, вписанной в эту дугу, когда число звеньев ломаной неограниченно возрастает, а длина наибольшего звена ее стремиться к нулю.
Покажем,
что если функция 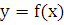 и
ее производная
и
ее производная 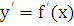 непрерывна
на отрезке
непрерывна
на отрезке 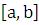 ,
то кривая АВ имеет длину, равную
,
то кривая АВ имеет длину, равную

Применим схему I (метод сумм).
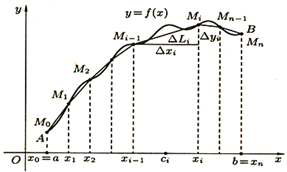
1.
Точками 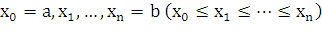 разобьем отрезок
разобьем отрезок  на
на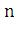 частей (рис. 2). Пусть этим точкам
соответствуют точки
частей (рис. 2). Пусть этим точкам
соответствуют точки 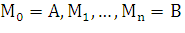 на кривой AB. Проведем хорды
на кривой AB. Проведем хорды 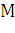
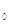

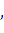
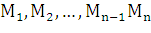 , длины которых обозначим
соответственно через
, длины которых обозначим
соответственно через 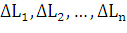
|
Получим
ломанную  длина
которой равна
длина
которой равна
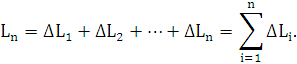
2.
Длину хорды (или
звена ломаной)  можно найти по теореме Пифагора из
треугольника с катетами Δ
можно найти по теореме Пифагора из
треугольника с катетами Δ и Δ
и Δ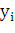 :
:
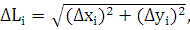 где
где
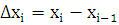 ,
,
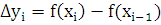 .
.
По теореме Лагранжа о конечном приращении функции
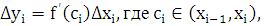 поэтому
поэтому
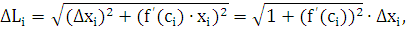
а
длина всей ломанной 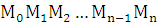 равна
равна
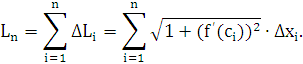
3.
Длина 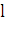 кривой AB, по определению, равна
кривой AB, по определению, равна
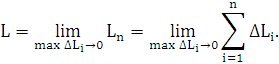
Заметим,
что при  также
и
также
и 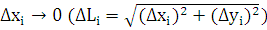 и,
следовательно,
и,
следовательно, 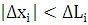 .
Функция
.
Функция 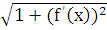 непрерывна
на отрезке
непрерывна
на отрезке 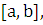 так
как, по условию, непрерывна функция
так
как, по условию, непрерывна функция 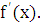 Следовательно,
существует предел интегральной суммы (1), когда
Следовательно,
существует предел интегральной суммы (1), когда 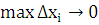 :
:
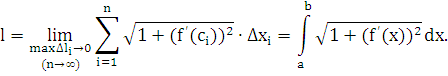
Таким образом,

Если уравнение кривой АВ задано в параметрической форме
 ,
,
Где
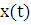 и
и
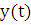 –
непрерывные функции с непрерывными производными и
–
непрерывные функции с непрерывными производными и 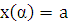 ,
,
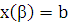 ,
то длина
,
то длина 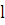 кривой
АВ находится по формуле
кривой
АВ находится по формуле

Формула (3) может быть получена из формулы (2) подстановкой
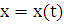 ,
,
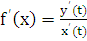
· Вычисление объема тела
Вычисление объема тела по известным площадям параллельных сечений.
Пусть
требуется найти объем 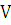 тела,
причем известны площади
тела,
причем известны площади 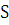 сечений
этого тела плоскостями, перпендикулярными некоторой оси, например оси
сечений
этого тела плоскостями, перпендикулярными некоторой оси, например оси 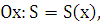
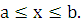
Применим схему II (метод дифференциала).
1.
Через
произвольную точку 
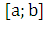 проведем плоскость, перпендикулярную оси
проведем плоскость, перпендикулярную оси 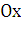 (рис. 3). Обозначим через
(рис. 3). Обозначим через 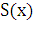 площадь сечения тела этой плоскостью;
площадь сечения тела этой плоскостью; 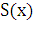 считаем известной и непрерывно изменяющейся при изменении
считаем известной и непрерывно изменяющейся при изменении 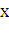 . Через
. Через  обозначим объем части тела, лежащее
левее плоскости. Будем считать, что на отрезке
обозначим объем части тела, лежащее
левее плоскости. Будем считать, что на отрезке 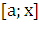 величина
величина 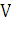 есть функция от x, т. е.
есть функция от x, т. е.

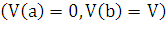
2.
Находим
дифференциал 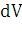 функции
функции 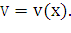 Он представляет собой «элементарный
слой» тела, заключенный между параллельными плоскостями, пересекающими ось
Он представляет собой «элементарный
слой» тела, заключенный между параллельными плоскостями, пересекающими ось 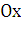 в точках
в точках 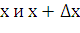 , который приближенно может быть
принят за цилиндр с основанием
, который приближенно может быть
принят за цилиндр с основанием 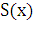 и высотой
и высотой 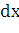 . Поэтому дифференциал объема
. Поэтому дифференциал объема 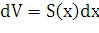 .
.
3.
Находим искомую
величину 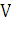 путем интегрирования
путем интегрирования 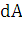 в пределах от
в пределах от 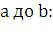

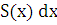 .
.
Полученная формула называется формулой
объема тела 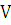 по
площади параллельных сечений.
по
площади параллельных сечений.
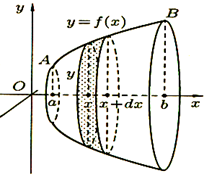
Объем тела вращения.
Пусть
вокруг оси 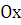 вращается
криволинейная трапеция, ограниченная непрерывной линией
вращается
криволинейная трапеция, ограниченная непрерывной линией 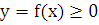 ,
отрезком
,
отрезком 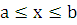 и
прямыми
и
прямыми 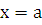 и
и
 (рис.
4).
Полученная от вращения фигура называется телом вращения.
(рис.
4).
Полученная от вращения фигура называется телом вращения.
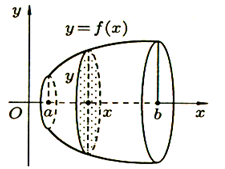
Сечение
этого тела плоскостью, перпендикулярной оси 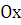 ,
проведенной
через произвольную точку
,
проведенной
через произвольную точку 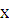 оси
оси
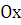
 ,
есть круг с радиусом
,
есть круг с радиусом 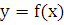 .
Следовательно,
.
Следовательно,

Применяя формулу (4) объема тела по площади параллельных сечений, получаем
|
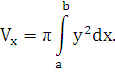
Если
криволинейная трапеция ограничена графиком непрерывной функции 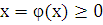 и
прямыми
и
прямыми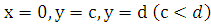 ,
то объем тела, образованного вращением этой трапеции вокруг оси
,
то объем тела, образованного вращением этой трапеции вокруг оси 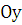 ,
по аналогии с формулой (5), равен
,
по аналогии с формулой (5), равен
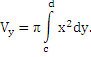
· Вычисление площади поверхности вращения
Пусть
кривая АВ является графиком функции 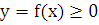 ,
где
,
где 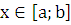 ,
а
функция
,
а
функция 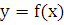 и
ее производная
и
ее производная 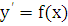 непрерывны
на этом отрезке.
непрерывны
на этом отрезке.
Найдем
площадь 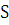 поверхности,
образованной вращением кривой АВ вокруг оси
поверхности,
образованной вращением кривой АВ вокруг оси 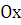 .
.
Применим схему II (метод дифференциала).
1.
Через
произвольную точку 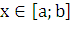 проведем плоскость, перпендикулярную
оси
проведем плоскость, перпендикулярную
оси 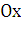 . Плоскость пересекает поверхность вращения по окружности с
радиусом
. Плоскость пересекает поверхность вращения по окружности с
радиусом  (рис. 5). Величина
(рис. 5). Величина 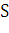 поверхности части фигуры вращения,
лежащей левее плоскости, является функцией от
поверхности части фигуры вращения,
лежащей левее плоскости, является функцией от 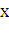 , т.е.
, т.е.
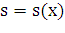
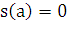 и
и 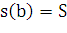
2.
Дадим аргументу 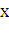 приращение
приращение 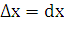 . Через точку
. Через точку 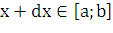 также проведем плоскость, перпендикулярную оси
также проведем плоскость, перпендикулярную оси 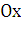 . Функция
. Функция  получит приращение
получит приращение 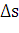 . Найдем дифференциал площади
. Найдем дифференциал площади 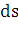 , заменяя образованную между сечениями фигуру усеченным
конусом, образующая которого равна
, заменяя образованную между сечениями фигуру усеченным
конусом, образующая которого равна  , а радиусы оснований равны
, а радиусы оснований равны 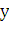 и
и 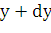 . Площадь его боковой поверхности равна
. Площадь его боковой поверхности равна
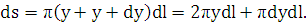
Отбрасывая
произведение 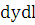 как
бесконечно малую высшего порядка, чем
как
бесконечно малую высшего порядка, чем 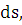 получаем
получаем
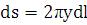 ,
или, так как
,
или, так как
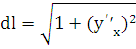 ,
то
,
то 
3.
Интегрируя
полученное равенство в пределах 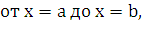 получаем
получаем
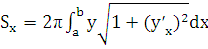 .
.
Если кривая AB
задана параметрическими уравнениями 


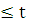

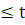

 то
формула для площади поверхности вращения принимает вид
то
формула для площади поверхности вращения принимает вид
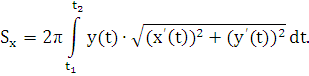
· Вычисление площади плоской фигуры
Пусть
функция 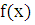 непрерывна
на сегменте
непрерывна
на сегменте 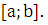 Если
Если
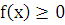 на
[a,b],
то площадь S криволинейной
трапеции, ограниченной линиями y=f(x),
y=0, x=a,
x=b,
равна интегралу
на
[a,b],
то площадь S криволинейной
трапеции, ограниченной линиями y=f(x),
y=0, x=a,
x=b,
равна интегралу
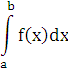
Если
же 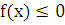 на
на
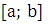 то
—
то
— 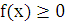 на
на
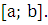 Поэтому
площадь S соответствующей
криволинейной трапеции выразится формулой
Поэтому
площадь S соответствующей
криволинейной трапеции выразится формулой

Если,
наконец, кривая 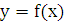 пересекает
ось Ох, то сегмент
пересекает
ось Ох, то сегмент 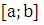 надо
разбить на части, в пределах которых
надо
разбить на части, в пределах которых  не
меняет
знака, и к каждой такой части применить ту из формул, которая ей соответствует.
не
меняет
знака, и к каждой такой части применить ту из формул, которая ей соответствует.
· Вычисление площади цилиндрической поверхности
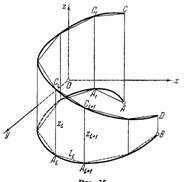
Введем
дугу 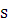 в
качестве параметра; тогда не только уравнения
в
качестве параметра; тогда не только уравнения 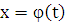 и
и
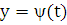 кривой
AB заменятся уравнениями
кривой
AB заменятся уравнениями 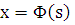 и
и
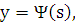 но
и уравнение
но
и уравнение 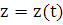 перейдет
в уравнение
перейдет
в уравнение 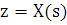 .
Впишем в кривую АВ ломаную
.
Впишем в кривую АВ ломаную  и,
в соответствии с этим, в кривую CD
– ломаную
и,
в соответствии с этим, в кривую CD
– ломаную  ,
из трапеций
,
из трапеций 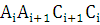 составим
призматическую поверхность, вписанную в рассматриваемую цилиндрическую
поверхность. Под площадью цилиндрической поверхности будем понимать предел P
площади Q призматической
поверхности при стремлении к нулю наибольшей из частичных дуг. Полагая, что
составим
призматическую поверхность, вписанную в рассматриваемую цилиндрическую
поверхность. Под площадью цилиндрической поверхности будем понимать предел P
площади Q призматической
поверхности при стремлении к нулю наибольшей из частичных дуг. Полагая, что 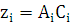 ,
имеем
,
имеем
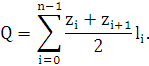
Предел суммы будет вычисляться по формуле
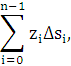
в которой легко узнать интегральную сумму. Окончательно

Возвращаясь к произвольному параметру t, легко получить и общую формулу
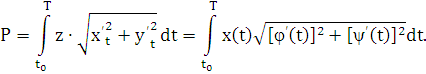
Наконец,
для случая явного задания кривой АВ: y=f(x)
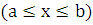 эта
формула перепишется так:
эта
формула перепишется так:
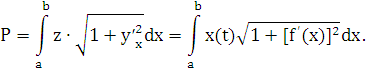
определенный интеграл геометрический физический
Физические приложения определенного интеграла
С помощью физических приложений вычисляются: работа переменной силы, давление жидкости на вертикальную пластинку, статические моменты и координаты центра тяжести плоской кривой и плоской фигуры.1. Работа переменной силы
Пусть под
действием некоторой силы 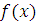 материальная точка М движется по прямой в направлении оси
материальная точка М движется по прямой в направлении оси 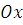 . Требуется найти работу, произведённую силой
. Требуется найти работу, произведённую силой 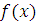 при перемещении точки М из положения
при перемещении точки М из положения 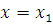 в положение
в положение 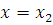 .
.
1) Если
сила постоянна  , то работа выражается следующим образом
, то работа выражается следующим образом  .
.
2) Если сила переменная величина, то
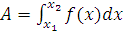 .
.
Пример.
Два
электрических заряда 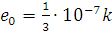 и
и 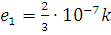 находятся на оси
находятся на оси 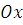 соответственно в точках
соответственно в точках 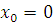 и
и 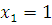 . Какая работа будет произведена, если второй заряд переместится в
точку
. Какая работа будет произведена, если второй заряд переместится в
точку  ? (Сила взаимодействия зарядов
? (Сила взаимодействия зарядов 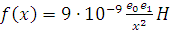 ).
).
Решение:
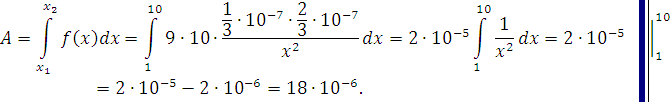
2. Давление жидкости на вертикальную пластинку
По закону Паскаля давление жидкости
на горизонтальную пластину равно весу столба этой жидкости, имеющего основанием
пластинку, а высотой — глубину ее погружения от свободной поверхности жидкости,
т.е. 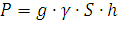 , где
, где 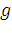 — ускорение свободного падения,
— ускорение свободного падения, 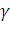 — плотность жидкости,
— плотность жидкости,  – площадь пластинки,
– площадь пластинки,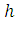 – глубина ее погружения.
– глубина ее погружения.
По этой формуле нельзя искать
давление жидкости на вертикально погруженную пластинку, так как ее разные точки
лежат на разных глубинах. Пусть в жидкость погружена вертикально пластина,
ограниченная линиями 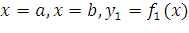 и
и 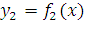 ; система координат выбрана так, как
указано на рисунке 11. Для нахождения давления
; система координат выбрана так, как
указано на рисунке 11. Для нахождения давления 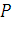 жидкости на эту пластину применим
схему II (метод дифференциала).
жидкости на эту пластину применим
схему II (метод дифференциала).
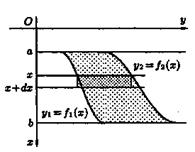
Рисунок 11
1. Пусть часть искомой величины  есть функция от
есть функция от  :
: , т.е.
, т.е. 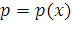 — давление на часть пластины,
соответствующее отрезку
— давление на часть пластины,
соответствующее отрезку 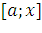 значений переменной
значений переменной 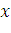 , где
, где 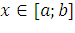
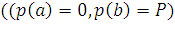 .
.
2. Дадим аргументу 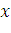 приращение
приращение 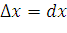 . Функция
. Функция 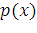 получит приращение
получит приращение  (на рисунке — полоска-слой толщины
(на рисунке — полоска-слой толщины 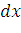 ). Найдем дифференциал
). Найдем дифференциал 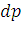 этой функции. Ввиду малости
этой функции. Ввиду малости 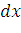 будем приближенно считать полоску
прямоугольником, все точки которого находятся на одной глубине
будем приближенно считать полоску
прямоугольником, все точки которого находятся на одной глубине 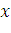 , т.е. пластинка эта —
горизонтальная. Тогда по закону Паскаля
, т.е. пластинка эта —
горизонтальная. Тогда по закону Паскаля 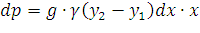 , где
, где 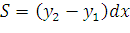 ,
,
 .
.
3. Интегрируя полученное равенство в
пределах от  до
до 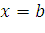 , получим:
, получим:

3. Вычисление статических моментов и координат центра тяжести плоской кривой
Пусть на плоскости 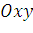 задана система материальных точек
задана система материальных точек 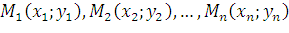 соответственно с массами
соответственно с массами  .
.
Статическим моментом 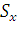 системы материальных точек
относительно оси
системы материальных точек
относительно оси 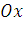 называется сумма произведений масс
этих точек на их ординаты (т.е. на расстояния этих точек от оси
называется сумма произведений масс
этих точек на их ординаты (т.е. на расстояния этих точек от оси 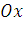 ):
):
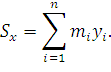
Аналогично определяется статический
момент 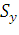 этой системы относительно оси
этой системы относительно оси 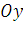 :
:

Если массы распределены непрерывным образом вдоль некоторой кривой, то для выражения статического момента понадобится интегрирование.
Пусть 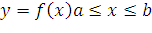 — это уравнение материальной кривой
— это уравнение материальной кривой 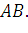 Будем считать ее однородной с
постоянной линейной плотностью
Будем считать ее однородной с
постоянной линейной плотностью 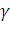
 . Для произвольного
. Для произвольного 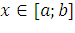 на кривой
на кривой 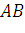 найдется точка с координатами
найдется точка с координатами 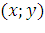 . Выделим на кривой элементарный
участок длины
. Выделим на кривой элементарный
участок длины 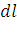 , содержащий точку
, содержащий точку 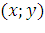 . Тогда масса этого участка равна
. Тогда масса этого участка равна 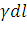 . Примем этот участок
. Примем этот участок 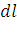 приближенно за точку, отстоящую от
оси
приближенно за точку, отстоящую от
оси 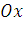 на расстоянии
на расстоянии 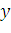 . Тогда дифференциал статического
момента
. Тогда дифференциал статического
момента 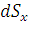 ("элементарный момент")
будет равен
("элементарный момент")
будет равен 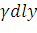 , т.е.
, т.е. 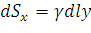 (рисунок 12).
(рисунок 12).
Отсюда
следует, что статический момент 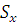 кривой
кривой 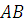 относительно оси
относительно оси 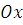 равен:
равен:
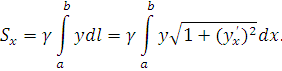
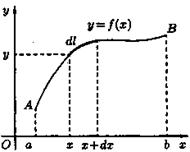
Рисунок 12
Аналогично
находим  :
:
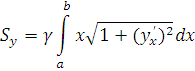
Статические моменты 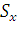 и
и 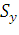 кривой позволяют легко установить
положение ее центра тяжести (центра масс).
кривой позволяют легко установить
положение ее центра тяжести (центра масс).
Центром тяжести материальной плоской
кривой 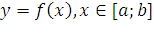 называется точка плоскости,
обладающая следующим свойством: если в этой точке сосредоточить всю массу
называется точка плоскости,
обладающая следующим свойством: если в этой точке сосредоточить всю массу 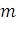 заданной кривой, то статический
момент этой точки относительно любой координатной оси будет равен статическому
моменту всей кривой
заданной кривой, то статический
момент этой точки относительно любой координатной оси будет равен статическому
моменту всей кривой 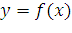 относительно той же оси. Обозначим
через
относительно той же оси. Обозначим
через 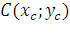 центр тяжести кривой
центр тяжести кривой  . Из определения центра тяжести
следуют равенства
. Из определения центра тяжести
следуют равенства 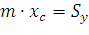 и
и 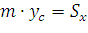 или
или 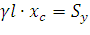 и
и 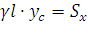 .
.
Отсюда 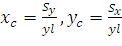 или
или 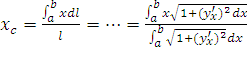 ;
;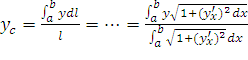 .
.
Пример. Найти центр тяжести однородной дуги окружности
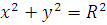 , расположенной в первой координатной четверти
(рисунок 13).
, расположенной в первой координатной четверти
(рисунок 13).
Решение: Очевидно, длина указанной дуги окружности равна 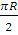 , т.е.
, т.е. 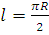 .
.
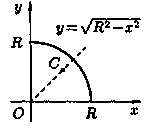
Рисунок 13
Найдем
статический момент ее относительно оси 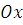 . Так как уравнение дуги есть
. Так как уравнение дуги есть  и
и
 , то
, то 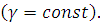
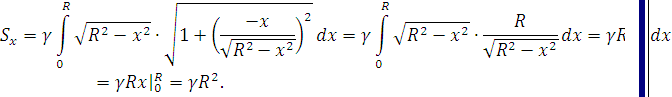
Стало быть,
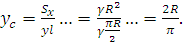
Так как
данная дуга симметрична относительно биссектрисы первого координатного угла, то
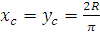 . Итак, центр тяжести имеет координаты
. Итак, центр тяжести имеет координаты
 .
.
4. Вычисление статических моментов и координат центра тяжести плоской фигуры
Пусть дана материальная плоская фигура (пластинка), ограниченная кривой  и прямыми
и прямыми 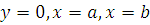 (рисунок 14).
(рисунок 14).
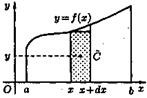
Рисунок 14
Будем
считать, что поверхностная плотность пластинки постоянна 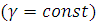 . Тогда масса всей пластинки равна
. Тогда масса всей пластинки равна  , т.е.
, т.е.
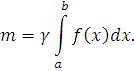
Выделим
элементарный участок пластинки в виде бесконечно узкой вертикальной полосы и
будем приближенно считать его прямоугольником. Тогда масса его равна 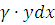 . Центр тяжести
. Центр тяжести  прямоугольника лежит на пересечении диагоналей прямоугольника.
Эта точка
прямоугольника лежит на пересечении диагоналей прямоугольника.
Эта точка  отстоит от оси
отстоит от оси 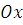 на
на 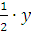 , а от оси
, а от оси 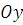 на
на 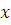 (приближенно; точнее на расстоянии
(приближенно; точнее на расстоянии 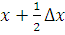 ). Тогда для элементарных статических моментов относительно осей
). Тогда для элементарных статических моментов относительно осей 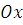 и
и 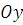 выполнены соотношения
выполнены соотношения
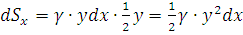 и
и 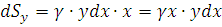
Следовательно,
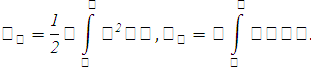
По аналогии с плоской кривой
получаем, обозначив координаты центра тяжести плоской фигуры (пластинки) через 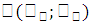 , что
, что 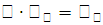 ,
, 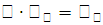 . Отсюда
. Отсюда
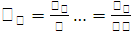 и
и 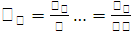 или
или 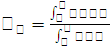 ,
,
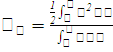 .
.
Пример. Найдем координаты центра тяжести полукруга
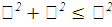 ,
, 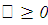
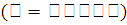 (рисунок 15).
(рисунок 15).
Решение: Очевидно (ввиду симметрии фигуры относительно оси 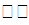 ), что
), что 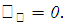 Площадь полукруга равна
Площадь полукруга равна 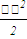 .
Находим
.
Находим 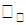 :
:

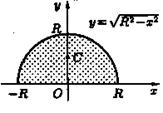
Рисунок 15
Стало быть,
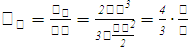 .
Итак, центр тяжести имеет координаты
.
Итак, центр тяжести имеет координаты 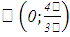 .
.
Заключение
Рассмотренные выше примеры практических задач, дают нам ясное представление значимости определенного интеграла для их разрешимости.
Трудно назвать научную область, в которой бы не применялись методы интегрального исчисления, в общем, и свойства определенного интеграла, в частности. Так в процессе выполнения реферата мною были рассмотрены примеры практических задач в области физики, геометрии, механики. Конечно, это еще далеко не исчерпывающий список наук, которые используют интегральный метод для поиска устанавливаемой величины при решении конкретной задачи, и установлении теоретических фактов.
Также определенный интеграл используется для изучения собственно самой математики. Например, при решении дифференциальных уравнений, которые в свою очередь вносят свой незаменимый вклад в решение задач практического содержания. Можно сказать, что определенный интеграл – это некоторый фундамент для изучения математики. Отсюда и важность знания методов их решения.
Из всего выше сказанного понятно, почему знакомство с определенным интегралом происходит еще в рамках средней общеобразовательной школы, где ученики изучают не только понятие интеграла и его свойства, но и некоторые его приложения.
Список использованных источников
1. Дифференциальное и интегральное исчисления для вузов, Том 2 / Н.С. Пискунов – М.: Наука, 1985. -560с.
2. Конспект лекций по высшей математике / Д.Т. Письменный – M.: Айрис – пресс, 2003. – 288 c.
3. Математический анализ для школьников / Л.Н. Понтрягин – 2-е изд., перераб. - М.: Наука, 1983г.
4. Высшая математика – М.: Просвещение, 1993. – 319. Баврин И.И.
5. Высшая математика - М: Наука, 2003 – 684c. Шипачёв В.С.














 (zip - application/zip)
(zip - application/zip)