ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
Томский политехнический университет
Кафедра теоретической и прикладной механики
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
К КУРСОВОМУ ПРОЕКТУ ПО ТЕОРИИ МЕХАНИЗМОВ И МАШИН
Структурный, кинематический анализ и силовой расчет
рычажного механизма. Синтез зубчатого и кулачкового механизмов.
Выполнил студент группы З-8Л31/21
Толстобров Антон Анатольевич
Руководил доцент:
Горбенко Михаил Владимирович
Томск 2016
Томский политехнический университет
Кафедра теоретической и прикладной механики
КУРСОВОЙ ПРОЕКТ ПО ТЕОРИИ МЕХАНИЗМОВ И МАШИН
Студенту 150700 «Машиностроение» факультета, гр. З-8Л31/21
Толстоброву Антону Анатольевичу
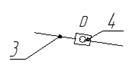
РЫЧАЖНЫЙ МЕХАНИЗМ
Кинематический анализ и силовой расчет механизма
Задание №606
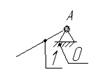
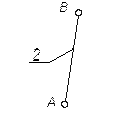
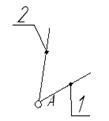
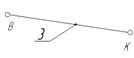
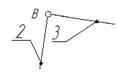
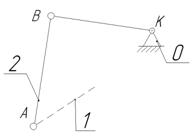
Схема механизма График силы (момента)
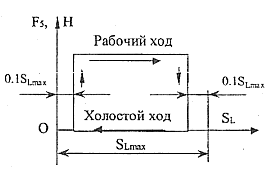
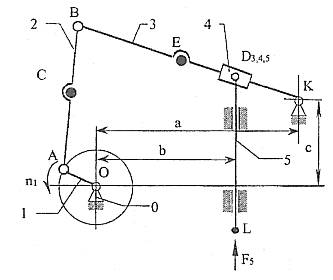
полезного сопротивления
Исходные данные:
Размеры звеньев: 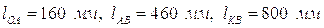
Частота вращения кривошипа n =70 об/мин;
Сила полезного сопротивления F5 =4800 Н;
Дополнительные условия: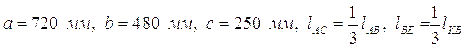 .
.
Дата выдачи задания: 10.06.2016
Срок выполнения: 5 месяцев
Руководитель: Горбенко Михаил Владимирович
Введение
Целью курсовой работы является ознакомление с анализом и синтезом основных механизмов входящих в большинство приводов машин.
Знакомство с анализом механизмов на примере анализа рычажного механизма, представляющего собой механизм преобразование вращения входного звена с постоянной скоростью в движение выходного звена со сложным законом изменения движения, в котором движение передаётся через низшие одноподвижные кинематические пары.
Знакомство с синтезом механизмов осуществляется на примере синтеза двух передач.
На примере синтеза зубчатых передач мы знакомимся с синтезом передач передающие движения нормальными силами зацепления через высшие двух подвижные кинематические пары, образуемые зацепляющимися зубьями. Также знакомимся с механизмами для подбора некоторых параметров, которые, например чисел зубьев колёс планетарных передач необходимо одновременно учитывать большое количество условий.
На примере синтеза кулачковой передачи мы знакомимся с синтезом передачи, воспроизводящейся сложным законом движения выходного звена, в котором движение передаётся через высшие двухподвижные кинематические пары трения, между кулачком и толкателем.
1. Рычажный механизм
1.1. Структурный анализ механизма
Цель структурного анализа – выявить строение (структуру) механизма:
- определить число звеньев механизма и назвать каждое из них;
- определить числа кинематических пар и дать их характеристику (соединения каких звеньев, вращательная, поступательная, низшая или высшая, какого класса);
- выявить структурные группы (группы Ассура), входящие в состав механизма, назвать их, определить класс группы, написать формулу строения;
- определить степень подвижности механизма;
- привести формулу строения для всего механизма.
Для наглядности выполним структурный анализ в форме таблицы.
Структурный анализ механизма Структурный анализ проведём по методике изложенной в [1, с. 6] Таблица 1 |
|||||||
|
Подвижные звенья. |
Кинематические пары. |
||||||
|
Схема |
Название |
Схема |
Вид |
Степень подвижности |
Символ. |
Класс пары |
Высшая или низшая |
|
|
Кривошип |
|
Вращат. |
1 |
В0.1 |
P5 |
Низшая |
|
|
Шатун |
|
Вращат. |
1 |
В1.2 |
P5 |
Низшая |
|
|
Коромысло (Кулиса) |
|
Вращат. |
1 |
В2.3 |
P5 |
Низшая |
|
|
Камень кулисы |
|
Вращат. |
1 |
В0.3 |
P5 |
Низшая |
|
|
Ползун |
|
Поступат. |
1 |
П3.4 |
P5 |
Низшая |
|
Число подвижных звеньев n = 5 |
|
Вращат. |
1 |
В4.5 |
P5 |
Низшая |
|
|
|
Поступат. |
1 |
П0.5 |
P5 |
Низшая |
||
|
Число кинематических пар: Всего - 7 Из них пятого класса P5=7 Четвертого P4=0 |
|||||||
|
Степень подвижности механизма: W=3n-2P5–P4=3·5-2·7-0=1 |
|||||||
|
Структурный состав механизма Структурный анализ проведём по методике изложенной в [1, с. 7] Таблица 2 |
|||||
Схема |
Название, класс, порядок, вид |
Число звеньев |
Число К.П. |
Формула Строения. |
|
|
Всего |
Поводковых |
||||
|
|
Начальный вращательный механизм. I класс |
1 |
1 |
----- |
В0.1 |
|
|
Двухзвенная двухповодковая группа. II класс II порядок I вид. |
2 |
3 |
2 |
[В1.2 -В2.3-В0.3] |
|
|
Двухзвенная двухповодковая группа. II класс II порядок IV вид. |
2 |
3 |
2 |
[П3.4 -В4.5-П0.5] |
|
Начальных механизмов: 1 Структурных групп (Групп Ассура): 2 Соединение групп: последовательное Класс механизма: II Порядок механизма: II Формула строения: В0.1-[В1.2 -В2.3-В0.3]-[П3.4 -В4.5-П0.5] |
|||||
1.2. Кинематический анализ механизма
В данном разделе необходимо:
1.2.1. Найти крайние положения механизма и построить траектории движения всех характерных точек механизма по 8-12 положениям механизма.
1.2.2. Кинематический анализ методом планов. Построить планы скоростей и ускорений для одного заданного положения механизма и определить:
1.2.3. линейные скорости всех характерных точек механизма;
1.2.4. угловые скорости всех звеньев механизма;
1.2.5. линейные ускорения всех характерных точек механизма;
1.2.6. угловые ускорения всех звеньев механизма;
1.2.7.определить и указать на схеме направления угловых скоростей и ускорений соответствующих звеньев (круговыми стрелками с обозначением номеров звеньев: w1 , w2 …и e1 , e2…).
В данной работе кинематический анализ выполняется методом планов, хотя существуют и другие методы (аналитический метод и метод графиков).
1.2.3. Определение линейных скоростей всех характерных точек
механизма
Анализ проведём по методике изложенной в [1, с. 3-15.]
План скоростей для положения 3
Определим скорость ведущей точки механизма, т.е. точки звена, закон движения которого задан. В нашем случае это точка А звена 1:
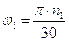 ,
,
где
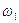 - угловая скорость
кривошипа,
- угловая скорость
кривошипа, 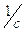 ;
;
n1 – частота
вращения звена 1, 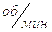 .
.

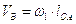 ,
,
где
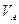 - скорость ведущей
точки механизма,
- скорость ведущей
точки механизма, 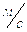 ;
;
lОА – длина кривошипа ОА, м.
Тогда:
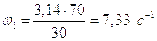 ;
;
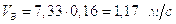 .
.
Примем масштаб построения плана скоростей:
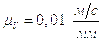 .
.
На плане скоростей:
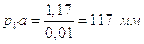 .
.
Выберем
произвольную точку-полюс плана скоростей 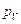 . Вектор
. Вектор 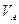 проведён перпендикулярно
кривошипу и направлен в сторону вращения звена 1(pVa).
проведён перпендикулярно
кривошипу и направлен в сторону вращения звена 1(pVa).
Скорость точки B может быть определена из совместного решения 2-х уравнений:
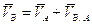 - для звена 2.
- для звена 2.
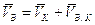 - для звена 3.
- для звена 3.
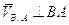 ,
, 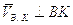 ,
,
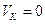 (неподвижная точка),
следовательно
(неподвижная точка),
следовательно 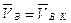 .
.
Строим план.
Построив план, получим:
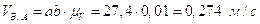 .
.
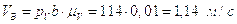 .
.
Найдем скорость точки С.
Скорость этой точки определим на основании свойства пропорциональности отрезков ac, аb на плане скоростей и размеров звеньев lAC, lАВ.
Получим следующее отношение:
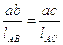 .
.
Отсюда находим:
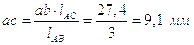 .
.
Построив план, получим:
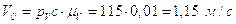 .
.
Найдем скорости точек D3, E.
Скорости этих точек определим на основании свойства пропорциональности отрезков be, bd3, bk на плане скоростей и размеров звеньев lBE, lBD, lBK.
Получим следующее отношение:
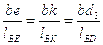 .
.
Отсюда находим:
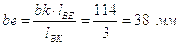 ;
;
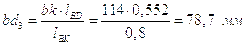 .
.
Построив план получим:
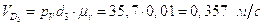 ;
;
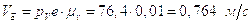 .
.
Найдём скорость точек D45, L из совместного решения 2-х уравнений:
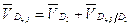 ,
,
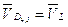 .
.
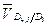 //BD и
//BD и 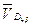 //L0L7. Второе
равенство вытекает из принадлежности точек одному звену (5), а значит
движущихся в одном направлении.
//L0L7. Второе
равенство вытекает из принадлежности точек одному звену (5), а значит
движущихся в одном направлении.
Построив план, получим:
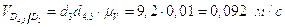 ;
;
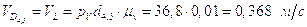 .
.
Определим угловые скорости звеньев. Угловые скорости звеньев определяются из следующих соотношений:
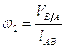 ,
, 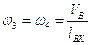 .
.
Подставим найденные значения линейных
скоростей 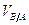 и
и 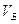 , а также известные
длины звеньев механизма
, а также известные
длины звеньев механизма 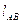 и
и 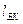 в
записанные формулы:
в
записанные формулы:
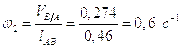 ,
,
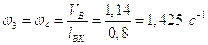 .
.
План ускорений для положения 3
Найдем ускорение точки A. Так
как ω1=const,
то угловое ускорение e1=0 и
тангенциальное ускорение 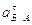 =0.
=0.
Полное ускорение точки A будет равно нормальному ускорению:
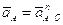 .
.
Вектор нормального ускорения 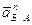 //ОА и направлен к центру
вращения звена 1.
//ОА и направлен к центру
вращения звена 1.
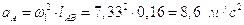
Примем масштаб построения плана ускорений:
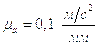 .
.
На плане ускорений:
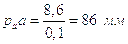 .
.
Выбираем точку-полюс плана
ускорений pа, проводим
вектор 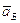 //ОА.
//ОА.
Определим ускорение точки B.
Ускорение точки B определим из совместного решения 2-х уравнений:
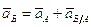 - для звена 2.
- для звена 2.
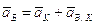 - для звена 3.
- для звена 3.
Решим первое уравнение:
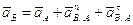 ,
,
где
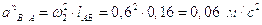 и
и 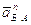 //ВA;
//ВA;
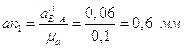 ;
;
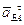
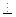 AВ.
AВ.
Решим второе уравнение:
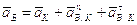 ,
,
где
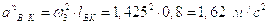 и
и 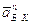 //ВK;
//ВK;
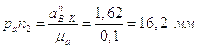 ;
;
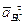
 ВK.
ВK.
Из плана получим:
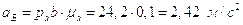 ;
;
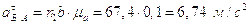 ;
;
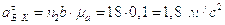 .
.
Найдем ускорение точки С.
Ускорение этой точки определим на основании свойства пропорциональности отрезков ac, аb на плане ускорений и размеров звеньев lAC, lАВ.
Получим следующее отношение:
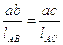 .
.
Отсюда находим:
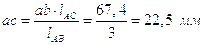 .
.
Построив план, получим:
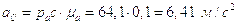 .
.
Найдем скорости точек D3, E.
Ускорения этих точек определим на основании свойства пропорциональности отрезков be, bd3, bk на плане ускорений и размеров звеньев lBE, lBD, lBK.
Получим следующее отношение:
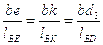 .
.
Отсюда находим:
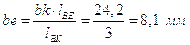 ;
;
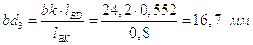 .
.
Построив план получим:
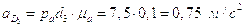 ;
;
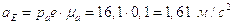 .
.
Определим ускорение точки D4,5.
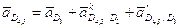 ,
,
где
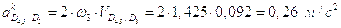 ;
;
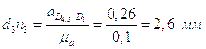
Для определения направления
ускорения 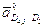 нужно вектор относительной скорости
нужно вектор относительной скорости 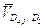 повернуть на угол
900 по направлению ω3.
повернуть на угол
900 по направлению ω3.
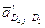 - релятивное ускорение, оно всегда направлено по
кулисе (векторы
- релятивное ускорение, оно всегда направлено по
кулисе (векторы 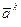 и
и 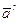 всегда взаимно перпендикулярны).
всегда взаимно перпендикулярны).
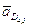 //L0L7.
//L0L7.
Построив план получим:
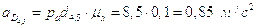 ;
;
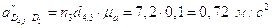 .
.
Угловое ускорения 2-го звена:
 .
.
Угловое ускорения 3-го звена:
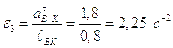 .
.
План скоростей для положения 0
Определим скорость ведущей точки механизма, т.е. точки звена, закон движения которого задан. В нашем случае это точка А звена 1:
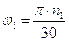 ,
,
где
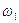 - угловая скорость
кривошипа,
- угловая скорость
кривошипа, 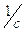 ;
;
n1 – частота
вращения звена 1, 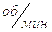 .
.

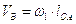 ,
,
где
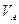 - скорость ведущей
точки механизма,
- скорость ведущей
точки механизма, 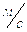 ;
;
lОА – длина кривошипа ОА, м.
Тогда:
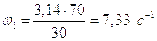 ;
;
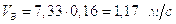 .
.
Примем масштаб построения плана скоростей:
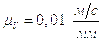 .
.
На плане скоростей:
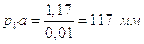 .
.
Выберем
произвольную точку-полюс плана скоростей 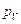 . Вектор
. Вектор 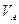 проведён перпендикулярно
кривошипу и направлен в сторону вращения звена 1(pVa).
проведён перпендикулярно
кривошипу и направлен в сторону вращения звена 1(pVa).
Скорость точки B может быть определена из совместного решения 2-х уравнений:
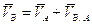 - для звена 2.
- для звена 2.
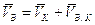 - для звена 3.
- для звена 3.
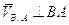 ,
, 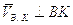 ,
,
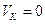 (неподвижная точка), следовательно
(неподвижная точка), следовательно 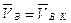 .
.
Строим план.
Построив план, получим:
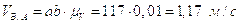 .
.
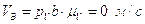 .
.
Найдем скорость точки С.
Скорость этой точки определим на основании свойства пропорциональности отрезков ac, аb на плане скоростей и размеров звеньев lAC, lАВ.
Получим следующее отношение:
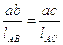 .
.
Отсюда находим:
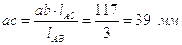 .
.
Построив план, получим:
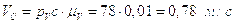 .
.
Найдем скорости точек D3, E.
Скорости этих точек определим на основании свойства пропорциональности отрезков be, bd3, bk на плане скоростей и размеров звеньев lBE, lBD, lBK.
Получим следующее отношение:
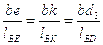 .
.
Отсюда находим:
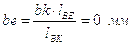 ;
;
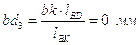 .
.
Построив план получим:
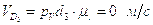 ;
;
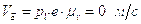 .
.
Найдём скорость точек D45, L из совместного решения 2-х уравнений:
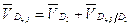 ,
,
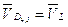 .
.
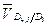 //BD и
//BD и 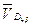 //L0L7. Второе равенство вытекает из принадлежности точек
одному звену (5), а значит движущихся в одном направлении.
//L0L7. Второе равенство вытекает из принадлежности точек
одному звену (5), а значит движущихся в одном направлении.
Построив план, получим:
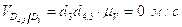 ;
;
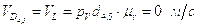 .
.
Определим угловые скорости звеньев. Угловые скорости звеньев определяются из следующих соотношений:
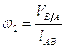 ,
, 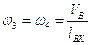 .
.
Подставим найденные значения линейных
скоростей 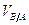 и
и 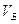 , а также известные
длины звеньев механизма
, а также известные
длины звеньев механизма 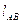 и
и 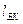 в
записанные формулы:
в
записанные формулы:
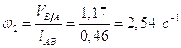 ,
,
 .
.
План ускорений для положения 0
Найдем ускорение точки A. Так
как ω1=const,
то угловое ускорение e1=0 и
тангенциальное ускорение 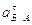 =0.
=0.
Полное ускорение точки A будет равно нормальному ускорению:
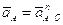 .
.
Вектор нормального ускорения 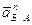 //ОА и направлен к
центру вращения звена 1.
//ОА и направлен к
центру вращения звена 1.
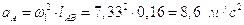
Примем масштаб построения плана ускорений:
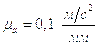 .
.
На плане ускорений:
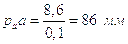 .
.
Выбираем точку-полюс плана
ускорений pа, проводим
вектор 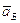 //ОА.
//ОА.
Определим ускорение точки B.
Ускорение точки B определим из совместного решения 2-х уравнений:
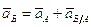 - для звена 2.
- для звена 2.
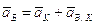 - для звена 3.
- для звена 3.
Решим первое уравнение:
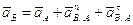 ,
,
где
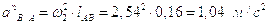 и
и 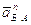 //ВA;
//ВA;
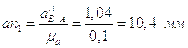 ;
;
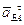
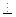 AВ.
AВ.
Решим второе уравнение:
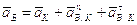 ,
,
где
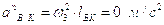 и
и 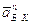 //ВK;
//ВK;
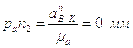 ;
;
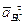
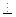 ВK.
ВK.
Из плана получим:
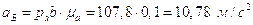 ;
;
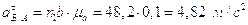 ;
;
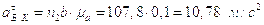 .
.
Найдем ускорение точки С.
Ускорение этой точки определим на основании свойства пропорциональности отрезков ac, аb на плане ускорений и размеров звеньев lAC, lАВ.
Получим следующее отношение:
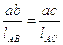 .
.
Отсюда находим:
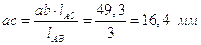 .
.
Построив план, получим:
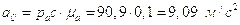 .
.
Найдем скорости точек D3, E.
Ускорения этих точек определим на основании свойства пропорциональности отрезков be, bd3, bk на плане ускорений и размеров звеньев lBE, lBD, lBK.
Получим следующее отношение:
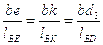 .
.
Отсюда находим:
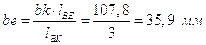 ;
;
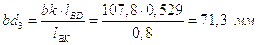 .
.
Построив план получим:
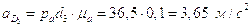 ;
;
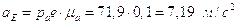 .
.
Определим ускорение точки D4,5.
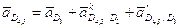 ,
,
где
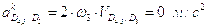 ;
;
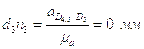
Для определения направления
ускорения 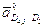 нужно вектор относительной скорости
нужно вектор относительной скорости 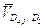 повернуть на угол
900 по направлению ω3.
повернуть на угол
900 по направлению ω3.
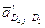 - релятивное ускорение, оно всегда направлено по
кулисе (векторы
- релятивное ускорение, оно всегда направлено по
кулисе (векторы 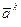 и
и 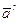 всегда взаимно перпендикулярны).
всегда взаимно перпендикулярны).
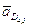 //L0L7.
//L0L7.
Построив план получим:
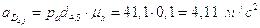 ;
;
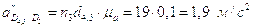 .
.
Угловое ускорения 2-го звена:
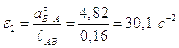 .
.
Угловое ускорения 3-го звена:
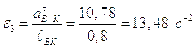 .
.
1.3. Силовой расчёт
Силовой анализ проведём по методике изложенной в [2, с. 3-22.]
Целью силового расчёта является определение усилий, действующих на звенья механизма (внешние силы), давлений (реакций) в кинематических парах (внутренние силы), приложенного к начальному механизму, определение коэффициента полезного действия механизма.
Силовой расчёт механизма может быть выполнен различными методами.
В данной работе силовой расчёт механизма выполняется для одного положения рабочего хода, для которого определены ускорения.
Силовому расчёту предшествует структурный и
кинематический анализиз.
1.3.1. Силы,
действующие на звенья механизма
Рабочим звеном данного механизма,
является звено 5, к которому приложено полезное сопротивление 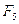 . Помимо силы
. Помимо силы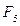 , учтём также силы тяжести и инерции, а также моменты
инерции звеньев.
, учтём также силы тяжести и инерции, а также моменты
инерции звеньев.
Массы звеньев:
Для звена 1 (кривошип)
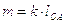 ,
, 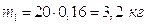 .
.
Для звена 2 (шатун)
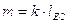 ,
, 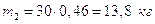 .
.
Для звена 3 (кулиса)
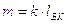 ,
, 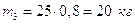 .
.
Для звена 4 (камень кулисы)
Массой камня кулисы m4 пренебрегаем, так как она мала по сравнению с массами остальных звеньев.
Для звена 5 (ползун)
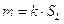 ,
, 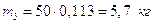 .
.
Вычислим
вес звеньев механизма: 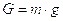 ,
,
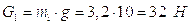 ;
;
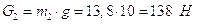 ;
;
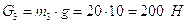 ;
;
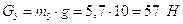 .
.
Силы
инерции звеньев: 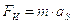 ,
,
где aS1, aS2 aS3, aS5 – ускорения центров масс, определимые из плана ускорений.
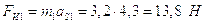
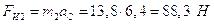
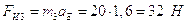
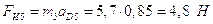 ,
,
Главные
моменты сил инерции: 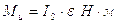 ,
,
где IS - момент
инерции массы звена относительно оси, проходящей через центр масс (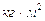 );
); 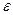 - угловое ускорение
звена (с-2), определяется из ранее проведенных кинематических
исследований.
- угловое ускорение
звена (с-2), определяется из ранее проведенных кинематических
исследований.
Массы и моменты инерции массы звена находим по [2, стр. 22-23]
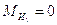 , так как при
, так как при 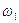 =const,
=const, 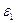 =0;
=0;
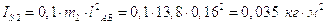 ;
;
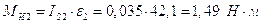 ;
;
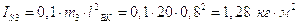
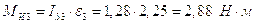 ;
;
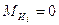 , так как при горизонтальном движении звена 5
, так как при горизонтальном движении звена 5 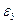 =0.
=0.
Моменты сил инерции направлены противоположно угловым ускорениям.
1.3.2. Силовой расчёт группы 4-5 [П3.4 -В4.5-П0.5]
К звеньям группы приложены:
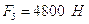 – сила полезного сопротивления
– сила полезного сопротивления
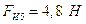 - сила инерции звена 5
- сила инерции звена 5
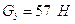 - сила тяжести
звена 5
- сила тяжести
звена 5
R05 и R34 – реакции во внешних кинематических парах
Уравнение равновесия группы в форме сил запишется:
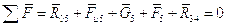 .
.
Примем
масштаб построения: 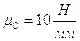 /
/
В точке D звена будет приложена реакция R3.4 перпендикулярная к звену 3, которую найдём из плана сил:
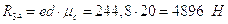 .
.
Из плана найдем величину реакции заделки:
 .
.
Уравнение равновесия звена 4:
 .
.
Из уравнения находим:
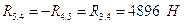 .
.
1.3.3. Силовой расчёт группы 2-3 [В1.2 -В2.3-В0.3]
К звеньям группы приложены:
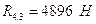 - давление в кинематической паре от звена 4;
- давление в кинематической паре от звена 4;
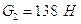 - сила тяжести звена 2;
- сила тяжести звена 2;
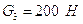 - сила тяжести
звена 3;
- сила тяжести
звена 3;
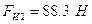 - сила инерции звена 2;
- сила инерции звена 2;
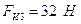 - сила инерции звена 3;
- сила инерции звена 3;
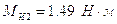 – момент инерции звена 2;
– момент инерции звена 2;
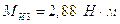 – момент инерции звена 3.
– момент инерции звена 3.
Эти внешние силовые факторы, известные по величине, по направлению и точкам приложения.
Уравнение равновесия группы в форме сил запишется:
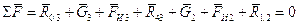 ,
,
где 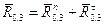 ,
, 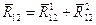 .
.
Из
уравнения равновесия второго звена найдем 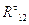 :
:
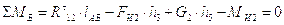 ;
;
Размеры плеч:
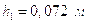 ;
;

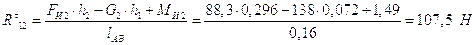 .
.
Из
уравнения равновесия третьего звена найдем 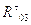 :
:
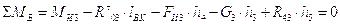 .
.
Размеры плеч:
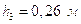 ;
;
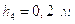
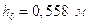
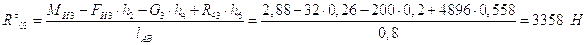
Уравнение равновесия группы примет вид:
 .
.
Примем масштаб построения:
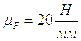 .
.
Из плана находим:
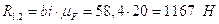 ;
;
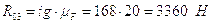 ;
;
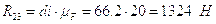 .
.
1.3.4. Силовой расчёт начального механизма В01
Начальным механизмом является кривошип 1.
К кривошипу 1 приложены силы:
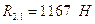 - реакция со стороны звена 2
- реакция со стороны звена 2
G1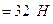 - сила тяжести звена 1
- сила тяжести звена 1
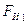
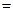
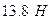 - сила инерции звена 1
- сила инерции звена 1
Уравновешивающую силу найдем из уравнения:
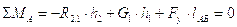 .
.
Здесь h1=0,08м, h2=0,16м.
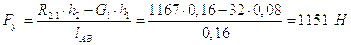 .
.
Давление R01 в кинематической паре В0.1 определяется из условия равновесия звена 1:
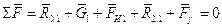 .
.
Примем масштаб построения:
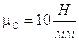 .
.
Из
плана найдем величину реакции 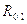 :
:
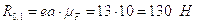 .
.
1.3.5. Определение величины уравновешивающей силы методом
рычага Н.Е. Жуковского
Этот метод позволяет определить величину уравновешивающей силы без определения реакции в КП, то есть без выполнения силового расчёта групп Ассура.
Для этого необходимо план скоростей повернуть на 90 градусов,
принимаемый как твёрдое тело, с неподвижной точкой в полюсе, к концам векторов
одноимённых точек которого, приложены внешние силы, в этом числе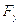 .
.
Заменим моменты сил инерции парами сил:
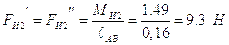 ;
;
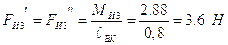 .
.
Запишем уравнение равновесия:
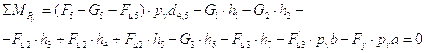
Плечи сил определим непосредственно из чертежа:
|
h1=117 мм; h2=230 мм; h3=34 мм; h4=5 мм; h5=50 мм; |
h6=148 мм; h7=114 мм; pVb=229 мм; pVа=234 мм; pVd4,5=73,7 мм. |
Величину уравновешивающей силы, полученной методом рычага Н.Е. Жуковского найдем из записанного уравнения равновесия:
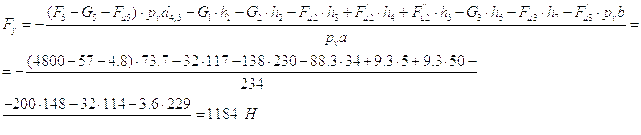 Расхождение в
значениях величины уравновешивающей силы, полученных из плана сил и “рычага”
Жуковского, определяемые по формуле:
Расхождение в
значениях величины уравновешивающей силы, полученных из плана сил и “рычага”
Жуковского, определяемые по формуле:
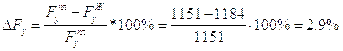 .
.
Кафедра теоретической и прикладной механики
КУРСОВОЙ ПРОЕКТ ПО ТЕОРИИ МЕХАНИЗМОВ И МАШИН
Студенту 150700 «Машиностроение» факультета, гр. З-8Л31/21
Толстоброву Антону Анатольевичу
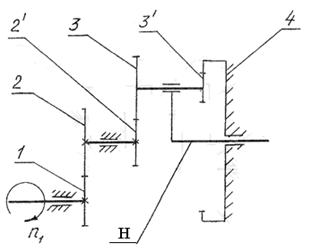
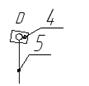
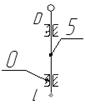
ЗУБЧАТЫЙ МЕХАНИЗМ
Синтез, анализ зубчатого механизма и профилирование зацепления
Задание №606
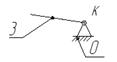
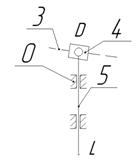
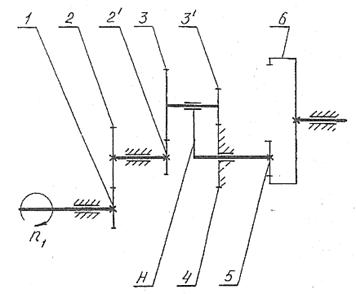 |
Схема механизма
 Исходные данные:
Исходные данные:
Передаточное число U1.6 = 350
Число сателлитов k = 3-4
Модули зацепления m1,2,5,6 =4 мм
m2’,3,3’,4 =1 мм
Частота вращения ведущего звена n = 2000 об/мин
Дополнительные условия
Дата выдачи задания: 10.06.2016
Срок выполнения: 5 месяцев
Руководитель: Горбенко Михаил Владимирович
2. Зубчатый механизм
2.1 Введение
Целью данной работы является приобретение навыков в подборе чисел зубьев планетарного механизма, геометрического расчета зубчатого эвольвентного зацепления, кинематического исследования зубчатого механизма
По данным задания необходимо:
1. Произвести разбивку передаточного отношения сложного зубчатого механизма по ступеням и подобрать числа зубьев зубчатых колес, удовлетворяющим требуемому передаточному отношению, условиям соосности, сборки и соседства(для планетарной ступени). Размеры механизма должны быть минимальными
2. Определить основные геометрические параметры всех зубчатых колёс механизма(если число зубьев зубчатого колеса меньше 17, то такое колесо должно быть нарезано со смещением режущего инструмента).
3. Определить числа оборотов всех звеньев механизма аналитическим и графическими способами, для чего вычертить механизм в масштабе, построить картину линейных и диаграмму угловых скоростей звеньев. Результаты определения передаточных отношений и чисел зубьев аналитическим и графическим способами сравнить, определить величину ошибки.
4. Провести полный геометрический расчёт одного и того же эвольвентного зацепления зубчатых колёс, нарезанных со смещением режущего инструмента (А) и без (Б – нулевые колёса). Результаты расчёта геометрических параметров зубчатых колёс свести в таблицу
5. По данным расчёта пункта IV провести профилирование зацеплений А и Б,
при этом:
а) построить профили не менее трех – четырех зубьев на каждом колесе;
б) найти теоретические и действительные линии зацепления;
в) найти дуги зацепления (действительные);
г) найти и выделить рабочие участки профилей зубьев;
д) построить диаграмму удельного скольжения и удельного давления на профилях зубьев;
е) определить коэффициенты перекрытия графическим методом (результаты сравнения с коэффициентами перекрытия полученные аналитическим способом);
ж) дать анализ по результатам профилирования корригированного зацепления: дать качественную и количественную оценку изменений размеров зубьев и показателей зацепления, нарезанных со смещением (корригированных) зубчатых колёс по сравнению с не корригированными колёсами нулевого зацепления.
6. определить КПД всего механизма (КПД, одной пары зубчатых колёс принять 0,98)
2.2. Разбивка передаточного отношения по ступеням
Данный механизм состоит из трех ступеней:
Первая ступень – зубчатая передача внешнего зацепления, состоящая из зубчатых колес 1 и 2;
Вторая ступень – планетарная зубчатая передача вида АА, состоит из зубчатых колес 2", 3,3’,4 и водила Н;
Третья ступень – зубчатая передача внутреннего зацепления, состоящая из зубчатых колес 5 и 6;
Передаточное отношение всего механизма определим как произведение всех передаточных чисел механизма:
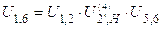 ;
;
где
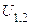 - передаточное
отношение рядового механизма
- передаточное
отношение рядового механизма
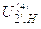 - передаточное отношение планетарного механизма AА;
- передаточное отношение планетарного механизма AА;
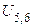 - передаточное отношение
рядового механизма.
- передаточное отношение
рядового механизма.
При условии 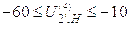 ,
примем передаточное отношение планетарного механизма
,
примем передаточное отношение планетарного механизма 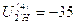 . Примем
. Примем 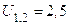 ,
, 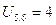
2.3. Подбор чисел зубьев зубчатых колес
Подберем число зубьев
зубчатых колес, удовлетворяющих требуемому отношению, условию соосности, сборки
и соседства по методу сомножителей. Так как передача осуществляется от колеса 2’ к водилу Н и задано передаточное отношение 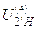 ,
то передаточное отношение обращенного механизма определим по формуле:
,
то передаточное отношение обращенного механизма определим по формуле:
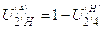 ;
;
Подставив
в эту формулу полученное 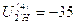 ,
получим:
,
получим:
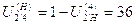
Заменим числа зубьев пропорциональными им коэффициентами С, тогда
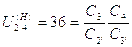
Запишем в таблицу 8 все возможные варианты разложения 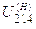 на сомножители
виде дроби
на сомножители
виде дроби 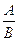 , где B =1 и
варианты разложения с помощью дополнительных множителей учитывая рекомендации.
, где B =1 и
варианты разложения с помощью дополнительных множителей учитывая рекомендации.
Таблица 8
|
№ варианта |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
|
|
|
|
|
|
|
|
|
|
|
В соответствии с рекомендациями пределами отношения
сомножителей при которых выполняется условие соседства смежных сателлитов  исключаем из
рассмотрения 2,4,5,7,8,10 варианты.
исключаем из
рассмотрения 2,4,5,7,8,10 варианты.
Определим P, Q и P+Q по формуле:
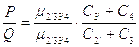 ,
,
где значение С2’, С3, С3’, С4 берутся из таблицы 8 для соответствующего варианта.
Полученные значения запишем в таблицу 9.
Таблица 9
|
1 |
3 |
6 |
9 |
|
|
Р |
10 |
10 |
20 |
10 |
|
Q |
45 |
5 |
5 |
15 |
|
P+Q |
55 |
15 |
25 |
25 |
Из таблицы следует, что минимальную сумму P+Q имеет вариант 1.
Определим числа зубьев зубчатых колёс для варианта 9 по формуле:
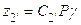 ;
; 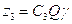 ;
;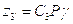 ;
; 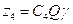 .
.
Подставив значения С2’=3, С3=12,
С3’I=1, С4=9, Р=10, Q=15 и приняв
значение 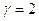 получим:
получим:
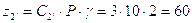 ;
;
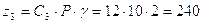 ;
;
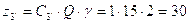 ;
;
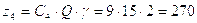 .
.
Определяем габариты 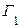 и
и 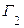
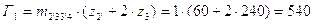 мм;
мм;
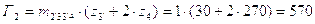 мм;
мм;
Проверка передаточного отношения.
Проверяем
выполнение заданного 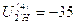 при
принятом числе зубьев по формуле:
при
принятом числе зубьев по формуле:
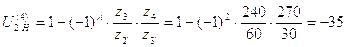 ,
,
где n – число пар колес внешнего зацепления n =2
Заданное передаточное отношение выполняется.
Проверка выполнения условия соосности.
Проверяем выполнение условия соосности по формуле:
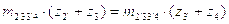
1(60+240)=1(30+270)
300=300
Условие соосности выполняется.
Проверка условия сборки.
Проверяем условие сборки по формуле:
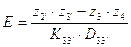 ,
,
где К3.3’=3 (число сателлитов), D3.3’=30 (наибольший общий делитель зубьев Z3 и Z3’ )
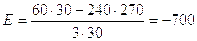 - целое число
- целое число
Условие сборки выполняется.
Поскольку выполнены рекомендации, то условие соседства можно не проверять.
2.4. Геометрический расчёт внешнего эвольвентного зацепления
Для зубчатых колёс 1,2 выполняется полный геометрический расчёт, который приведен в таблице 3. Коэффициенты смещения приняты из условия износостойкости.
Геометрические параметры внешнего эвольвентного зацепления цилиндрических прямозубых колёс, нарезанных инструментом реечного типа.
Таблица 10
Исходные данные |
|||||||||||
Параметры |
Обозначение |
Величина |
|||||||||
|
Число зубьев |
шестерни |
Z1 |
12 |
||||||||
|
колеса |
Z2 |
30 |
|||||||||
|
Модуль зацепления, мм |
m |
4 |
|||||||||
|
Исходный контур по ГОСТ 13755 – 68 |
Угол профиля, град |
|
20 |
||||||||
|
Коэффициент высоты головки |
|
1 |
|||||||||
|
Коэффициент радиального зазора |
С1 |
0,25 |
|||||||||
|
Коэффициент радиуса кривизны переходной кривой |
|
0,38 |
|||||||||
Коэффициент смещения |
А |
X1 |
0.3 |
||||||||
|
X2 |
0.93 |
||||||||||
|
Б |
X1 |
0 |
|||||||||
|
X2 |
0 |
||||||||||
Р А С Ч Е Т |
|||||||||||
|
Наименование параметра |
Формула |
А |
Б |
||||||||
|
1 |
Передаточное число |
|
2.5 |
2.5 |
|||||||
|
2 |
Эвольвентный угол в точке на делительной окружности, град. |
|
|
||||||||
|
|
|||||||||||
|
3 |
Эвольвентный угол в точке на начальной окружности, град. |
|
0,0364218 |
||||||||
|
4 |
Угол зацепления, град. |
|
|
0,4837 |
0.364 |
||||||
|
|
|
0,9002 |
0.9397 |
||||||||
|
5 |
Делительный шаг зубьев |
|
12,566 |
12,566 |
|||||||
|
6 |
Основной шаг зубьев, мм |
|
11,809 |
11,809 |
|||||||
|
7 |
Начальный шагЗубьев, мм |
|
13,118 |
12,566 |
|||||||
|
8 |
Межосевое расстояние, мм |
|
88 |
84 |
|||||||
|
9 |
Радиус делительной окружности, мм |
|
24 60 |
24 60 |
|||||||
|
10 |
Радиус основной окружности, мм |
|
22,553 56,382 |
22,553 56,382 |
|||||||
|
11 |
Радиус начальной окружности, мм |
|
25,053 |
24 |
|||||||
|
62,632 |
60 |
||||||||||
|
12 |
Радиус окружности впадин, мм |
|
20,2 58,72 |
19 55 |
|||||||
|
13 |
Радиус окружности вершин, мм |
|
28,28 66,8 |
28 64 |
|||||||
|
14 |
Угол профиля на окружности вершин, град |
|
36,97 0,753 33,287 0,6565 |
36,35 0,736 29,842 0,5737 |
|||||||
|
15 |
Эвольвентный угол в точке на окружности вершин, град |
|
0,10785 0,075581 |
0,101653 0,052835 |
|||||||
|
16 |
Толщина зуба по дуге делительной окружности, мм |
|
7,157 8,991 |
6,283 6,283 |
|||||||
|
17 |
Толщина зуба по дуге основной окружности, мм |
|
7,397 10,129 |
6,577 7,585 |
|||||||
|
18 |
Толщина зуба по дуге начальной окружности, мм |
|
6,402 6,715 |
6,283 6,283 |
|||||||
|
19 |
Толщина зуба по дуге окружности вершин, мм |
|
3,176 1,903 |
2,472 1,847 |
|||||||
|
20 |
Высота зуба, мм |
|
8,08 |
9 |
|||||||
|
21 |
Глубина захода, мм |
|
7,08 |
8 |
|||||||
|
22 |
Показатель заострения |
|
0,794 0,476 |
0,618 0,462 |
|||||||
|
23 |
Коэффицент воспринемаемого смещения |
|
0,921 |
0 |
|||||||
|
24 |
Воспринемаемое смещение |
|
3,684 |
0 |
|||||||
|
25 |
Коэффицент уравнительного смещения |
|
0,309 |
0 |
|||||||
|
26 |
Радиус кривизны переходной кривой, мм |
|
1,52 |
1,52 |
|||||||
|
26| |
Радиальный зазор мм |
|
1 |
1 |
|||||||
|
27 |
Коэффициент перекрытия |
Аналитически |
|
1,34 |
1,71 |
||||||
|
По чертежу |
lp1p2 e = lp1p2 / pb ( lp1p2 – длина активной части линии зацепления ) |
1,21 |
1,71 |
||||||||
2.5. Расчёт качественных показателей зацепления
К качественным показателям зацепления относятся
коэффициент перекрытия e, показывающий,
сколько пар зубьев одновременно находятся в зацеплении, коэффициент удельного
скольжения 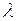 и удельного
давления
и удельного
давления 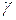 . Удельное
скольжение является показателем износостойкости, а удельное давление характеризует
контактную прочность. Чем меньше значения этих коэффициентов, тем выше
износостойкость и контактная прочность зубчатых колёс.
. Удельное
скольжение является показателем износостойкости, а удельное давление характеризует
контактную прочность. Чем меньше значения этих коэффициентов, тем выше
износостойкость и контактная прочность зубчатых колёс.
2.5.1 Расчёт коэффициента удельного скольжения
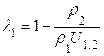 ,
, 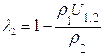 .
.
Здесь 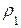 и
и 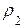 - радиусы кривизны
эвольвент профилей зубьев колёс 1 и 2.
- радиусы кривизны
эвольвент профилей зубьев колёс 1 и 2.
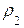 +
+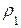 =
е =N1 N2 – длинна теоретической линии зацепления.
=
е =N1 N2 – длинна теоретической линии зацепления.
Обозначим 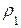 =
= 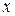 , тогда
, тогда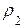 = e -
= e - 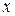 .
.
Формулы удельного скольжения примут вид, удобной для выполнения расчётов.
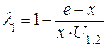 ,
, 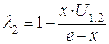 .
.
2.5.2 Расчёт коэффициента удельного давления
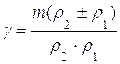 ,
,
где m – модуль зацепления; знак «+» для внешнего, знак «-» для внутреннего зацепления.
Выражая, 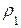 и
и 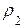 через e и
через e и 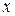 , получим:
, получим:
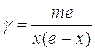 .
.
Значения величин удельного скольжения и удельного давления для зацеплений А и В приведены в таблицах 11 и 12.
Значения величин удельного скольжения и удельного давления для неравносмещенного зацепления (А)
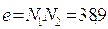
Таблиц 11
|
N1 |
P2 |
П |
P1 |
N2 |
|||||
|
х |
0 |
2 |
3,1 |
11,2 |
14 |
16,6 |
23 |
31 |
38,9 |
|
е-х |
38,9 |
36,9 |
35,8 |
27,7 |
24,9 |
22,3 |
15,9 |
7,9 |
0 |
|
|
|
-6,38 |
-4,62 |
0 |
0,289 |
0,463 |
0,723 |
0,898 |
1 |
|
|
1 |
0,864 |
0,783 |
0 |
-0,406 |
-0,861 |
-2,616 |
-8,81 |
|
|
|
|
2,108 |
1,402 |
0,502 |
0,446 |
0,42 |
0,42 |
0,635 |
|
Значения величин удельного скольжения и удельного давления для нулевого зацепления (Б).
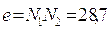
Таблица 12
|
N1 |
|
П |
P1 |
N2 |
|||||
|
х |
0 |
3 |
6 |
8,2 |
12 |
16,6 |
20 |
25 |
28,7 |
|
e-х |
28,7 |
25,7 |
22,7 |
20,5 |
16,7 |
12,1 |
8,7 |
3,7 |
0 |
|
|
|
-2,427 |
-0,513 |
0 |
0,443 |
0,708 |
0,826 |
0,941 |
1 |
|
|
1 |
0,708 |
0,339 |
0 |
-0,796 |
-2,43 |
-4,747 |
-15,892 |
|
|
|
- |
1,489 |
0,843 |
0,683 |
0,571 |
0,571 |
0,66 |
1,241 |
+ |
2.5.3 Коэффициент полезного действия
Коэффициент полезного действия (КПД) является важным показателем качества планетарного механизма. Он может быть вычислен приближённо по формулам, приведённым в таблице 3 стр.12 методическое пособие «Кинематический синтез типовых планетарных механизмов».
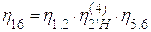 ,
,
где
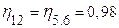
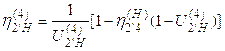
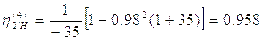
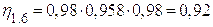
2.6 Определение частоты вращения всех звеньев механизма
Частота вращения ведущего звена:
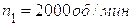 .
.
Частота вращения второго звена:
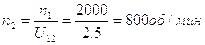
Частота вращения водила:
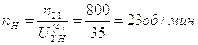
Частота вращения пятого звена:
n5=nH=23 об/мин.
шестого звена:
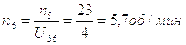
Частота вращения сателлитов:
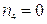 ,так как колесо неподвижное
,так как колесо неподвижное
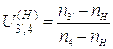 ,
,
где 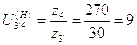 .
.
Тогда
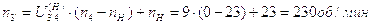
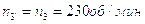 .
.
2.7 Анализ по результатам профилирования
Анализ на основании расчётов и по результатам профилирования зацепления:
1. Число зубьев шестерни z1=12 меньше zmin=17, то при нарезании методом обкатки без смещения инструментом реечного типа будет иметь место явления подреза.
2. При положительном смещении толщина зуба у его основания увеличивается, что приводит к увеличению изгибной прочности зуба. Так, в нашем случае толщина зуба шестерни в опасном сечении при х1=0 была аБ=6,58 мм, то стала аА=7,56 мм, т.е. увеличилась в 7,56/6,58=1,15 раза, что приведёт к увеличению изгибной прочности в (1,15) 2=1,32 раза.
3. Удельное скольжение на ножках зубьев в точках P1 и P2 изменилось следующим образом:
в точке P1 : 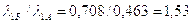 ;
;
Уменьшение удельного скольжения скажется на пропорциональном повышении износостойкости зубьев.
4.
Удельное давление в полюсе
зацепления (зона однопарного зацепления) также уменьшилось
в
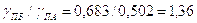
что приводит к повышению контактной прочности в 1,36 раза.
5. Наряду с этими положительными изменениями показателей зацепления, имеют место и ухудшение показателей. К числу таких показателей следует отнести уменьшение коэффициента перекрытия (1,21 против 1,34) и заострение зубьев.
Томский политехнический университет
Кафедра теоретической и прикладной механики
КУРСОВОЙ ПРОЕКТ ПО ТЕОРИИ МЕХАНИЗМОВ И МАШИН
Студенту 150700 «Машиностроение» факультета, гр. З-8Л31/21
Толстоброву Антону Анатольевичу
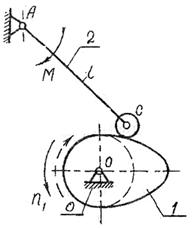
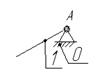
КУЛАЧКОВЫЙ МЕХАНИЗМ
Определение наименьшего размера и построение профиля кулачка
Задание №606
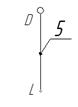
Схема механизма Закон движения толкателя по углу
 поворота
(перемещения) кулачка
поворота
(перемещения) кулачка
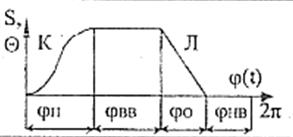
Исходные данные:
Угол поворота толкателя θ =320
Длина коромысла l =125 мм
Минимальные углы передачи движения:
при подъеме 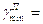 500
500
при опускании 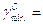 300
300
Полезный момент сопротивления на коромысле М =550 Нм
Частота вращения кулачка n = 55 об/мин
Дополнительные условия
Дата выдачи задания: 10.06.2016
Срок выполнения: 5 месяцев
Руководитель: Горбенко Михаил Владимирович
3.1. Масштабы графиков движения кулачка
Вычерчивается в масштабе график: Sc=Sc(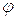 ).
).
Для коромыслового толкателя линейное перемещение точки С конца толкателя:
Sc=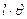 мм,
мм,
где L - длина коромысла, мм,
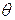 - размах (ход)
коромысла в радианах:
- размах (ход)
коромысла в радианах:
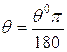 .
.
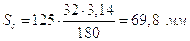 .
.
В зависимости от формата выбираем
линейный масштаб перемещения 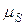 (мм/мм).
Тогда высота графика h при
(мм/мм).
Тогда высота графика h при 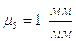 будет:
будет:
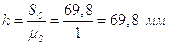 .
.
Этот график одновременно будет
являться и графиком углового перемещения коромысла 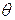 по углу поворота
кулачка т. е.
по углу поворота
кулачка т. е. 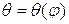 в
масштабе:
в
масштабе:
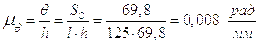 .
.
Масштабы по оси абсцисс:
угловой масштаб 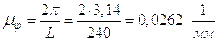 .
.
При заданной частоте вращения кулачка n об/мин масштаб времени:
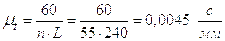 ,
,
где L – длина графика S - 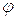 (принимается в
зависимости от формата чертежа).
(принимается в
зависимости от формата чертежа).
3.2. Масштабы графиков первой производной
Масштаб перемещения толкателя на графике Z-S. Принимаем:
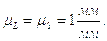 .
.
Принимаем первое полюсное расстояние:
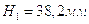 .
.
Методом графического дифференцирования (метод касательных или метод хорд) строятся графики первой производной
Масштабы графиков:
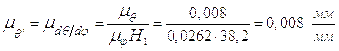 .
.
Масштаб угловой скорости этих графиков определяется из выражений:
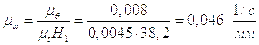 .
.
1. По заданным давления или передачи движения находится область возможных положений центра вращения кулачка и определяются размеры кулачкового механизма: радиус кулачка, величина смещения, расстояние между центрами вращения кулачка и коромысла.
2. При выбранных размерах кулачка и заданному закону движения толкателя, используя метод обращения движения, строится теоретический профиль кулачка.
3. Выбрав (определив) радиус ролика rp строим практический профиль кулачка.
3.3. Масштабы графиков второй производной
1. Для определения
линейного или углового ускорения строим график: а=а(t) или 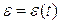 ,
для чего следует продифференцировать график V=V(t) или
,
для чего следует продифференцировать график V=V(t) или 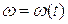 . Масштабы этих
графиков будут:
. Масштабы этих
графиков будут:
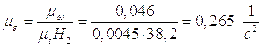
Здесь 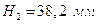 - полюсное
расстояние при вторичном дифференцировании. Масштабы аналогов ускорений:
- полюсное
расстояние при вторичном дифференцировании. Масштабы аналогов ускорений:
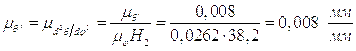 .
.
2. Выбрав положение центра
вращения кулачка (в области возможных его положений) и, соединив его с концами
отрезков на графиках, определяются углы передачи движения 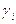 и строится график
и строится график 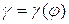 .
.
3.4.
Определение минимального радиуса кулачка 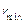
Из плана находим:
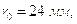
Радиус ролика:
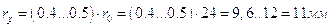 ,
,
3.5. Силовой расчёт
Для дальнейшего расчёта
на прочность деталей кулачкового механизма выполняем силовой расчёт –
определяем силы действующие на звенья механизма, реакции в кинематических парах
(R0.1 R1.2 R0.2) и величину уравновешивающего
момента (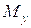 ), приложенного к
кулачку.
), приложенного к
кулачку.
Уравнение равновесия коромысла в виде моментов будет:
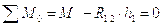
Из плана находим величину плеча:
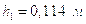 ;
;
Находим неизвестную реакцию:
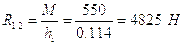
Уравнение равновесия коромысла в виде сил будет:
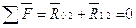
Строим план сил в масштабе 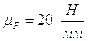 .
.
Из плана находим:
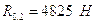
Уравнение равновесия кулачка в виде сил запишется в виде:
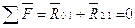
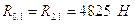
Уравнение равновесия кулачка в виде моментов будет:
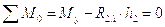
Из плана находим величину плеча:
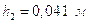 ;
;
Уравновешивающий момент равен:
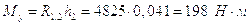
Заключение.
При внешнем эвольвентном нулевом зацеплении колёс в данном случае мы имеем подрез ножки зубьев шестерни. График удельного скольжения и график удельного давления неравномерны, что говорит о резкой смене напряжения на зубья, находящиеся в зацеплении. Скольжение же профилей влияет на износ зубьев, уменьшая износостойкость передачи. Чтобы избежать больших потерь на скольжение профилей и уменьшить их износ, практическая линия зацепления должна располагаться в зоне относительно коэффициентов скольжения. Так как при подрезе срезается часть эвольвенты, образующей профиль зуба, то ножки зубьев ослабляются. Чтобы уменьшить подрез ножки зуба вводится смещение, определяемое коэффициентом смещения х. Так же меняется межосевое расстояние, которое не влияет на передаточное отношение, а влияет на положение полюса зацепления и величину угла зацепления.
Одним из основных достоинств кулачковых механизмов является лёгкость синтеза, то есть получения профиля кулачка с большой степенью точности, удовлетворяющему заданному закону движения толкателя. В кулачковом механизме легко осуществить движение ведомого звена-толкателя с остановками, при непрерывном движении кулачка.
Недостатком является повышенное удельное давление а, следовательно, повышенный износ элементов высшей кинематической пары, что в свою очередь, приводит к искажению закона движения толкателя. Также кулачковый механизм обладает низким КПД, вследствие увеличения угла давления. При КПД примерно равном нулю, кулачковый механизм может заклиниваться. Тогда для устранения возможности заклинивания, ставится условие, чтобы угол давления во всех положениях механизма был меньше критического, при котором КПД=0.
Литература
|
1. 2. 3. 4. 5. |
Горбенко В.Т. Теория механизмов и машин. Содержание и методические указания по выполнению курсового проекта. –Томск: ТПИ,1988. Горбенко В.Т. Силовой расчёт рычажных механизмов. Методические указания по выполнению курсового проекта. –Томск: ТПИ,1988. И.И. Артоболевский. Теория механизмов и машин. –М.: Наука, 1975. Ливитский Н.И. Теория механизмов и машин. –М.: Наука,1979. Кореняко А.С., Кременштейн Л.И. и др. Курсовое проектирование по теории механизмов и машин. –Киев: Высшая школа, 1970. |














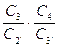
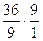
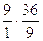
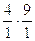
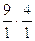
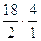
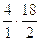
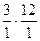
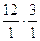
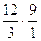
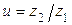
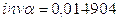
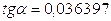
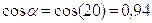
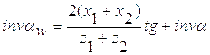
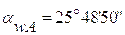
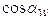
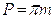
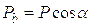

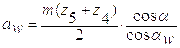
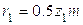
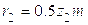
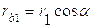
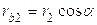
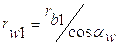
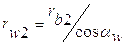
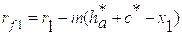
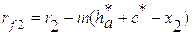
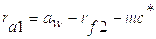
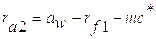
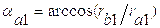
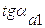
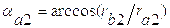
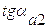
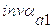
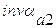
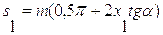
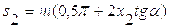
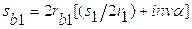
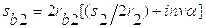
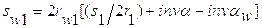
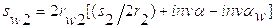
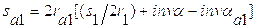
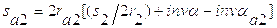
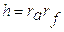
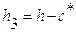
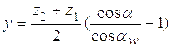
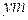
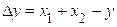
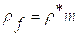
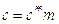
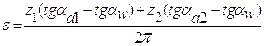
 (zip - application/zip)
(zip - application/zip)










