БУ ВО

«СУРГУТСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

Политехнический институт

Кафедра информатики и вычислительной техники

Очное отделение

РЕФЕРАТ

по дисциплине «Специальные главы математики»

на тему «Численные методы оптимизации».

Сургут, 2015

Содержание

Введение. 3

1. Общая характеристика методов. 4

2. Метод Ньютона. 6

3. Метод ветвей и границ. 7

4. Метод наискорейшего градиентного спуска. 11

Заключение. 15

Список литературы. 16

Введение.

При решении конкретной задачи оптимизации исследователь прежде всего должен выбрать математический метод, который приводил бы к конечным результатам с наименьшими затратами на вычисления или же давал возможность получить наибольший объем информации об искомом решении. Выбор того или иного метода в значительной степени определяется постановкой оптимальной задачи, а также используемой математической моделью объекта оптимизации.

Оптимизация в широком смысле слова находит применение в науке, технике и в любой другой области человеческой деятельности. Оптимизация – целенаправленная деятельность, заключающаяся в получении наилучших результатов при соответствующих условиях.

Поиски оптимальных решений привели к созданию специальных математических методов и уже в 18 веке были заложены математические основы оптимизации (вариационное исчисление, численные методы и др.). Однако до второй половины 20 века методы оптимизации во многих областях науки и техники применялись очень редко, поскольку практическое использование математических методов оптимизации требовало огромной вычислительной работы, которую без ЭВМ реализовать было крайне трудно, а в ряде случаев – невозможно.

Особенно большие трудности возникали при решении задач оптимизации из-за большого числа параметров и их сложной взаимосвязи между собой. При наличии ЭВМ ряд задач оптимизации поддается решению.

1. Общая характеристика методов.

При решении конкретной задачи оптимизации исследователь прежде всего должен выбрать математический метод, который приводил бы к конечным результатам с наименьшими затратами на вычисления или же давал возможность получить наибольший объем информации об искомом решении.

Классификация методов оптимизации (по числу параметров):

    - одномерная оптимизация;

    - многомерная оптимизация.

Рассмотрим три известных метода одномерной оптимизации:

1. Метод дихотомии (деления отрезка пополам).

Этот метод является аналогом известного метода дихотомии (половинного деления) отыскания решения уравнения F(x) = 0 на отрезке и выглядит так. Обозначим через Lⁿ = [aⁿ, bⁿ] отрезок, получающийся на n-ом шаге (естественно, L⁰ = [a, b]). Переход от Lⁿ к Lⁿ⁺¹ сводится к размещению на Lⁿ двух пробных точек xⁿ и yⁿ так, чтобы расстояние между ними было равно ε и они были симметричны относительно центра отрезка:

 , 

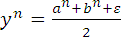
и выбору в качестве Lⁿ⁺¹ отрезка [aⁿ, yⁿ], если f(xⁿ) ≤ f(yⁿ) и [xⁿ, bⁿ] в противном случае. Таким образом, каждый шаг требует двух вычислений функции и за n вычислений (n четно) мы получаем отрезок неопределенности длины

где l = b–a — длина начального отрезка.

2. Метод Фибоначчи.

В силу того, что в асимптотике , метод золотого сечения может быть трансформирован в так называемый метод чисел Фибоначчи. Однако при этом в силу свойств чисел Фибоначчи количество итераций строго ограничено. Это удобно, если сразу задано количество возможных обращений к функции.

3. Метод золотого сечения.

Пусть задана функция . Тогда для того, чтобы найти определённое значение этой функции на заданном отрезке, отвечающее критерию поиска (пусть это будет минимум), рассматриваемый отрезок делится в пропорции золотого сечения в обоих направлениях, то есть выбираются две точки x₁ и x₂ такие, что:

где φ— пропорция золотого сечения.

Таким образом:

То есть точка x₁ делит отрезок [a,x₂] в отношении золотого сечения. Аналогично x₂ делит отрезок [x₁,b] в той же пропорции. Это свойство и используется для построения итеративного процесса.

Методы многомерной оптимизации включают в себя:

1. Методы нулевого порядка - методы, в которых при поиске экстремума используется информация только о самой функции и не используется информация о ее производных. Плюсом таких методов является возможность оптимизации функций, аналитическое представление которых неизвестно, т.е. эти функции определены только алгоритмически (метод покоординатного спуска, метод сопряженных направлений)

2. Методы первого порядка - при поиске решения используют не только информацию о самой функции, но и о её производных первого порядка. К таким методам относятся различные градиентные алгоритмы (метод наискорейшего спуска Коши, метод Флетчера-Ривса, Метод Флетчера-Пауэлла)

3. Методы второго порядка - при поиске решения используют инфор- мацию о самой функции и о её производных первого и второго порядка (метод Ньютона).

2. Метод Ньютона.

Пусть функция f дважды непрерывно дифференцируема и матрица Гессе f′′(x) – положительно определена для любых x∈Rⁿ . Здесь, как и прежде, будем искать точку X^*, в которой выполнено необходимое условие экстремума f′(X^*)=0. Итак, пусть имеется некоторая точка X^k. Рассмотрим разложение градиента в ряд Тейлора в окрестности этой точки:

,

где

.

Идея метода Ньютона заключается в замене функции f′(x) в окрестности точки x^k ее аппроксимацией f′(x^k)+‹f′′(x^k),x−x^k›.

Точку, в которой эта аппроксимация равна нулю, берут в качестве x^k+1:

x^k+1=x^k−[f′′(x^k)]⁻¹f′(x^k). (3)

Итак, задавая произвольную x⁰, запускают расчеты по формуле (3), проверяя на каждой итерации критерий остановки. Этот процесс является, очевидно, обобщением на случай функции многих переменных метода Ньютона-Рафсона, который, может расходиться, когда начальная точка далека от x^∗. Для того чтобы преодолеть эту проблему, алгоритм (3) модифицируют. Прежде, чем перейти к описанию этой модификации, отметим, что в силу положительной определенности f′′(x) направление p_k=−[f′′(x^k)]⁻¹f′(x^k) будет направлением спуска в точке x^k , так как

‹f ′(x^k),p_k›=‹f′(x^k),−[f′′(x^k)]⁻¹f′(x^k)›< 0. (4)

Таким образом, классический метод Ньютона можно рассматривать как процесс: , где .

В модифицированном же методе Ньютона предлагается искать α_k с помощью решения задачи одномерной минимизации:

Пример. Рассмотрим функцию , выберем x⁰=(1,1)^T и найдем точку минимума с помощью модифицированного метода Ньютона.

Имеем

 ; ; .

Отсюда

Поэтому окончательно

3. Метод ветвей и границ.

Рассмотрим задачу .

Допустим, что множество допустимых решений Q является конечным, тогда одним из алгоритмов решения этой задачи является полный перебор, когда наилучшее найденное решение, которое назовем рекордом, сравнивается с очередным допустимым решением. Понятно, что это очень неэффективный способ решения экстремальных задач. Так как приходится сравнивать друг с другом все решения, которых может оказаться слишком много. А в случае, когда задача непрерывна и множество допустимых решений континуально, не очень понятно как реализовать такую стратегию решения. Возникающие трудности можно попытаться обойти, если воспользоваться методом ветвей и границ (МВГ). Данный метод основан на переборе допустимых решений, в процессе которого рекорд сравнивается с подмножествами допустимых решений. Этот алгоритм осуществляет поиск оптимального решения посредством последовательного разбиения множества допустимых решений на подмножества меньшей мощности. Нижние оценки на значения целевой функции на этих подмножествах сравниваются с текущим рекордным значением целевой функции. Ясно, что подмножества решений, у которых нижние оценки больше текущего рекордного значения, не могут содержать оптимального решения и должны быть отброшены. В приводимом ниже описании метода ветвей и границ предположение о конечности множества Q не используется. Более важно свойство разложимости, которое описывается ниже, и предположение о конечности числа атомарных множеств.

Атомарным множеством назовем подмножество Q, на котором исходная задача легко решается точно или приближенно. Подмножество Q допустимых решений назовем разложимым, если оно представимо в виде объединения некоторого конечного набора атомарных множеств.

Обозначим через x(d) наилучшее решение задачи на атомарном множестве d, найденное с помощью некоторого алгоритма.

Функцией ветвления b(d) назовем функцию, определенную на разложимых подмножествах множества Q и ставящую в соответствие множеству d определенное его разбиение на несобственные разложимые подмножества.

Нижней границей назовем вещественную функцию H(d), определенную на разложимых подмножествах множества Q и такую, что

Функция H(d) невозрастающая, то есть  если

Суть метода ветвей и границ состоит в последовательном переборе вариантов, рассмотрении лишь тех из них, которые по определенным признакам оказываются перспективными, и отбрасывании бесперспективных вариантов. При использовании метода ветвей и границ область допустимых решений (ОДР) исходной задачи определенным способом разбивается на непересекающиеся подмножества, и решаются подзадачи, т.е. задачи на этих подмножествах с той же ЦФ и без учета условия целочисленности (как задачи ЛП). Если в результате получено оптимальное нецелочисленное решение, ОДР подзадачи снова разбивается на части и этот процесс продолжается до тех пор, пока не будет найдено оптимальное целочисленное решение исходной задачи.

Если в задаче на максимум при решении подзадач получаются оптимальные целочисленные решения, то запоминаются те из них, которым соответствуют возрастающие значения ЦФ. Если полученное «непрерывное» решение подзадачи оказывается не лучше сохраненного целочисленного решения, то такая подзадача исключается из списка задач. Название этого метода объясняется тем, что в процессе решения задача последовательно «ветвится», разбиваясь на более простые подзадачи.

Пример. Необходимо найти максимальное значение целевой функции

, при системе ограничений:

, (1)

, (2)

, (3)

, (4)

где x₁, x₂ - целые числа.

Границы области допустимых решений.

Строим прямую .

Максимум в точке C - пересечение прямых (1) и (2).

,

,

x₁ = 2,4, x₂ = 2,8

.

Разбиваем задачу 1 на 1.1 и 1.2. по х₁

Решим задачу 1.1

, (1)

, (2)

x₁≥3, (3)

x₁ ≥ 0, (4)

x₂ ≥ 0, (5)

Максимум в точке B - пересечение прямых (1) и (3).

,

x₁=3

, , x₂=2.2

.

Решим задачу 1.2

, (1)

, (2)

x₁≤2, (3)

x₁ ≥ 0, (4)

x₂ ≥ 0, (5)

Максимум в точке D - пересечение прямых (2) и (3).

,

x₁=2,

, , x₂ = 3

.

Разбиваем задачу 1 на 1.1 и 1.2. по х₂

Решим задачу 1.1

 (1)

, (2)

x₂≥3, (3)

x₁ ≥ 0, (4)

x₂ ≥ 0, (5)

Максимум в точке C - пересечение прямых (2) и (3).

,

x₂=3.

, , x₁ =2.

.

Текущий рекорд Z=18 ≥ 18.

Решим задачу 1.2

, (1)

, (2)

x₂≤2, (3)

x₁ ≥ 0, (4)

x₂ ≥ 0, (5)

Максимум в точке C - пересечение прямых (1) и (3).

5x₁+5x₂=26

x₂=2.

, , x₁=3,2

.

Текущий рекорд Z=18 ≥ 17.6.

F(X) = 18, x₁=2, x₂=3.

4. Метод наискорейшего градиентного спуска.

В методе наискорейшего спуска в качестве направления поиска выбирается вектор, направление которого противоположно направлению вектора градиента функции . Из математического анализа известно, что вектор  характеризует направление наиболее быстрого возрастания функции. Поэтому вектор  называется антиградиентом и является направлением наиболее быстрого ее убывания. Рекуррентное соотношение, с помощью которого реализуется метод наискорейшего спуска, имеет вид , k=0,1,…, где 𝜆_k>0 - величина шага. В зависимости от выбора величины шага можно получить различные варианты градиентного метода. Если в процессе оптимизации величина шага λ фиксирована, то метод носит название градиентного метода с дискретным шагом. Процесс оптимизации на первых итерациях можно значительно ускорить, если λ_k выбирать из условия .

Для определения λ_k используется любой метод одномерной оптимизации. В этом случае метод называется методом наискорейшего спуска. Как правило, в общем случае недостаточно одного шага для достижения минимума функции, процесс повторяют до тех пор, пока последующие вычисления позволяют улучшать результат.

Если пространство очень вытянуто по некоторым переменным, то образуется “овраг”. Поиск может замедлиться и идти зигзагами поперек дна “оврага”. Иногда решение невозможно получить за приемлемое время. 

Еще одним недостатком метода может быть критерий остановки

,

так как этому условию удовлетворяет и седловая точка, а не только оптимум.

Пример.

Найдем минимум функции f(x₁,x₂)=x₁²+2x₂²-2x₁x₂-x₁ методом наискорейшего спуска, начиная из точки (-2;2) с точностью ε=1.

Итерация №1.

.

.

f’(X₂)=0: 1170λ₁-225=0.

λ₁ = 0,1923.

Итерация №2.

5.

.

f’(X₃)=0: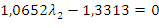

λ₂ = 1,2499.

Итерация №3.

.

Минимум целевой функции находится в точке

 и равен f(X₂) = 0,365.

 

 

Заключение.

Трудоемкость решения задачи оптимизации зависит от числа ее переменных, вида целевой функции, а также вида и числа ограничений. Часто методы, разработанные для решения того или иного типа задач, оказываются полезными для решения более сложных задач. Так, например, алгоритмы одномерной оптимизации широко применяются при решении многомерных задач; многие алгоритмы условной оптимизации используют методы безусловной оптимизации или являются их модификацией; методы решения задачи линейного программирования используются при решении задач нелинейного программирования и т. д.

Среди методов минимизации можно условно выделить конечношаговые и бесконечношаговые методы. Конечношаговыми, или конечными, называются методы, гарантирующие отыскание решения задачи за конечное число шагов. Конечношаговые методы удается построить лишь для некоторых специальных типов задач оптимизации, например, задач линейного и квадратичного программирования. Для бесконечношаговых методов достижение решения гарантируется лишь в пределе.

Список литературы.

1. Алексеева Е.В. Численные методы оптимизации: учебное пособие / Е.В.Алексеева, О.А.Кутненко, А.В.Плясунов.- Новосиб.: ун-т. Новосибирск, 2008.

2. Васильев Ф.П. Методы оптимизации: учебник / Ф.П.Васильев.- М.: «Факториал Пресс», 2002.

3. Измаилов А.Ф. Численные методы оптимизации: учебное пособие / А.Ф.Измаилов, М.В.Солодов.- М.: ФИЗМАТЛИТ, 2005

4. Мастяева И.Н. Методы оптимизации: учебное пособие / О.Н. Семенихина, И.Н.Мастяева.- М.: МЭСИ, 2003.

5. Рейзлин В.И. Численные методы оптимизации: учебное пособие / В.И. Рейзлин. – Томск: Изд-во Томского политехнического университета, 2011.

6. Трифонов А.Г. Постановка задачи оптимизации и численные методы ее решения [электронный ресурс] / А.Г. Трифонов. // SoftLine Со. Свободный режим доступа: http://matlab. exponenta.ru/optimiz/book_2/index.php