структуры данных и алгоритмы

Министерство образования и науки Российской Федерации

НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

КАФЕДРА ПРИКЛАДНОЙ МАТЕМАТИКИ

Курсовая работа

по практикуму на ЭВМ: структуры данных и алгоритмы

Факультет:  прикладной математики и информатики

Группа: ПМ-01

Студент: Гайворонских А. С

Преподаватель: Тракимус Ю. В

Новосибирск

2011

1.      Условие задачи

Дан граф G. Построить транзитивное замыкание графа G G’. Вершины i и j соединены ребром в транзитивном замыкании G’ тогда и только тогда, когда существует путь между вершинами i и j в исходном графе G.

2.      Анализ задачи

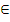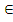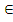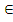Транзитивное отношение – если для всех x, y, z  A из того, что (x,y) P и (y,z) P, следует, что (x,z) P.

Графические особенности диаграммы: для любых двух дуг, таких, что одна направлена от а к b, а другая от b к с, существует дуга, соединяющая а и с в направлении от а к с.

Характеристики графа:

- ориентированный – поскольку это позволит решить задачу в более широком смысле (т.к неориентированный граф можно рассматривать, как частный случай ориентированного)

- размеченный – каждой вершине необходимо поставить в соответствие какое-либо имя, которое бы отличало ее от других вершин.

- невзвешенный – в задаче ничего не сказано о весе ребер, поэтому для однозначности будем считать все ребра равными, с длиной равной 1.

- несвязный – это позволит решить задачу в более широком смысле.

- простой – наличие кратных ребер и петель не влияет на транзитивность, т.к всегда рассматриваются минимум 3 различные вершины: x, y и z.

Дано:

ГрафG = (V, E)

Результат:

Граф  G’ = (V, E’) – транзитивное замыкание графа G

Решение:

W[N][N] – матрица достижимости

graph[N][N] – матрица смежности

Строится матрица достижимости. Если из одной вершины в другую существует путь, то в матрицу достижимости заносится 1, в противном случае 0.

W[ i ][ j ] = graph [ i ][ j ]

Повторять

W[ i ][ j ] = W[ i ][ j ] или (W[ i ][ k ] и W[ k ][ j ])

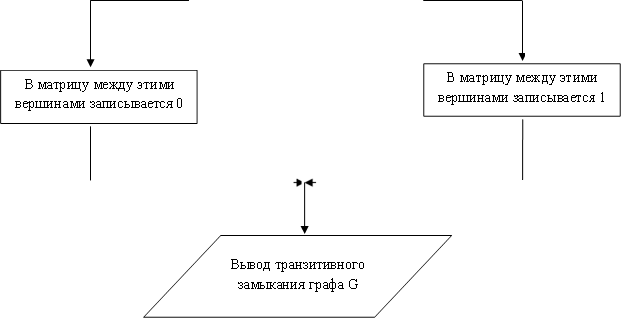
Вывод транзитивного замыкания графа G по полученной матрице достижимости.

Таким образом, можно выделить две основные подзадачи:

1. Построение матрицы достижимости. Для этого  можно воспользоваться алгоритмом Уоршелла (представлен выше);

2. Вывод транзитивного замыкания графа G.

3.   Структуры данных, используемые для представления исходных данных и результатов задачи

Входные данные. Внешнее представление

Набор символов (имена вершин), попарно записанных в столбец – перечисление ребер графа.

Входные данные. Внутреннее представление

При применении алгоритма Уоршелла строится матрица достижимости, и её заполнение существенно облегчается, т.к изначально была использована матрица смежности. Названия вершин помещаются в отдельный список, обеспечивается связь между матрицей смежности и матрицей достижимости по номерам столбцов и строк.

char name[N][255]-список имен вершин

int graph[N][N] - матрица смежности

n – количество вершин (вычисляется при вводе)

Выходные данные. Внешнее представление

Набор символов (имена вершин), попарно записанных в столбец – перечисление ребер транзитивного замыкания графа G.

Выходные данные. Внутреннее представление

Матрица достижимости, составленная из нулей и единиц: 1 если существует путь из одной вершины в другую в исходном графе, 0 в противном случае.

4.      Укрупненный алгоритм решения задачи

              -                                                                           +

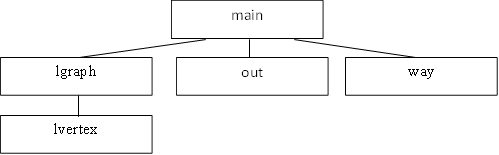
5.      Структура программы

Главная функция main. Прототип: int main()

Назначение: передача управления между остальными функциями, вывод конечного результата работы программы.

Функция lvertex. Прототип: int lvertex (FILE *F)

Назначение: поиск номера вершины, являющегося одним из концов вводимого ребра, ввод названия вершины в список названий вершин.

*F – указатель на файл, из которого происходит чтение.

Процедура lgraph. Прототип void lgraph()

Назначение: ввод системы ребер.

Процедура out. Прототип: void out(int G[N][N], int n)

n - Количество вершин

G[N][N] – матрица смежности

Назначение: построение матрицы достижимости.

Процедура way. Прототип void way(int G[N][N], int W[N][N], int n)

n - Количество вершин

G[N][N] – матрица смежности

W[N][N] – матрица достижимости

Назначение: вывод транзтивного замыкания графа G по матрице достижимости.

 

6.      Текст программы на языке Си

#include

#include

const int N = 1024;

char name[N][255];

int graph[N][N], W[N][N];

int n = 0;

int lvertex(FILE *F){

       char namevertex[255];

       int number,i,sign,fl = 1;

       fscanf( F, "%s", &namevertex );

       for (i = 0; i < n; i++){

             sign = strcmp( namevertex, name[ i ]);

             if( sign == 0 )

                    number = i;

             fl = fl * sign;}

       if (fl != 0){

             strcpy(name[ n ], namevertex);

             number = n;

             n = n + 1;}

       return number;}

void lgraph(){

       FILE *F;

       int k,l;

       F = fopen( "graph.txt", "r" );

       while (!feof( F )){

             k = lvertex(F);

             l = lvertex(F);

             graph[ k ][ l ] = 1;}

       fclose( F );}

void way(int G[N][N], int W[N][N], int n){

       int i, j, k;

       for (i = 0; i < n; i++)

             for (j = 0; j < n; j++)

                    W[ i ][ j ] = G[ i ][ j ];

       for (k = 0; k < n; k++)

             for (i = 0; i < n; i++)

                    for (j = 0; j < n; j++)

                           W[ i ][ j ] = W[ i ][ j ] || (W[ i ][ k ] && W[ k ][ j ]);}

void out(int G[N][N], int n){

       FILE *F;

       int i, j;

       F = fopen("output.txt", "w");

       for ( i = 0; i < n; i++){

             for (j = 0; j < n; j++)

                    if ((i != j) && (G[ i ][ j ] == 1))                        

                           fprintf(F, "%s - %s  ", name[ i ], name[ j ]);}

       fprintf(F, " ");}

void main(){

       loadgraph();

       way(graph, W, n);

       out(W, n);}

7.      Набор тестов

Тест 1.

Назначение: транзитивного замыкания нет

Входные данные:

1 - 2

1 - 3

Результат:

1 - 2

1 - 3

 

Тест 2.

Назначение: циклический граф с малым количеством ребер

Входные данные:

1 - 2

2 - 3

3 - 4

4 - 5

5 - 1

Выходные данные:

1 - 2   1 - 3   1 - 4   1 - 5

2 - 1   2 - 3   2 - 4   2 - 5

3 - 1   3 - 2   3 - 4   3 - 5

4 - 1   4 - 2   4 - 3   4 - 5

5 - 1   5 - 2   5 - 3   5 – 4

Тест 3.

Назначение: граф с различными направлениями ребер

Входные данные:

1 – 5   4 - 6

2 – 1   5 - 8

2 – 3   6 - 7

3 – 5   8 - 7

3 – 4   8 - 9

3 – 9

Выходные данные:

1 - 5   1 - 9   1 - 8   1 - 7

5 - 9   5 - 8   5 - 7

2 - 1   2 - 5   2 - 3   2 - 4   2 - 9   2 - 6   2 - 8   2 - 7

3 - 5   3 - 4   3 - 9   3 - 6   3 - 8   3 - 7

4 - 6   4 - 7

6 - 7

8 - 9   8 - 7

8.      Результаты работы программы

№	Входные данные	Результат выполнения
1
2
3
4
5	1 2 2 3 3 4 4 1 1 5 5 3 5 2 5 4	2
6	1 2          B 15 2 3          C E 3 4          C D 4 5          D 7 5 6          E F 6 7          7 I 7 8          F G 8 9          G H 9 10         I H 10 11       G 14 11 12       H 13 12 13       H J 13 14       J 13 14 F         I J F 15         8 K 15 16       K J 16 1         J 12 3 A          K W A C         W 11 C B         W 10