Вариант № 7
Исходные данные для выполнения курсовой работы
В результате выборочного обследования 10% рабочих авиаремонтного завода (по состоянию на 01 января текущего года) получены следующие данные:
| №№ п/п | Разряд | Производственный стаж, полных лет | Заработная плата, у.е. |
| 1 | 2 | 3 | 4 |
| Цех № 1 | |||
| 1 | 4 | 5 | 539 |
| 2 | 1 | 1 | 487 |
| 3 | 4 | 7 | 554 |
| 4 | 2 | 2 | 507 |
| 5 | 1 | 1 | 490 |
| 6 | 2 | 5 | 519 |
| 7 | 3 | 8 | 536 |
| 8 | 5 | 10 | 574 |
| 9 | 2 | 0 | 481 |
| 10 | 3 | 7 | 533 |
| 11 | 2 | 2 | 515 |
| 12 | 2 | 3 | 524 |
| 13 | 5 | 5 | 553 |
| 14 | 1 | 1 | 479 |
| 15 | 3 | 4 | 509 |
| 16 | 3 | 8 | 552 |
| 17 | 2 | 3 | 526 |
| 18 | 2 | 1 | 495 |
| 19 | 1 | 0 | 492 |
| 20 | 4 | 6 | 562 |
| 21 | 2 | 5 | 516 |
| 22 | 1 | 0 | 483 |
| 23 | 4 | 8 | 531 |
| 24 | 4 | 12 | 548 |
| 25 | 2 | 4 | 521 |
| 26 | 3 | 7 | 529 |
| 27 | 3 | 6 | 520 |
| 28 | 2 | 1 | 475 |
| 29 | 3 | 8 | 525 |
| 30 | 1 | 0 | 472 |
| 31 | 4 | 3 | 553 |
| 32 | 2 | 4 | 518 |
| 33 | 1 | 0 | 485 |
| 34 | 2 | 3 | 508 |
| 35 | 3 | 8 | 507 |
| 36 | 5 | 17 | 578 |
| 37 | 2 | 1 | 505 |
| 38 | 6 | 23 | 600 |
| 39 | 3 | 4 | 528 |
| 40 | 3 | 11 | 538 |
| Цех № 2 | |||
| 1 | 3 | 5 | 536 |
| 2 | 2 | 1 | 501 |
| 3 | 3 | 3 | 517 |
| 4 | 4 | 15 | 571 |
| 5 | 2 | 1 | 492 |
| 6 | 4 | 19 | 562 |
| 7 | 1 | 0 | 480 |
| 8 | 3 | 5 | 541 |
| 9 | 3 | 7 | 535 |
| 10 | 2 | 1 | 502 |
| 11 | 3 | 3 | 528 |
| 12 | 4 | 12 | 565 |
| 13 | 4 | 2 | 525 |
| 14 | 5 | 6 | 536 |
| 15 | 5 | 8 | 574 |
| 16 | 3 | 3 | 523 |
| 17 | 6 | 29 | 571 |
| 18 | 2 | 3 | 498 |
| 19 | 4 | 13 | 537 |
| 20 | 3 | 8 | 530 |
| 21 | 1 | 1 | 494 |
| 22 | 2 | 0 | 468 |
| 23 | 4 | 3 | 513 |
| 24 | 3 | 9 | 547 |
| 25 | 6 | 9 | 594 |
| 26 | 5 | 12 | 588 |
| 27 | 1 | 2 | 504 |
| 28 | 3 | 6 | 523 |
| 29 | 1 | 0 | 460 |
| 30 | 4 | 14 | 536 |
| 31 | 2 | 4 | 517 |
| 32 | 3 | 5 | 535 |
| 33 | 3 | 0 | 492 |
| 34 | 4 | 15 | 553 |
| 35 | 5 | 8 | 573 |
| 36 | 2 | 1 | 486 |
| 37 | 4 | 2 | 543 |
| 38 | 3 | 4 | 522 |
| 39 | 3 | 7 | 534 |
| 40 | 4 | 10 | 558 |
| 41 | 2 | 4 | 506 |
| 42 | 2 | 4 | 512 |
| 43 | 3 | 11 | 552 |
| 44 | 4 | 5 | 527 |
| 45 | 4 | 7 | 547 |
| 46 | 5 | 15 | 595 |
| 47 | 3 | 4 | 514 |
| 48 | 3 | 8 | 555 |
| 49 | 3 | 9 | 524 |
| 50 | 2 | 4 | 505 |
| 51 | 4 | 11 | 559 |
| 52 | 1 | 1 | 491 |
| 53 | 3 | 9 | 534 |
| 54 | 4 | 10 | 552 |
| 55 | 3 | 2 | 526 |
| 56 | 5 | 21 | 597 |
| 57 | 3 | 8 | 521 |
| 58 | 2 | 0 | 483 |
| 59 | 5 | 13 | 575 |
| 60 | 2 | 2 | 508 |
1. Построить ряд распределения рабочих каждого цеха и завода в целом по размеру заработной платы, выделив 7 групп с равными интервалами. Определить в целом по заводу моду и медиану заработной платы рабочих.
2. Рассчитать средний тарифный разряд, средний производственный стаж рабочих завода, коэффициент вариации этих показателей. Сделать выводы.
3. Рассчитать среднюю заработную плату и дисперсию заработной платы рабочих завода обычным способом и способом условных моментов.
4. С вероятностью 0,954 определить ошибку выборки средней заработной платы рабочих цеха № 1 и для доли рабочих цеха № 1, имеющих заработную плату менее 500 у.е. Указать пределы возможных значений этих показателей в генеральной совокупности. Какая вероятность того, что доля рабочих, имеющих заработную плату до 500 у.е., в генеральной совокупности не превысит 30%?
5. Определить количественную взаимосвязь между признаками:
5.1. С помощью графического метода определить форму связи между производственным стажем и заработной платой рабочих цеха № 1 с № 21 по № 40 включительно (п=20).
5.2. Вычислить параметры уравнения регрессии, характеризующие зависимость между производственным стажем и заработной платой рабочих. Построить на графике теоретическую и эмпирическую линии регрессии. Объяснить смысл полученных параметров уравнения.
5.3.Определить степень тесноты связи между рассматриваемыми признаками
Решение
1)Построим ряд распределения рабочих каждого цеха и завода в целом по размеру заработной платы, выделив 7 групп с равными интервалами. Определим в целом по заводу моду и медиану заработной платы рабочих
1.1) Итак, для того, чтобы произвести группировку рабочих по размеру заработной платы, (факторный группировочный признак), выделив 7 групп с равными интервалами, нужно рассчитать ширину равного интервала по формуле:
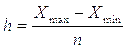 , (1.1)
, (1.1)
где 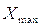 ,
, 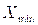 – максимальное и минимальное значение признака,
– максимальное и минимальное значение признака,
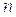 – число групп.
– число групп.
Округления произведем в большую сторону для облегчения дальнейших расчетов.
Для цеха №1:
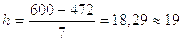 у.е
у.е
Для цеха №2:
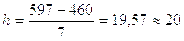 у.е
у.е
Для завода в целом:
 у.е
у.е
Произведем группировку рабочих цеха № 1 оформим в таблицу 1.., рабочих цеха 2 в таблицу 1.2, а завода в целом в таблицу 1.3.
Таблица 1.1
Ряд распределения рабочих цеха № 1 по размеру заработной платы
| Группы рабочих цеха № 1 по размеру заработной платы, у.е. (Варианты, х) | Число рабочих (частоты) f |
| 472-491 | 8 |
| 491-510 | 7 |
| 510-529 | 11 |
| 529-548 | 6 |
| 548-567 | 5 |
| 567-586 | 2 |
| 586 и более | 1 |
| Всего | 40 |
Таблица 1.2
Ряд распределения рабочих цеха № 2 по размеру заработной платы
| Группы рабочих цеха № 2 по размеру заработной платы, у.е. (Варианты, х) | Число рабочих (частоты) f |
| 460-480 | 3 |
| 480-500 | 7 |
| 500-520 | 11 |
| 520-540 | 18 |
| 540-560 | 10 |
| 560-580 | 7 |
| 580 и более | 4 |
| Всего | 60 |
Таблица 1.3
Ряд распределения рабочих завода по размеру заработной платы
| Группы рабочих завода по размеру заработной платы, у.е. | Число рабочих f | Накопленная частота | Середина интервала х | xf |
|
|
| А | 1 | 2 | 3 | 4 | 5 | |
| 460-480 | 6 | 6 | 470 | 2820 | -56,6 | 19221,36 |
| 480-500 | 14 | 20 | 490 | 6860 | -36,6 | 18753,84 |
| 500-520 | 21 | 41 | 510 | 10710 | -16,6 | 5786,76 |
| 520-540 | 29 | 70 | 530 | 15370 | 3,4 | 335,24 |
| 540-560 | 15 | 85 | 550 | 8250 | 23,4 | 8213,4 |
| 560-580 | 10 | 95 | 570 | 5700 | 43,4 | 18835,6 |
| 580-600 | 5 | 100 | 590 | 2950 | 63,4 | 20097,8 |
| Всего | 100 | - | x | 52660 | х | 91244 |
1.3)Рассчитываем моду (по результатам группировки рабочих всего завода) по формуле:
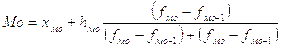 , (1.1)
, (1.1)
где 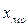 -нижняя граница модального интервала (модальным называется интервал, имеющий наибольшую частоту);
-нижняя граница модального интервала (модальным называется интервал, имеющий наибольшую частоту);
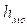 - величина модального интервала;
- величина модального интервала;
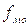 - частота модального интервала;
- частота модального интервала;
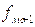 - частота интервала, предшествующего модальному;
- частота интервала, предшествующего модальному;
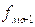 - частота интервала, следующего за модальным.
- частота интервала, следующего за модальным.
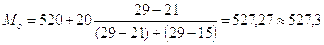 у.е.
у.е.
1.4)Рассчитываем медиану по формуле:
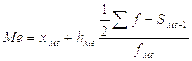 , (1.2)
, (1.2)
где: 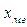 -нижняя граница медианного интервала (медианным называется первый интервал, накопленная частота которого превышает половину общей суммы частот);
-нижняя граница медианного интервала (медианным называется первый интервал, накопленная частота которого превышает половину общей суммы частот);
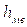 -величина медианного интервала;
-величина медианного интервала;
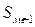 -накопленная интервала, предшествующего медианному;
-накопленная интервала, предшествующего медианному;
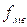 - частота медианного интервала.
- частота медианного интервала.
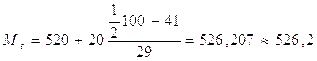 у.е.
у.е.
Выводы: в результате группировки рабочих по цеху № 1 было сгруппировано 7 групп. Согласно данному распределению получили вариационный интервальный ряд, из которого следует, что 11 рабочих имеют заработную плату от 510 у.е. до 529 у.е.
В результате группировки рабочих по цеху № 2 было сгруппировано 7 групп. Согласно данному распределению получили вариационный интервальный ряд, из которого следует, что 18 рабочих имеют заработную плату от 520 у.е. до 540 у.е.
В результате группировки рабочих по заводу в целом было сгруппировано 7 групп. Согласно данному распределению получили вариационный интервальный ряд, из которого следует, что 29 рабочих имеют заработную плату от 520 у.е. до 540 у.е.
Чаще всего среди рабочих завода встречаются работники с заработной платой 527,3 у.е.
Половина всех работников имеют заработную плату больше чем 526,2 у.е., а другая половина рабочих - меньше, чем 526,2 у.е.
2. Рассчитываем средний тарифный разряд, средний производственный стаж рабочих завода, коэффициент вариации этих показателей.
2.1) Для расчета среднего тарифного разряда и упрощения расчетов произведем предварительно группировку всех рабочих завода. В результате группировки получим следующий ряд распределения рабочих завода по тарифному разряду.
Таблица 2.1
Группировка рабочих завода по тарифному разряду
| Группы рабочих завода по тарифному разряду. | Число рабочих f | xf |
|
|
| А | 1 | 2 | 3 | 4 |
| 1 | 12 | 12 | -2 | 48 |
| 2 | 25 | 50 | -1 | 25 |
| 3 | 30 | 90 | 0 | 0 |
| 4 | 20 | 80 | 1 | 20 |
| 5 | 10 | 50 | 2 | 40 |
| 6 | 3 | 18 | 3 | 27 |
| Всего | 100 | 300 | х | 160 |
2.2) Рассчитываем средний тарифный разряд рабочих завода по формуле средней арифметической взвешенной (так как мы сгруппировали данные):
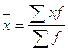
(2.1)
где 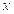 - индивидуальные значения осредняемого признака;
- индивидуальные значения осредняемого признака;
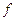 - это частота повторения признака.
- это частота повторения признака.
Все необходимые промежуточные расчеты указаны в таблице 2.1. Тогда:
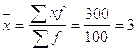
2.3) Определяем дисперсию по формуле:
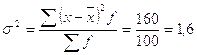 (2.2)
(2.2)
2.4)Определяем среднее квадратическое отклонение, которое представляет собой корень из дисперсии. Поэтому формула будет иметь вид:
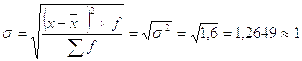 разряд (2.3)
разряд (2.3)
2.5)Определяем коэффициент вариации тарифного разряда по формуле:
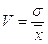 , (2.4)
, (2.4)
где: 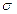 - среднее квадратическое отклонение
- среднее квадратическое отклонение
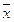 - среднее значение исследуемого признака
- среднее значение исследуемого признака
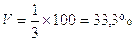
2.6) Для того, чтобы рассчитать средний производственный стаж рабочих завода сгруппируем рабочих по производственному стажу.
Сформируем группы рабочих завода по производственному стажу с неравными прогрессивно-возрастающими интервалами в арифметической прогрессии.
Величина интервалов, изменяющихся в арифметической прогрессии, определяется следующим образом:
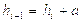
где а – константа, имеющая для прогрессивно-возрастающих интервалов
Группа № 1 - 0-3
Группа № 2 – 3-9
Группа № 3 – 9-18
Группа № 4 – 18 и более
2.7) Проведем группировку рабочих по производственному стажу и представим полученные дынные в виде статистического ряда распределения (таблица 2.2)
Таблица 2.2
Группировка рабочих завода по производственному стажу
| Группы рабочих завода по производственному стажу, лет | Число рабочих f | Середина интервала х | xf |
|
|
| А | 1 | 2 | 3 | 4 | 5 |
| 0-3 | 38 | 1,5 | 57 | -4,5 | 769,5 |
| 3-9 | 42 | 6,0 | 252 | 0 | 0 |
| 9-18 | 16 | 13,5 | 216 | 7,5 | 900 |
| 18 и более | 4 | 22,5 | 90 | 16,5 | 1089 |
| Всего | 100 | х | 615 | х | 2758,5 |
2.8) Рассчитываем средний производственный стаж рабочих завода по формуле 2.1.
Все необходимые промежуточные расчеты для расчета дисперсии и коэффициента вариации указаны в таблице 2.2. Тогда:
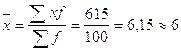 полных лет
полных лет
2.9) Определяем дисперсию по формуле 2.2:
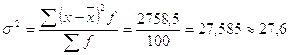
2.10)Определяем среднее квадратическое отклонение по формуле 2.3:
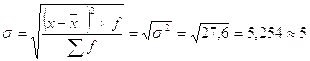 полных лет
полных лет
2.11)Определяем коэффициент вариации тарифного разряда по формуле 2.4:
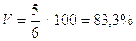
Выводы: средний тарифный разряд рабочих по заводу в целом составляет 3 разряд, а средний производственный стаж рабочих по заводу в целом составляет 6 полных лет.
Анализ полученных значений показателей 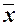 и σ говорит о том, что отклонение от среднего значения тарифного разряда рабочих в ту или иную сторону составляет в среднем 1 разряд (или 33,3%), наиболее характерные значения тарифного разряда рабочих находятся в пределах от 2-го разряда до 4-го разряда (диапазон
и σ говорит о том, что отклонение от среднего значения тарифного разряда рабочих в ту или иную сторону составляет в среднем 1 разряд (или 33,3%), наиболее характерные значения тарифного разряда рабочих находятся в пределах от 2-го разряда до 4-го разряда (диапазон 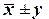 ).
).
А отклонение от среднего значения производственного стажа рабочих в ту или иную сторону составляет в среднем 5 полных лет (или 83,3%), наиболее характерные значения производственного стажа рабочих находятся в пределах от 1-го года до 11 лет (диапазон 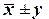 ).
).
Значение коэффициента вариации тарифного разряда V=33,3% не превышает 33,3%, следовательно, вариация тарифного разряда в исследуемой совокупности рабочих завода незначительна и совокупность по данному признаку качественно однородна.
А значение коэффициента вариации производственного стажа рабочих, в отличие от коэффициента вариации тарифного разряда рабочих, превышает 33,3% (V=83,3%), следовательно, вариация рабочих по производственного стажу в исследуемой совокупности рабочих завода значительна и совокупность по данному признаку качественно неоднородна.
3) Рассчитываем среднюю заработную плату и дисперсию заработной платы рабочих завода обычным способом и способом условных моментов.
3.1) На основании составленной таблицы 3.1. рассчитываем среднюю заработную плату рабочих завода обычным способом по формуле 2.2.
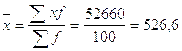 у.е.
у.е.
3.2) Определяем дисперсию (обычным способом) по формуле 2.2:
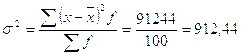
3.3) Рассчитываем среднюю заработную плату рабочих завода способом условных моментов
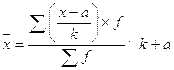 (3.1)
(3.1)
где: а - размер варианта при наибольшей частоте;
k - размер интервала при наибольшей частоте
Результаты расчета дисперсии рабочих поместим в таблицу 3.1.
а =530 k = 20
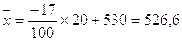 у.е.
у.е.
3.4)Рассчитываем дисперсию (вторым способом) по формуле [10; с.134]:
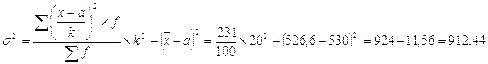 (3.2)
(3.2)
Таблица 3.1
Вспомогательная таблица для расчета средней и дисперсии методом моментов
| Группы рабочих завода по размеру заработной платы, у.е. | Число рабочих f | Середина интервала х | х-а |
|
|
|
|
| А | 1 | 3 | 4 | 5 | 6 | 7 | 8 |
| 460-480 | 6 | 470 | -60 | -3 | -18 | 9 | 54 |
| 480-500 | 14 | 490 | -40 | -2 | -28 | 4 | 56 |
| 500-520 | 21 | 510 | -20 | -1 | -21 | 1 | 21 |
| 520-540 | 29 | 530 | 0 | 0 | 0 | 0 | 0 |
| 540-560 | 15 | 550 | 20 | 1 | 15 | 1 | 15 |
| 560-580 | 10 | 570 | 40 | 2 | 20 | 4 | 40 |
| 580-600 | 5 | 590 | 60 | 3 | 15 | 9 | 45 |
| Всего | 100 | x | x | x | -17 | x | 231 |
3.5)Определяем среднее квадратическое отклонение по формуле 2.3:
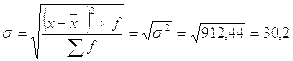 у.е.
у.е.
Выводы: средняя заработная плата рабочих по заводу в целом составляет 526,6 у.е.
Анализ полученных значений показателей 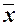 и σ говорит о том, что отклонение от среднего значения заработной платы рабочих завода в ту или иную сторону составляет в среднем 30,2 у.е. Наиболее характерные значения размера заработной платы рабочих находятся в пределах от 496,4 у.е. до 556,8 у.е. (диапазон
и σ говорит о том, что отклонение от среднего значения заработной платы рабочих завода в ту или иную сторону составляет в среднем 30,2 у.е. Наиболее характерные значения размера заработной платы рабочих находятся в пределах от 496,4 у.е. до 556,8 у.е. (диапазон 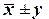 ).
).
4) С вероятностью 0,954 определим ошибку выборки средней заработной платы рабочих цеха № 1. Укажем пределы возможных значений этих показателей в генеральной совокупности.
На основании данных таблицы 1.1 и для удобства и простоты дальнейших расчетов составим вспомогательную таблицу 4.1.
Таблица 4.1
Вспомогательная таблица
| Группы рабочих цеха № 1 по размеру заработной платы, у.е. (Варианты, х) | Число рабочих (частоты) f | Середина интервала, х | xf |
|
|
| 472-491 | 8 | 481,5 | 3852 | -39,7 | 12608,7 |
| 491-510 | 7 | 500,5 | 3503,5 | -20,7 | 2999,43 |
| 510-529 | 11 | 519,5 | 5714,5 | -1,7 | 31,79 |
| 529-548 | 6 | 538,5 | 3231 | 17,3 | 1795,74 |
| 548-567 | 5 | 557,5 | 2787,5 | 36,3 | 6588,45 |
| 567-586 | 2 | 576,5 | 1153 | 55,3 | 6116,18 |
| 586 и более | 1 | 605,0 | 605 | 83,8 | 7022,44 |
| Всего | 40 | х | 20846,5 | х | 37162,8 |
4.1) Рассчитываем среднюю заработную плату рабочих цеха № 1 по формуле средней арифметической взвешенной, используя промежуточные расчеты таблицы 4.1:
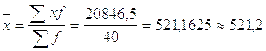 у.е.
у.е.
4.2) Так как была произведена 10% выборка рабочих цеха № 1, то именно эти 40 рабочих создают выборочную совокупность. Это означает вся численность совокупности равняется N=40/0,1=400 рабочих.
4.3)Определяем дисперсию по формуле 2.2:
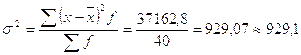 у.е.
у.е.
4.4) Рассчитаем среднюю ошибку выборки для средней заработной платы рабочих цеха № 1:
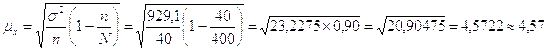 у.е. (4.1)
у.е. (4.1)
4.5)Рассчитываем граничную ошибку выборки. Коэффициент доверия t при заданной вероятности 0,954 равняется :
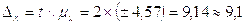 у.е. (4.2)
у.е. (4.2)
Таким образом, генеральная средняя составляет:
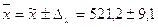 (4.3)
(4.3)
А это означает, что:
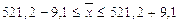
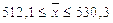
Выводы: с вероятностью 0,954 можно утверждать, что средняя заработная плата рабочих цеха № 1 находится в пределах от 512,1 у.е. до 5230,3 у.е.
4.6) С вероятностью 0,954 определим ошибку выборки для доли рабочих цеха № 1, имеющих заработную плату менее 500 у.е. Укажем пределы возможных значений этих показателей в генеральной совокупности.
Итак, из общего числа работников цеха № 1, отобрали рабочих, у которых заработная плата менее 500у.е. Их число составляет 10 (по таблице 1.1.) Это означает, что доля таких рабочих в выборочной совокупности 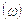 составляет:
составляет: 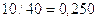 или 25,0%.
или 25,0%.
Тогда средняя ошибка выборки для доли 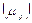 будет составлять:
будет составлять:
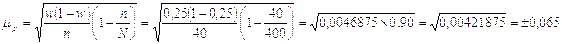 или
или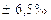 (4.4)
(4.4)
4.7)Коэффициент доверия t при заданной вероятности 0,954 равняется 2. Тогда граничная ошибка выборки при вероятности 0,954 для доли
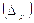 составляет:
составляет:
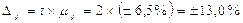 (4.5)
(4.5)
Итак, доля рабочих цеха № 1, у которых заработная плата менее 500 у.е. во всей генеральной совокупности составляет:
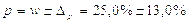 (4.6)
(4.6)
а это означает, что:
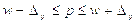
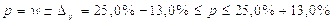 или
или 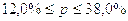
Выводы: С вероятностью 0,954 можно утверждать, что доля рабочих цеха № 1, у которых заработная плата менее 500 у.е. в генеральной совокупности находится в пределах от 12,0% до 38,0%.
4.7) Определим какая вероятность того, что доля рабочих, имеющих заработную плату до 500 у.е., в генеральной совокупности не превысит 30%.
Итак, допустим, что доля рабочих, имеющих заработную плату до 500у.е. в генеральной совокупности не превысит 30%
Граничная ошибка выборки для доли составляет: 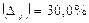
А средняя ошибка для доли составляет 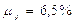
Определим коэффициент доверия t :
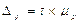 Тогда:
Тогда: 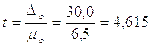
По таблице Лапласа определим, что вероятность при коэффициенте t=4,615 составляет 0,999965
Выводы: с вероятностью 0,999965 доля рабочих, имеющих заработную плату до 500 у.е., в генеральной совокупности не превысит 30%.
5. Определим количественную взаимосвязь между признаками:
5.1. С помощью графического метода определим форму связи между производственным стажем и заработной платой рабочих цеха № 1 с № 21 по № 40 включительно (п=20).
Сущность графического метода заключается в построении поля корреляции, которое представляет собой точечный график, для построения которого в прямоугольной системе координат по оси абсцисс откладывают значения факториального признака, а по оси ординат - результативного. По тому как располагаются точки, судят о наличии и форме связи.
В данном случае производственный стаж будет факториальным признаком, а заработная плата - результативным, т.к. она зависит от производственного стажа (выслуги).
Изобразим эту взаимосвязь на рисунке 5.1.
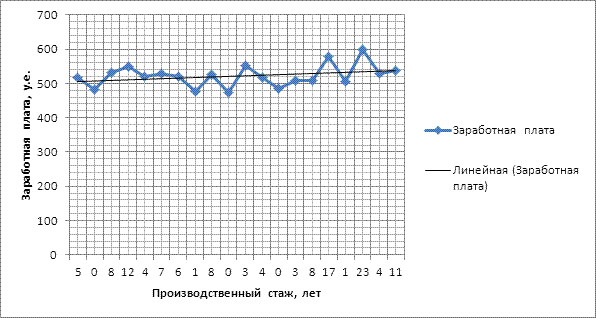
Рис.5.1. Корреляционное поле и теоретическая линия регрессии зависимости производственного стажа рабочих цеха № 1 от заработной платы
По графику 5.1 можно определить, что связь стохастическая, т.к. каждому значению факториального признака (х), соответствует некоторое множество значений результативного признака (у).
Корреляционная связь между признаками проявляется в том, что при изменении признака (х) на единицу изменяется средняя величина признака (у). В данном случае связь линейная прямая, т.к. с возрастанием производственного стажа (х) увеличивается заработная плата (у).
5.2. Вычислим параметры уравнения регрессии, характеризующие зависимость между производственным стажем и заработной платой рабочих.
Из рисунка 5.1. видно, что связь между производственным стажем и заработной платой рабочих прямая, значит она выражается уравнением прямой: 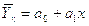 , (5.1)
, (5.1)
где 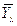 - выровненные (теоретические) значения результативного признака (ставка);
- выровненные (теоретические) значения результативного признака (ставка);
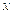 - факторный признак (срок выдачи кредита);
- факторный признак (срок выдачи кредита);
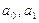 - параметры уравнения регрессии.
- параметры уравнения регрессии.
Параметр а0 - показывает уровень заработной платы на который влияют другие факторы, которые в данном случае не рассматриваются.
Параметр а1 (коэффициент регрессии) - показывает на сколько в среднем изменяется результативный признак (у) при увеличении факториального признака (х) на единицу.
Параметры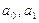 находят из системы нормальных уравнений
находят из системы нормальных уравнений
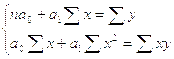
Тогда расчет коэффициентов 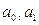 будет иметь вид:
будет иметь вид:

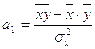 (5.2)
(5.2)
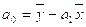 (5.3)
(5.3)
где: 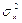 - выборочная дисперсия признака х;
- выборочная дисперсия признака х;
Составим вспомогательную таблицу 5.1, в которой укажем все промежуточные расчеты.
Таблица 5.1.
Рабочая таблица расчета промежуточных данных для определения линейного коэффициента корреляции и значений уравнения регрессии
| № пп | Производственный стаж, полных лет. (х) | Заработная плата, у.е (у) |
|
|
| Выровненный ряд
|
| 1 | 5 | 516 | 2580 | 25 | 266256 | 516 |
| 2 | 0 | 483 | 0 | 0 | 233289 | 492 |
| 3 | 8 | 531 | 4248 | 64 | 281961 | 530 |
| 4 | 12 | 548 | 6576 | 144 | 300304 | 549 |
| 5 | 4 | 521 | 2084 | 16 | 271441 | 511 |
| 6 | 7 | 529 | 3703 | 49 | 279841 | 526 |
| 7 | 6 | 520 | 3120 | 36 | 270400 | 521 |
| 8 | 1 | 475 | 475 | 1 | 225625 | 497 |
| 9 | 8 | 525 | 4200 | 64 | 275625 | 530 |
| 10 | 0 | 472 | 0 | 0 | 222784 | 492 |
| 11 | 3 | 553 | 1659 | 9 | 305809 | 506 |
| 12 | 4 | 518 | 2072 | 16 | 268324 | 511 |
| 13 | 0 | 485 | 0 | 0 | 235225 | 492 |
| 14 | 3 | 508 | 1524 | 9 | 258064 | 506 |
| 15 | 8 | 507 | 4056 | 64 | 257049 | 530 |
| 16 | 17 | 578 | 9826 | 289 | 334084 | 573 |
| 17 | 1 | 505 | 505 | 1 | 255025 | 497 |
| 18 | 23 | 600 | 13800 | 529 | 360000 | 602 |
| 19 | 4 | 528 | 2112 | 16 | 278784 | 511 |
| 20 | 11 | 538 | 5918 | 121 | 289444 | 545 |
| Всего | 125 | 10440 | 68458 | 1453 | 5469334 | 10440 |
Произведем все необходимы промежуточные расчеты:
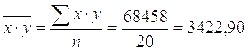 ;
;
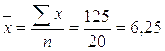 ;
;
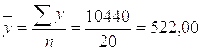 ;
;
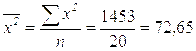 ;
;
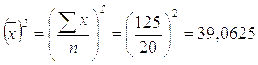 ;
;
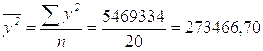 ;
;
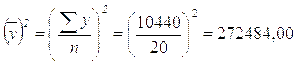
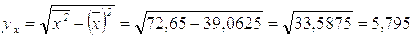
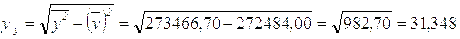
Найдем значения коэффициентов регрессии по формулам 5.2. и 5.3.:
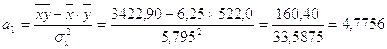
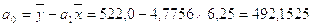
На основе выборочного уравнения регрессии получим явный вид зависимости производственного стажа рабочих цеха № 1 от заработной платы 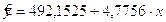
Параметр а0 представляет собой теоретическое значение результативного признака при х = 0, и показывает влияние других факторов на результативный.
Параметр а1 - коэффициент регрессии - показывает, на сколько в среднем изменяется значение признака у при увеличении значения признака х на единицу. В данном примере при повышении производственного стажа рабочих цеха № 1 на 1 полный год зарплата в среднем повышается на 4,7756 у.е. Расчет выровненного ряда указан в таблице 5.1.
По полученным величинам составляем теоретическую линию регрессии, характеризующую форму корреляционной связи между изучаемыми признаками.
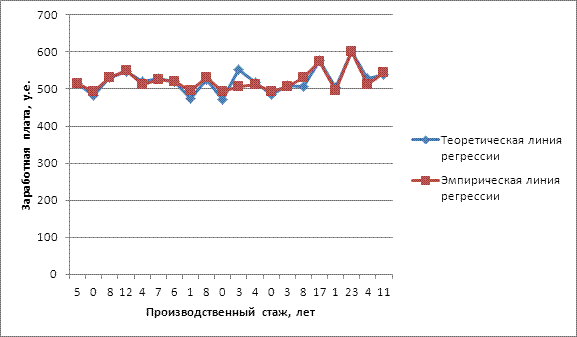
Рис.5.2. Графическое изображение зависимости производственного стажа рабочих цеха № 1 от заработной платы
5.3.Определим степень тесноты связи между рассматриваемыми признаками.
Тесноту связи в случае линейной зависимости определим на основе линейного коэффициента корреляции К.Пирсона:
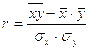 (5.4)
(5.4)
Тогда: 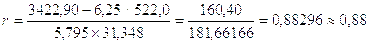
Линейный коэффициент корреляции изменяется в пределах от-1 до +1. При этом знак указывает на направление связи, а величина коэффициента, взятая по модулю - на тесноту связи.
Выводы: рассчитанный нами коэффициент корреляции указывает на прямую тесную (высокую) зависимость между производственным стажем и заработной платой рабочих завода.
Список используемой литературы:
1. Годин А.М. Статистика: Учебник.-9-е изд., перераб. и спр. – М.: Издательско-торговая корпорация «Дашков и К», 2011. – 460 с.
2. Елисеева И.И. Статистика: Учебник для вузов. - Спб.: Питер, 2010. - 368с.
3. Ефимова М.Р., Петрова Е.В., Румянцев В.Н. Общая теория статистики: Учебник. - М.: ИНФРА - М, 2010 – 416с.
4. Общая теория статистики: учебник / под ред. М. Г. Назарова. – М.: Омега-Л, 2010. - 410 с.
5. Понкратова Т.А., Кузнецова О.С. Секлецова О.В. Статистика. Общая теория статистики. Учебное пособие. – кемеровский технологичекий институт пищевой промышленности. – Кемерово, 2011. – 143с.
6. Салин В.Н. Шпаковский Е.П. Статистика:учебное пособие. – 3-е изд., - М.: КНОРУС, 2014. – 504с.
7. Статистика: учебное пособие / Харченко Л.П., Долгренкова В.Г., Ионин В.Г. и др.; под ред. к.э.н. Ионина. – М.: МНФРА-М, 2012 – 384с.
8. Статистика. Учебник/ Под ред. И.И. Елисеевой – М.: Издательств Юрайт.; ИД Юрайт, 2011 – 565с.
9. Статистика финансов: учебник / под ред. М. Г. Назарова. – 6-е изд., стер. – М.: Омега-Л, 2011. - 516 с.
10.Шмойлова Р.А. Практикум по теории статистики: Учеб. пособие. – 2-е изд.перераб. и доп. – М.: Финансы и статистика, 2006.- 416с.














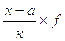
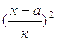
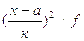
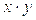
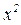
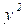
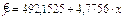
 (zip - application/zip)
(zip - application/zip)










