МІНІСТЕРСТВО ОСВІТИ І НАУКИУКРАЇНИ
Криворізький коледж
Національного авіаційного університету
МЕТОДИЧНІ ВКАЗІВКИ
з виконання курсової роботи з дисципліни:
«основи технології виробництва та ремонту повітряних суден»
на тему: «розрахунок елементів силових винтових механізмів
згинальногопреса »
Кривий Ріг 2016
Введення
Курсове завдання з розрахунку силових
гвинтових механізмів і з"єднань виконується з метою вироблення практичних
навичок у вирішенні інженерних задач по розрахунку і проектування механізмів.
Особливістю завдання є те, що при його виконанні курсантам доводиться
здійснювати перехід від розрахункових схем до реальних деталей.
В результаті розрахунку на міцність в роботі повинні бути
отримані розміри основних деталей механізму.
Всі розрахунки, креслення та необхідні пояснення поміщаються в
розрахунково -пояснювальну записку.
Розрахунково-пояснювальна записка повинна містити:
- текст завдання з вихідними даними для розрахунку і схему
механізму;
- вибір матеріалів і його обгрунтування (якщо матеріали не
задані);
- детальний розрахунок на міцність основних деталей механізму;
- визначення ККД механізму;
- список використаної літератури.
Розрахунково-пояснювальна записка виконується на стандартних
аркушах паперу розміром 210х297 мм З полями зліва шириною 20 мм. зшитих цупкою
обкладинкою. Текстова частина записки може виконуватися як в рукописній формі
так і в електронному варіанті.
Всі використані в розрахунках довідкові дані (механічні
характеристики матеріалів, допустимі напруги, різні розрахункові коефіцієнти )
повинні забезпечуватися посиланням на джерело, з якого вони взяті, із
зазначенням додатків, таблиць, графіків і т. п. Всі дані, вибрані у
відповідності з ГОСТом, повинні мати посилання на відповідний номер стандарту
(наприклад, прийнятий середній діаметр різьби d2=24.25 мм. по ГОСТу 10177-62).
Розрахунки повинні виконуватися послідовно і супроводжуватися
необхідними поясненнями. Результати кожного пункту розрахунку, а також головні
розрахункові дані коефіцієнти повинні виписуватися окремо і виділятися.
Розрахунки, як правило, слід виконувати до чотирьох знаків.
В даному методичному посібнику наводяться необхідні розрахункові
формули, послідовність розрахунку та довідковий матеріал.
Задание на курсовую работу.
1.Теоретическая часть.
Произвести описание сущности гибки металлов и ее видов,
оборудования, инструмента и приспособлений, применяемые при гибке в самолетостроении.
2.Практическая часть.
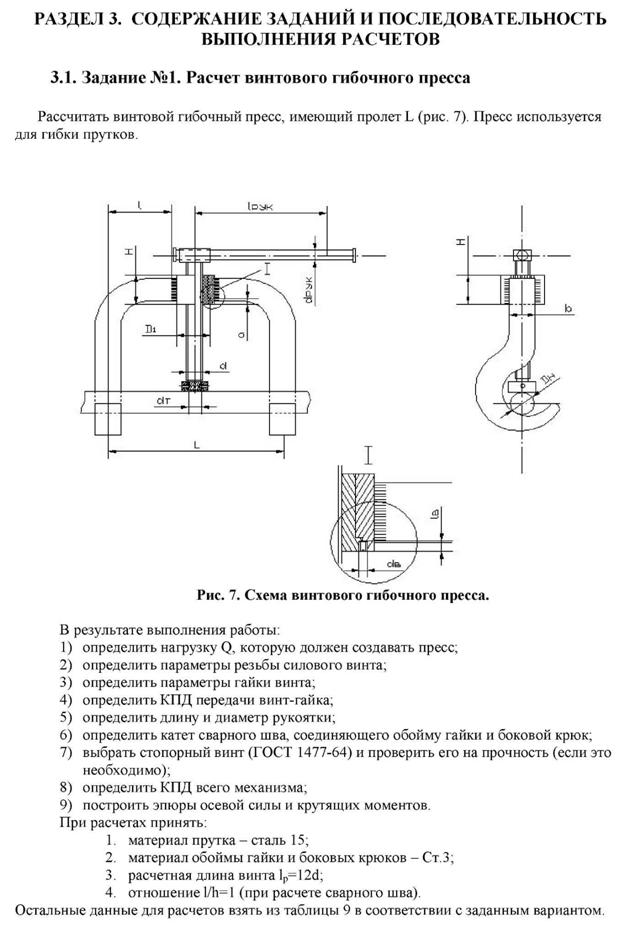
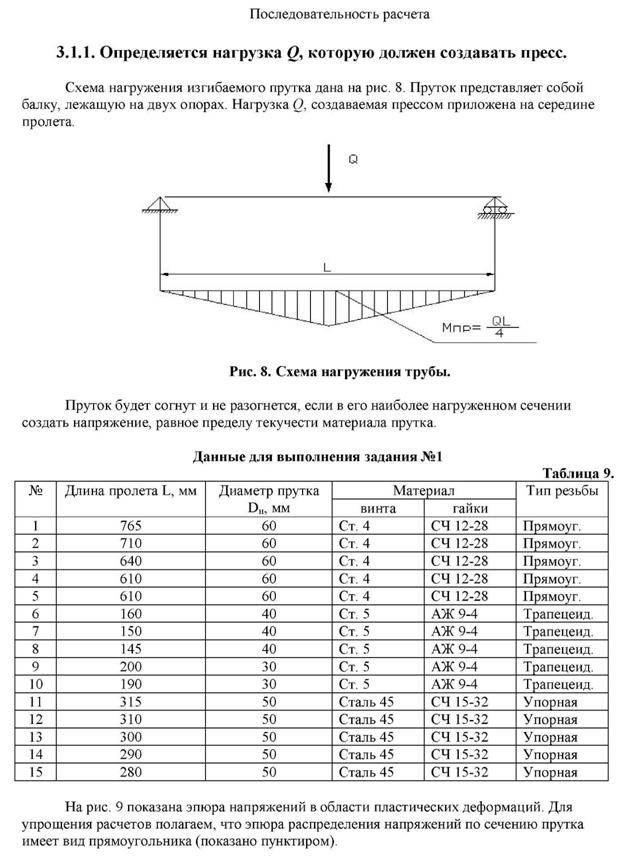
Вариант № 1 выполняет первое задание по расчету винтового гибочного пресса , имеющего пролет L, которы используется для гибки прутков.
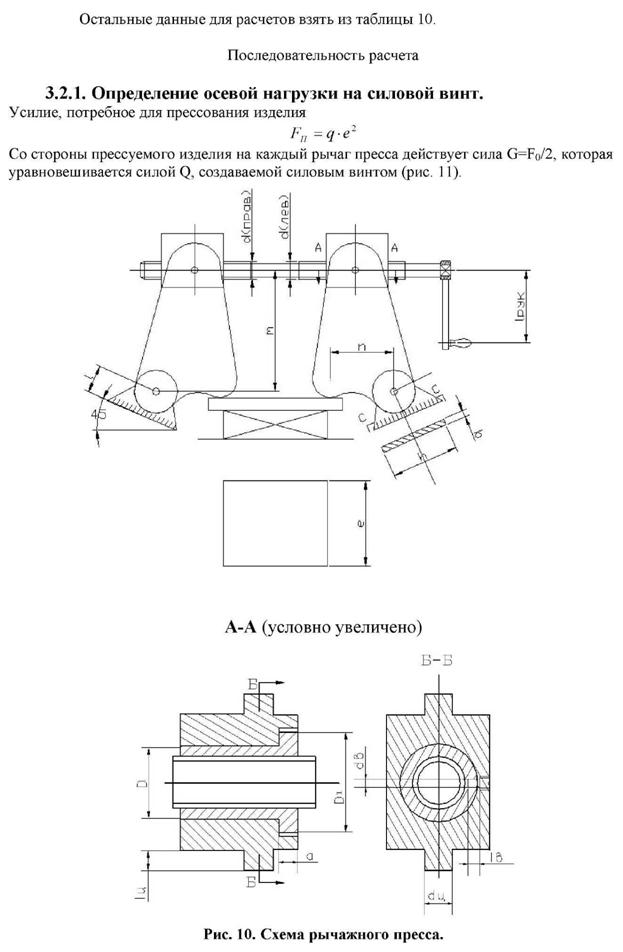
Вариант № 2 выполняет расчет винтового рычажного пресса, предназначенного для прессования изделия, имеющего форму квадрата, сторона которого равна l. Для прессования необходимо удельное давлениеq.
1. ВИНТОВЫЕ МЕХАНИЗМЫ И ОСНОВНЫЕ ТИПЫ СОЕДИНЕНИЙ
1.1. Построение эпюр продольной силы и крутящих моментов
По принципу работы винтовые механизмы можно подразделить на 4 вида:
1. механизмы, выполненные по схеме пресса (1, 3 и 7 задания);
2. механизмы, выполненные по схеме домкрата (4 и 5 задания);
3. механизмы по схеме односторонней стяжки (6 задание);
4. механизмы по схеме двухсторонней стяжки (2 задание).
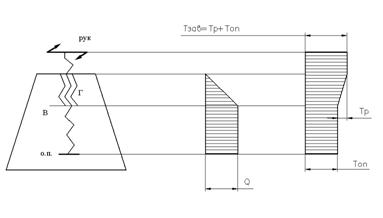
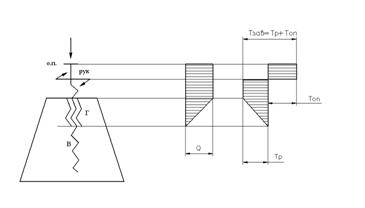
Для определения опасного сечения в винте строят эпюры продольной силы и крутящих моментов, действующих по длине винта.
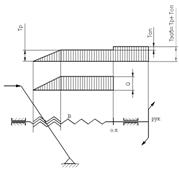
В механизмах, выполненных по схемам пресса, домкрата и односторонней стяжки, винт (В) нагружен сжимающей силой Q на участке между гайкой (Г) и опорной поверхностью (О.П.); в механизме двухсторонней стяжки винт нагружен растягивающей силой Q на участке, заключенном между двумя гайками (рис. 1).
Крутящие моменты определяются моментами в резьбе Тр и на опорной поверхности Топ. Суммарный момент равен моменту завинчивания, приложенному к рукоятке (РУК).
|
|
(1) |
По моменту завинчивания определяются размеры рукоятки.
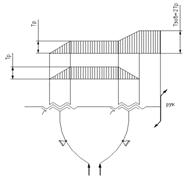
В механизме двухсторонней стяжки опорная поверхность отсутствует и момент на рукоятке равен двум моментам в резьбе, т.е.
|
|
(2) |
В этом состоит отличие механизма двухсторонней стяжки от остальных механизмов.
Момент в резьбы:
|
|
(3) |
где 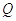 –
осевая нагрузка на винт;
–
осевая нагрузка на винт;
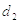 –
средний диаметр резьбы;
–
средний диаметр резьбы;
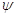 –
угол подъема винтовой линии;
–
угол подъема винтовой линии;
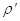 – приведенный угол
трения.
– приведенный угол
трения.
|
|
(4) |
Здесь Р – шаг резьбы.
|
|
(5) |
Здесь f – коэффициент трения в паре винт-гайка;
g – угол наклона стороны профиля.
Из формулы для определения r¢ очевидно, что для уменьшения момента трения в резьбе выгодно применять резьбы с малыми углами g. Кроме того, винты следует хорошо смазывать.
Для силовых винтов, как правило, применяются квадратная (g=0°), трапецеидальная (g=15°) и упорная (g=3°) резьбы. В случае применения упорной резьбы боковой профиль с углом 3° нужно располагать со стороны приложения нагрузки.
А
Б
|
В |
Г |
|
|
|
Рис 1. Эпюры продольных сил и крутящих моментов для механизмов: а) пресса; б) домкрата; в) односторонней стяжки; г) двухсторонней стяжки.
Момент сил трения на опорной поверхности:
|
|
(6) |
где fоп – коэффициент трения на опорной поверхности;
dпр – приведенный диаметр сил трения на опоре.
Значения диметра dпр
зависят от отношения 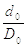 , где
, где 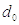 – внутренний, а
– внутренний, а 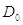 – наружный диаметр
кольцевой опоры.
– наружный диаметр
кольцевой опоры.
|
Если |
|
то |
|
|
Если |
|
то |
|
|
Если |
|
то |
|
1.2. Материалы передачи винт-гайка
Материалы силовых винтов должны обладать достаточно высокой износостойкостью и хорошо обрабатываться. Кроме того, материалы винтов должны иметь высокую прочность.
Винты, не подвергаемые закалке, обычно изготавливают из сталей марок Ст.3, Ст.4 и Ст.5, а также из сталей марок 40, 45 и 50. Наиболее распространенный материал силовых винтов – Ст.5.
Подвергаемые закалке винты выполняют из сталей 65Г, 40Х и т.п.
Основной причиной выхода из строя передачи винт-гайка является износ. Целесообразно сосредоточить износ не на винте, а на гайке, как более дешевой детали, которую легко заменить. Поэтому в передачах стальных гаек не делают.
Для гаек наиболее ответственных передач применяют оловянистые бронзы марок ОФ 10-1, ОЦС 6-6-3 и другие.
Часто применяется алюминиево-железистая бронза АЖ 9-4, как менее дефицитная.
Для гаек менее ответственных передач используют серый чугун.
1.3. Определение допускаемых напряжений
Считается, что прочность детали будет обеспечена, если выполняется условие
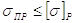
Здесь sпр – приведенное напряжение, возникающее в детали;
[s]р – допускаемое напряжение на растяжение.
Детали силовых винтовых механизмов, как правило, испытывают пульсирующую нагрузку. При такой нагрузке
|
|
(7) |
где [s]+1 и [s]-1 – значения допускаемых напряжений соответственно при статическом и знакопеременном симметричном циклах нагружений.
Допускаемое напряжение [s]+1 зависит от пластических свойств материала.
Для хрупких материалов (чугун)
|
|
(8) |
Для пластических материалов (сталь, бронза)
|
|
(9) |
Здесь sв – и sт – соответственно предел прочности и предел текучести материала;
n+1 – коэффициент запаса прочности при статической нагрузке.
Допускаемое напряжение [s], зависит от предела усталости (выносливости) материала s-1 и коэффициента запаса прочности при симметричном знакопеременном цикле нагружения n-1.
|
|
(10) |
Коэффициент запаса прочности n (n+1 или n-1) можно найти, используя метод частных коэффициентов, предложенный И.А.Одингом. Согласно этому методу коэффициент запаса прочности определяется как произведение четырех общих коэффициентов
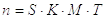
Каждый из общих коэффициентов, в свою очередь, определяется как произведение двух или трех частных коэффициентов (отсюда название метода).
S – коэффициент, учитывающий надежность материала и ответственность детали.
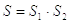
S1 – коэффициент надежности материала.
Укажем на две группы материалов, надежность которых следует различать: металлы кованные и металлы литые. В кованых металлах существующие методы испытания позволяют обнаружить дефекты, которые снижают прочность деталей более, чем на 10%. В литом же металле допускаются дефекты, которые снижают прочность детали на 30%.
Поэтому следует принимать:
- для поковки и проката S1 = 1.1;
- для литья S1 = 1.3.
S2 – коэффициент, учитывающий степень ответственности детали и ее стоимость.
Коэффициент S2 выбирается по данным таблицы 1.
Значения коэффициента S2
Таблица 1.
|
Степень ответственности |
Деталь малой стоимости |
Деталь большой стоимости |
|
Поломка детали не вызывает остановки агрегата |
1.0 |
1.0 |
|
Поломка детали вызывает остановку агрегата |
1.1 |
1.2 |
|
Поломка детали вызывает аварию |
1.2 |
1.3 |
К – коэффициент, учитывающий расчетно-конструкторские факторы.
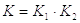
К1 – коэффициент, учитывающий точность расчетных формул и учета действующих сил.
Если расчетные формулы точны и все действующие усилия известны, то К1 = 1.
Если расчет приводит к завышенным расчетным напряжениям, то в запасе прочности следует принять также К1 = 1.
Наконец, если расчет приводит к заведомо заниженным рабочим напряжениям, то К1>1. В этом случае рекомендуется принимать К1 = 1.05 ¸1.65.
К2 - коэффициент, учитывающий концентрацию напряжений.
В соответствии с эксплуатационными и конструктивными требованиями большинство деталей машин имеют выточки, отверстия, канавки, галтели, резьбу и т.п. Эти элементы называются концентраторами напряжений.
При статической нагрузке концентраторы напряжений практически не влияют на прочность детали и коэффициент К2 = 1.
При переменной нагрузке концентраторы напряжений обуславливают появление местных напряжений, которые обычно распространяются на весьма малые объемы детали и по своей величине могут быть существенно больше номинальных напряжений. Это явление называется эффектом концентрации напряжений.
Влияние концентрации напряжений на прочность детали при переменной нагрузке учитывается при помощи эффективного коэффициента концентрации напряжений К2. При переменной нагрузке К2 > 1.
Значения коэффициента К2 при симметричном знакопеременном цикле нагружения детали могут быть заданы непосредственно при помощи таблицы или графика; например, для метрической резьбы значения К2 приведены в таблице 2.
Коэффициент К2 для метрической резьбы
Таблица 2.
|
sв МПа |
400 |
500 |
600 |
700 |
800 |
900 |
1000 |
1100 |
1200 |
|
К2 (К0) |
3.0 |
3.5 |
3.9 |
4.4 |
4.8 |
5.1 |
5.2 |
5.3 |
5.4 |
Часто в технической литературе приводятся табличные данные, графики или формулы для определения т.н. теоретического коэффициента концентрации напряжений aт. Тогда коэффициент концентрации напряжений К2 определяется по следующей формуле:
|
|
(11) |
где q – коэффициент чувствительности материала к концентрации напряжений;
для сталей q » 0.0008sв (sв в МПа)
для цветного литья q = 0.2.
для цветной поковки q = 0.3.
Примечание: для упорной, трапецеидальной и квадратной резьб aT определяется по следующей формуле
|
|
(12) |
Здесь Р – шаг резьбы;
r – радиус закругления впадин при основании резьбы.
Для упорной резьбы Р/r » 8 при любом шаге.
Для трапецеидальной и квадратной резьб
При Р = 2 ¸5 мм r = 0.25 мм;
При Р = 6 ¸12 мм r = 0.50 мм;
При Р > 12 мм r = 1.00 мм.
Если деталь выполнена из чугуна, то К2 = 1 ¸1.5. Столь малая величина К2 объясняется тем, что в чугуне имеются включения графита, представляющие собой очень острые трещины в массе металла. Влияние этих трещин настолько велико, что почти совершенно сглаживает эффект других факторов концентрации напряжений.
М – коэффициент, учитывающий метод испытания материалов.
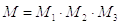
М1 – коэффициент вида деформации.
Коэффициент М1 = 1, если в формулах (8), (9) и (10) предельное (опасное) напряжение соответствует виду деформации детали. Так, если допускаемое напряжение нужно определить для случая работы детали на растяжение, то и опасные напряжения (предел прочности, предел текучести, предел усталости) должны быть взяты при растяжении; тогда М1 = 1. В противном случае М1 ¹ 1 и для определения этого коэффициента в технической литературе есть соответствующие рекомендации.
В данной работе рекомендуется всегда принимать М1 = 1 и в расчетные формулы подставить опасное напряжение, соответствующее виду деформации детали.
Предельные (опасные) напряжения для различных материалов приводятся в справочниках и руководствах (см., например, таблицу П 1).
В случае отсутствия нужных данных можно воспользоваться экспериментальными зависимостями между предельными напряжениями, приведенными в таблице 3.
М2 – коэффициент, учитывающий количество деталей, подвергнутых испытанию (проверке).
При строгой и тщательной приемке деталей, когда испытывается каждая или большое количество деталей, М2 = 1.05.
При отборочных (от партии) испытаниях, т.е. при нежесткой приемке М2 = 1.15.
М3 – коэффициент, учитывающий влияние размеров детали на ее прочность.
При статической нагрузке размеры детали на ее прочность не влияют и М3 = 1.
Если нагрузка переменная, то увеличение размеров детали понижают ее прочность. В этом случае для деталей круглого сечения при симметричном знакопеременном цикле нагружения рекомендуется пользоваться таблицей Фаульгабера (Таблица 4).
Т – коэффициент, учитывающий технологический процесс изготовления и сборки деталей и узлов.
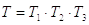
Формулы для приближенного определения механических характеристик материалов
Таблица 3.
|
При изгибе и растяжении-сжатии |
При кручении |
||
|
Стали углеродистые |
|||
|
|
|
|
|
|
Стали легированные |
|||
|
|
|
|
|
|
Чугуны серые |
|||
|
|
|
|
|
|
Цветные сплавы |
|||
|
|
|
|
|
|
sв – предел прочности при растяжении; sвсж – предел прочности при сжатии; tв – предел прочности при кручении; sт – предел текучести при растяжении; |
sти – предел текучести при изгибе; tт – предел текучести при кручении; s-1 – предел усталости при изгибе; s-1р – предел усталости при растяжении; |
||
t-1 – предел усталости при кручении.
Коэффициент М3
Таблица 4.
|
d, мм |
М3 |
|
£ 10 |
1,00 |
|
11-25 |
1,10 |
|
26-40 |
1,15 |
|
41-65 |
1,20 |
|
66-100 |
1,23 |
|
> 100 |
1,25 |
Т1 – коэффициент, учитывающий снижение прочности из-за состояния поверхности.
При статической нагрузке состояние поверхности на прочность детали не влияет и Т1=1.
При симметричном знакопеременном цикле нагружения деталей коэффициент Т1 определяется по формуле
|
|
(13) |
где а = 0 для полированной поверхности;
а = 0,0004 для шлифованной поверхности;
а = 0,0006 для поверхности, обработанной чистовым резцом;
а = 0,0010 для поверхности, обработанной обдирочным резцом;
а = 0,0017 для поверхности, не обработанной после ковки или штамповки;
а = 0,0020 для поверхностей с коррозией.
Т2 – коэффициент, учитывающий влияние на прочность детали остаточных напряжений.
Если деталь получила необходимую термообработку (отжиг, нормализация и т.п.), то Т2=1. Для деталей без термической обработки рекомендуются следующие значения коэффициента:
для поковок Т2 = 1 + 1,1;
для стального литья Т2 = 1 + 1,15;
для чугунного литья Т2 = 1 + 1,2.
Т3 – коэффициент, учитывающий напряжения при сборке и тугих посадках.
При статической нагрузке Т3 = 1.
Если нагрузка переменная, то при посадке деталей на вал с натягом в опасном сечении вала возникают высокие местные напряжения (концентрация напряжений).
При симметричном цикле нагружения И.А.Одинг рекомендует принимать значения коэффициента Т3 в зависимости от качества поверхности детали и ее материала.
для поверхности без наклепа Т3 = 2,15 + 3,30;
для поверхности с накаткой Т3 = 1,35 + 1,75;
для поверхности цементированной Т3 = 1,20 + 1,25.
Меньшие значения относятся к мягким сталям, а большие – к сталям повышенной твердости.
Из изложенного выше очевидно, что в развернутом виде коэффициенты запаса прочности определяются следующими выражениями.
При статическом нагружении
|
|
(14) |
При симметричном знакопеременном нагружении
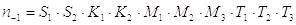
или
|
|
(15) |
2. РАСЧЕТЫ НА ПРОЧНОСТЬ ДЕТАЛЕЙ ВИНТОВЫХ МЕХАНИЗМОВ И СОЕДИНЕНИЙ
2.1. Силовой винт
Основной причиной выхода из строя передачи винт-гайка является износ.
Расчетная формула для определения среднего диаметра резьбы винта, при котором обеспечивается необходимая износостойкость передачи.
|
|
(16) |
Здесь Кр – коэффициент, зависящий от типа резьбы;
для квадратной и трапецеидальной резьб Кр = 0,8;
для упорной резьбы Кр = 0,65;
Q – осевая нагрузка на винт;
[q] – допускаемое удельное давление;
если гайка чугунная, то [q] = 5 – 6 МПа;
если гайка бронзовая, то [q] = 9 – 11 МПа;
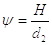 – коэффициент
высоты гайки (Н – высота гайки);
– коэффициент
высоты гайки (Н – высота гайки);
значение коэффициента y принимается по данным таблицы 5.
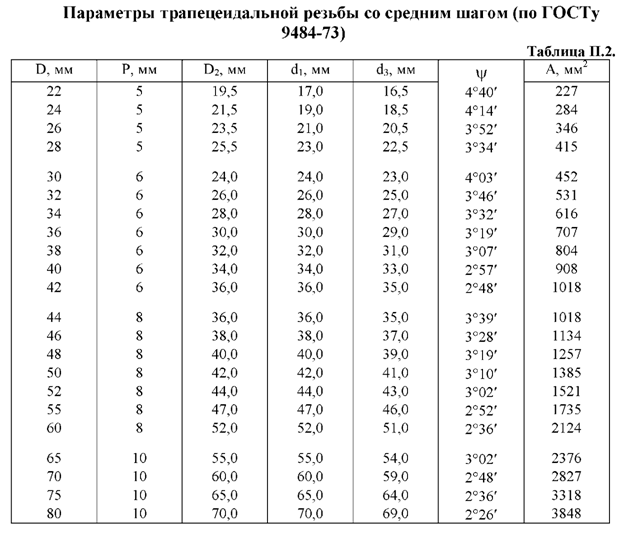
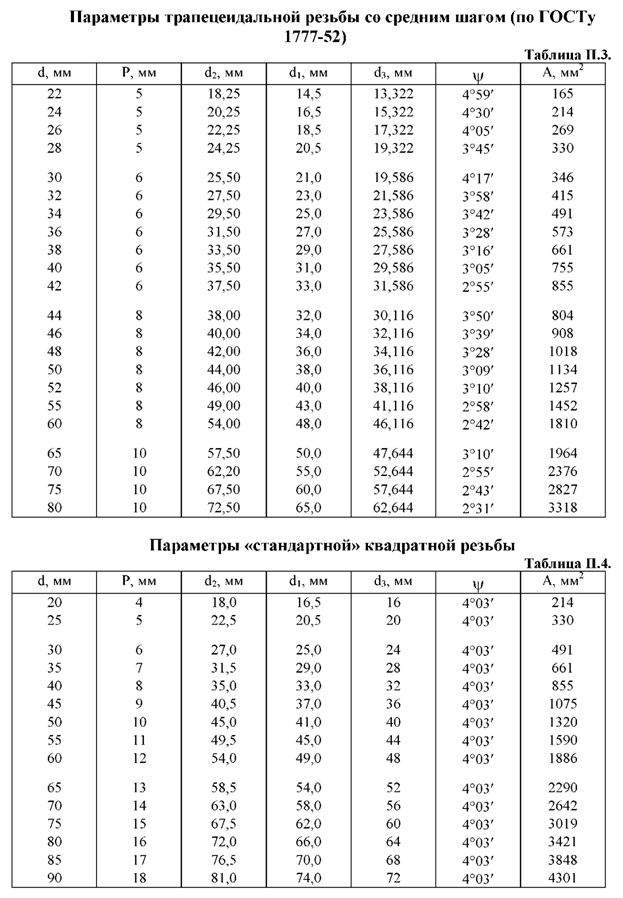
Полученное расчетом значение диаметра d2 для трапецеидальной и упорной резьб округляется до ближайшего большего стандартного значения по ГОСТ 9884-73 или ГОСТ 10177-62 (см. таблицы П2 и П3). В соответствии с d2 по ГОСТу принимаются значения наружного, внутреннего диаметра и шага.
Коэффициент y
Таблица 5
|
Тип резьбы |
Материал гайки |
|
|
Чугун |
Бронза |
|
|
Квадратная |
2,20 |
1,21 |
|
Трапецеидальная |
2,10 |
1,15 |
|
Упорная |
1,75 |
0,96 |
Квадратная резьба не стандартизована, и ее параметры определяются иначе.
Рассчитывается шаг резьбы Р
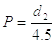
Полученное расчетом значение Р (в мм) округляется до ближайшего большего целого числа мм. Затем определяются диаметры резьбы:
наружный d = 5P;
внутренний d1 = 4P;
средний d2 = 4,5P.
Здесь Р – целое число в мм.
Рассчитанный на износ винт проверяется на прочность.
Условие прочности: sпр £ [s]р
Согласно 3-ей гипотезе прочности
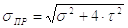
или иначе
|
|
(17) |
Здесь s - нормальное напряжение (для винта это напряжение сжатия или растяжения);
t - касательное напряжение (для винта – напряжение кручения).
Нормальное напряжение s для винта определяется по формуле
|
|
(18) |
где А1 – площадь поперечного сечения винта по резьбе;
А1 в мм2 принимается по данным таблиц П2-П4.
При отсутствии табличных данных для А1
|
|
(19) |
Значение отношения 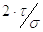 зависит от вида винтового механизма.
зависит от вида винтового механизма.
Для механизма по схеме пресса (первое, третье и седьмое задания)
|
|
(20) |
Для механизмов по схемам домкрата и односторонней стяжки (четвертое, пятое и шестое задание)
|
|
(21) |
Для механизма по схеме двухсторонней стяжки (второе задание)
|
|
(22) |
Значение угла y принимается по данным таблиц П2-П4, или (при отсутствии таблиц) определяется по формуле (4).
Приведенный угол трения в резьбе определяется по формуле (5).
При расчетах передачи винт-гайка обычно принимают f = 0,1 (среднее ходовое значение коэффициента трения в резьбе силовых винтов).
Угол наклона стороны профиля резьбы g зависит от типа резьбы (см. 1.1). Для квадратной и упорной резьб Cos(g) = 0,9659.
Следовательно, для винтов с квадратной и упорной резьбами
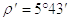
Для винтов с трапецеидальной резьбой
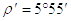
Если для винта пресса значение коэффициента трения fоп не задано, то следует принять fоп = 0,1 (среднее ходовое значение коэффициента трения в опоре). Тогда
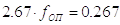
Для определения диаметра опоры dт можно использовать зависимость dт = 0,75d (если не задано другое значение dт).
Допускаемое напряжение [s]р определяется по методике, приведенной в 1.3.
Примечание. При определении отношения 2t/s для механизмов по схемам пресса и двухсторонней стяжки сделано допущение (в сторону увеличения запаса прочности), что сжимающая сила действует по всей длине винта (в частности, и в сечении, где крутящий момент Т = Тзав).
Если при проверке на прочность sпр £ [s]р, то определенные расчетом на износ размеры винта остаются без изменений.
При отрицательном результате проверки, т.е. если sпр > [s]р, следует увеличить диаметр винта и вновь выполнить расчет на прочность.
Определенные расчетом на износ и прочность размеры диаметров винта не являются окончательными, если винт испытывает сжатие. Под действием сжимающей силы винт может потерять устойчивость и разрушиться.
Необходимость и метод расчета винта на устойчивость определяются величиной гибкости винта l.
|
|
(23) |
где lр – расчетная длина винта, т.е. размер винта от середины гайки до места приложения нагрузки;
m - коэффициент длины, зависящий от способов закрепления концов винта; для винта домкрата m = 2; для винта пресса и винта односторонней стяжки m = 0.7;
d1 – внутренний диаметр резьбы.
Если l < 60, то проверку на устойчивость делать не следует, так как относительно короткие винты обычно устойчивости не теряют.
Если l = 60 ¸100, то условие устойчивости винта определяется выражением
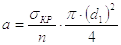
где sкр – критическое напряжение, т.е. напряжение при котором винт теряет устойчивость;
n – коэффициент надежности.
Решив последнее уравнение относительно d1, получим потребный для сохранения устойчивости внутренний диаметр винта.
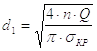
Для стальных винтов n = 3 ¸5. Обычно принимают среднее значение, т.е. n = 4. Тогда
|
|
(24) |
Критическое напряжение sкр определяется по эмпирической формуле Ф.С.Ясинского
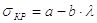 МПа
МПа
Для сталей марок 25, 30, 40, Ст. 3, Ст. 4 и подобных а = 321 и b = 1.16
Для сталей марок 45, 50, Ст. 5, Ст. 6 и подобных а = 464 и b =3.62
Если l ³ 100, то условие устойчивости винта находится на основании формулы Эйлера и может быть записано в следующем виде:
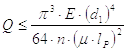
Отсюда определяется потребный для сохранения устойчивости внутренний диаметр винта
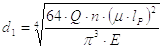
Для стальных винтов n = 4 и Е = 2.15×105 МПа. Тогда
|
|
(25) |
Здесь lр в мм и Q в Н.
Полученный в результате расчета на устойчивость диаметр d1 (после соответствующего округления) принимается в качестве параметра силового винта, если величина этого диаметра больше, чем величина d1, полученная расчетами на износ и прочность.
2.2. Определение размеров гайки
Основным расчетным параметром гайки является ее высота Н (см. рис. 2)
|
|
(26) |
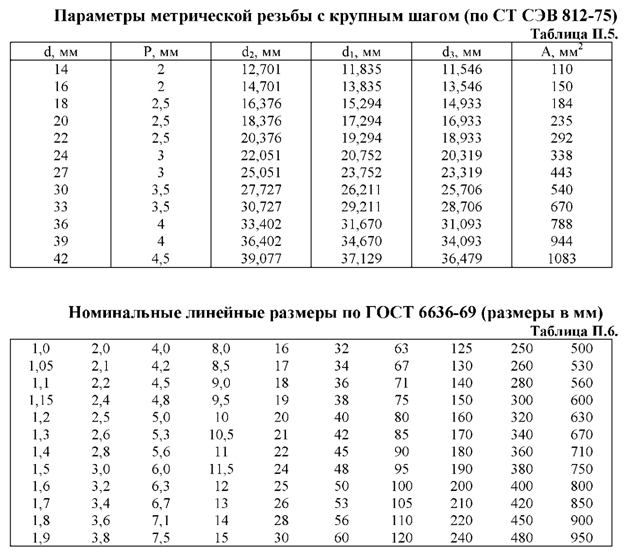
Размер Н округляется по ГОСТ 6636-69.
Число витков резьбы гайки
|
|
(27) |
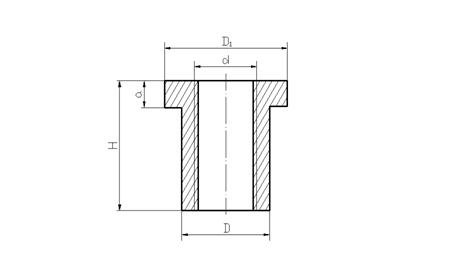
Рис. 2. Гайка силового винта.
Так как гайка выполняется из менее прочного материала чем винт, то витки резьбы гайки проверяют на изгиб.
Условие прочности витков гайки на изгиб
|
|
(28) |
В формуле (28) Ки – коэффициент, величина которого зависит от типа резьбы.
Для квадратной резьбы Ки = 1.9.
Для трапецеидальной и упорной резьб со средними шагами соответственно Ки = 1.3 и Ки = 1.5.
Допускаемые напряжения изгиба:
Для чугунных гаек [s]и = 25МПа;
Для бронзовых гаек [s]и = 40МПа.
Остальные размеры гайки (см. рис. 2) определяются конструктивно с последующей проверкой на прочность.
Наружный диаметр чугунной гайки
|
|
(29) |
Наружный диаметр бронзовой гайки
|
|
(30) |
Из технологических соображений толщину стенки гайки не делают менее 5 мм. Поэтому, если в результате расчета по формуле (29) или (30) окажется, что D < d +10мм, следует принять D = d +10мм.
Размер D (в мм) округляется по ГОСТ 6636-69.
Тело гайки проверяется на растяжение. Условие прочности
|
|
(31) |
Допускаемые напряжения растяжения:
Для чугунных гаек [s]р = 20МПа;
Для бронзовых гаек [s]р = 20МПа;
Диаметр бурта гайки
|
|
(32) |
Размер D1 (в мм) округляется по ГОСТ 6636-69.
Бурт гайки проверяется на смятие. Условие прочности
|
|
(33) |
Допускаемое напряжение смятия [s]см для чугунных и бронзовых гаек можно принять равным 60 МПа.
Высота бурта гайки
|
|
(34) |
Размер округляется по ГОСТ 6636-69.
Бурт гайки проверяется на изгиб. Условие прочности
|
|
(35) |
Допускаемые напряжения изгиба принимаются так же, как и при расчете витков гайки на изгиб.
При отрицательном результате проверки на прочность какого-либо параметра гайки этот параметр следует изменить в сторону увеличения.
2.3. Цапфы, обоймы гайки
В винтовых механизмах стяжек (задание второе и шестое) чугунная или бронзовая гайка вставляется в стальную обойму, имеющую цапфы (рис. 3). Стальная цапфа работает в отверстии детали, которую, в свою очередь, также делают стальной.
Цапфу рассчитывают на изгиб и смятие, а затем проверяют на срез.
Проектный расчет цапфы заключается в определении ее диаметра dц и длины lц.
Сначала следует определить
отношение 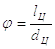 , при котором цапфа
равнопрочная по изгибу и смятию
, при котором цапфа
равнопрочная по изгибу и смятию 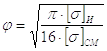
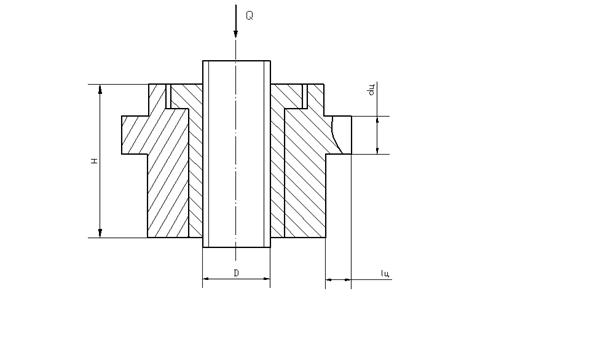
Рис. 3. Обойма гайки
Здесь [s]и – допускаемое напряжение изгиба;
[s]см – допускаемое напряжение смятия.
Так как при перемещении цапфы относительно стенки отверстия ее опорная поверхность изнашивается, то следует принимать снижение значения [s]см. Для стальных цапф можно принять [s]см ~ 0.4[s]и.
Тогда
Диаметр и длина цапфы
|
|
(36) |
|
|
(37) |
Для цапф, выполненных из сталей марок 40 и 45, допускаемое напряжение [s]и=95МПа.
Размеры dц и lц принимаются по ГОСТ 6636-69.
При определении размеров цапфы по формулам (36) и (37) условие sсм £ [s]см удовлетворяется автоматически и проверка на смятие не нужна.
Проверочный расчет цапфы – расчет на срез. Условие прочности
|
|
(38) |
Допускаемое напряжение на срез
|
|
(39) |
где sт – предел текучести материала цапфы.
При отрицательном результате проверки на срез следует увеличить диаметр цапфы и вновь выполнить проверочный расчет.
2.4. Стопорный винт
Стопорный (установочный) винт фиксирует гайку в корпусе или обойме, препятствуя ее выпаданию из механизма (например, при транспортировке). Стопорный винт также может предупреждать проворачивание гайки в случае, когда момент сил трения в резьбе винта Тр больше, чем момент сил трения на опорной поверхности бурта Тб.
Стопорные винты выполняются или с гладким цилиндрическим хвостовиком (ГОСТ 1478-64), или с плоским концом (ГОСТ 1477-64). Винт с цилиндрическим хвостовиком устанавливается в корпусе сбоку от гайки на наружном диаметре бурта (рис. 4б).
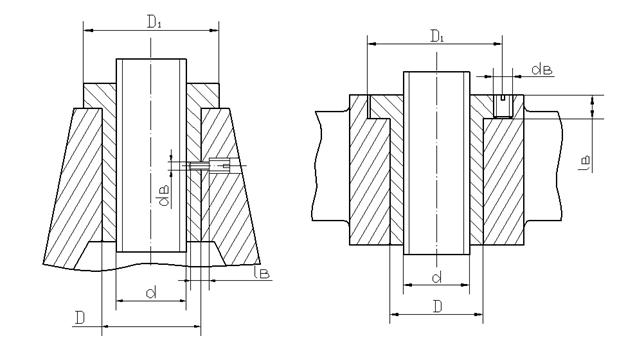
Рис. 4. Установка стопорного винта.
Размеры стопорного винта выбирают из конструктивных соображений. Обычно принимают винт М8 или М10.
Необходимость расчета на прочность соединения стопорным винтом определяется величиной момента Тп – момента, проворачивающего гайку.
|
|
(40) |
Момент Тр определяется по формуле (3) (см. 1.1)
|
|
(41) |
где fб – коэффициент трения на опорной поверхности бурта. Обычно fб = 0.15 ¸0.20.
Если Тп £ 0 (наиболее часто встречающийся случай), то соединение на прочность не проверяется. Если же Тп > 0, то соединение следует проверить на прочность.
Соединение со стопорным винтом, имеющим хвостовик, проверяется на изгиб и смятие.
На изгиб проверяют цилиндрический хвостовик винта. Условие прочности
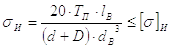
Здесь dв и lв – диаметр и длина хвостовика винта; размеры dв и lв принимаются по ГОСТ 1478-64;
[s]и – допускаемое напряжение изгиба; для винтов из сталей Ст.4 и Ст.3 [s]и=70МПа.
На смятие проверяют поверхность отверстия гайки. Условие прочности
|
|
(42) |
Допускаемое напряжение смятия [s]см для чугунной или бронзовой гайки можно принять равным 60 МПа.
При отрицательном результате проверки на изгиб или смятие следует назначить установочный винт с большим диаметром (например, вместо винта М8 принять винт М10).
Соединение с установочным винтом, имеющим плоский конец, проверяется только на смятие. На смятие проверяется поверхность бурта гайки в месте установки винта. Условие прочности
|
|
(43) |
Здесь d1в и lв – внутренний диаметр резьбы и длина винта; размеры d1в и lв принимаются по ГОСТ 1477-64.
При отрицательном результате проверки следует принять винт с большим диаметром.
2.5. Рукоятка
Рукоятка служит для передачи крутящего момента на силовой винт.
Рассчитать рукоятку – это значит определить ее длину и диаметр.
Расчетная длина рукоятки lрук определяется по формуле
|
|
(44) |
где Тзав – момент завинчивания; формулы для определения приведены в 1.1;
n – число рабочих;
K – коэффициент, учитывающий неудобство одновременной работы двух рабочих; при n = 1, K = 1, при n = 2, K = 0.9;
F – усилие, прикладываемое к рукоятке одним рабочим F = 300Н.
Полная длина рукоятки
|
|
(45) |
Размер lрук следует принять по ГОСТ 6636-69.
Примечание. Если крутящий момент на винт передается при помощи штурвала (задание третье и шестое), то радиус штурвала Rшт определяется так же, как и расчетная длина рукоятки
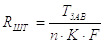
диаметр штурвала
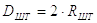
Диаметр рукоятки dрук определяют из условия прочности на изгиб
|
|
(46) |
При расчете рукоятки принимают повышенные значения допускаемого напряжения изгиба
|
|
(47) |
Здесь sт – предел текучести материала рукоятки (обычно рукоятку выполняют из стали Ст.3).
Размер dрук округляется по ГОСТ 6636-69.
2.6. Сварные соединения угловыми швами
Проектный расчет сварных угловых швов при заданных размерах детали и заданной нагрузке заключается в определении катета швов К.
В конструкциях винтовых механизмов, которые рассмотрены в данной работе, применяются два типа соединений угловыми швами.
Первый тип сварного соединения (задания четвертое и пятое) – кольцевой угловой шов, поставленный вместо бурта гайки силового винта (рис. 5). При расчете шва принимают (условно), что корпус и гайка стальные (Ст.3). Соединение нагружено силой Q и крутящим моментом Тр. Сила Q является основной нагрузкой шва, момент Тр – дополнительной (напряжение в шве от момента Тр в 8-10 раз меньше, чем от силы Q).
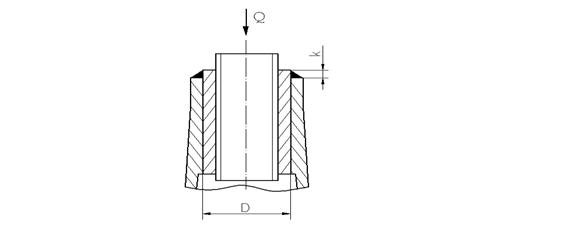
Рис. 5. Кольцевой угловой шов.
Расчет такого соединения целесообразно проводить только по основной нагрузке, а дополнительную нагрузку учитывать путем понижения допускаемого напряжения. Тогда условие прочности кольцевого шва
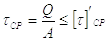
Отсюда
|
|
(48) |
Здесь А – расчетная площадь кольцевого шва;
[t]’ср – допускаемое напряжение в сварном угловом шве.
Если сварка выполняется вручную электродами обычного качества (электродами Э42 и Э50), то
|
|
(49) |
При автоматической сварке под флюсом и при ручной сварке электродами Э42А и Э50А
|
|
(50) |
В формулах (49) и (50)
sт – предел текучести основного металла (при расчете кольцевого шва основной металл – Ст.3);
n – коэффициент безопасности (при расчете только по основным нагрузкам для углеродистых сталей n = 1.45 ¸1.55);
g – коэффициент понижения допускаемых напряжений при переменных нагрузках, который для соединений, выполненных угловыми швами, вычисляется по формуле
|
|
(51) |
где r – коэффициент асимметрии цикла напряжений (при пульсирующей нагрузке r = 0).
После того, как по формуле (49) или (50) определено допускаемое напряжение [t]’ср , а затем по формуле (48) определена расчетная площадь шва А, вычисляется катет шва К
|
|
(52) |
Размер К округляется по ГОСТ 6636-69.
Второй тип сварного соединения (задание первое, второе и седьмое) – соединение втавр (впритык) угловыми швами.
Втавр соединятся элементы, расположенные во взаимно перпендикулярных плоскостях (рис. 6).
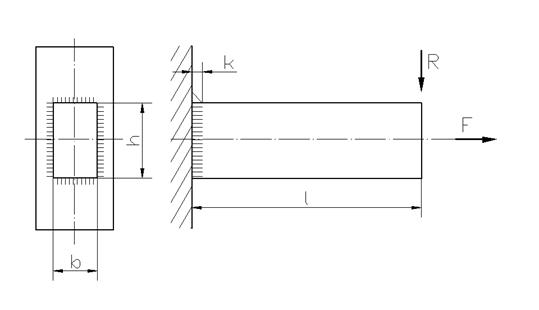
Рис. 6. Схема к расчету сварного соединения детали прямоугольного сечения (h – высота детали; b – ширина детали; k – катет шва)
При нагрузке, показанной на рис. 6 считается, что прочность соединения обеспечена, если выполняется условие
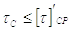
где [t]’ср – допускаемое напряжение в угловых швах;
tс – условное суммарное напряжение.
Допускаемое напряжение [t]’ср определяется по формуле (49) или (50) (в зависимости от вида технологического процесса сварки). Однако, поскольку в данном случае расчет выполняется по основным и дополнительным нагрузкам, коэффициент безопасности n=1.3¸1.4.
Условное суммарное напряжение определяется зависимостью
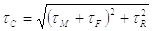
где tM – максимальное напряжение в сварных швах от изгибающего момента М (при нагрузке, показанной на рис.6, М=Rl);
tF – напряжение в швах от продольной силы F;
tR – напряжение в швах от поперечной силы R.
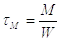
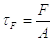
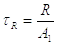
В последних трех формулах
А = 1.4 К( h + b ) – расчетная площадь сечения сварных швов;
А1 = 1.4 K h – расчетная площадь сечения вертикальных швов;
W – расчетный момент сопротивления сечения швов при изгибе.
С некоторым приближением расчетный момент сопротивления сечения швов может быть определен по формуле
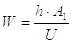
где h – высота детали (см. рис.6);
U – коэффициент, зависящий от отношения ширины детали b к ее высоте h; значения U приведены в таблице 6.
Значения коэффициента U.
Таблица 6.
|
b/h |
0,25 |
0,50 |
0,75 |
1,00 |
1,25 |
1,50 |
|
U |
3,82 |
2,57 |
1,92 |
1,55 |
1,29 |
1,11 |
С учетом изложенного выше, условие прочности сварного соединения втавр
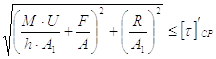
Отсюда 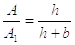 получаем формулу для
определения расчетной площади вертикальных швов
получаем формулу для
определения расчетной площади вертикальных швов
|
|
(53) |
Зная расчетную площадь вертикальных швов А, нетрудно определить катет швов К
|
|
(54) |
Размер К округляется по ГОСТ 6636-69.
При выполнении проектного расчета сварного соединения втавр момент сопротивления при изгибе W был определен приближенно. Поэтому для страховки целесообразно сделать проверочный расчет соединения. Условие прочности
|
|
(55) |
При выполнении проверочного расчета момент W следует определить точно
|
|
(56) |
Если результат проверки отрицательный (случай весьма редкий), то нужно увеличить катет швов, приняв следующий большой размер К по ГОСТ 6636-69 и вновь выполнить проверочный расчет.
Примечание. Если при проверке соединения на прочность tс>[t]’cp, но tс отличается от [t]’cp менее, чем на 5%, то катет швов увеличивать не следует, т.к. перегрузкой в 5% можно пренебречь.
2.7. Резьбовые соединения
Прочность болта или шпильки при постоянной рабочей нагрузке обеспечена, если выполняется условие
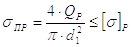
где sпр – приведенное напряжение в болте (шпильке);
Qp – расчетная нагрузка на болт (шпильку);
d1 – внутренний диаметр резьбы;
[s]p – допускаемое напряжение на растяжение.
Допускаемое напряжение на растяжение для резьбовых соединений назначается в зависимости от предела текучести материала болта или шпильки
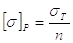
где n – допускаемое значение коэффициента запаса прочности (допускаемый запас прочности) по пластическим деформациям.
Отсюда условие прочности болта (шпильки)
|
|
(57) |
Для соединения с неконтролируемой затяжкой болтов (шпилек), выполненных из углеродистой стали (такие соединения рассматриваются в заданиях третьем и шестом), значения допускаемого запаса прочности n рекомендуется вычислять по следующим формулам:
|
при d = 6…16 |
|
(58) |
|
при d = 16…30 |
|
(59) |
|
при d = 30…60 |
|
(60) |
Здесь d – наружный диаметр резьбы в мм.
Проектный расчет резьбового соединения заключается в определении внутреннего диаметра резьбы. Остальные параметры резьбы определяются по ГОСТу.
Согласно уравнению (57)
|
|
(61) |
При проектном расчете соединения с неконтролируемой затяжкой болтов использовать формулу (61) нельзя, т.к. допускаемый запас прочности зависит от наружного диаметра резьбы d, который при проектном расчете неизвестен. Поэтому рекомендуемая последовательность расчета приведена ниже.
1. Внутренний диаметр резьбы d1 определяется приближенно
|
|
(62) |
Значения коэффициента Кт принимаются по данным таблицы 7.
Полученный расчетом диаметр d1 округляется до большего стандартного значения по СТ СЭВ 182-75, по СТ СЭВ принимается соответствующий наружный диаметр резьбы d.
2. Выполняется проверочный расчет болта или шпильки, размеры которых уже определены.
Если sпр £ sт / n, то расчет окончен и первоначально принятые размеры резьбы остаются без изменений.
При отрицательном результате (sпр > sт / n) следует увеличить диаметр болта – принять болт (шпильку) со следующим большим стандартным диаметром (например, вместо болта М12 принять болт М14).
Значения коэффициента Кт для соединений, выполненных из углеродистых сталей
Таблица 7.
|
Qр / sт |
Кт |
|
св. 4,7 – 14,8 |
2,17 |
|
св. 14,8 – 32 |
2,10 |
|
св. 32 – 82 |
1,91 |
|
св. 82 – 183 |
1,76 |
|
св. 183 – 390 |
1,60 |
|
св. 390 – 730 |
1,48 |
|
св. 730 – 1300 |
1,38 |
|
св. 1300 – 1760 |
1,29 |
При переменной рабочей нагрузке осевое усилие, действующее на болт (шпильку), изменяется в пределах от Qmin до Qmax. Соответственно, приведенное напряжение изменяется в пределах от Qmin до Qmax. Статическая прочность соединения при переменной рабочей нагрузке обеспечена, если
|
|
(63) |
Здесь Qpmax – максимальная расчетная нагрузка на болт (шпильку).
Допускаемый запас прочности n назначается так же, как для соединений, работающих при постоянной нагрузке, т.е. вычисляется по формулам (58) – (60).
Полное приведенное напряжение в болте, работающем при переменно нагрузке, можно разделить на постоянное (среднее) напряжение sm и переменное с амплитудой sа.
Среднее напряжение
|
|
(64) |
Амплитуда напряжений
|
|
(65) |
Запас прочности резьбового соединения по переменным напряжениям (запас усталостной прочности) na определяется по формуле
|
|
(66) |
где sв – предел прочности материала болта;
s-1р –предел усталости материала болта при растяжении;
Ks – эффективный коэффициент концентрации напряжений. Значения кs для метрической резьбы даны в таблице 2;
e – масштабный коэффициент, значения которого даны в таблице 8.
Значения коэффициента e
Таблица 8.
|
d в мм |
16 |
18 |
20-24 |
27-33 |
36-42 |
45-52 |
56-64 |
|
e |
1 |
0,9 |
0,78 |
0,7 |
0,64 |
0,6 |
0,55 |
Условие прочности болта и шпильки, работающих при переменной нагрузке,
na ³ 2,5
Итак, проверочный расчет болтов (шпилек), работающих при переменной нагрузке, состоит в определении приведенного напряжения smax и запаса прочности na и сравнении этих величин с допускаемыми.
При проектном расчете резьбового соединения с переменной рабочей нагрузкой внутренний диаметр резьбы d1 предварительно назначается на основании формулы
|
|
(67) |
Значения коэффициента Кт
для болтов с неконтролируемой затяжкой принимается по данным таблицы 7 в
зависимости от отношения 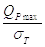 ..
..
После того, как диаметр d1 определен и округлен по СТ СЭВ 182-75 до большего стандартного значения, выполняется проверочный расчет соединения по методике, изложенной выше.
При отрицательном результате проверки, то есть если smax > sт/n или nа < 2,5, увеличивается диаметр резьбы (принимается болт или шпилька со следующим большим стандартным диаметром).






Литература
- Ачеркян Н.С. (редактор) Детали машин, т.1.-М.; Машиностроение, 2008.
- Биргер Н.А., Шорр Б.Ф., Шнейдерович Р.М. Расчет на прочность деталей машин,-М.; Машиностроение, 2006.
- Бондаровский Ф.П., Корнеев Г.В., Детали машин и подъемно-транспортные машины,-М.; Машгиз, 2002.
- Борисов В.В, Метелкин В.В. и др. Расчет силовых винтовых механизмов и соединений,-М.; МАТИ, 2005.
- Дашкевич Б.П., Дьяченко С.К., Столбовой С.З. Детали машин, М., ГИТЛ УССР, 1959.
- Добровольский В.А, Заблонский К.И. и др. Детали машин,-М.; Машгиз, 1957.
- Иванов М.Н. Детали машин.,-М.; Высшая школа, 1976.
- Одинг И.А. Допускаемые напряжения в машиностроении и циклическая прочность металлов.-М.; Машгиз, 2002.
- Поляков В.С., Кудрявцев В.Н. и др. Детали машин,-М.; Машгиз, 2008.
- Решетов Д.Н. Детали машин.-М.; Машиностроение, 2004.
- Справочник металлиста.-М.; Машгиз, 1958
- Чистяков А.А. Методика выполнения курсовых домашних работ по деталям машин.-М.; МАТИ, 2003.














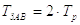
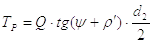
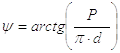
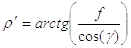
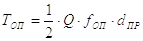
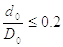 ,
,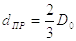 .
.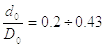 ,
, .
.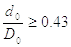 ,
,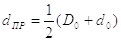 .
.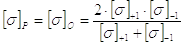
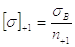
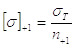
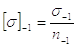
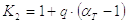
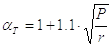
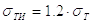
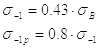
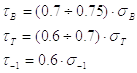
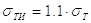
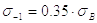 +
120 MПа
+
120 MПа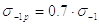
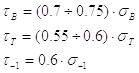
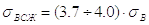
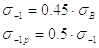
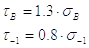
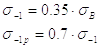
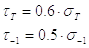
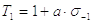 ,
, 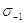 - [МПа]
- [МПа]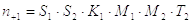
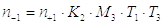
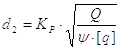
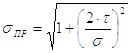
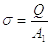
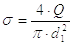
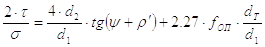
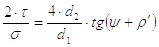
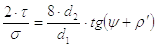
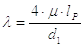
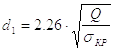
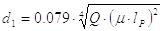 мм
мм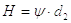
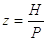
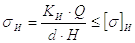
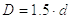
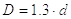
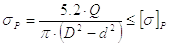
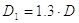
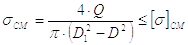
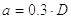
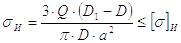
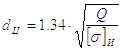
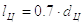
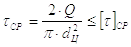
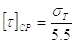
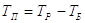
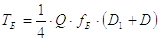
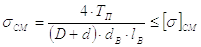
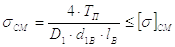
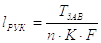
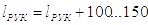 мм
мм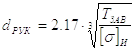
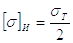
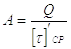
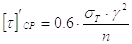
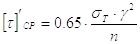
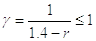
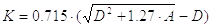
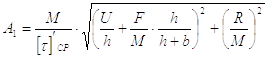
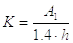
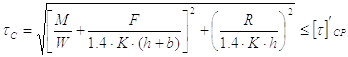
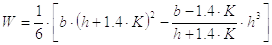
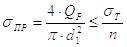
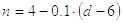
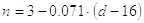
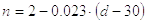
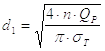
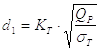
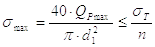
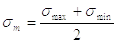
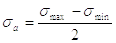
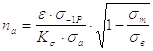
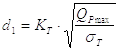
 (zip - application/zip)
(zip - application/zip)










