раціональні, ірраціональні, дійсні числа, числові множини та етапи розвитку числа

Реферат

На тему :

«раціональні, ірраціональні,

дійсні числа, числові множини

та етапи розвитку числа»

Виконав

учень 8-а класу

Пустомитівської ЗОШ №1

Теглівець Олександр

Ірраціональні числа

Ірраціональні числа — числа, що не є раціональними, тобто не можуть бути виражені відношенням цілих чисел. Таким чином, ірраціональні числа утворюють множину , де  — множина дійсних чисел, а  — множина раціональних чисел. 

Уперше виникли в геометрії при вивченні довжин. Геометрично ірраціональне число виражає собою довжину відрізка, неспівмірного з відрізком одиничної довжини. За легендою, піфагорейці відкрили несумірність деяких геометричних величин, але оскільки це суперечило їх філософії, цілком побудованій на натуральних числах, вони утримували це відкриття у найсуворішій таємниці і навіть покарали на смерть одного з членів свого братства, який (за різними джерелами) чи першим знайшов, чи розголосив цей факт.

Раціональні числа при записі їх у десятковий дріб мають періодично повторювану частину. Наприклад:

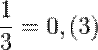   де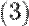 означає, що трійка повторюється нескінчену кількість раз, довжина періоду — один.

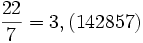, довжина періоду — шість.

Періодичність дробу можна вважати за критерій приналежності числа до раціональних чисел. При розкладанні ірраціональних чисел у десятковий дріб не спостерігається такої періодичності. Наприклад, відомо, що число пі  — ірраціональне, і навіть трансцендентне. Тому, хоча в його десятковому записі окремі цифри та комбінації цифр повторюються, не існує групи цифр, яка б нескінченно повторювалася, утворюючи період.

Існує інший спосіб задання додатних дійсних чисел: за допомогою ланцюгових дробів. У цьому разі, різниця між раціональними та ірраціональними числами полягає в тому, що ланцюгові дроби раціональних чисел скінченні, а ірраціональних нескінченні, хоча для квадратичних ірраціональностей ланцюговий дріб періодичний. Приклади:

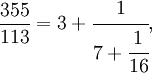
скінченний;

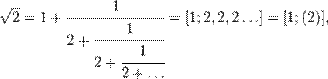
з періодом довжини один;

 

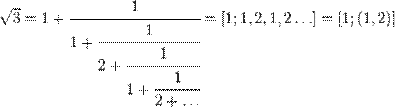
з періодом довжини два;

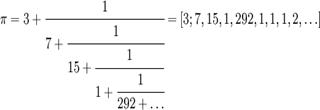
Про існування неспівмірних відрізків знали вже древні математики: їм була відома, наприклад, неспівмірність діагоналі та сторони квадрата, що рівносильно ірраціональності числа  (перше знайдене ірраціональне число).

Піфагорове твердження, що всі речі є числа, відображало метафізичні уявлення стародавніх греків. Всесвіт є місцем гармонії, а гармонію, в свою чергу, можна описати відношенням натуральних чисел. Так поєднання двох звуків, відношення частот яких є раціональне число, дає приємне для вуха звучання. Відкриття того, що довжина діагоналі квадрата зі сторонами довжиною 1, тобто , не є раціональним числом, призвело до глибокої кризи давньогрецької математики.

Криза полягала в усвідомлені факту існування математичних величин, які не можуть бути виражені числами. Але ті самі математичні величини можуть бути виражені через геометричні побудови. Як наслідок — давньогрецька математика відмовилась від алгебраїчного підходу, на користь геометричного.

Властивості:

Всяке дійсне число може бути записане нескінченим десятковим дробом, при цьому ірраціональні числа і тільки вони записуються неперіодичними десятковими дробами.

Кожне ірраціональне число визначає такий переріз Дедекінда у множині раціональних чисел, для якого в нижньому класі немає найбільшого, а у верхньому класі немає найменшого раціонального числа.

Кожне ірраціональне число є або алгебраїчним, або трансцендентним, а кожне трансцендентне число є ірраціональним.

Множина ірраціональних чисел скрізь щільна на числовій прямій, тобто між будь-якими двома дійсними (і навіть раціональними) числами є ірраціональне число (і навіть нескінченно багато ірраціональних чисел).

Множина ірраціональних чисел — незліченна множина другої категорії.

Раціональні числа

Раціональні числа — в математиці множина раціональних чисел ℚ визначається як множина нескоротних дробів із цілим чисельником і натуральним знаменником:

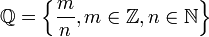
або як множина розв"язків рівняння

 

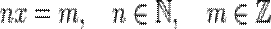
тобто n — натуральне число, m — ціле число.

Множина раціональних чисел є підмножиною алгебраїчних та дійсних чисел.

Формальне означення

Можна дати формальне означення раціональних чисел як множини класів еквівалентності    пар 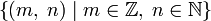 за відношенням еквівалентності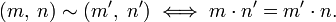

При цьому операції додавання й множення визначаються так:

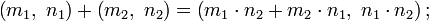
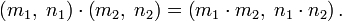
Пов"язані означення:

Правильним зветься дріб, в якого модуль чисельника менший за модуль знаменника.

Дріб, який не є правильним, зветься неправильним.

Наприклад, дроби  ; та є правильними, а  ; та є неправильними.

Будь-яке ціле число можна подати в вигляді неправильного дробу зі знаменником 1.

Дріб, записаний як ціле число й правильний дріб, зветься змішаним дробом й розглядається як сума цього числа та дробу.

Наприклад,.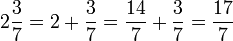

У строгій математичній літературі запис у вигляді змішаного дробу переважно не використовується через подібність позначення змішаного дробу з позначенням добутку цілого числа з дробом.

Властивості

Основні властивості

Для раціональних чисел виконуються шістнадцять основних властивостей, які можна отримати з властивостей цілих чисел.[1]Впорядкованість. Для будь-яких раціональних чисел  та  існує правило, яке дозволяє однозначно ідентифікувати між ними одне й тільки одне з трьох відношень: «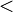», «» 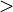або «». Це правило зветься правилом впорядкування

Дійсні числа

Дійсні числа — елементи певної числової системи, яка містить у собі раціональні числа і, в свою чергу, є підмножиною комплексних чисел.

Дійсні числа утворюють поле, яке позначається  (від англ. real, нім. reel). Це означає, що дійсні числа можна додавати, віднімати, множити та ділити (окрім ділення на нуль), і для них справджуються всі звичні властивості арифметичних дій (комутативність і асоціативність додавання та множення, дистрибутивність додавання та віднімання відносно множення тощо).

На відміну від раціональних чисел, множина дійсних чисел є замкненою відносно операції граничного переходу. Тому вчення про дійсні числа належить до математичного аналізу.

Символ яким

найчастіше позначають

множину дійсних чисел.

Вже давні греки помітили потребу розглядати ірраціональні числа (тобто дійсні числа, які не є раціональними). Наприклад, ірраціональним є відношення довжини діагоналі квадрата до довжини його сторони, яке ми позначаємо  Інтуїтивний зміст ірраціональних чисел полягає в тому, що вони заповнюють "дірки", що залишаються на числовій осі між раціональними числами; множина дійсних чисел є поповненням множини раціональних чисел. Перше математично строге означення дійсних чисел було винайдено лише наприкінці 19 століття.

Числові множини

Обмежена множина у математичному аналізі, і прилеглих розділах математики — множина, яка у певному сенсі має скінченний розмір. Базовим є поняття обмеженості числової множини, яке узагальнюється на випадок довільного метричного простору, а також на випадок довільної частково упорядкованої множини. Поняття обмеженості множини не має сенсу у загальних топологічних просторах, без метрики.

Множина дійсних чисел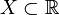 називається обмеженою зверху, якщо існує число 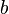, таке що всі елементи не перевищують:

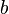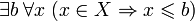
Множина дійсних чисел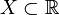 , обмежена зверху і знизу, називається обмеженою.

Множина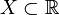, що не є обмеженою, називається необмеженою. Як випливає з означення, множина не обмежена тоді і тільки тоді, коли вона не обмежена зверху або не обмежена знизу.

Прикладом обмеженої множини є відрізок,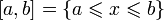

необмеженої — множина всіх цілих чисел,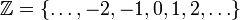

обмеженої зверху, але необмеженої знизу — промінь,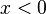

обмеженої знизу, але необмеженої зверху— промінь.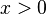

Варіації та узагальнення

Обмежена множина у метричному просторі

Нехай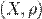 — метричний простір. Множина 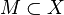називається обмеженої, якщо вона міститься у деякій кулі:

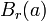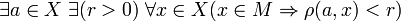
Множина, що не є обмеженою, називається необмеженою.

На відміну від числової прямої, у довільному метричному просторі можна ввести поняття обмеженої зверху і обмеженої знизу множин.Крім поняття обмеженої множини для довільного метричного простору існує більш спеціальне поняття цілком обмеженої множини. У випадку числових множин це поняття збігається з поняттям обмеженої множини.Обмеженість у частково впорядкованій множині

Поняття обмеженої зверху, обмеженої знизу і просто обмеженої множини можна ввести у довільній частково впорядкованій множині. Ці визначення буквально повторюють відповідні визначення для числових множин.

Нехай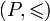 — частково впорядкована множина, 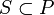. Множена  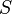називається обмеженою зверху, якщо 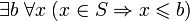обмеженою знизу, якщо 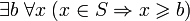Множина, обмежена і зверху і знизу, називається обмеженою

Етапи розвитку числа.

Натура́льні чи́сла — числа, що виникають природним чином при лічбі. Це числа: 1, 2, 3, 4, … Множину натуральних чисел прийнято позначати знаком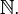

Існують два основних підходи до означення натуральних чисел:

числа, що використовуються при лічбі предметів (перший, другий, третій…) — підхід, загальноприйнятий у більшості країн світу; формалізованим різновидом цього підходу є аксіоматичне описання системи натуральних чисел за допомогою аксіом Пеано.

числа для позначення кількості предметів (відсутність предметів, один предмет, два предмети…) — підхід, прийнятий у роботах Ніколя Бурбакі, де натуральне число означається як потужність скінченних множин; при такому підході, як правило, 0 відносять до натуральних чисел. Від"ємні та дробові числа не є натуральними числами.

Множина натуральних чисел є нескінченною: для будь-якого натурального числа знайдеться інше натуральне число, більше за нього.

Історія натуральних чисел

Поняття натурального числа, викликане потребою лічби предметів, виникло ще в доісторичні часи. Процес формування поняття натурального числа тривав протягом усієї історії людства. На найнижчому етапі первісного суспільства поняття абстрактного числа не існувало. У свідомості первісної людини ще не сформувалося те спільне, що об"єднує наприклад, «три людини» та «три озера». Аналіз мов первісних народностей показує, що для лічби предметів різного типу використовувалися різні словесні обороти. Слово «три» в контекстах «три людини», «три човни» передавалося по-різному. Такі іменовані числові ряди були дуже короткими і завершувалися неіндивідуалізованим поняттями «багато», які також були іменованими, тобто висловлювалися різними словами для різних типів об"єктів, такими, як «натовп», «стадо», «купа» тощо.

Спочатку числові терміни мали якісніший характер — відрізняли один, два та більшу кількість. Більші числа одержували додаванням. Наприклад, в австралійського племені ріки Муррей, 1 — енза, 2 — петчевал, 3 — петчевал-енза, 4 — петчевал-петчевал. Але навіть такі здібності людство здобуло після великого проміжку часу, в який користувалися лише з понять «один», «два» та «багато» (ще й досі збереглося плем"я, яке зупинилося на цьому етапові розвитку вмінь числового абстрагування).

Джерелом виникнення поняття абстрактного числа була лічба предметів, що базувалася на зіставленні предметам даної сукупності предметів певної сукупності, що мала роль еталону. У більшості народів першим таким еталоном були пальці («лічба на пальцях»), що безпосередньо підтверджується мовознавчим аналізом назв перших чисел. На цьому етапі число стає абстрактним, незалежним від якості об"єктів лічби, але разом з тим пов"язаним з природою сукупності-еталону. Розширення потреб лічби спонукало людей користуватися з інших еталонів лічби, наприклад, зарубок на паличці. Для фіксації порівняно великих чисел стала використовуватися нова ідея: позначення деякого певного числа (у більшості народів — десяти) новим знаком, наприклад, зарубкою на іншій паличці.

З розвитком писемності можливості відтворення чисел значно розширились. Спочатку числа стали позначати рисками на матеріалі, що слугував для запису (папірус, глиняні таблички тощо). Потім були введені інші знаки для великих чисел. Вавилонські клинописні позначення чисел, а також «римські цифри», що збереглися до наших днів, ясно свідчать саме про цей шлях формування позначень для чисел.

Великим прогресом було винайдення «цифр». Тепер стало можливим записати будь-яке число обмеженим набором символів. Наприклад, вавилоняни розвинули потужну позиційну систему, що базувалася на цифрах 1 та 10, але фактично її основою було число 60. Зручнішою була індійська позиційна система числення, що дозволяла записати будь-яке натуральне число за допомогою десяти знаків — цифр; вона згодом стала всесвітньо визнаною і досі залишається такою (хоча форма цифр дещо змінювалася; цифри цієї системи ми називаємо арабськими, оскільки система прийшла в Європу через арабів). Таким чином, паралельно з розвитком писемності, поняття натурального числа приймає все більш абстрактну форму, відокремлену від будь-якої конкретності поняття числа, відтворюваного як у формі слів в усній мові, так і в формі позначення спеціальними знаками в письмовій.

Важливим кроком у розвитку поняття натурального числа є усвідомлення нескінченності натурального ряду чисел — потенційної можливості його безмежного продовження. Чітке уявлення про нескінченність натурального ряду відображене в пам"ятниках античної математики (III століття до н.е.), у працях Евкліда й Архімеда. У «Началах» Евкліда встановлюється навіть нескінченність кількості простих чисел, а у книзі Архімеда «Псаміт» — принципи для побудови назв та позначень як завгодно великих чисел, зокрема більших за «число піщинок у світі».

Нуль, спочатку означав відсутність числа; він став розглядатися як число лише після введення від"ємних чисел нуль іноді включають до натуральних чисел).

Питання про обґрунтованість поняття натурального числа довгий час у науці не ставилося. Поняття натурального числа настільки звичне і просте, що не виникало потреби в його означенні в термінах будь-яких простіших понять. Лише в середині XIX століття, під впливом розвитку аксіоматичного методу в математиці з одного боку, і критичного перегляду основ математичного аналізу — з іншого, назріла необхідність обґрунтування поняття кількісного натурального числа.

Чітке означення поняття натурального числа на основі поняття множини було дано в 70-х роках XIX століття в роботах Георга Кантора. Спочатку він означує рівнопотужність множин. Потім число елементів однієї множини означається як те спільне, що має дана множина і будь-яка інша, рівнопотужна їй, незалежно від якісних особливостей елементів цих множин. Таке означення відображає суть натурального числа як результату лічби предметів.

Інше обґрунтування поняття натурального числа базується на аналізі відношення порядку слідування, яке може бути задано за допомогою аксіом. Побудована на цьому принципі система аксіом була сформульована Джузеппе Пеано.

Аксіоми Пеано

Формальне означення натуральних чисел сформулював італійський математик Джузеппе Пеано в 1889 році. Аксіоми Пеано базувалися на розробках Грассмана, хоча саме Пеано надав їм сучасного вигляду. Ці аксіоми дозволили формалізувати арифметику. Після їх введення з"явилася можливість доводити, наприклад, рівність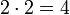, основні властивості натуральних чисел, а також формалізовано будувати системи цілих, раціональних, дійсних чисел.

Аксіоми Пеано:

Введемо функцію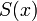 котра зіставляє числу  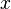наступне за ним число (інакше кажучи, число, що слідує за ним).

1.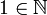 (одиниця є натуральним числом).

2.Якщ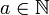о  то 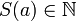 (число, наступне за натуральним, також є натуральним).

3.

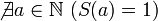
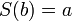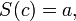4.Якщо  та  то 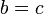 (натуральне число не може слідувати за двома різними натуральними числами).