произвести анализ и синтез АСУ с помощью пакета MATLAB

Федеральное государственное автономное

образовательное учреждение высшего образования

«СИБИРСКИЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ»

Институт цветных металлов и материаловедения

Кафедра автоматизации производственных процессов и теплотехники в металлургии

КУРСОВОЙ ПРОЕКТ

Преподаватель             _____________________     А.А. Дружинина

подпись, дата

Студент     ЦМ15-15   _____________________     А.А. Потапчик

подпись, дата

Красноярск 2016

Цель работы: произвести анализ и синтез АСУ с помощью пакета MATLAB.

Исходные данные: вариант №6

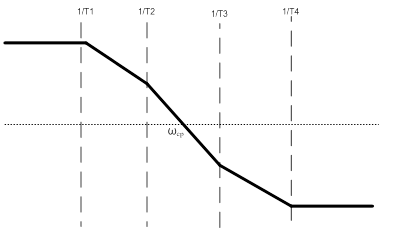
Рисунок 1 – Исходные данные АСУ

ω_ср = 444 с^-1

K = 120

Заданные показатели качества

Ход работы:

По виду ЛАЧХ определяем вид передаточной функции АСУ W(p):

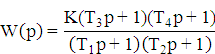
Подбираем значения постоянных времени, T₁,T₂,T_3,T₄:

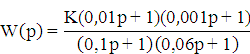
Строим ЛАЧХ полученной АСУ (рисунок 2):

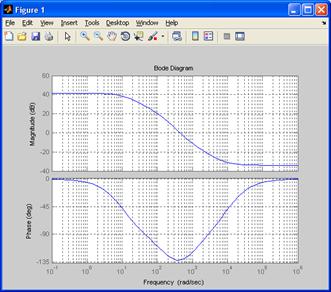
Рисунок 2 – Графики ЛАЧХ полученной АСУ

Определяем корни характеристического уравнения разомкнутой системы:

p₁ = -166,6667;

p₂ = -10,0000.

Так как корни вещественные и отрицательные, то для устойчивой системы в замкнутом состоянии годограф Найквиста не должен охватывать точку с координатами [-1;j0].

Строим годограф Найквиста (рисунок 3 и 4):

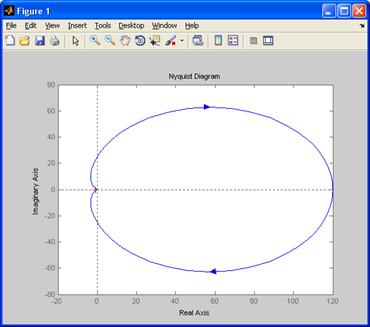
Рисунок 3 – годограф Найквиста (общий вид)

[-1;j0]

 

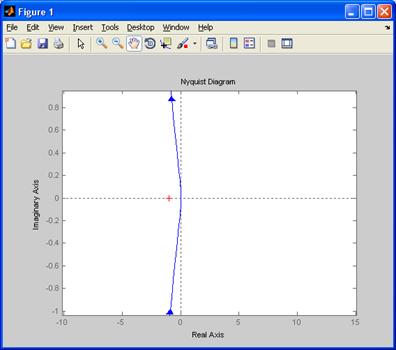
Рисунок 4 – годограф Найквиста (увеличение в точке [-1;j0])

Так как годограф Найквиста не охватывает точку с координатами [-1;j0], то АСУ устойчива.

Получим передаточную функцию (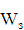) замкнутой системы:

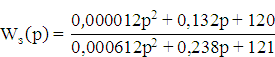
Определяем корни характеристического уравнения замкнутой системы:

p₁ = -1,9444 + 3,9988i;

p₂ = -1,9444 – 3,9988i.

Так как корни комплексные и имеют отрицательную вещественную часть, то система устойчива.

Строим переходный процесс в системе (рисунок 5):

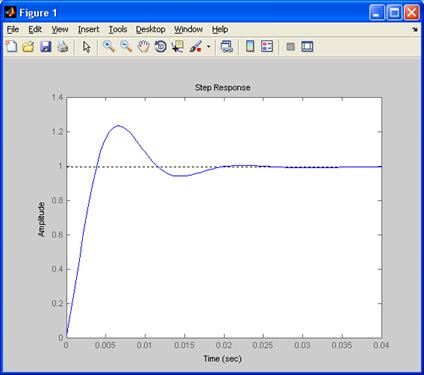
Рисунок 5 – Переходный процесс в замкнутой системе

Определяем показатели качества:

Максимальное динамическое отклонение, x_макс:

 

x_макс = 1,23

 

Время регулирования, t_р:

t_р = 0,02 с

Перерегулирование, σ:

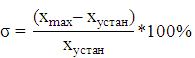
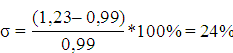
Находим частоту среза желаемой системы:

Исходя из частоты среза желаемой системы найдём её передедаточную функцию:

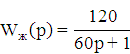
Разделив передаточную функцию желаемой системы на передаточную функцию исходной системы, получим передаточную функцию корректирующего устройства:

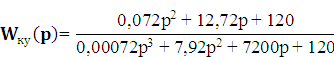
Рисунок 7 – Структурная схема

Строим ЛАЧХ желаемой системы (рисунок 7):

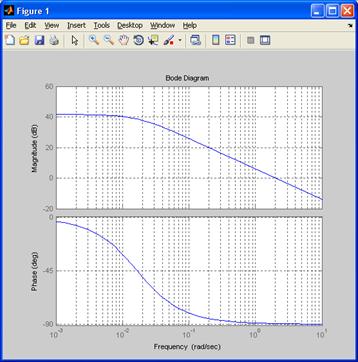
Рисунок 7 – ЛАЧХ желаемой системы

Определяем корни характеристического уравнения разомкнутой системы:

p₁ = - 0,0167.

Так как корни вещественные и отрицательные, то для устойчивой системы в замкнутом состоянии годограф Найквиста не должен охватывать точку с координатами [-1;j0].

Строим годограф Найквиста (рисунок 8):

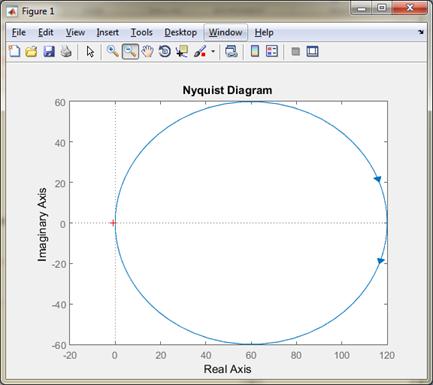
Рисунок 8 – Годограф Найквиста желаемой системы

Так как годограф Найквиста не охватывает точку с координатами [-1;j0], то АСУ устойчива.

Получим передаточную функцию (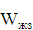) замкнутой системы:

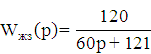
Строим переходный процесс в системе:

Рисунок 9 - Переходный процесс в замкнутой системе

Определяем показатели качества:

Максимальное динамическое отклонение, x_макс:

x_макс = 0

 

Время регулирования, t_р:

t_р = 3 с.

Перерегулирование, σ:

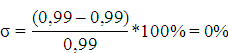
Получим передаточную функцию замкнутой дискретной системы:

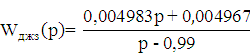
Строим переходный процесс в дискретной системе (рисунок 10):

Рисунок 10 - Переходный процесс в замкнутой дискретной системе

Показатели качества дискретной системы не отличаются от показателей качества аналоговой системы.