Державний вищий навчальний заклад
«Прикарпатський національний університет імені Василя Стефаника»
Кафедра математичного і функціонального аналізу
Курсова робота
на тему
«Особливі прийоми обчислення невласних інтегралів»
Студента IV курсу, групи М-42
Напряму підготовки «Математика»
Яневича Івана Васильовича
Керівник: Копач М.І.
Національна шкала:____________
Університетська шкала:_______
Оцінка ECTS:____
м. Івано-Франківськ – 2016 рік
Зміст
Вступ
1. Деякі чудові інтеграли.
2. Обчислення невласних інтегралів за допомогою інтегральних сум.
3. Інтеграли Фруллани.
4. Інтеграли від раціональних функцій.
5. Приклади.
Висновки.
Список використаної літератури.
Вступ
Невласні інтеграли є узагальненням визначених інтегралів на випадок нескінчених проміжків інтегрування та необмежених функцій.
Дана курсова робота містить основні відомості як обчислювати невласні інтеграли за допомогою інтегральних сум, інтеграли Фруллани, інтеграли від раціональних функцій, та деякі чудові інтеграли.
1. Деякі чудові інтеграли.
Почнемо з обчислення деяких важливих інтегралів за допомогою штучних прийомів. 1 °. Інтеграл Ейлера (L. Euler):
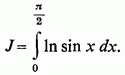
В його існування ми вже переконалися.
Обчислення інтеграла Ейлера засновано на використанні заміни змінної. Маємо,
вважаючи 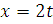

Підставляючи в останньому інтегралі
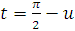 привидем
його до виду
привидем
його до виду 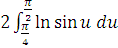 так
що, звичайно, для визначення J
отримуємо рівняння
так
що, звичайно, для визначення J
отримуємо рівняння

До цього ж інтеграла, з точністю до знака, наводяться і власні інтеграли
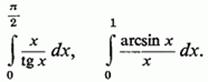
2 °. Звернемося до вирахування інтеграла Ейлера-Пуассона :
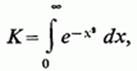
зустрічається в теорії ймовірностей. З цією метою попередньо встановимо деякі нерівності.
Звичайними в диференціальному численні
методами неважко встановити, що функція 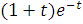 досягає
свого найбільшого значення 1 при
досягає
свого найбільшого значення 1 при 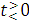 Отже,
для буде
Отже,
для буде
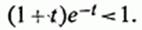
Вважаючи тут
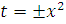 ми
отримаємо
ми
отримаємо

Звідки
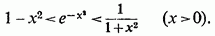
Обмеживши в першому з цих нерівностей
зміна х проміжком (0,1) (так
що 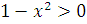 )
а в другому вважаючи x
будь-яким, піднесемо всі ці вирази в ступінь з будь-яким натуральним показником
це дає нам
)
а в другому вважаючи x
будь-яким, піднесемо всі ці вирази в ступінь з будь-яким натуральним показником
це дає нам
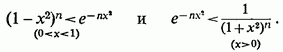
Інтегруючи першу нерівністьв проміжку
від 0 до 1, а другу - від 0 до +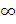
Отримаємо
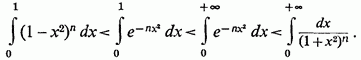
але
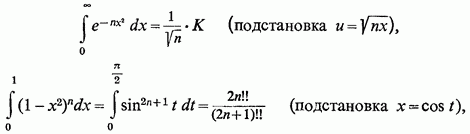
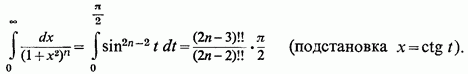
(Ми скористалися тут
відомими виразами для 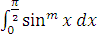
Таким чином, невідоме нам значення К може бути укладено між наступними двома виразами:
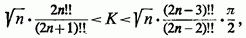
так що, зводячи в квадрат і перетворюючи, отримаємо
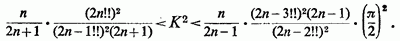
З формули Валліса :
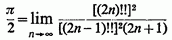
легко побачити тепер, що обидва крайніх
вирази при 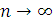 прямують
до однієї і тієї ж границі
прямують
до однієї і тієї ж границі  отже,
отже,
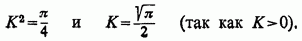
3 °. Розглянемо інтеграл
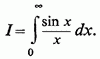
Ми знаємо, що він сходиться . Уявімо інтеграл у вигляді суми ряду

Поклавши 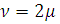 або
або
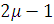 і
вдавшись, відповідно, до підстановки
і
вдавшись, відповідно, до підстановки 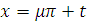 або
або
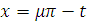 матимемо:
матимемо:
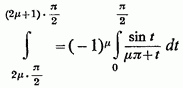
і
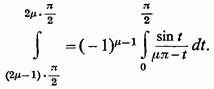
Звідси

Так як ряд
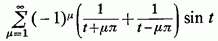
в проміжку 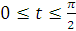 сходиться
рівномірно, fбо мажорується
збіжним рядом
сходиться
рівномірно, fбо мажорується
збіжним рядом 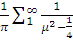 його можна інтегрувати почленно.
його можна інтегрувати почленно.
Це дає нам право написати вираз для I у вигляді:

Але вираз в квадратних дужках є розкладання на прості дроби функції. Таким чином, остаточно,
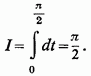
Наведений витончений висновок належить Лобачевському, який першим звернув увагу на нестрогість тих прийомів, за допомогою яких цей важливий інтеграл обчислювався раніше.
2.Обчислення невласних інтегралів за допомогою інтегральних сум
Якщо функція 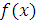 в
проміжку
в
проміжку 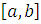 обмежена,
то довільними інтегральними (рімановими) сумами користуватися для обчислення її
інтегралів в цьому проміжку, зрозуміло, не можна. Однак завжди можна так
вибирати ці суми, щоб вони - при дробленні проміжку - прагнули до значення
невласного інтеграла. Ми встановимо це для найпростішого випадку монотонної
функції.
обмежена,
то довільними інтегральними (рімановими) сумами користуватися для обчислення її
інтегралів в цьому проміжку, зрозуміло, не можна. Однак завжди можна так
вибирати ці суми, щоб вони - при дробленні проміжку - прагнули до значення
невласного інтеграла. Ми встановимо це для найпростішого випадку монотонної
функції.
Отже, нехай функція
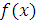 в
проміжку
в
проміжку 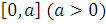 додатня,
монотонно спадає і при
додатня,
монотонно спадає і при 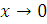 прямує
до
прямує
до 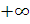 в
той же час, нехай для неї існує невласний інтеграл від 0 до
в
той же час, нехай для неї існує невласний інтеграл від 0 до 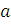 .
Розділивши проміжок
.
Розділивши проміжок 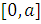 на
n рівних частин,
матимемо
на
n рівних частин,
матимемо
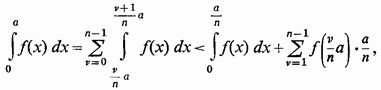
тим більше
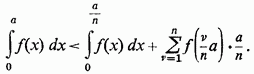
У той же час, очевидно,

так що, за сукупністю,
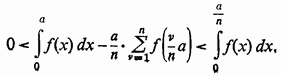
Так як останній інтеграл при 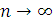 прямує
до нуля, то остаточно
прямує
до нуля, то остаточно
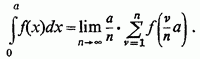
У разі додатньої зростаючої функції 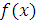 прямує
до
прямує
до 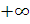 при
при
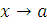 виходить
аналогічно
виходить
аналогічно
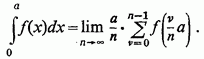
Нарешті, змінюючи знак 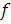 легко
отримати такі ж формули і для монотонної негативною функції.
легко
отримати такі ж формули і для монотонної негативною функції.
Розглянемо прикладb.
1) Для обчислення інтеграла 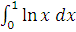 (з
особливою точкою 0) маємо:
(з
особливою точкою 0) маємо:
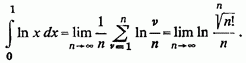
Так як 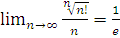 ,
то попередня границя дорівнює - 1; таке, насправді, і є значення
запропонованого інтеграла.
,
то попередня границя дорівнює - 1; таке, насправді, і є значення
запропонованого інтеграла.
2) В якості другого прикладу візьмемо
більш складний інтеграл: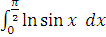
В цьому випадку
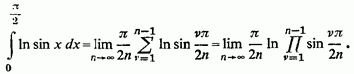
Бажаючи отримати просте вираження для
останнього , розглянемо цілий многочлен, що виходить від ділення
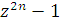 на
на
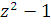 і
розкладемо його на лінійні множники, збираючи разом множники, які відповідають
спряженим
кореням.
Ми отримаємо (при будь-якому матеріальному z, відмінному
і
розкладемо його на лінійні множники, збираючи разом множники, які відповідають
спряженим
кореням.
Ми отримаємо (при будь-якому матеріальному z, відмінному 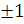 )
)
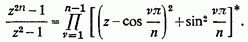
При 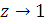 звідси
знайдемо:
звідси
знайдемо:
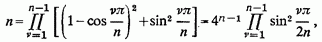
так що,

Тому шуканий інтеграл виявляється рівним:
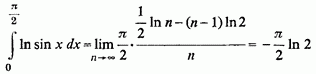
3.Інтеграли Фруллани
Розглянемо питання про існування і обчисленні одного приватного виду невласних інтегралів, зазвичай званих інтегралами Фруллані (G. Froullani):
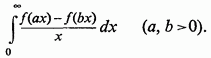
Щодо функції
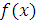 зробимо
наступні припущення: 1 °
зробимо
наступні припущення: 1 ° 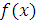 визначена
і неперервна для
визначена
і неперервна для 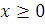 і
2 ° існує кінцевий межа
і
2 ° існує кінцевий межа
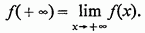
З 1 ° ясно, що існує (при
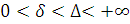 )інтеграл
)інтеграл
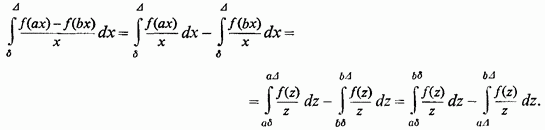
Запропонований же інтеграл визначається рівністю
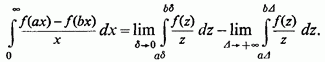
Застосовуючи до останніх двох интегралам порізно узагальнену теорему про середнє значення, отримаємо (де)
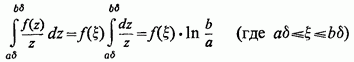
і, аналогічно,

Так як, очевидно,
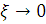 (при
(при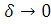 )
а
)
а
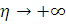 (при
(при 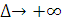 )
то звідси
)
то звідси
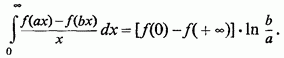
Приклади. 1) У випадку інтеграла
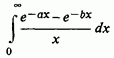
маємо:
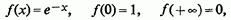
так що значення інтеграла буде 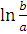
2) Нехай запропонований інтеграл
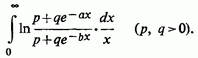
Замінюючи логарифми різницею логарифмів,
можна покласти тут 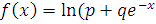 так
що
так
що 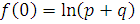 i
i
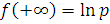 .
.
Відповідь.

3) Обчислити інтеграл

В цьому випадку
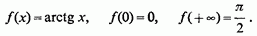
Відповідь.
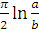
II. Інший раз функція
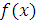 не
має кінцевої границі при
не
має кінцевої границі при 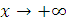 але
зате існує інтеграл
але
зате існує інтеграл
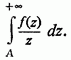
Замінюючи в наведеному міркуванні А
відразу на +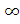 прийдемо,
натомість, до результату
прийдемо,
натомість, до результату
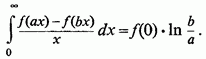
Приклад 4):
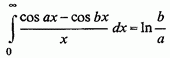
III. Аналогічно, якщо порушена
безперервність функції 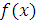 при
при
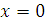 але
існує інтеграл
але
існує інтеграл
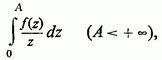
то
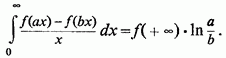
Втім, цей випадок наводиться до попереднього підстановкою

4.Інтеграли від раціональних функцій
На закінчення розглянемо ще один приватний тип інтеграла з нескінченними межами:

Де
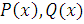 -
цілі
многочлени. Припустимо, що многочлен
-
цілі
многочлени. Припустимо, що многочлен 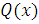 коренів не має і що стeпінь
коренів не має і що стeпінь 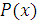 принаймні,
на дві одиниці нижче ступеня
принаймні,
на дві одиниці нижче ступеня 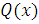 .
При цих умовах інтеграл існує питання лише в його обчисленні.
.
При цих умовах інтеграл існує питання лише в його обчисленні.
Якщо суть різні корені многочлена то дріб наступним чином розкладається на прості дроби

причому число дробів в кожної дужки дорівнює показнику кратності відповідного кореня.
Поширюючи на випадок комплексної функції від дійсної змінної елементарні способи обчислення інтегралів, бачимо відразу, що, при
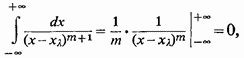
отже,
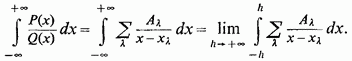
З іншого боку,

і
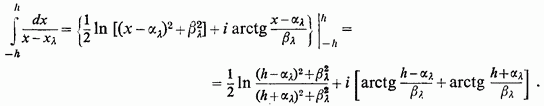
При
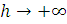 перший
доданок в останньому виразі прямує до 0, а друге до +
перший
доданок в останньому виразі прямує до 0, а друге до +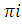 або
або
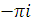 в
залежності від того, чи буде
в
залежності від того, чи буде 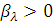 або
або
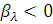
Таким чином, приходимо до результату:
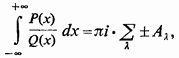
де
при 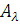 стоїть
знак плюс, якщо відповідне
стоїть
знак плюс, якщо відповідне 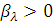 і
знак мінус в іншому випадку. Цю формулу можна дещо видозмінити на підставі
наступних міркувань. Помножимо обидві частини тотожності на х. При
і
знак мінус в іншому випадку. Цю формулу можна дещо видозмінити на підставі
наступних міркувань. Помножимо обидві частини тотожності на х. При
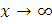 ліва
частина буде прямувати до 0, так як степінь
ліва
частина буде прямувати до 0, так як степінь 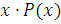 все
ж нижче стeпеня
все
ж нижче стeпеня 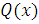 .
У правій частині в границі знищаться всі члени з нелінійними знаменниками, так
що і границя суми інших членів також 0. Звідси
.
У правій частині в границі знищаться всі члени з нелінійними знаменниками, так
що і границя суми інших членів також 0. Звідси 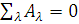 так,
що
так,
що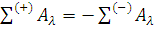 якщо знаком (+) і (
якщо знаком (+) і (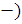 позначити
суми тих
позначити
суми тих 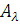 які
відповідають
які
відповідають 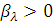 і
і 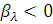 .Тепер
отриману формулу можна написати у вигляді
.Тепер
отриману формулу можна написати у вигляді

Що
стосується обчислення коефіцієнтів 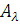 то
ми обмежимося вказівкою, що належать до випадку простого кореня
то
ми обмежимося вказівкою, що належать до випадку простого кореня
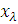 для
якого
для
якого 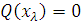 але
але
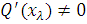 йому
відповідає в розкладанні (5) один тільки член
йому
відповідає в розкладанні (5) один тільки член
 .
Якщо обидві частини рівності (5) помножити на
.
Якщо обидві частини рівності (5) помножити на
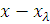 тo
воно представиться у вигляді
тo
воно представиться у вигляді
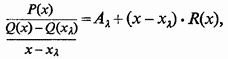
де
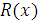 означає групу членів, які залишаються кінцевими при наближенні x
до
означає групу членів, які залишаються кінцевими при наближенні x
до
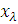 Переходячи до межі при
Переходячи до межі при 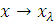 одержимо
одержимо
Звернемося тепер до прикладів застосування формул (6) і (7). 1) На першому місці розглянемо інтеграл
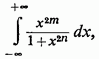
де - натуральні числа, причому Всі умови для застосування встановленої формули тут дотримані.
Корінням знаменника є числа
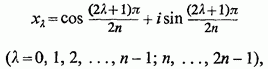
але лише перші і з них мають позитивні уявні частини. Очевидно, де
За формулою (7), при,
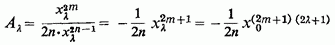
(З урахуванням того, що Підсумовуючи прогресію, отримуємо:
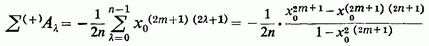
або, так як
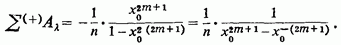
підставляючи
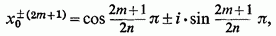
остаточно представимо потрібну нам суму у вигляді

Звідси ж, за формулою (6),
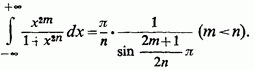
2) Кілька більш загальний приклад:

де - натуральні числа і
Умови виконані, за винятком того, що знаменник має речові коріння ± 1. Ця обставина тут не суттєво, бо ці коріння має і чисельник, так що дріб міг би бути скорочена на Надалі ці коріння не будемо брати до уваги.
Решта коріння знаменника суть

З них позитивні уявні частини мають перші По формулі (7)
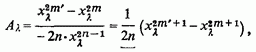
так що
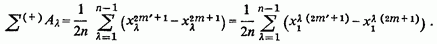
Отриманий вираз послідовно перетворюється так:
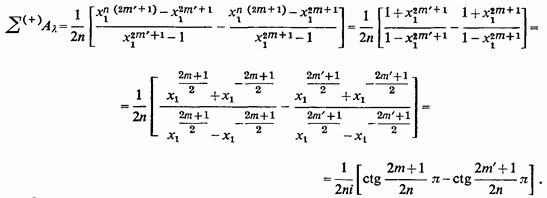
остаточно,
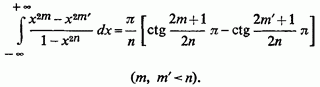
Зауважимо, що з цієї формули легко можна було б отримати і попередній результат, якщо замінити на і покласти
3) Нарешті, розглянемо інтеграл
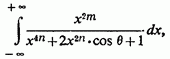
де
Вводячи кут перепишемо інтеграл так:
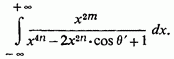
Для обчислення коренів знаменника покладемо тоді z визначиться з рівнянь саме,. Для х виходять дві серії значень
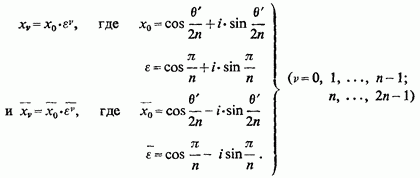
При цьому позитивну уявну частину матимуть перші з першої серії і останні з другої.
Відповідні коріння коефіцієнти обчислюються за формулою (7):

Підсумовуючи ці коефіцієнти і примножуючи на отримаємо
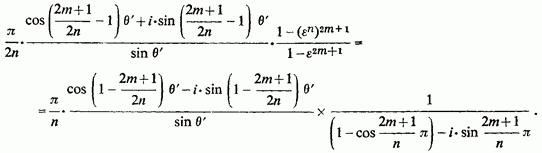
Для другої групи коренів аналогічно вийде вираз, поєднане з цим; їх сума дасть подвоєну речову частину. Після елементарних перетворень ця сума зведеться до

Повертаючись до кута остаточно отримаємо
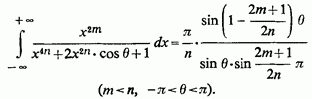
5.Приклади
1) Довести існування інтеграла
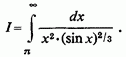
Особливих точок
безліч: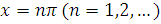 .
У будь-якому кінцевому проміжку їх кінцеве число, і інтеграл сходиться. Питання
лише про збіжність інтеграла в нескінченному проміжку.
.
У будь-якому кінцевому проміжку їх кінцеве число, і інтеграл сходиться. Питання
лише про збіжність інтеграла в нескінченному проміжку.
Маємо:

2) Якщо в збіжний інтеграл
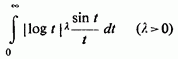
зробити
підстановку 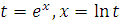 прийдемо
до інтеграла
прийдемо
до інтеграла

останній, таким чином, сходиться,
незважаючи на те, що підінтегральна функція при безмежному зростанні
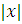 коливається між
коливається між 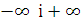
3) Ми бачили тільки що, що для збіжності інтеграла
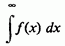 (1)
(1)
зовсім не потрібно навіть, щоб було
 (2)
(2)
Довести, що,
(а) якщо існує межа
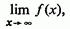
то - в разі збіжності інтеграла (1) ця межа дорівнює 0; більш того,
(б) якщо існує межа

то і ця межа дорівнює 0
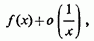 (3)
(3)
(в)
якщо інтегрована в проміжку 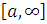 функція
монотонно спадає, то ця умова (3) необхідно виконується.
функція
монотонно спадає, то ця умова (3) необхідно виконується.
Доказ [для (б) і (в)] схоже з доказом аналогічних додатніх рядів.
Відзначимо ще (теж за аналогією з рядами), що навіть для монотонно спадної функції виконання умови (3) не гарантує збіжність інтеграла (1): прикладом може служити розбіжний інтеграл

Висновки
Дана курсова робота присвячена особливим прийомам обчислення невласних інтегралів.
У першому пункті наведено деякі чудові інтеграли.
У другому обчислення невласних інтегралів за допомогою інтегральних сум.
У третьму інтеграли Фруллани.
У четвертому інтеграли від ріціональних функцій.
Список використаної літератури
1. Г.М. Фихтенгольц Курс дифференциального и интегрального исчисления, том II М., Москва, 1969р - 800 с.
2. І.І. Ляшко, В.Ф. Ємельянов, О.К. Боярчук Математичний аналіз, Підручник: У 2 ч. Ч. I. Вища школа., 1992р . - 495 с.
3. М.І.Шкіль Математичний аналіз: Підручник. У 2ч. Ч І. – 2-ге вид., перероб. І допов. – К.: Вища школа., 1994 – 423 с.: іл.














 (zip - application/zip)
(zip - application/zip)










