Графические методы решения уравнений и неравенств 

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И МОЛОДЕЖНОЙ ПОЛИТИКИ                                      СТАВРОПОЛЬСКОГО КРАЯ

ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ПРОФЕССИОНАЛЬНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ «МНОГОПРОФИЛЬНЫЙ ТЕХНИКУМ ИМЕНИ КАЗАЧЬЕГО ГЕНЕРАЛА С.С.НИКОЛАЕВА»

                              Индивидуальный проект на тему:

            «Графические методы решения уравнений и неравенств» 

Выполнил Гончаров Артём Сергеевич

Руководитель Кравченко Светлана Владимировна

Михайловск, 2016

Содержание:

Введение. С.3

Возникновение и понятие функции в древнем мире. С.3

Возникновение и понятие функции в древнем Египте. С.4

Возникновение и понятие функции в Вавилоне. С.4

Графическое изображение зависимостей, а также история возникновения. С.5

Вклад в развитие графиков функций Рене Декарта. С.6

Графическое решение линейных уравнений. С.7

Алгоритм построения графика функций. С.8

Заключение. С.13

Список источников. С.15

Цель.

I.Узнать, как решаются графические методы решения уравнений и неравенств.

II.Рассмотреть разные  способы решений уравнений и неравенств.

Введение.

    Изучение поведения функций и построение их графиков является важным разделом математики. Свободное владение техникой построения графиков часто помогает решить многие задачи и парой является единственным средством их решения. Кроме того, умение строить графики функций представляет большой самостоятельный интерес.

Возникновение и понятие функции в древнем мире.

    Понятие функции уходит своими корнями в ту далекую эпоху, когда люди впервые поняли, что окружающие их явления взаимосвязаны. Они еще не умели считать, но уже знали, что, чем больше оленей удастся убить на охоте, тем дольше племя будет избавлено от голода, чем дольше горит костер, тем теплее будет в пещере.

    С развитием скотоводства и земледелия, ремесла и обмена увеличилось количество известных людям зависимостей между величинами. Многие из них выражались с помощью чисел. Это позволило формулировать их словами "больше на", "меньше на", "больше во столько-то раз". Если за одного быка давали 6 овец, то двух быков обменивали на 12 овец, а трех быков на 18 овец. Такие расчеты привели к возникновению понятия о пропорциональности величин.

Возникновение и понятие функции в древнем Египте.

    Но когда возникли первые цивилизации, образовались большие (по тогдашним масштабам), армии, началось строительство гигантских пирамид, то понадобились писцы, которые учитывали поступающие налоги, определяли количество кирпичей, потребное для возведения дворцов, подсчитывали, сколько продовольствия надо заготовить для дальних походов. От одного поколения писцов к другому переходили правила решения задач, чтобы решить такие задачи, надо было знать, как зависят объемы геометрических фигур от их размеров, уметь учитывать наклон насыпи. Некоторые египетские задачи показывают, что в то время умели даже вычислить объем пирамиды

Возникновение и понятие функции в Вавилоне.

 Высокого уровня достигла математика в Древнем Вавилоне. Чтобы облегчить вычисления, вавилоняне составили таблицы обратных значений чисел, таблицы квадратов и кубов чисел и даже таблицы для суммы квадратов чисел их кубов. Говоря современным языком, это было табличное задание функций y = 1/x, y = 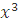, y = , y =  + .

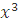    Пользуясь такими таблицами, вавилоняне могли решать и обратные задачи - по заданному объему куба находить длину его стороны, т.е. извлекать кубические корни. Они умели даже решать уравнения вида  +  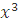= a. Были у вавилонян и таблицы функций двух переменных, например, таблицы сложения и умножения. Пользуясь различными таблицами, они могли вычислить и длину гипотенузы по длинам катетов, т.е. находить значение функции. 

    Разумеется, путь от появления таблиц до создания общего понятия функциональной зависимости был еще очень долог, но первые шаги по этому пути уже были сделаны.

Графическое изображение зависимостей, а также история возникновения.

    Исследование общих зависимостей началось в 14 веке. Средневековая наука была схоластической. Для доказательства своей правоты ученые прибегли не к опыту, а к цитатам из Аристотеля и Платона или к ссылкам на библейские сказания. При таком характере "научных дискуссий" не оставалось места изучению количественных зависимостей, речь шла лишь о качествах предметов и их связях друг с другом. Но среди схоластов возникла школа, утверждавшая, что качества могут быть более или менее интенсивными (платье человека, свалившегося в реку, мокрее, чем у того, кто лишь попал под дождь).

    Французский ученый Николай Оресм стал изображать интенсивность длинами отрезков. Когда он располагал эти отрезки перпендикулярно некоторой прямой, их концы образовывали линию, названную им "линией интенсивностей" или "линией верхнего края". Современный читатель сразу узнает в ней график соответствующей функциональной зависимости. Оресм изучал даже "плоскостные" и "телесные" качества, т.е. функции, зависящие от двух или трех переменных.

    Важным достижением Оресма была попытка классифицировать получившиеся графики. Он выделил три типа качеств: равномерные (с постоянной интенсивностью), равномерно-неравномерные (с постоянной скоростью изменения интенсивности) и неравномерно-неравномерные (все остальные), а также характерные свойства графиков таких качеств.

    Идеи Оресма на много обогнали тогдашний уровень науки. Чтобы развивать их дальше, нужно было уметь выражать зависимости между величинами не только графически, но и с помощью формул, а буквенной, алгебры в то время не существовало. Лишь после того, как в течение 16 века была постепенно создана буквенная алгебра, удалось сделать следующий шаг в развитии понятия функции.

Вклад в развитие графиков функций Рене Декарта.

    Чтобы создать математический аппарат для изучения графиков функций, понадобилось понятие переменной величины. Это понятие было введено в науку французским философом и математиком Рене Декартом (1596-1650). Именно Декарт пришел к идеям о единстве алгебры и геометрии и о роли переменных величин, он разрушил пропасть, лежавшую со времен древнегреческой математики, между геометрией и арифметикой.

    Чтобы освободить алгебру от несвойственного ей геометрического языка, Декарт ввел фиксированный единичный отрезок и стал рассматривать отношения других отрезков к нему.

    При записи зависимостей между величинами Декарт стал применять буквы. При этом операциями над величинами соответствовали операции над буквами. Теперь уже для преобразования одной зависимости в другую не надо было писать громоздких пропорций, изучать подобные треугольники и преобразовывать геометрические фигуры. Достаточно было по твердо, установленным правилам делать алгебраические преобразования, причем все эти преобразования производились в общем виде.

Таким образом, графики функций за все время своего существования прошли через ряд фундаментальных преобразований, приведших их к тому виду, к которому мы привыкли. Каждый этап или ступень развития графиков функций - неотъемлемая часть истории современной алгебры и геометрии.

График является опорным образом при усвоении значительного числа функциональных понятий. Идея функциональной зависимости, формируемая в курсе алгебры, является основополагающей для понимания реальных процессов и явлений, рассматриваемых в смежных дисциплинах.

    Так, например, при изучении равноускоренного движения используется сведения о линейной функции, при изучении электричества – сведения о прямой и обратной пропорциональности.

    При введении координат и векторов целесообразно использовать сведения о графическом изображении сил.

    Ноты – распространённый способ письменной шифровки мелодии. Однако в последнее время потребовалось научиться кодировать мелодию и другими способами (понотным и потактным введением координатной метрической сетки, графически).

Графическое решение линейных уравнений.

При построении графиков и решении уравнений используются свойства функции, поэтому метод чаще называют функционально-графическим.

Для решения уравнение «делим» на две части, вводим две функции, строим их графики, находим координаты точек пересечения графиков. Абсциссы этих точек и есть корни уравнения.

Алгоритм построения графика функции.

Зная график функции у = f(x), можно построить графики функций у = f(x+m), у = f(x)+l и у = f(x+ m)+ l.

Все эти графики получаются из графика функции у = f(x) с помощью преобразования параллельного переноса: на│m│ единиц масштаба вправо или влево вдоль оси x и на│l│ единиц масштаба вверх или вниз вдоль оси y.

Графиком линейного уравнения является прямая линия, отсюда и название данного вида. Линейные уравнения достаточно легко решать алгебраическим путем – все неизвестные переносим в одну сторону уравнения, а все известные – в другую. Так находится корень.

Гра­фи­че­ски ре­шить урав­не­ние: 

Ре­ше­ние:

По­стро­им гра­фи­ки функ­ций .

Гра­фи­ком функ­ции  яв­ля­ет­ся па­ра­бо­ла, про­хо­дя­щая через точки 

Гра­фик функ­ции  – пря­мая, по­стро­им её по таб­ли­це.

	0
	3	0

Гра­фи­ки пе­ре­се­ка­ют­ся в точке   Дру­гих точек пе­ре­се­че­ния нет, т.к. функ­ция  мо­но­тон­но воз­рас­та­ет, функ­ция  мо­но­тон­но убы­ва­ет, а, зна­чит, их точка пе­ре­се­че­ния яв­ля­ет­ся един­ствен­ной.

Ответ: 

Графически решить квадратное   уравнение

    – 2x – 3 = 0  

 перенесем все слагаемые, кроме    в правую часть уравнения 

=   2x + 3;

 введем переменную   y:

   =   y   =   2x + 3;

построим графики полученных функций. 

   Точки пересечения прямой   y = 2x+3   c параболой    y =   

имеют координаты (–1; 1) и (3; 9).

Абсциссы этих точек являются решением нашего квадратного уравнения:  

x 1 = –1, x 2 = 3. 

Проверим, подставив полученные решения в уравнение    – 2x – 3 = 0. 

(−1) 2 – 2 • (−1) – 3 = 0     ⇒   1 + 2 – 3 = 0   — верное числовое равенство. 

3 • 3 – 2 • 3 – 3 = 0     ⇒   9 – 6 – 3 = 0   — верное числовое равенство.   

          Значит, уравнение     – 2x – 3 = 0   имеет два решения:   

x 1   =   –1 ,           x 2   =   3 .

Ре­шить нера­вен­ство.

a. 

b. 

Ре­ше­ние:

a. Чтобы вы­пол­ня­лось нера­вен­ство, гра­фик функ­ции  дол­жен рас­по­ла­гать­ся над пря­мой  (Рис. 1). Это вы­пол­ня­ет­ся при 

b. В этом слу­чае, на­о­бо­рот, па­ра­бо­ла  долж­на на­хо­дить­ся под пря­мой. Это вы­пол­ня­ет­ся при 

a. 

b. 

Ре­шить нера­вен­ство

 

Ре­ше­ние:

По­стро­им гра­фи­ки функ­ций .

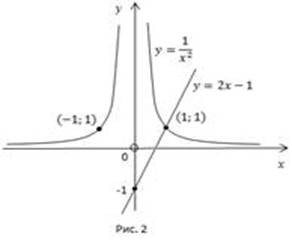
Най­дем ко­рень урав­не­ния  

При  нет ре­ше­ний.

При  су­ще­ству­ет одно ре­ше­ние  .

Чтобы вы­пол­ня­лось нера­вен­ство  ги­пер­бо­ла  долж­на рас­по­ла­гать­ся над пря­мой  

Это вы­пол­ня­ет­ся при .

Ответ: 

Ре­шить гра­фи­че­ски нера­вен­ство:

a. 

b. 

Ре­ше­ние.

Об­ласть опре­де­ле­ния: 

По­стро­им гра­фи­ки функ­ций 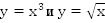 для  (Рис. 3).

a. Гра­фик функ­ции  дол­жен рас­по­ла­гать­ся под гра­фи­ком  это вы­пол­ня­ет­ся при 

b. Гра­фик функ­ции  рас­по­ло­жен над гра­фи­ком  при  Но т.к. в усло­вии имеем нестро­гий знак, важно не по­те­рять изо­ли­ро­ван­ный ко­рень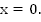 

Ответ:

a. 

b. 

Заключение.

Графические способы решения уравнений красивы и понятны, но не дают стопроцентной гарантии решения любого уравнения. Абсциссы точек пересечения графиков могут быть приближёнными.

Математика - удивительная наука. При всей своей искусственности она умудряется описывать каждый процесс, происходящий с нами и вокруг нас.

Она всегда направлена на некий результат или же на доказательство того, что результата добиться невозможно. Иными словами, все в математике подчинено алгоритмам. Алгоритм - это заданная последовательность действий, направленная на достижение определенной цели. Похоже на работу, не так ли? Цели одни и те же.

Любая человеческая деятельность, какой бы творческой и абстрактной она ни была, в основе своей содержит самое простое - механизм действия. То, что можно описать и разложить пошагово на математические формулы. Математика - скелет любого процесса.

Математика в профессии повара.

 Не стоит недооценивать эту профессию. Повар - это не просто человек, который может быстро сделать суши или пельмени (в зависимости от запроса). Он творец, способный из кучки самых простых продуктов создать шедевр, при этом учтя все погрешности и характер изменения пищи в процессе термообработки.

Итак, некоторые из его обязанностей:

·            Калькуляция блюда. Проще говоря, расписанный до грамма рецепт. Привычный метод "на глазок" в подобных случаях не действует: все позиции задокументированы и заверены. Это необходимо для ведения финансовой части точки общепита.

·            Учет потери веса продуктов в процессе обработки. Например, 250 грамм говядины и 250 грамм готового стейка - это разные вещи, так как при обжарке мясо теряет процент веса. Причем в зависимости от влажности продукта и срока/вида термообработки потеря веса меняется. Таким образом, математика в профессии повара играет первую скрипку наравне с практическими умениями.

·            Подсчет продуктов и порций, необходимых для банкета, в зависимости от того, какое количество гостей планируется. Данное число должно включать в себя все риски и погрешности, дабы посередине мероприятия не возникло неприятных сюрпризов. Вывод пропорций, основанный на сиюминутных потребностях заведения. Исходит из таких показателей, как количество посадочных мест, предполагаемая интенсивность посещаемости плюс небольшой форс-мажор. Все это направлено на то, чтобы избежать или минимизировать порчу продуктов, закупаемых ежедневно. Ведь рыба бывает лишь первой свежести, по версии Булгакова.

Задаваясь вопросом, какую роль играет математика в нашей будущей профессии, мы должны понимать, что она будет везде, куда бы мы ни ступили. Самостоятельно или же в симбиозе с другими науками она образует фундамент для новых свершений.

 Спи­сок источников:

1. Морд­ко­вич А.Г. и др. Ал­геб­ра 9 кл.: Учеб. Для об­ще­об­ра­зо­ват. Учре­жде­ний.- 4-е изд. – М.: Мне­мо­зи­на, 2002.-192 с.: ил.

2. Морд­ко­вич А.Г. и др. Ал­геб­ра 9 кл.: За­дач­ник для уча­щих­ся об­ще­об­ра­зо­ва­тель­ных учре­жде­ний / А. Г. Морд­ко­вич, Т. Н. Ми­шу­ст­и­на и др. — 4-е изд. — М.: Мне­мо­зи­на, 2002.-143 с.: ил.

3. Ма­ка­ры­чев Ю. Н. Ал­геб­ра. 9 класс : учеб. для уча­щих­ся об­ще­об­ра­зо­ват. учре­жде­ний / Ю. Н. Ма­ка­ры­чев, Н. Г. Мин­дюк, К. И. Неш­ков, И. Е. Фео­к­ти­стов. — 7-е изд., испр. и доп. — М.: Мне­мо­зи­на, 2008.

4. Али­мов Ш.А., Ко­ля­гин Ю.М., Си­до­ров Ю.В. Ал­геб­ра. 9 класс. 16-е изд. - М., 2011. - 287 с.

5. Морд­ко­вич А. Г. Ал­геб­ра. 9 класс. В 2 ч. Ч. 1. Учеб­ник для уча­щих­ся об­ще­об­ра­зо­ва­тель­ных учре­жде­ний / А. Г. Морд­ко­вич, П. В. Се­ме­нов. — 12-е изд., стер. — М.: 2010. — 224 с.: ил.

6. Ал­геб­ра. 9 класс. В 2 ч. Ч. 2. За­дач­ник для уча­щих­ся об­ще­об­ра­зо­ва­тель­ных учре­жде­ний / А. Г. Морд­ко­вич, Л. А. Алек­сан­дро­ва, Т. Н. Ми­шу­ст­и­на и др.; Под ред. А. Г. Морд­ко­ви­ча. — 12-е изд., испр. — М.: 2010.-223 с.: ил.

Список ссыл­ок на Интернет-ресурсы

1. Раз­дел College. ​ru по ма­те­ма­ти­ке (Ис­точ­ник).

2. Ин­тер­нет-про­ект «За­да­чи» (Ис­точ­ник).

3. Об­ра­зо­ва­тель­ный пор­тал «РЕШУ ЕГЭ» (Ис­точ­ник).