Механизмы привода глубинного насоса

Министерство образования и науки Украины

Сумский государственный университет

Механизмы привода глубинного

насоса

ПОЯСНИТЕЛЬНАЯ ЗАПИСКА

к курсовому проекту по теории механизмов и машин

МПГН 07.05.00 ПЗ

Руководитель проекта                                                     _______________

Выполнил студент                                                             _______________

Группа                                                                                   _______________

Сумы – 2016

Содержание

ЗАДАНИЕ……………………………………………………………………………………………………......3

ВВЕДЕНИЕ……………………………………………………………………………………………………5

ЦЕЛЬ КУРСОГО ПРОЕКТА…………………………………………………………………………….6

1.1  Построенте плана механизма

План механизма строим, для двенадцати положений. Построение начнём с выбора длины отрезка кривошипа (45 мм), обозначим через АO  длину отрезка шатуна в миллиметрах, а через I_АО – истинную длину кривошипа в метрах, составив отношение истинной длины к длине отрезка получим значение масштабного коэффициента.

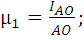                                                                                            (1,1)

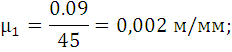
По значению µ₁ находим длины отрезков остальных  звеньев  механизма  в миллиметрах. Для этого истинные длины звеньев в метрах делим на масштаб µ₁.

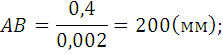
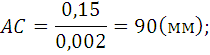
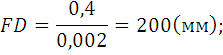
Отрезком ОА, как радиусом, изображаем окружность с центром в точке О₁

С учетом масштаба µ₁ на чертеже находим геометрические  места  неподвижных осей вращения F и E, направляющих для ползунов.

Путем вращения ОА отрезка находим два крайних (мертвых)  положения механизма.

После нахождения мертвых положений механизма и определения направления вращения кривошипа строим план механизма.

За исходное нулевое выбираем первое мертвое положение механизма. Последующие положения строим через 30° поворота кривошипа.

1.2 Построение плана аналогов скоростей

Определим скорость точки А. Зная частоту вращения кривошипа ОА и его

длину, определим скорость точки А, используя формулу:

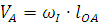                                                                                                                     (1.2)

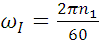                                                                                               (1.3)

где n₁ – частота вращения кривошипа.

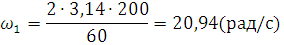
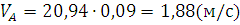
Скорость точки А во всех положениях механизма постоянна, и графически выражается вектором ра.

Определим масштабный коэффициент плана скоростей.

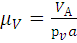                                                                                                                  (1.4)

где ра – отрезок на плане скоростей определяющий скорость точки А, мм.

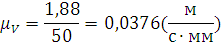
Определяем скорость точки В. Для этого рассмотрим её движение относительно точки А. Получаем уравнение:

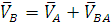                                                                                                        (1.5)

где: V_B – скорость точки В;

         V_BA – скорость точки В относительно точки А;

Решая графическим методом систему уравнений (1.5), получим скорость точки В, которая графически выражается вектором pb.

Для определения скорости точки С₅, проведём прямую перпендикулярную отрезку FD и проходящую через полюс P_V . Далее соединим отрезком полюс P_V и отрезок ab по направлению прямой. На пересечении получим скорость точки С₅ , которая графически выражается вектором pc₅.

Скорость точки C₂ находим по принципу подобия. Берём отрезок AB с плана механизма, условно совмещаем точку B с точкой b, а точку, A с точкой a. Находим  положение  точки  c₂,  соответствующей  точке  C₂  на  продолжении  отрезка  ab. Длину отрезка ac₂ определяем из пропорции:

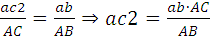                                                                                  (1.7)

Аналогично находим скорость точки D:

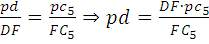                                                                                  (1.8)