АСТРАХАНСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

 

Кафедра: Электротехники, электроники и автоматики

Реферат

По теме: «Цифровые измерительные приборы»

                                                                                
            Выполнил:

 студент 3-го курса, гр. РТ-31

                   Гусейханов Ф. Ш.

         Проверил:

                                                                                     кандидат технических наук,                доцент кафедры прикладной

математики, информатики

и управления качеством

Абзалов А. В.

г. Астрахань, 2016 г.

Оглавление

1. ПРИНЦИПЫ ПОСТРОЕНИЯ И ОСНОВНЫЕ ТЕХНИЧЕСКИЕ ХАРАКТЕРИСТИКИ ЦИФРОВЫХ ИЗМЕРИТЕЛЬНЫХ ПРИБОРОВ.. 2

2. СТРУКТУРНАЯ СХЕМА ЦИФРОВОГО ИЗМЕРИТЕЛЬНОГО ПРИБОРА.. 6

3. СРАВНИТЕЛЬНАЯ ХАРАКТЕРИСТИКА АНАЛОГОВЫХ И ЦИФРОВЫХ ПРИБОРОВ   7

4. СПИСОК ЛИТЕРАТУРЫ... 9

 

1. ПРИНЦИПЫ ПОСТРОЕНИЯ И ОСНОВНЫЕ ТЕХНИЧЕСКИЕ ХАРАКТЕРИСТИКИ ЦИФРОВЫХ ИЗМЕРИТЕЛЬНЫХ ПРИБОРОВ

Цифровой измерительный прибор (ЦИП) — средство измерений, автоматически вырабатывающее сигналы измерительной информации в цифровой форме. Цифровой измерительный прибор имеет ряд преи­муществ перед аналоговыми приборами: удобство отсчитывания зна­чений измеряемой величины, возможность полной автоматизации про­цесса измерений, регистрация результатов измерения с помощью цифропечатающих устройств и перфораторов. Поскольку результат измере­ния в ЦИП выражен в цифровом коде, измерительную информацию можно вводить в цифровую ЭВМ.

В ЦИП происходит преобразование непрерывной измеряемой вели­чины в цифровой код. Осуществляется этот процесс с помощью ана­лого-цифрового преобразователя (АЦП), в котором сигнал измеритель­ной информации подвергается дискретизации, квантованию и кодиро­ванию.

Дискретизация, т. е. процесс преобразования непрерывного сигна­ла измерительной информации в дискретный, может осуществляться как по времени, так и по уровню. Дискретизация по времени выпол­няется путем взятия отсчетов сигнала X(t) в определенные детермини­рованные моменты времени. Таким образом, от сигнала измеритель­ной информации сохраняется только совокупность отдельных значе­ний. Промежуток времени между двумя моментами дискретизации называют шагом дискретизации. Обычно моменты отсчетов на оси времени выбираются равномерно, т. е. шаг дискретизации по­стоянен.

Дискретизация значений измерительного сигнала по уровню но­сит название квантования. Операция квантования сводится к тому, что непрерывная по времени и амплитуде величина заменяется бли­жайшим фиксированным значением по установленной шкале дискрет­ных уровней. Эти дискретные (разрешенные) уровни образованы по оп­ределенному закону с помощью мер. Разность ∆X между двумя раз­решенными уровнями называют интервалом (шагом или ступенью) квантования. Интервал квантования может быть как постоянным, так и переменным. Временная дискретизация измерительного сигнала имеет смысл, когда его величина изменяется во времени. Если измери­тельный сигнал постоянен, достаточно осуществить квантование. Осо­бым случаем является измерение времени (временного интервала). Процесс дискретизации здесь теряет смысл, и осуществляется кванто­вание самого времени.

Следующим преобразованием измерительного сигнала, является кодирование. Цифровым кодом называется последовательность цифр или сигналов, подчиняющаяся определенному закону, с помощью ко­торой осуществляется ус­ловное представление чис­ленного значения величи­ны. Графически описан­ные преобразования пояс­няются на рис.1 Исход­ный измерительный сигнал X(t) (рис.1,а) представ­ляет собой непрерывную функцию времени. Дискре­тизация выполняется с ин­тервалом 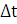. Моменты ди­скретизации отмечены на рис.1,а цифрами 1…9. Практически такую дискретизацию можно осу­ществить путем амплитуд­ной модуляции исходным сигналом X(t) последова­тельности коротких им­пульсов с периодом ∆t. Как видно из рис.1,б значе­ния сигнала X(t) полу­ченные после дискретиза­ции, точно соответствуют мгновенным значениям функции X(t). Если на том же рисунке отметить уровни квантования, рас­положенные друг от друга на расстоянии ∆X, то часть дискретных значений сигнала окажется в проме­жутках между ними. Про­цесс квантования по уровню сводится к округлению дискретных значений сигнала до значений, соответствующих ближайшим разре­шенным уровням. Так, в момент 1 мгновенное значение сигнала превышает уровень Х₃ на величину, несколько меньшую ∆X/2 (рис. 1.1, б). Округление производится в сторону уменьшения, и кван­тованное значение выбирается равным Х₃ . В момент 2 значение сиг­нала превышает уровень Х₄ на величину, большую чем ∆X/2. Квантованное значение принимается равным Х₅ (рис.1,в). Последний этап заключается в преобразовании квантованного сигнала X(t_i)_кв в цифровой код. На рис.1,г представлен для примера цифровой унитарный код X(t_i)_код, соответствующий значениям квантованного сигнала. При таком способе кодирования число импульсов в кодовой группе прямо пропорционально уровню квантованного сигнала. На­пример, отсчету 7 соответствует уровень квантования Х₆, и в кодо­вой группе n₇ содержится шесть импульсов.

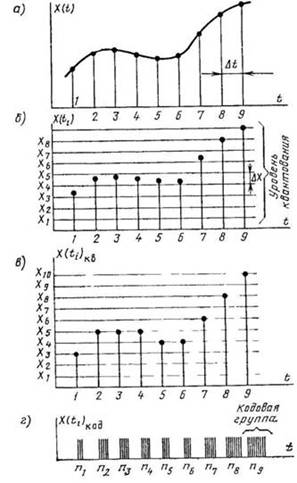
Рис. 1

Из рис.1 ясно, что при дискретизации и квантовании сигнала возникает погрешность преобразования. Непрерывная функция X(t) анализируется только в моменты дискретизации. На интервале 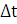 меж­ду двумя отсчетными точками сигнал предполагается неизменным. Уменьшением интервала 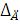,    т. е. сближением отсчетных точек можно добиться снижения погрешности до допустимой величины. При изме­рении постоянных величин погрешность преобразования, связанная с дискретизацией, равна нулю. Погрешность, возникающая при кван­товании непрерывной измеряемой величины, обусловлена конечным числом уровней квантования. Эта погрешность характерна для всех ЦИП, она носит название погрешности дискретности 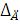. При равно­мерном квантовании погрешность 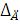 находится в пределах          .

Следующий этап преобразований в ЦИП заключается в превраще­нии цифрового кода в показания цифрового отсчетного устройства. Для этого необходим дешифратор, который превращает кодовые груп­пы в соответствующие напряжения, управляющие работой цифрового индикатора.

Рассмотренная последовательность преобразований, осуществляе­мая в аналого-цифровом преобразователе (АЦП), дешифраторе и циф­ровом индикаторе, конечно дает упрощенное представление о работе ЦИП. Примером может служить случай измерения постоянной вели­чины. Для этого достаточно одного цикла преобразований, в резуль­тате которого получится кодовая группа. Но кодовая группа это «па­кет» импульсов, передаваемый в течение короткого интервала време­ни. Результат измерений должен сохраняться на экране достаточно долго, например до следующего цикла. Поэтому в состав ЦИП долж­но входить запоминающее устройство (ЗУ).

Пере­числим возможные режимы работы ЦИП и их характеристики.

Режим однократного измерения. Этот режим удобен, когда изме­ряемый параметр постоянен. Команда на проведение измерения подает­ся оператором, результат измерения хранится в запоминающем уст­ройстве и воспроизводится на цифровом индикаторе. В ЦИП осуще­ствляется квантование измерительного сигнала и его кодирование.

Режим периодического измерения. Процесс измерения повторяет­ся периодически через интервал 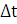, установленный оператором. В ЦИП осуществляются операции дискретизации, квантования и коди­рования. После каждого цикла измерения результат на экране циф­рового индикатора обновляется.

Следящий режим измерения. Цикл измерения повторяется, после того как изменение измеряемой величины превысит ступень кванто­вания.

Помимо погрешности измерения, к числу важных характеристик ЦИП относится его быстродействие, время измерения и помехоустой­чивость. Под быстродействием ЦИП понимается максимальное число измерений, выполняемых в единицу времени с нормированной погреш­ностью. Время измерения — интервал от начала цикла преобразова­ния измеряемой величины до получения результата. Под помехоустой­чивостью понимают способность ЦИП с нормированной погрешностью производить измерения при наличии помех.

Быстродействие ЦИП очень высокое. Современная элементная база позволяет строить ЦИП, обеспечивающие до 10⁷ преобразований в секунду. Это, однако, оказывается излишним, поскольку регистри­рующие устройства обеспечивают фиксацию не более 100 результатов измерений в секунду. При визуальном наблюдении требования к быст­родействию резко снижаются, поскольку оператор способен оценить не более 2—3 результатов измерений в секунду.

Основные технические характеристики ЦИП:

1)    номинальная статическая характеристика преобразования;

2)    диапазон измерений;

3)    вид кода, применяемого в АЦП, количество разрядов, вес единицы младшего разряда кода;

4)    разрешающая способность, характеризующаяся количеством уровней квантования;

5)    входное сопротивление;

6)    быстродействие;

7)    помехоустойчивость – способность ЦИП выполнять свои функции в условиях воздействия помех, численно характеризуется коэффициентом подавления помех на входе ИП;

8)    время измерения – интервал времени от момента начала цикла преобразования измеряемой физической величины до момента высвечивания показания на табло;

9)    погрешности. Нормируются 4 основных составляющих погрешности:

·        погрешность дискретизации;

·        погрешность реализации уровней квантования;

·        погрешность сравнения;

·        погрешность от воздействия помех.

Первая относится к методическим погрешностям, остальные – к инструментальным и обусловлены технической реализацией ИП;

10)          класс точности. Обычно в ЦИП для установления класса точности   нормируется относительная погрешность, рассчитываемая по так называемой «двухчленной формуле»:

,

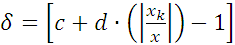где 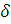 - относительная погрешность;

 - числа, выбираемые из того же ряда, что и класс точности;

 - конечное значение установленного предела излучения;

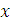 - измеряемое значение ФВ.

Класс точности обозначается .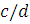

2. СТРУКТУРНАЯ СХЕМА ЦИФРОВОГО ИЗМЕРИТЕЛЬНОГО ПРИБОРА

Рис. 2 Структурная схема ЦИП

Измерительная величина u_x поступает на входное устройство прибора где происходит преобразование сигнала, затем он поступает на аналогово-цифровой преобразователь (АЦП) где аналоговый сигнал преобразуется в соответствующий код в виде цифр на цифровом отсчётном устройстве. В цифровом измерительном приборе предусмотрено управляющее устройство для получения управляющих сигналов. 

 

 

 

 

 

 

 

 

 

 

3. СРАВНИТЕЛЬНАЯ ХАРАКТЕРИСТИКА АНАЛОГОВЫХ И ЦИФРОВЫХ ПРИБОРОВ

Не следует считать, что ЦИП в будущем полностью вытес­няет аналоговые приборы. Аналоговые приборы просты и надежны. В тех случаях, когда оператору необходимо следить за уровнями из­меняющихся во времени сигналов, стрелочные указатели более удобны из-за наглядности представления об изменениях величины, о ее мини­мальном значении, приближении к порогу и т. п.

По результатам, полученным на основе опыта производства и эксплуатации аналоговых и цифровых приборов, можно обобщенно сравнить аналоговые и цифровые приборы в координатах «точность» и «быстродействие», «стоимость» и «сложность».

Каждый аналоговый и цифровой прибор можно изобразить одной точкой на плоскости в координатах «точность» и «быстродействие», а затем полосы, заполненные точками, сжать в обобщенные кривые, представленные на рис. 3.1.

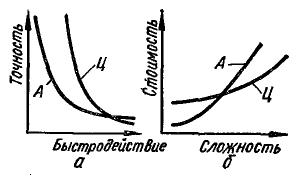
Рис. 3 Сравнение аналоговых и цифровых измерительных устройств

На основе полученных зависимостей можно сделать следующие выводы. В области средней и высокой точности цифровые приборы имеют значительно более высокое быстродействие, чем аналоговые, а в области наиболее высокого быстродействия более высокую точность имеют аналоговые приборы (рис.3,а). Большая часть цифровых приборов имеет высокое быстродействие, но их возможная точность в этой области резко уменьшается, так как дальнейшее увеличение быстродействия после использования самых быстродействующих ключей возможно путем уменьшения числа ступеней квантования по значению, т.е. снижением точности. Точность аналоговых приборов с повышением быстродействия также уменьшается, но с определенного значения более медленно, чем у цифровых. Это объясняется использованием в аналоговых приборах с наиболее высоким быстродействием в качестве выходной величины перемещения почти безынерционного луча.

Если аналогичное изображение совокупности всех цифровых и аналоговых измерительных приборов представить в координатах стоимости прибора и сложности решаемой измерительной задачи, то получим кривые, представленные на рис.3,б. Анализируя их можно прийти к следующим выводам:

1)    менее сложные измерительные задачи с меньшими затратами решаются аналоговыми приборами;

2)    более сложные измерительные задачи, например задачи измерительно-информационных систем, обрабатывающих результаты измерения по сложной программе, с меньшими затратами решаются автоматически цифровыми измерительными устройствами;

3)    при повышении быстродействия элементов цифровых приборов точка пересечения кривых в координатах «точность» и «быстродействие» сдвигается вправо, расширяя зону, в которой более совершенны цифровые приборы;

4)    применение микропроцессоров, позволяющее уменьшить число корпусов микросхем в ЦИП, снижает их стоимость. Это приводит к сдвигу точки пересечения кривых в координатах «стоимость» и «сложность» влево, что еще в большей степени расширяет зону, в которой более экономичны цифровые измерительные приборы.

4. СПИСОК ЛИТЕРАТУРЫ

1. Атамалян Э. Г. Приборы и методы измерения электрических величин. М.: Высш. шк., 1986.

2. Б.П. Хромой, Ю.Г. Моисеев. Электрорадиоизмерения: Учебник для техникумов. – М.: Радио и связь, 1985 – 288 с.

3. Измерения на звуковых и ультразвуковых частотах. Курс лекций для студентов специальностей 7.091201 ”Акустические средства и системы”, 7.091202 ”Медицинские акустические и биоакустические приборы и аппараты”/ Сост. А. И. Бахин, И. С. Бачинская. – К.: НТУУ “КПИ”, 2008 – 124с.