Задача 4
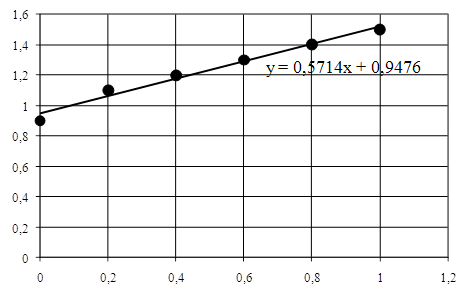
С помощью метода наименьших квадратов подобрать параметры a и b линейной функции y = a + bx, приближенно описывающей опытные данные из соответствующей таблицы. Изобразить в системе координат заданные точки и полученную прямую.
|
xi |
0,0 | 0,2 | 0,4 | 0,6 | 0,8 | 1,0 |
|
yi |
0,9 | 1,1 | 1,2 | 1,3 | 1,4 | 1,5 |
Решение
Система нормальных уравнений
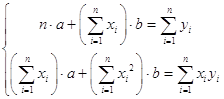
в задаче
n = 6
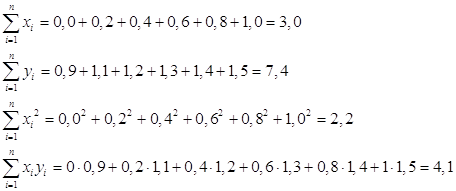
Тогда
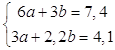
решая ее получаем 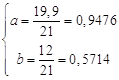 .
.
y = 0,5714x + 0,9476
Задача 5
Найти неопределенный интеграл ![]()
Решение
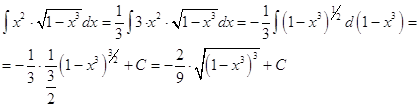
Ответ: ![]()
Задача 6
Найти неопределенный интеграл 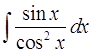
Решение
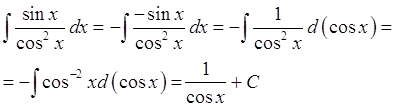
Ответ: 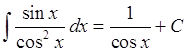
Задача 7
Найти неопределенный интеграл, применяя метод
интегрирования по частям ![]()
Решение
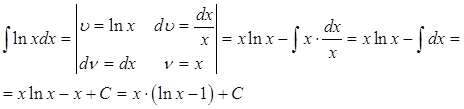
Ответ: ![]()
Задача 8
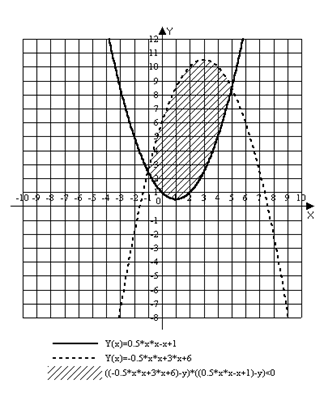
Вычислить площадь, ограниченную заданными параболами
![]()
Решение
Точки пересечения по х: х = -1, х = 5.
Площадь фигуры найдем из выражения
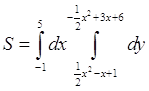
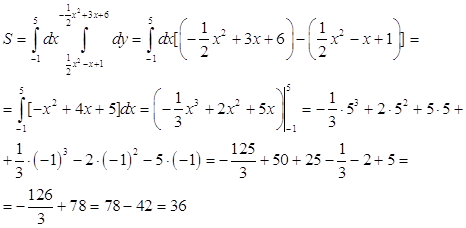
Ответ: ![]()
Задача 9
Найти общее решение дифференциального уравнения
первого порядка ![]()
Решение
Разделим переменные
![]()
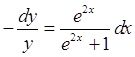
Проинтегрируем
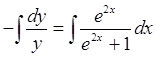
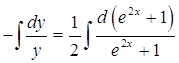
![]()
![]()
![]()
![]()
Ответ: ![]()
Задача 10
Найти частное решение линейного дифференциального уравнения первого порядка, удовлетворяющее начальному условию
![]()
![]()
Решение:
![]()
![]()
![]()
Запишем функцию y в виде произведения y = u * v. Тогда находим производную:
![]()
Подставим эти выражения в уравнение
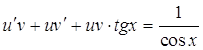
![]()
Выберем v таким, чтобы
![]()
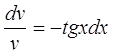
Проинтегрируем выражение
![]()
![]() ,
, ![]()
Найдем u
![]()
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]()
Тогда ![]()
![]()
Тогда ![]()
Ответ: ![]()
Задача 11
Исследовать на сходимость ряд:
а) с помощью признака Даламбера знакоположительный ряд
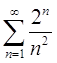
Решение
Проверим необходимый признак сходимости ряда
|
|
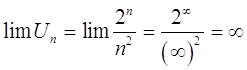
|
Используем признак Даламбера
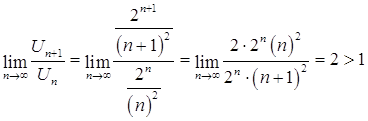
Ответ: ряд расходится
б) с помощью признака Лейбница знакочередующийся ряд
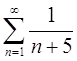
Решение
Проверим необходимый признак сходимости ряда
|
|
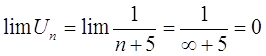
|
По признаку подобия
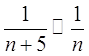
данный ряд аналогичен гармоническому ряду начиная с пятого члена, таким образом, т.к. гармонический ряд расходится, то и исходный ряд расходится.
Ответ: ряд расходится
в) Найти радиус сходимости степенного ряда и определить тип сходимости ряда на концах интервала сходимости
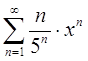
Решение
Используем признак Даламбера:
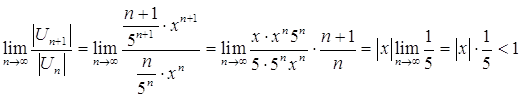
![]()
![]()
При х =5 получим ряд
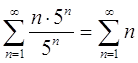
Ряд знакопостоянный, lim Un = n
Ряд расходится, так как состоит из суммы возрастающих элементов, каждый из которых больше 1.
При х = -5 получим ряд
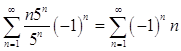
Ряд знакочередующийся, lim Un = n
|Un| > |Un+1| > |Un+2| … - не выполняется.
По теореме Лейбница данный ряд расходится
Ответ: Х Î (-5; 5)
Задача 12
Вычислить определенный интеграл с точностью до 0,001 путем предварительного разложения подынтегральной функции в ряд и почленного интегрирования этого ряда
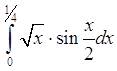
Решение
В разложении функции sin(x) в степенной ряд
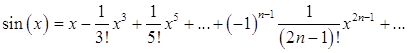
заменим 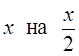 .
Тогда получим
.
Тогда получим
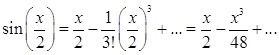
Умножая этот ряд почленно на ![]() будем
иметь
будем
иметь
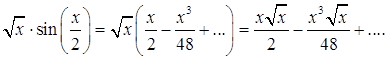
Следовательно
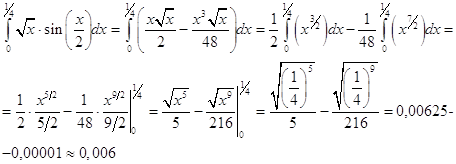
Ответ: » 0,006.














 (zip - application/zip)
(zip - application/zip)










