Реферат
Тема «Производная обратной функции и композиции функции»
Работу выполнила
студентка 22 группы
Васильева Анжелика
г.Бологое
Если поменять ролями аргумент и функцию, то x станет функцией от y. В этом случае говорят о новой функции, называемой обратной функцией.
Пусть задана функция 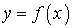 , что означает, что каждому числу
, что означает, что каждому числу 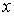 из некоторого множества поставлено в соответствие число
из некоторого множества поставлено в соответствие число 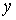 . Получаемые таким образом значения
. Получаемые таким образом значения 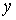 также образуют некоторое множество. Можно поставить задачу в
обратную сторону — по заданным значениям
также образуют некоторое множество. Можно поставить задачу в
обратную сторону — по заданным значениям 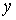 найти соответствующие им значения
найти соответствующие им значения 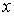 . И если каждому значению
. И если каждому значению 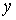 ставится в соответствие только одно значение
ставится в соответствие только одно значение 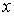 , то говорят, что определена обратная функция, обозначаемая
как
, то говорят, что определена обратная функция, обозначаемая
как 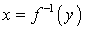 . Подчеркнем, что
. Подчеркнем, что 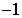 , находящаяся в степени, — это всего лишь обозначение
для обратной функции, которое вовсе не сводится к дроби
, находящаяся в степени, — это всего лишь обозначение
для обратной функции, которое вовсе не сводится к дроби 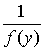 . Разумеется, можно использовать и любые другие символы для
обозначения обратной функции, например
. Разумеется, можно использовать и любые другие символы для
обозначения обратной функции, например 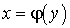 . Очевидно, что функция, обратная к обратной, дает исходную
функцию, поэтому
. Очевидно, что функция, обратная к обратной, дает исходную
функцию, поэтому 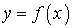 и
и 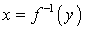 называют взаимно обратными функциями.Если функция
называют взаимно обратными функциями.Если функция 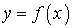 только возрастает или только убывает на некотором множестве
значений
только возрастает или только убывает на некотором множестве
значений 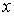 , то на соответствующем множестве значений
, то на соответствующем множестве значений 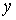 каждому значению
каждому значению 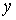 будет соответствовать только одно значение
будет соответствовать только одно значение 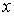 , то есть будет определена обратная функция
, то есть будет определена обратная функция 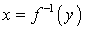
.Пример
1.Задана функция 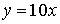 . Область определения и область значений функции — вся
числовая прямая. Обратная к ней функция будет
. Область определения и область значений функции — вся
числовая прямая. Обратная к ней функция будет 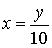
.Пример 2.Задана функция 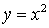 . Область определения — вся числовая прямая, а область
значений — только неотрицательные значения
. Область определения — вся числовая прямая, а область
значений — только неотрицательные значения 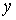 . Очевидно, что одному и тому же положительному значению
. Очевидно, что одному и тому же положительному значению 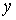 будут соответствовать два различных (отличающихся знаком) значения
будут соответствовать два различных (отличающихся знаком) значения 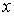 . Таким образом, мы можем определить две обратных функции,
каждая из которых будет соответствовать той или иной ветви параболы
. Таким образом, мы можем определить две обратных функции,
каждая из которых будет соответствовать той или иной ветви параболы 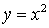 , то есть обратными будут функции
, то есть обратными будут функции 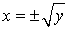 .
.
Пример.
Найти функцию
обратную для 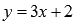 .
.
Решение.
Областью определения и
областью значений этой функции является все множество действительных чисел.
Выразим xчерез y(другими словами, решим
уравнение 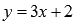 относительно x).
относительно x).
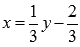 - это и есть обратная функция, правда
здесь y– аргумент, а x– функция этого аргумента.
Чтобы не нарушать привычки в обозначениях (это не имеет принципиального
значения), переставив буквы xи y, будем писать
- это и есть обратная функция, правда
здесь y– аргумент, а x– функция этого аргумента.
Чтобы не нарушать привычки в обозначениях (это не имеет принципиального
значения), переставив буквы xи y, будем писать 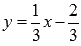 .
.
Таким образом, 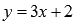 и
и 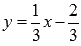 - взаимно обратные функции.
- взаимно обратные функции.
Приведем графическую иллюстрацию взаимно
обратных линейных функций.
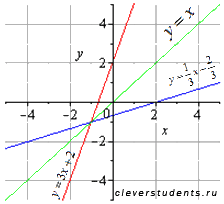
Очевидно, что графики симметричны относительно прямой y=x (биссектрисы первого и третьего квадрантов).
Теорема о производной обратной функции. Пусть 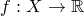 ,
,  обратима,
обратима, 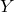 – множество значений
– множество значений 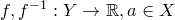 . Пусть функция
. Пусть функция  дифференцируема в точке
дифференцируема в точке 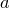 , а
функция
, а
функция 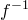 дифференцируема
в точке
дифференцируема
в точке 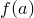 . Тогда
. Тогда 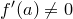 и
и 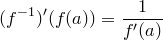 .
.
Доказательство.  .
.
Обозначим 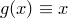 . Тогда
. Тогда
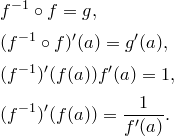
Формулы дифференцирования функций.

Дифференцирование функции
Операция нахождения производной функции называется дифференцированием этой функции.
Функция 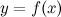 имеет
производную на интервале
имеет
производную на интервале 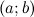 или называется дифференцируемой
в этом интервале, если производная
или называется дифференцируемой
в этом интервале, если производная 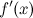 существует в каждой точке этого
интервала.
существует в каждой точке этого
интервала.
Функция 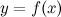 имеет в точке
имеет в точке  бесконечную
производную, если в этой точке
бесконечную
производную, если в этой точке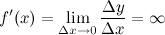 .
.
(О непрерывности функции в точке)
Если функция 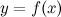 имеет конечную производную в точке
имеет конечную производную в точке 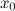 , то она непрерывна в этой точке.
, то она непрерывна в этой точке.
Замечание. Обратное заключение не всегда верно:
если функция 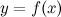 непрерывна в некоторой точке
непрерывна в некоторой точке 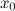 , то она может и не иметь производной
в этой точке.
, то она может и не иметь производной
в этой точке.
Функция 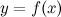 называется дифференцируемой
в точке
называется дифференцируемой
в точке  ,
если приращение функции, соответствующее приращению аргумента, можно
представить в виде:
,
если приращение функции, соответствующее приращению аргумента, можно
представить в виде:
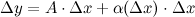
где 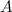 - число, не зависящее от
- число, не зависящее от 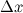 ,
, 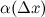 - б.м. функция при
- б.м. функция при 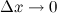 .
.
(О необходимом и достаточном условии дифференцируемости)
Для того чтобы функция 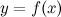 была дифференцируемой в точке
была дифференцируемой в точке  , необходимо
и достаточно, чтобы
, необходимо
и достаточно, чтобы 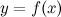 имела в этой точке конечную
производную.
имела в этой точке конечную
производную.
Теорема устанавливает, что для
функции 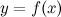 дифференцируемость в данной точке
дифференцируемость в данной точке  и существование конечной производной
в этой точке - понятия равносильные.
и существование конечной производной
в этой точке - понятия равносильные.














 (zip - application/zip)
(zip - application/zip)










