ПРОИЗВОДНАЯ_1
|
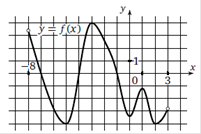
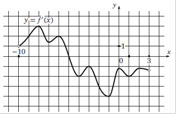
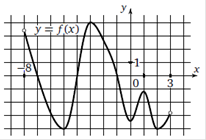
На рисунке изображен график функции y = f(x), определенной на интервале (−8; 3). 1) Найдите количество точек, в которых производная функции f (x) равна 0. 2) Найдите количество точек, в которых касательная к графику функции параллельна прямой y = 18.
Ответ. 5 |
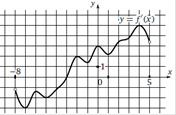
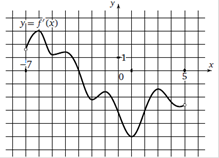
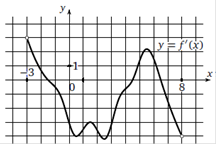
На рисунке изображен график производной функции f(x), определенной на интервале (−8; 5). В какой точке отрезка [0;4] f(x) принимает наименьшее значение?
1. Отметим отрезок [0;4] 2. Производная положительная – функция возрастает. 3. Наименьшее значение принимает в точке 0. Ответ. 0 |
На рисунке изображен график производной функции f(x), определенной на интервале (−10; 3). В какой точке отрезка [−4;−1] f(x) принимает наибольшее значение?
1. Отметим отрезок [−4;−1] 2. Производная отрицательная – функция убывает. 3. Наибольшее значение принимает в точке -4. Ответ. -4 |
|
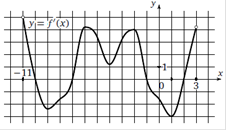
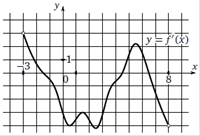
На рисунке изображен график производной функции f(x), определенной на интервале (−11;3). Найдите количество таких чисел xi, что касательная к графику функции f(x) в точке с абсциссой xi параллельна прямой y = 3x − 11 или совпадает с ней.
y = 3x – 11 y¢ = 3 Ответ. 6 |
На рисунке изображен график производной функции f(x), определенной на интервале (−5; 3). Найдите абсциссу точки, в которой касательная к графику функции f (x) параллельна прямой y = 2x+7 или совпадает с ней.
1. Найдем производную y = 2x+7 y¢ = 2 2. Проведем прямую y¢ = 2 3. Найдем абсциссу (х) точки пересечения прямой с графиком производной Ответ. -1 |
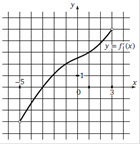
На рисунке изображен график функции f(x). Касательная к этому графику, проведенная в точке с абсциссой 4, проходит через начало координат. Найдите f ¢(4).
1. Проходит через начало координат – точка (0;0) 2. Абсцисса 4 – находим ординату = 6 – точка (4;6) 3. Воспользуемся формулой Ответ. 1,5 |
|
На рисунке изображен график функции y = f(x), определенной на интервале (−8;3). Определите количество целых чисел xi, для которых f ¢(xi) отрицательно.
1. Производная отрицательная, если функция убывает. 2. Сосчитаем количество целых чисел xi (yi может быть не целым числом) Ответ. 4 |
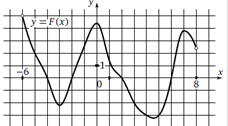
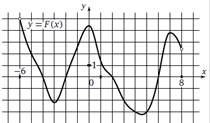
На рисунке изображен график y =F(x) одной из первообразных некоторой функции f, определенной на интервале (−6;8). 1. Определите количество целых чисел xi, для которых f (xi) положительно.
2. Найдите количество точек, в которых f (x)=0.
Функция – производная Первообразная - функция |
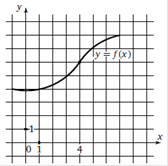
Прямая, изображенная на рисунке, является графиком одной из первообразных функции y = f(x). Найдите f (1).
1. Найдем целые координаты двух любых точек. 2. Например, (1;3) и (-1;5) 3. Воспользуемся формулой Ответ. -1 |
ПРОИЗВОДНАЯ_2
|
На рисунке изображен график производной функции f(x), определенной на интервале (−7;5). Найдите точку экстремума функции f(x), принадлежащую отрезку [−6;4].
1. Отметим отрезок [−6;4]. 2. Экстремум – точки максимум и минимум (производная меняет знаки с «+» на «-» или с «-» на «+». 3. Найти точку – определить x. Ответ. -3 |
На рисунке изображен график производной функции f(x), определенной на интервале (−3;8). Найдите количество точек максимума функции f (x), принадлежащих отрезку [−2; 7].
1. Отметим отрезок [−2;7]. 2. Точка максимум функции – производная меняет знак с «+» на «-». Таких точек 2. Ответ. 2 |
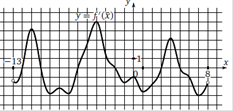
На рисунке изображен график производной функции f(x), определенной на интервале (−13;8). Найдите количество точек минимума функции f (x), принадлежащих отрезку [−8; 6].
1. Отметим отрезок [−8;6]. 2. Точка минимум функции – производная меняет знак с «-» на «+». Таких точек 2. Ответ. 2 |
|
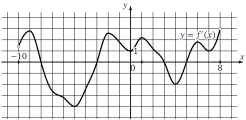
На рисунке изображен график производной функции f (x), определенной на интервале (−10; 8). Найдите количество точек экстремума функции f(x), принадлежащих отрезку [−9; 7].
1. Отметим отрезок [−9;7]. 2. Отметим точки, где производная меняет знаки. Таких точек 4. Ответ. 4 |
На рисунке изображен график производной функции f(x), определенной на интервале (−3;8). Найдите промежутки убывания функции f (x). В ответе укажите сумму целых чисел, входящих в эти промежутки.
1. Функция убывает – производная меньше нуля (отрицательная). 2. Отметим промежутки – их два: [−1,5; 4,5] и [6,5; 8). 3. Целые числа, входящие в эти промежутки — это −1; 0; 1; 2; 3; 4; 7 (значения х). 4. Искомая сумма равна −1+0+1+2+3+4+7=16. Ответ. 16 |
На рисунке изображен график производной функции f(x), определенной на интервале (−11;3). Найдите промежутки возрастания функции f (x). В ответе укажите длину наибольшего из них.
1. Функция возрастает – производная больше нуля (положительная). 2. Отметим промежутки – их три: (−11;−10], [−7;−1] и [2;3) 3. Наибольшую длину имеет промежуток [−7;−1] - длина равна 6. Ответ. 6 |
|
Прямая y=4x +13 параллельна касательной к графику функции y = x2−3x +5. Найдите абсциссу точки касания. Решение. 1. y=4x +13, y¢=4 y = x2−3x +5, y¢ = 2x−3 2. 2x−3 = 4 x = 3,5 Ответ. 3,5 |
Прямая y= 2x + 37 является касательной к графику функции y = x3+3x2−7x +10. Найдите абсциссу точки касания. Решение. 1. y= 2x + 37, y¢=2 y = x3+3x2−7x +10, y¢=3x2+6x-7 2. 3x2+6x-7 = 2 x = -3; x = 1 3. Проверка 1) x = -3; 2·(-3) + 37 = 31 (-3)3+3· (-3)2 -7·(-3)+10= = -27+27+21+10 = 31 31=31 – верно 2) x = 1; 2· 1 + 37 = 39 13+3· 12 -7·1+10= = 1+3-7+10 = 7 39=7 – неверно Ответ. -3 |
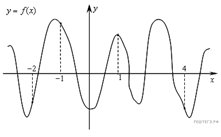
На рисунке изображен график функции y = f(x)и отмечены точки −2, −1, 1, 4. В какой из этих точек значение производной наименьшее? В ответе укажите эту точку.
Чем больше угол, тем больше значение (угол острый – положительное значение, угол тупой – отрицательное) 1. Провести касательные в точках. 2. Значение произв. наименьшее – выбрать тупые углы (в точках -1 и 4) Ответ. 4 |


























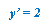


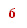


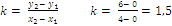



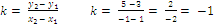













 (zip - application/zip)
(zip - application/zip)










