Государственное образовательное учреждение
высшего профессионального образования
«Санкт-Петербургский государственный политехнический университет»
Факультет экономики и менеджмента
Кафедра "Предпринимательство и коммерция"
Курсовой проект
по дисциплине «Статистика»
на тему «Анализ рядов динамики»
Выполнил: Кийко И.В. гр. 33707/3
_________________________
(подпись)
Принял: _____________________
Пономарева О.А.
___________________________
(подпись)
___________________________
(Дата)
Санкт-Петербург
2016
Кийко И.В.. Статистический анализ временных рядов: Курсовой проект по дисциплине «Статистика». СПб.: СПбГПУ, 2016, стр 57, табл. _, рис. _.
ДИНАМИЧЕСКИЕ РЯДЫ, ПОКАЗАТЕЛИ ИЗМЕНЕИЯ УРОВНЕЙ ВРЕМЕННЫХ РЯДОВ, СРЕДНИЕ ХАРАКТЕРИСТИКИ ВРЕМЕННОГО РЯДА, ОСНОВНАЯ ТЕНДЕНЦИЯ, ТРЕНДОВАЯ МОДЕЛЬ, КОРЕЛЯЦИЯ РЯДОВ ДИНАМИКИ, ПРОГНОЗИРОВАНИЕ, ТОЧЕЧНЫЙ ПРОГНОЗ, УРАВНЕНИЕ ТРЕНДА, АВТОКОРЕЛЯЦИЯ, УРОВНИ РЯДА, ТЕНДЕНЦИЯ
В курсовом проекте произведен статистический анализ объемов экспорта и импорта Испании за период с 1977 года по 20012 год. Рассчитаны показатели скорости и интенсивности изменения объемов экспорта и импорта Испании. Построены трендовые и авторегрессионные модели.
СОДЕРЖАНИЕ
Введение……………………………………………………………………
Исходные данные…………………………………………………………..
1. Расчет показателей изменения уровней динамического ряда………..
1.1. Графическое представления показателей изменения уровней……..
2. Расчет и анализ средних характеристик динамического ряда………..
3. Механическое выравнивание динамических рядов…………………...
4. Построение трендовой модели и прогнозирование…………………...
4.1. Построение трендовых моделей для ряда экспорт………………….
4.2. Построение трендовых моделей для ряда импорт…………………..
5. Автокорреляция в динамических рядах. Авторегрессионные модели
5.1.Автокорреляция в остатках ряда экспорт и импорт…………………
5.2. Построение авторегрессиионной модели……………………………
6. Корреляции рядов динамики……………………………………………
6.1. Зависимость экспорта от импорта и от времени…………………….
6.2. Зависимость импорта от экспорта и о времени……………………...
Заключение…………………………………………………………………
Список использованных источников……………………………………..
Введение
Важнейшей задачей практической статистики, а также менеджеров разных уровней является построение и анализ рядов динамики.
Ряды динамики – это расположенные в хронологическом порядке значения того или иного показателя, изменение которого отражает ход развития изучаемого явления. Их также называют динамическими рядами, временными рядами.
В каждом ряду динамики имеется два основных элемента: показатель времени «t», соответствующие им уровни развития изучаемого явления «y».
В качестве показаний времени в рядах динамики выступают либо определенные даты (моменты), либо отдельные периоды (года, кварталы, месяцы, сутки).
По времени, отражаемому в динамических рядах, они разделяются на моментные и интервальные.
1. Моментные - ряды динамики, в которых уровни ряда выражают величины статистического показателя, зафиксированные на определенные даты, моменты времени.
2. Интервальные - отражают итоги развития изучаемых явлений за отдельные периоды, интервалы времени.
Общий вид ряда можно представить следующим образом:
У1, У2, У3, … , Уt, … , Уn , где
t – момент или период времени;
n – длина динамического ряда (число уровней ряда).
В данной работе рассмотрено и проанализировано поведение показателей экспорта и импорта Испании с 1977 по 2012 год.
1. Анализ рядов динамики
|
Экспорт Испания |
Импорт Испания |
|
|
1977 |
10223,4 |
17835,8 |
|
1978 |
13114 |
18711,6 |
|
1979 |
18208,3 |
25438,1 |
|
1980 |
20720,1 |
34078,4 |
|
1981 |
20333,2 |
32150,4 |
|
1982 |
20497,7 |
31465,3 |
|
1983 |
19733,8 |
29192,6 |
|
1984 |
23564,5 |
28830,5 |
|
1985 |
24246,9 |
29963,3 |
|
1986 |
27206,3 |
35056,7 |
|
1987 |
34192,3 |
49112,5 |
|
1988 |
40341,2 |
60502,2 |
|
1989 |
43450,6 |
70945,4 |
|
1990 |
55521,4 |
87554,2 |
|
1991 |
58621 |
92965,4 |
|
1992 |
64839,9 |
99752,6 |
|
1993 |
60955,1 |
79665,3 |
|
1994 |
72927 |
92191,1 |
|
1995 |
91045,6 |
113319 |
|
1996 |
101996 |
121782 |
|
1997 |
104359 |
122711 |
|
1998 |
109228 |
133149 |
|
1999 |
109964 |
144436 |
|
2000 |
113349,1 |
152903,1 |
|
2001 |
115178,5 |
153638,4 |
|
2002 |
123635,7 |
163672,4 |
|
2003 |
156035,1 |
208566 |
|
2004 |
182160,6 |
257676 |
|
2005 |
190991,5 |
287456,3 |
|
2006 |
213351,6 |
326049,4 |
|
2007 |
248917 |
384953,7 |
|
2008 |
277527 |
416788,7 |
|
2009 |
220909,7 |
290820,8 |
|
2010 |
246252,9 |
315521,2 |
|
2011 |
298522,5 |
362913,4 |
|
2012 |
283391,3 |
325587,4 |
1.1 Исходные данные
Объем экспорта и импорта Испании за период с 1977 по 2012 год в млрд. доллар.
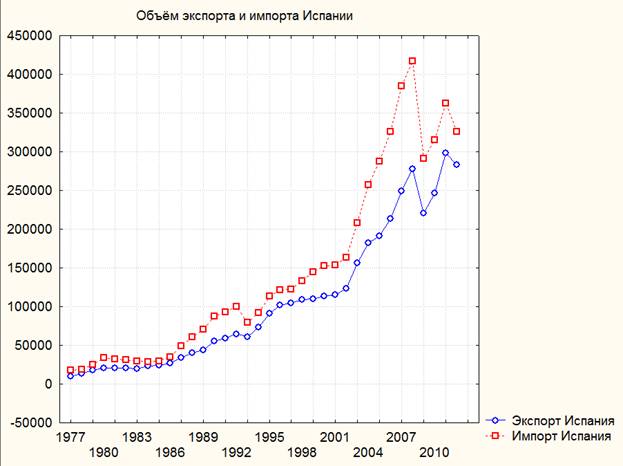
Рис. 1. Объем импорта и экспорта Испании за период с 1977 года по 2012 год в млрд. доллар.
1.2. Показатели изменения уровней динамического ряда
К показателям, оценивающих изменение уровней ряда динамики, относятся:
1. Абсолютный прирост может быть как положительным, так и отрицательным. Он показывает, насколько уровень текущего периода выше или ниже предшествующего и выражает абсолютную скорость роста или снижения уровней ряда.
2. Темп роста (коэффициентом роста) - это отношение последующего уровня к предыдущему или какому-либо другому, принятому за базу сравнения. Темп роста оценивает, во сколько раз уровень текущего периода выше или ниже уровня базисного периода, или сколько процентов он составляет по отношению к базисному.
3. Темп прироста показывает, на сколько процентов увеличились размеры явлений за изучаемый период времени. Темп прироста, выраженный в процентах, показывает на сколько процентов увеличился или уменьшился текущий уровень по сравнению с базисным, принятым за 100%, или, иначе, сколько процентов составляет абсолютный прирост данного уровня по отношению к базисному уровню.
4. Абсолютное значение 1% прироста. Оно представляет собой отношение величины абсолютного прироста к темпу прироста, выраженному в процентах. Этот показатель имеет большое значение в экономическом анализе, поскольку темпы роста могут иметь тенденцию к уменьшению или оставаться на одном уровне, а абсолютное значение одного процента прироста расти.
Показатели могут быть рассчитаны двумя методами:
1. Цепной.
На основе цепных показателей абсолютного прироста рассчитываются показатели ускорения изменения уровней рядов (разность двух соседних показателей абсолютного прироста):

2. Базисный.
Базисный абсолютный прирост определяется по следующей формуле:
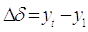
По цепному методу темп роста определяется путем деления уровня ряда на предыдущий:
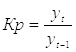
По базисному методу:

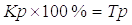
Kp - коэффициент роста
В данном разделе с помощью программы STATISTICA определены темпы роста, темпы прироста и абсолютные приросты экспорта и импорта Испании за период с 1977 по 2012 год, рассчитанные по базисному и цепному методам. Ниже на рисунке 2 представлены данные показатели для экспорта Испании, а на рисунке 3 данные показатели для импорта Испании.
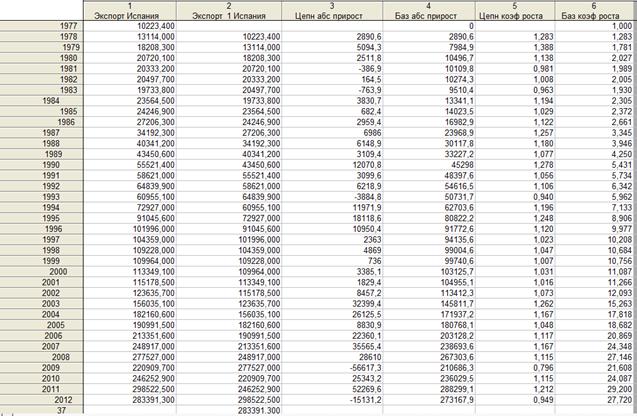
Рис. 2. Темпы роста, темпы прироста и абсолютные приросты экспорта Испании, рассчитанные по базисному и цепному методам
Рисунок 2 показывает:
1. В Испании в 2001 году объем экспорта увеличился на 1829,4 млрд. долларов по сравнению с 2000 годом.
2. В Испании в 2001 году объем экспорта увеличился на 104955,1 млрд. долларов по сравнению с 1977 годом.
3. В Испании в 2001 году объем экспорта составил 101,6% от объема экспорта в 2000 году, то есть объем экспорта в 2001 году увеличился по сравнению с 2000 годом в 1,016 раз.
4. В Испании в 2001 году объем экспорта составил 1126,6% от объема экспорта в 1977 года, то есть объем экспорта в 2001 году увеличился по сравнению с 1977 годом в 11,266 раз.
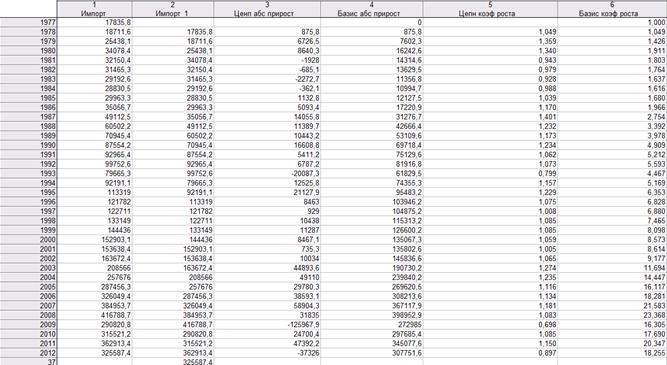
Рис. 3. Темпы роста, темпы прироста и абсолютные приросты импорта Испании, рассчитанные по базисному и цепному методам
Рисунок 3 показывает:
1. В Испании в 2001 году объем импорта увеличился на 735,3 млрд. долларов по сравнению с 2000 годом.
2. В Испании в 2001 году объем импорта увеличился на 135802,6 млрд. долларов по сравнению с 1977 годом.
3. В Испании в 2001 году объем импорта составил 100,5% от объема экспорта в 2000 году, то есть объем импорта в 2001 году увеличился по сравнению с 2000 годом в 1,005 раз.
4. В Испании в 2001 году объем импорта составил 861,4% от объема экспорта в 1977 года, то есть объем импорта в 2001 году увеличился по сравнению с 1977 годом в 8,614 раз.
1.3 Графическое представление рядов динамики
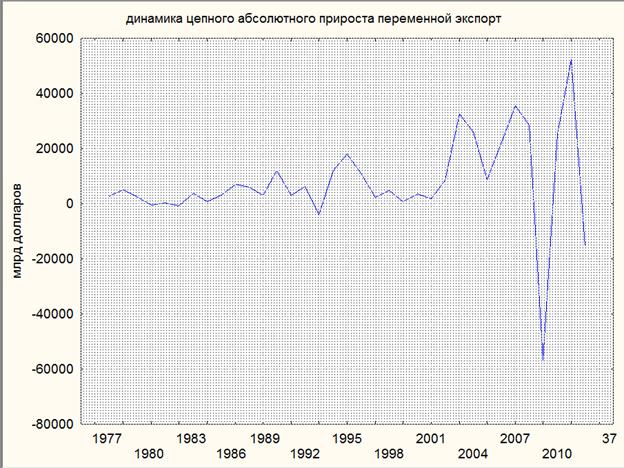
Рис. 4. Динамика цепного абсолютного прироста переменной "экспорт"
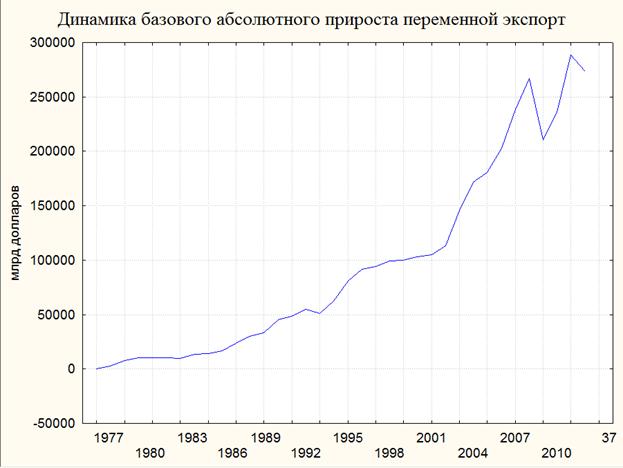
Рис. 5. Динамика базисного абсолютного прироста переменной "экспорт"
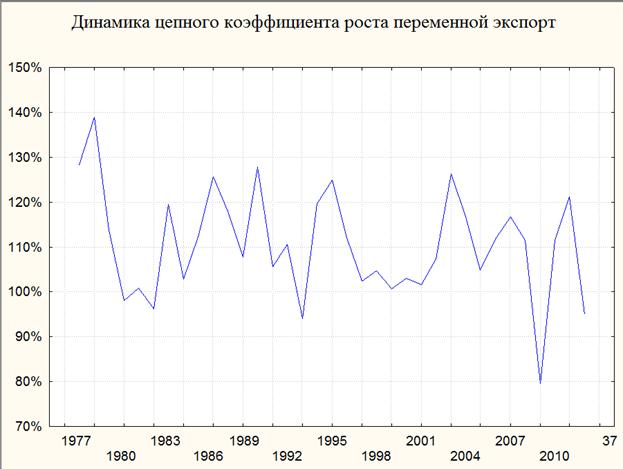
Рис. 6. Динамика цепного коэффициента роста переменной "экспорт"
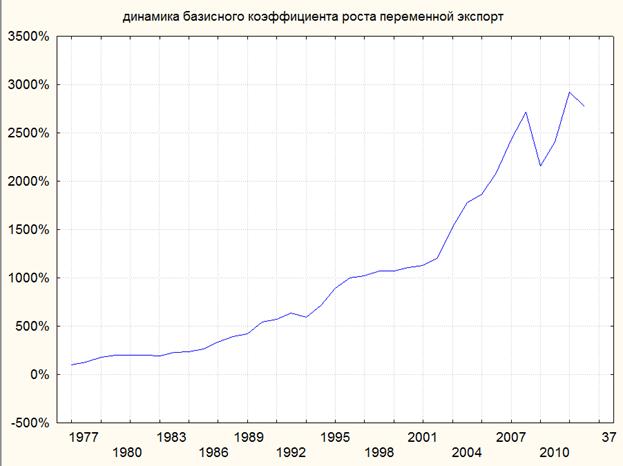
Рис. 7. Динамика базисного коэффициента роста переменной "экспорт"
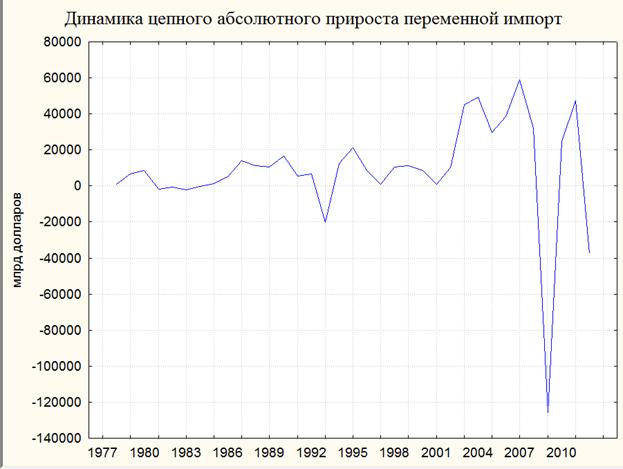
Рис. 8. Динамика цепного абсолютного прироста переменной "импорт"
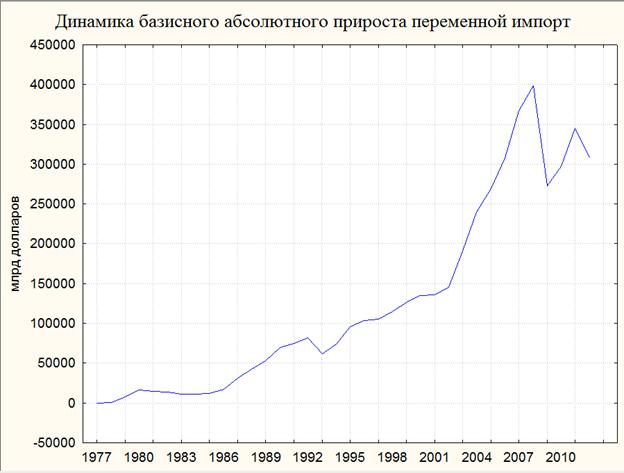
Рис. 9. Динамика базисного абсолютного прироста переменной "импорт"

Рис. 10. Динамика цепного коэффициента роста переменной "импорт"
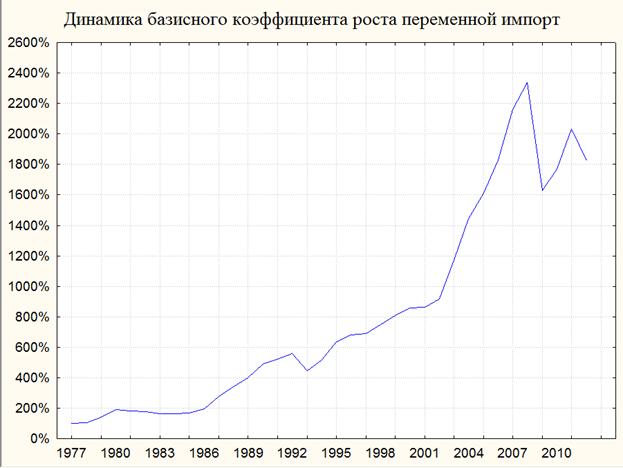
Рис. 11. Динамика базисного коэффициента роста переменной "импорт"
Рассчитанные абсолютные и относительные показатели динамики варьируют, изменяются во времени. Это обстоятельство вызывает необходимость расчета обобщающих характеристик, которыми являются средние показатели.
2. РАСЧЁТ И АНАЛИЗ СРЕДНИХ ХАРАКТЕРИСТИК ВРЕМЕННОГО РЯДА
Рассчитанные абсолютные и относительные показатели динамики варьируют, изменяются во времени. Это обстоятельство вызывает необходимость расчета обобщающих характеристик, которыми являются средние показатели.
Средний уровень ряда для интервальных рядов рассчитывается на основе средней арифметической простой, т.е. суммируются все элементы ряда.
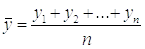
Средний абсолютный прирост рассчитывается на основе цепных абсолютных приростов и характеризует, на сколько в среднем в единицу времени изменилось уровней изучаемого ряда.

Средний коэффициент роста рассчитывается на основе средней геометрической и характеризует во сколько раз в среднем, в единицу времени, изменилось уровней изучаемого ряда.

Средний темп прироста характеризует, на сколько % в среднем в единицу времени изменяются уровни ряда.
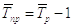 (в виде
коэффициентов) и
(в виде
коэффициентов) и  .
.
Рассчитаем описанные выше показатели в программе STATISTICA.
В Таблице 2.1. и Таблице 2.2. вычислены разнообразные статистики, включая нужные нам:
- геометрическая средняя, для расчета среднего коэффициента роста;
- средняя арифметическая, для расчета среднего уровня за период и среднего абсолютного прироста.
В данных таблицах Mean – средняя арифметическая, Geometric –средняя геометрическая.
Таблица 2.1.
Средние показатели экспорта Испании за период с 1977 по 2012 год

Таблица 2.1. Показывает:
1. (Средней коэффициент роста) В Испании объем экспорта за период с 1977 по 2012 год, в среднем в год увеличивался в 1,1 раз.
2. (Средний уровень ряда) В Испании за период с 1977 по 2012 год среднегодовой объем экспорта составил 105986,4 млн. долларов
3. (Средний абсолютный прирост) В Испании объем экспорта за период с 1977 по 2012 год, в среднем в год увеличивался на 7804,8 млн. долларов.
Таблица 2.2.
Средние показатели импорта Испании за период с 1977 по 2012 год
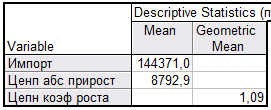
Таблица 2.2. Показывает:
1.(Средней коэффициент роста) В Испании объем импорта за период с 1977 по 2012 год в среднем в год увеличивался в 1,09 раз.
2. (Средний уровень ряда) В Испании за период с 1977 по 2012 год среднегодовой объем импорта составил 144371 млн. долларов
3. (Средний абсолютный прирост) В Испании объем импорта за период с 1977 по 2012 год, в среднем в год увеличивался на 8792,9 млн. долларов.
В таблице 2.3. проведен сравнительный анализ импорта и экспорта Испании. Объем импорта по всем средним показателям опережает объем импорта. То есть в Испании за период с 1977 года по 2012 год больше ввозились иностранные товары, чем вывозились за границу. Можно предположить, что такая тенденция сохранится и на последующие года.
Таблица 2.3
Сравнительный анализ среднегодовых показателей объемов экспорта и
импорта Испании за период с 1977 по 2012 год
|
Средний уровень ряда |
Средний коэффициент роста |
Средний абсолютный прирост |
Средний темп прироста |
|
|
Экспорт |
105986,4 |
1,1 |
7804,8 |
10% |
|
Импорт |
144371 |
1,09 |
8792,9 |
9% |
3. Механическое выравнивание динамических рядов
Значения уровней
динамического ряда формируются под влиянием целого ряда факторов. Уровень динамического ряда может быть представлен как
функция четырёх компонент: 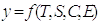 .
.
Где:
Т – трендовая компонента сформирована под влиянием факторов, постоянно влияющих на протяжении длительного периода времени и формирующих основную тенденцию ряда (тренд);
S – сезонная компонента сформирована под влиянием факторов, действующих на уровни ряда с определенной периодичностью;
C – циклическая компонента сформирована под влиянием сезонных факторов, влияющих на динамические ряды, построенные по внутригодичным данным (за месяц, сезон);
E – случайная компонента сформирована под влиянием факторов, влияние которых очень трудно оценить из-за отсутствия периодичности.
Чем больше влияние нетрендовых компонент, тем сложнее оценить основную тенденцию временного ряда, для выявления которой используются два метода.
1. Механическое выравнивание – предполагают использование либо метода укрупненных интервалов, либо по методу скользящей средней.
2. Аналитический метод выравнивания – позволяет получить аналитическую функцию основной тенденции ряда (уравнение тренда).
Основные процедуры механического выравнивания: метод укрупненных интервалов и метод скользящей средней.
1. Метод укрупненных интервалов, предполагает объединение временных интервалов и расчет либо суммарного значения по ним либо среднего значения.
2. Метод скользящей средний, предполагает определение средних величин в ограниченном временном интервале, который скользит по динамическому ряду. Применение данного метода, позволяет сгладить периодические и случайные колебания и тем самым выявить присутствующую в развитии тенденцию.
Пусть динамический ряд состоит из уровней yt, t = 1, ..., n. Для каждых m последовательных уровней этого ряда (т < n) можно подсчитать среднюю величину. Вычислив значение средней для первых т уровней, переходят к расчету средней для уровней y2, ..., yт+i, затем y3, ..., ym+2 и т. д. Таким образом, интервал сглаживания, т. е. интервал, для которого подсчитывается средняя, как бы скользит по динамическому ряду с шагом, равным единице. Если т нечетное число, а предпочтительнее брать именно нечетное число уровней, поскольку в этом случае расчетное значение уровня окажется в центре интервала сглаживания и им легко заменить конкретное фактическое значение, то для определения скользящей средней можно записать следующую формулу:
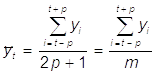
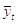 - значение
скользящей средней для момента t,
- значение
скользящей средней для момента t,
yi - фактическое значение уровня в момент i;
i - порядковый номер уровня в интервале сглаживания;
m - интервал сглаживания (период скольжения).
Величина р определяется из продолжительности интервала сглаживания. Поскольку т = 2р+ 1 при нечетном т, то
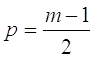 .
.
Проведем выравнивания динамических рядов экспорта и импорта Австрии в программе STATISTIKA.
Требуется провести сглаживание динамического ряда 3-х и 7-ми членными скользящими средними.
Таблица 3.1.
Сглаживание динамического ряда экспорта 3-х и 5-ти членными скользящими средними.
Графическое представление выравнивая динамического ряда экспорта.
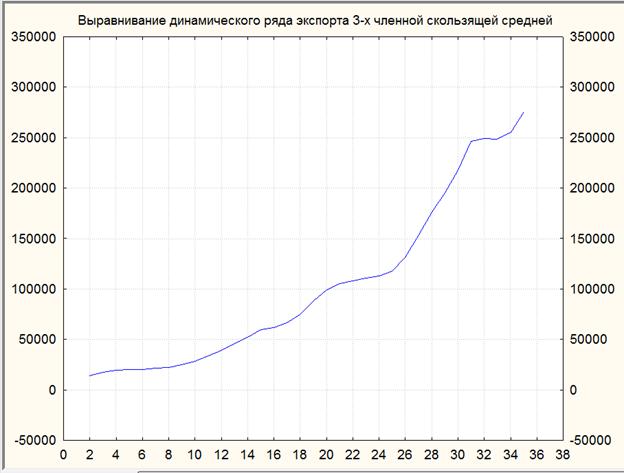
Рис. 3.1. Выравнивание динамического ряда экспорта 3-х членной скользящей средней
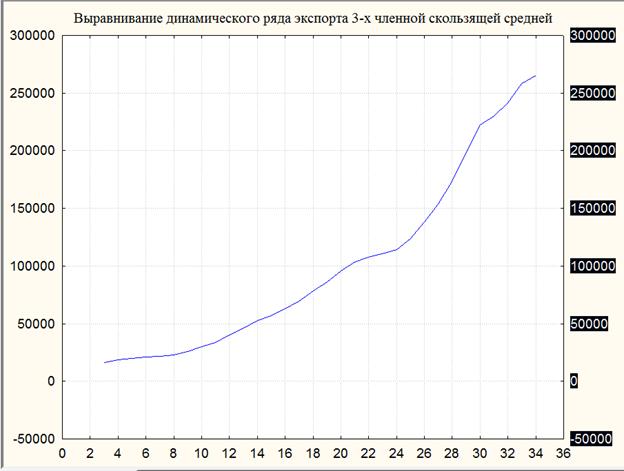
Рис. 3.2. Выравнивание динамического ряда экспорта 5-ти членной скользящей средней
Графическое представление выравнивая динамического ряда импорта.
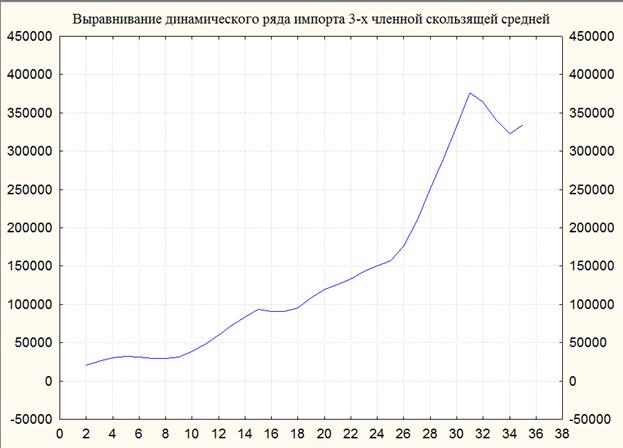
Рис. 3.3. Выравнивание динамического ряда импорта 3-х членной скользящей средней

Рис. 3.4. Выравнивание динамического ряда импорта 5-ти членной скользящей средней














 (zip - application/zip)
(zip - application/zip)










