Міністерство освіти і науки України
Сумський Державний Університет
Курсова робота
з дисципліни
«Теорія алгоритмів та математична логіка»
На тему
«Знаходження мінімального остовом дерева. Порівняння алгоритму Прима і алгоритму Крускала»
Виконав студент
факультету ЕлІТ групи ІН-83
Горбатенко О. О.
Перевірив Кузіков Б. О.
Суми 2010
Завдання роботи
При виконанні ОДЗ необхідно реалізувати алгоритми Прима та Крускала побудови остового дерева у графі, та протестувати її на тестовому графі наведеному у завданнях до ОДЗ згідно вашого варіанту. У пояснювальній записці до ОДЗ повинно бути викладено наступне:
• Вступ. Короткі відомості про поняття остового дерева;
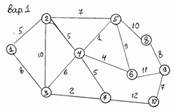
• Завдання роботи, Включаючи тестовий приклад графу, згідно варіанта;
• Алгоритм Прима:
◦ короткі відомості про алгоритм та асимптотичну оцінку його швидкодії, спосіб представлення графу та його обґрунтування (10%);
◦ остове дерево, отримане за допомогою алгоритму (5%);
◦ фактичні параметри швидкодії (кількість порівнянь) для тестового прикладу (10%);
◦ оцінку швидкодії реалізованого варіанта алгоритму (10%).
• Алгоритм Крускала:
◦ короткі відомості про алгоритм та асимптотичну оцінку його швидкодії, спосіб представлення графу та його обґрунтування(10%);
◦ остове дерево, отримане за допомогою алгоритму (5%);
◦ фактичні параметри швидкодії (кількість порівнянь) для тестового прикладу (10%);
◦ оцінку швидкодії реалізованого варіанта алгоритму (10%).
• Порівняння алгортимів, контрольні приклади:
◦ висновок що до умов, коли доцільно використовувати той чи інший алгоритм (10%)
◦ довільний граф (10 або більше вершин), на якому алгоритм Прима дає перевагу, навести фактичні параметри швидкодії (10%);
◦ довільний граф (10 або більше вершин), на якому алгоритм Крускала дає перевагу, навести фактичні параметри швидкодії (10%).
Поставлене завдання: маючи на вході граф G, одержати на виході його остовне дерево мінімальної вартості, використати алгоритми Крускала й Прима. Порівняти використовувані алгоритми.
Вступ
Нехай G = (V, Е) — зв"язний граф, у якому кожне ребро (u,v ) позначено числом c(u, v), що називається вартістю ребра. Остовним деревом графа G називається вільне дерево, що містить всі вершини V графа G. Вартість остовного дерева обчислюється як сума вартостей всіх ребер, що входять у це дерево.
Типове застосування остовних дерев мінімальної вартості можна знайти при розробці комунікаційних мереж. Тут вершини графа представляють міста, ребра - можливі комунікаційні лінії між містами, а вартість ребер відповідає вартості комунікаційних ліній. У цьому випадку остовне дерево мінімальної вартості представляє комунікаційну мережу, що поєднує всі міста комунікаційними лініями мінімальної вартості.
Існують різні методи побудови остовних дерев мінімальної вартості. Багато хто з них ґрунтуються на наступній властивості остовних дерев мінімальної вартості. Нехай G = (V, Е) — зв"язний граф із заданою функцією вартості, що задана на множині ребер. Позначимо через U підмножину вершин V. Якщо (і, v) — таке ребро найменшої вартості, що й належить U і v належить V U, тоді для графа G існує остовное дерево мінімальної вартості, що містить ребро (і, v).
Існують два популярних алгоритми побудови остовного дерева мінімальної вартості для позначеного графа G = (V, Е), основані на описаній властивості: Прима й Крускала. Обидва алгоритми відповідають «жадібній» стратегії: на кожному кроці вибирається локально найкращий варіант.
Алгоритм Прима поступово будує шуканий мінімальний остов, додаючи до нього по одному ребру на кожному кроці (Це означає, що алгоритм Прима є жадібним. Більш того, справедливість алгоритму Прима легко встановлюється в рамках теорії матроідов.). На початку роботи алгоритму результуюче дерево складається з однієї вершини (її можна вибирати довільно). Алгоритм складається з N-1 ітерації, на кожній з яких до дерева додається рівно одне ребро, не порушує властивості дерева (тобто один кінець додається ребра належить дереву, а інший - не належить). Ключовий момент - з усіх таких ребер кожен раз вибирається ребро з мінімальною вагою. Така реалізація працює за O (MN).
Покращена реалізація буде виконуватися помітно швидше - за O (M log N + N2).
Для цього ми відсортуємо всі ребра в списках суміжності кожної вершини по збільшенню ваги (буде потрібно O (M log M) = O (M log N)). Крім того, для кожної вершини заведемо покажчик, який вказує на перше доступне ребро в її списку суміжності. Спочатку всі покажчики вказують на початку списків, тобто рівні 0. На i-ої ітерації алгоритму Прима ми перебираємо всі вершини, і вибираємо найменше за вагою ребро серед доступних. Оскільки всі ребра вже відсортовані за вагою, а покажчики вказують на перші доступні ребра, то вибір найменшого ребра здійсниться за O (N). Тепер нам слід оновити покажчики, оскільки деякі з них вказують на що стали недоступними ребра (обидва кінці яких опинилися всередині дерева), тобто зрушити деякі з них праворуч. Проте, оскільки у всіх списках суміжності в сумі 2 * M елементів, а покажчики зсуваються тільки вправо, то виходить, що на підтримку всіх покажчиків потрібно O (M) дій. Разом - час виконання алгоритму O (MlogM + N2 + M), тобто O (M log N + N2)
Код алгоритму:
void prim()
{
int i, min, j, k;
pr_count=0;
sr_count=0;
k = 0;
v[0]= 1;
for (i = 1;i< n;i++)
{
d[i] = a[i][0];
p[i] = 0;
}
for
(i = 0;i { min
= inf; for
(j = 0;j< n;j++) if
((v[j]!=1) && (d[j] < min)) { sr_count++; min
= d[j]; pr_count++; k
= j; pr_count++; } printf("%d
%d
",k+1, p[k]+1); mst_weight+=a[k][p[k]]; v[k]
= 1; for
(j = 0;j< n;j++) if
((v[j]!=1) && (d[j] > a[k][j])) { sr_count++; p[j]
= k; pr_count++; d[j]
= a[k][j]; pr_count++; } } } Результат
роботи програми: Алгоритм
Крускала Алгоритм
Крускала спочатку поміщає кожну вершину в своє дерево, а потім поступово
об"єднує ці дерева, об"єднуючи на кожній ітерації два деяких дерева деяким
руба. Перед початком виконання алгоритму, усі ребра сортуються за вагою (в
порядку неубиванія). Потім починається процес об"єднання: перебираються всі
ребра від першого до останнього (у порядку сортування), і якщо у поточного
ребра його кінці належать різним піддерев, то ці піддерев об"єднуються, а ребро
додається до відповіді. Після закінчення перебору всіх ребер всі вершини
опиняться належать одному піддереві, і відповідь знайдений. Сортування
ребер потребують O (M log N) операцій. Приналежність вершини того чи іншого
піддереві зберігається просто за допомогою масиву, об"єднання двох дерев
здійснюється за O (N) простим проходом по масиву. Враховуючи, що всього
операцій об"єднання буде N-1, ми й отримуємо асимптотики O (M log N + N2). Покращена
реалізація використовує структуру даних "Система непересічних множин"
позволет домогтися асимптотики O (M log N). Так само, як і в простій версії
алгоритму Крускала, відсортуємо усі ребра по неубиванію ваги. Потім помістимо
кожну вершину в своє дерево (тобто своє безліч) на це піде в сумі O (N). Перебираємо
усі ребра (у порядку сортування) і для кожного ребра за O (1) визначаємо, чи
належать його кінці різних деревам (за допомогою двох викликів FindSet за O
(1)). Нарешті, об"єднання двох дерев буде здійснюватися викликом Union - також
за O (1). Разом ми отримуємо асимптотики O (M log N + N + M) = O (M log N). void
kruskal() { int
k, i, p, q; pr_count=0; sr_count=0; q_sort(1,
m); //
сортируем список ребер по неубыванию for
(i = 0;i< n;i++) // цикл по вершинам { r[i]
= i; // у вершина своя компонента связности s[i]
= 0; // размер компоненты связности } k
= 0; // номер первого ребра + 1 for
(i = 0;i< n-1;i++) // цикл по ребрам mst { do {
// ищем ребра из разных k++;
// компонент связности p
= a[k].x; pr_count++; q
= a[k].y; pr_count++; while
(r[p]!=p) // ищем корень для p // { sr_count++; p
= r[p]; pr_count++; } while
(r[q]!=q) // ищем корень для q } { sr_count++; q
= r[q]; pr_count++; } }while
(p==q); printf("%d
%d
",a[k].x, a[k].y); // вывод ребра mst_weight+=a[k].w; if
(s[p] < s[q]) // взвешенное объединение {
// компоненты связности r[p]
= q; pr_count++; s[q]
= s[q] + s[p]; pr_count++; } else { r[q]
= p; pr_count++; s[p]
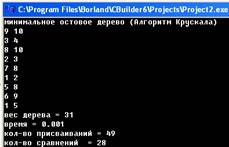
= s[p] + s[q]; pr_count++; } } } Результат
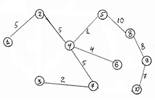
роботи програми: В
результаті виконання програм ми переконалися, що вони дають однакове мінімальне
остове дерево, яке має вигляд: Висновок.
Якщо кількість вершин достатньо мала, то доцільніше
використовувати алгоритм Прима, в іншому випадку доцільно користуватися
алгоритмом Крускала. Код
програм Алгоритм
Прима. #include
#include
#include
#include
const
int maxn = 100, inf = MAXINT/2, Max = 10000; int
a[maxn][maxn], p[maxn], z; int
v[maxn]; int
d[maxn], n, mst_weight, pr_count, sr_count; clock_t
start, end; void
init() { int
i, j, x, y, nn, z; FILE
*f; mst_weight
= 0; for
(i = 0;i for
(j = 0;j a[i][j]
= inf; for
(i =0;i< maxn; i++) { v[i]=0; d[i]=0; p[i]=0; } f=fopen("input.txt","rt"); fscanf(f,"%d",&n); fscanf(f,"%d",&nn); for
(i = 0;i< nn;i++) { fscanf(f,"%d
%d %d",&x, &y, &z); a[x-1][y-1]
= z; a[y-1][x-1]
= z; // если неориентированный граф } fclose(f); } void
prim() { } int
main() { clrscr(); init(); printf("Min
ostove derevo (by Prim)
"); start=
clock(); prim(); end=
clock(); printf("Vaga
dereva = %d
", mst_weight); printf("Time
= %f
", (end-start)/CLK_TCK); printf("Comparison
= %d
", pr_count); printf("Assignment
= %d
", sr_count); getch(); return
0; } //--------------------------------------------------------------------------- Алгоритм
Крускала. //--------------------------------------------------------------------------- #include
#pragma
hdrstop //--------------------------------------------------------------------------- #pragma
argsused //--------------------------------------------------------------------------- #include
#include
#include
#include
const
int maxn = 10, maxm = 1000, inf = MAXINT/2, Max = 10000; typedef
struct edge { int
x, y; // вершины ребра int
w; // вес ребра }eg; eg
a[maxm]; // список ребер int
s[maxn]; // размер компонент связности int
r[maxn]; // связи вершин в компонентах связности int
n, m; // кол-во вершин и ребер int
mst_weight; // вес минимального остовного дерева int
pr_count,sr_count; // кол-во присваиваний и сравнений //
инициализация и чтение данных void
init() { int
i, j, x, y, nn, z; FILE
*f; mst_weight
= 0; f=fopen("input.txt","rt"); fscanf(f,"%d",&n); fscanf(f,"%d",&m); for
(i = 0; i < m;i++) { fscanf(f,"%d
%d %d",&x, &y, &z); a[i].x
= x; a[i].y
= y; a[i].w
= z; } } void
q_sort(int l,int r) { int
i, j, x; i
= l; j
= r; x
= a[l+rand()%(r-l+1)].w; do { while
(i<=r && x > a[i].w) i++; while
(j>=x && x < a[j].w) j--; if
(i <= j) { if
(i { eg
buf; buf=a[i]; a[i]=a[j]; a[j]=buf; } i++; j--; } }
while (i <= j); if
(l < j) q_sort(l, j); if
(i < r) q_sort(i, r); } //
построение mst (алгоритм Крускала) void
kruskal() { } int
main(int argc, char* argv[]) { clrscr(); clock_t
start, end; init(); printf("Min
ostove derevo (by Kruskalo)
"); start=
clock(); kruskal(); end
= clock(); printf("Vaga
dereva = %d
", mst_weight); printf("Time
= %f
", (end-start)/CLK_TCK); printf("Comparison
= %d
", pr_count); printf("Assignment
= %d
", sr_count); getch(); return
0; } //--------------------------------------------------------------------------- Література 1. Кормен Т.,
Лейзенсон Ч., Ривест Р. Алгоритмы: построрение и анализ. - М. : МЦНМО, 2001. -
960 с. 2. Вікіпедия:
Алгоритм Прима 3. Вікіпедия:
Алгоритм Крускала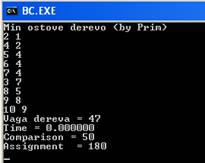














 (zip - application/zip)
(zip - application/zip)










