«САМАРСКИЙ ГОСУДАРСТВЕННЫЙ АЭРОКОСМИЧЕСКИЙ
УНИВЕРСИТЕТ имени академика С.П. КОРОЛЕВА
(национальный исследовательский университет)»
(СГАУ)

Факультет экономики и управления
Кафедра математических методов в экономике

КУРСОВАЯ РАБОТА
ПО КУРСУ «МАТЕМАТИЧЕСКАЯ ЭКОНОМИКА»
тема«Экономико-математическое моделирование фирмы (на примере производства мебели)»
Вариант №4

Выполнила:
студентка группы 737Захарова Н.В.
Проверил:
профессор Гераськин М.И.
Рецензент:
старший препод. Егорова В.В.

Самара 2016

РЕЦЕНЗИЯ
НА КУРСОВУЮ РАБОТУ
ПО КУРСУ «МАТЕМАТИЧЕСКАЯ ЭКОНОМИКА»
на тему «Экономико-математическое моделирование фирмы (на примере производства мебели)»,

выполненную студенткой группы 7307 Захаровой Н.В.

         В курсовой работе рассмотрены такие вопросы экономико-математического моделирования коммерческой деятельности производственной фирмы, как анализ производственного процесса, анализ и оптимизация издержек, анализ потребительских предпочтений и определение функций спроса, выбор оптимальной программы выпуска продукции.

         Работа выполнена на основе информации о корпорации

(______________________________________________________)

вид деятельности и наименование корпорации

         Работа выполнена

(______________________________________________________)

в полном объеме (частично), с высоким (низким) качеством, аккуратно (неаккуратно) оформлена

         Рекомендуется оценка

(______________________________________________________)

отлично (хорошо, удовлетворительно)

Рецензент
старший преподаватель
кафедры математических
методов в экономике                                                  Егорова В.В.

Оглавление

Введение. 4

1. Анализ производственного процесса корпорации. 5

1.1. Выбор рынка потребительского товара в сфере производства. 5

1.2.Построение производственных функций фирм. 6

1.3. Анализ экономико-математических характеристик производственных функций. 9

2.      Анализ и оптимизация издержек корпорации. 12

2.1. Анализ фактических издержек фирм. 12

2.2. Определение функций долгосрочных издержек фирм. 14

2.3. Линии долгосрочного развития. 15

2.4. Анализ предельных и средних издержек. 18

2.5. Анализ издержек в краткосрочном периоде. 20

 

Введение

Цель работы: освоение навыков экономико-математического моделирования коммерческой деятельности производственной фирмы на различных типах потребительских рынков.

Задачи работы:

– формирование экономико-математических моделей производственных процессов фирм в виде производственных функций;

– разработка моделей издержек производственных фирм в виде функций издержек;

– анализ тенденций развития потребительских рынков и определений функций потребительского спроса;

– разработка оптимизационных моделей коммерческой деятельности производственных фирм и определение оптимальной производственной программы на различных типах потребительских рынков;

– проверка условий равновесия производства и потребления.

1. Анализ производственного процесса корпорации.

1.1. Выбор рынка потребительского товара в сфере производства.

Рассматривается корпорация, включающая в себя две вертикально интегрированные фирмы: мебельная фабрика «Nobilia» и деревообрабатывающий завод  «Forest». Деревообрабатывающий завод занимается производством фанеры для мебели, в чем является монополистом в нескольких областях РФ. Мебельная фабрика производит различную мебель из дерева и является участником конкурентного рынка.Бизнес-процесс такой интеграции изображен на Рисунке 1.

 

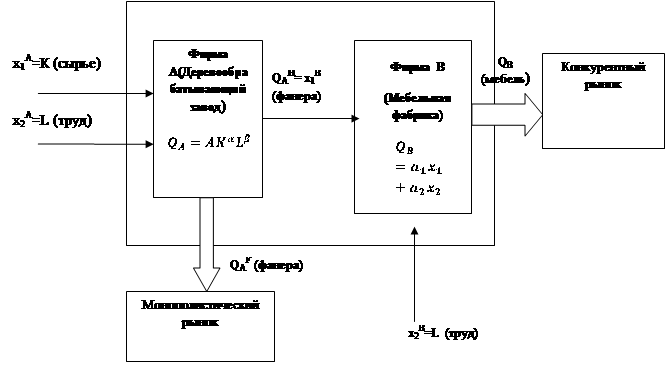
Рис. 1 – Схема вертикальной интеграции деревообрабатывающего завода и мебельной фабрики.

Представленный бизнес-процесс описывается следующим образом: деревообрабатывающий завод (фирма А) закупает сырье (х₁^А) и оплачивает труд рабочих(х₂^А), затем отправляет заготовки фанеры на монополистический в своем регионе рынок (Q_A^F), а также на дальнейшее производство (Q_A^H)- в мебельную фабрику (фирма B), где помимо заготовок фанеры в качестве ресурса также используется труд рабочих (х₂^В), а готовая продукция (Q_В) – деревянная мебель поступает на конкурентный рынок в различные магазины города.

1.2.Построение производственных функций фирм.

Для дальнейших расчетов потребуются данные об объемах производства и затрат ресурсов фирм. Эти данные представлены в Таблице 1.

Таблица 1 - Объемы производства и затрат ресурсов фирм.

Год	Фирма А			Фирма В
	х1 (К, ед.)	х2 (L, чел.)	Q (кв.км.)	х1(К, кв.км.)	х2 (L, чел.)	Q (шт.)
1	400	248	279,6	220,8	172	1129,6
2	800	256	340,4	265,6	184	1266,8
3	1200	264	385,6	296,8	196	1377,6
4	1600	272	423,6	322	208	1476
5	2000	280	457,6	343,2	220	1566,8

В таблице 1 указаны затраты каждого из ресурсов каждой фирмы и объемы выпуска изделий по годам. На основании данных этой таблицы построим кривые выпуска фирм (Рис. 2-3).

Рис. 2 – Кривая выпуска фирмы А (Q(x₁)).

Из графика, представленного на Рисунке 2 видно, что для фирмы А экономика описывается моделью Кобба-Дугласа, поэтому для расчетов будет применяться следующая формула:

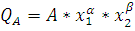
Рис. 3 – Кривая выпуска фирмы B (Q(x₁)).

Из графика, представленного на Рис.3 видно, что для фирмы В экономика описывается линейной моделью, поэтому для расчетов будет применяться следующая формула:

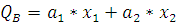
Для получения коэффициентов производственных функций фирм воспользуемся методом наименьших квадратов. Для этого построим вспомогательные таблицы.

Таблица 2 – Расчет суммы квадратов отклонения искомой функции для фирмы А.

С помощью встроенной функции Excel «Поиск решения» найдем коэффициенты производственной функции фирмы А. Для этого целевую ячейку (сумму квадратов отклонений) устремим к минимальному значению при изменении ячеек с предполагаемыми коэффициентами. При этом для производственной функции Кобба-Дугласа были получены следующие значения:

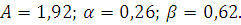При этом сама производственная функция примет вид:

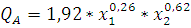
Таким же образом проведем расчеты коэффициентов производственной функции фирмы В. Построим вспомогательную таблицу с суммой квадратов отклонений.

Таблица 3 – Расчет суммы квадратов отклонения искомой функции для фирмы В.

Снова применяем встроенную функцию «Поиск решения» и получаем коэффициенты линейной производственной функции:

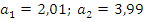
При этом сама производственная функция примет вид:

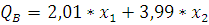
Рассчитаем объем выпуска для каждой фирмы на 6-ой год, если темп роста затрат ресурсов первой фирмы равен 1,2, а второй – 1,1.

Таблица 4 – Расчет объема выпуска фирмы А на 6-ой год.

Из таблицы 4 очевидно, что темп роста объема выпуска фирмы А меньше темпа роста затрат ресурсов:

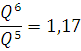
Это говорит о том, что для фирмы А характерен убывающий эффект от расширения масштаба, что так же подтверждается и полученными коэффициентами для функции Кобба-Дугласа, сумма которых меньше 1:

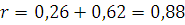
Проведем такой же расчет для фирмы В.

Таблица 5 – Расчет объема выпуска фирмы В на 6-ой год.

Из таблицы 5 видно, что темп роста объема выпуска продукции совпадает с темпом роста затрат ресурсов:

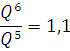
Это говорит о том, что для фирмы В характерен постоянный эффект от расширения масштаба.

1.3. Анализ экономико-математических характеристик производственных функций.

Произведем расчет средних и предельных продуктов для обеих фирм.

При затратах первого ресурса в размере 2000 ед. средняя производительность первой фирмы составит:

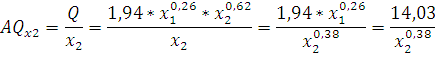
Из формулы видно, что затраты второго ресурса находятся в знаменателе, следовательно, с увеличением этих затрат средняя производительность будет снижаться.

Предельная производительность первой фирмы при затратах первого ресурса в размере 2000 ед. составит:

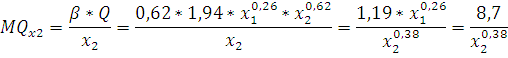
Из формулы видно, что с увеличением затрат второго ресурса предельный продукт уменьшается. В сравнении со средней производительностью, предельная производительность всегда будет меньше.

Эластичность по труду для первой фирмы  составит:

Построим сравнительные графики предельной и средней производительности первой фирмы и ее эластичности по труду (Рисунок 4).

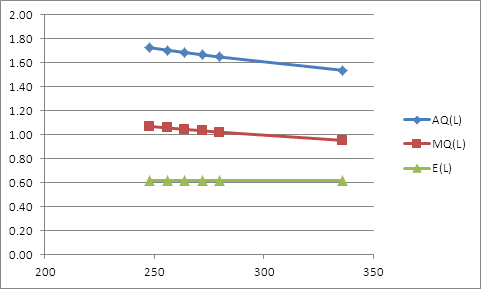
Рис. 4 – Средняя и предельная производительность первой фирмы.

Из графика видно, что предельная производительность всегда меньше средней и при этом стремится к значению коэффициента эластичности по труду. Это объясняется тем, что увеличение числа рабочих при неизменных затратах другого ресурса ведет к снижению производительности каждого из рабочих в отдельности. Коэффициент эластичности показывает степень участия ресурсов в производственном процессе и является асимптотой для графика предельной производительности.

Рассчитаем те же коэффициенты для второй фирмы. При неизменном значении первого ресурса в размере 343,2 ед. получим значение средней производительности:

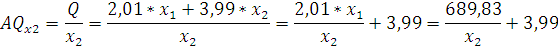
Из формулы видно, что затраты второго ресурса находятся в знаменателе, следовательно, с увеличением этих затрат средняя производительность будет снижаться.

Предельная производительность второй фирмы при постоянных затратах первого ресурса составит:

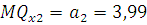
Из формулы видно, что предельная производительность второй фирмы не зависит от затрат ресурсов.

Коэффициент эластичности по труду для второй фирмы составит:

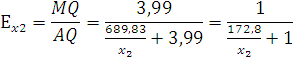
Из формулы видно, что с ростом затрат на ресурсы труда, коэффициент эластичности растет. Его максимальное значение будет равным 1.

Построим графики средней и предельной производительности и эластичности по труду для второй фирмы (Рисунок 5).

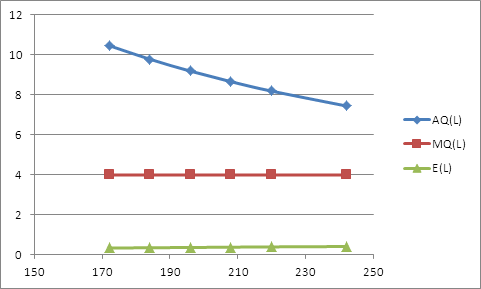
Рис. 5 - Средняя и предельная производительность второй фирмы.

Из графика видно, что предельная производительность является асимптотой для среднего продукта, а для коэффициента эластичности по труду асимптотой является значение, равное 1.

         Таким образом, из анализа графиков характеристик обеих фирм видно, что для 6-го года характерно резкое увеличение затрат труда, по сравнению с предыдущим годом, что приводит к более интенсивному уменьшению значений средних и предельных производительностей.

2.     Анализ и оптимизация издержек корпорации.

2.1. Анализ фактических издержек фирм.

Для расчета издержек фирм необходимо преобразовать таблицу затрат ресурсов в таблицу издержек. Известно, что ресурсы первой фирмы имеют следующие цены:

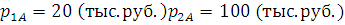
Цена второго ресурса второй фирмы:

Цену первого ресурса для второй фирмы определим через внутреннюю рентабельность:

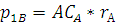
Средние издержки фирмы А рассчитаем по формуле:

Получаем таблицу издержек фирм (Таблица 6).

Таблица 6 – Издержки фирм.

По данным таблицы 6 построим графики издержек фирм (Рис. 6-7).

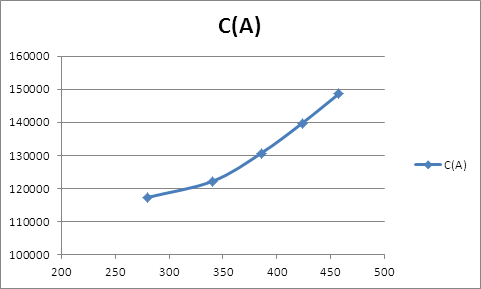
Рис. 6 –Фактические издержки фирмы А.

Из графика видно, что издержки фирмы А растут пропорционально объему выпуска, следовательно, можно сказать, что для фирмы А характерен постоянный эффект от расширения масштаба.

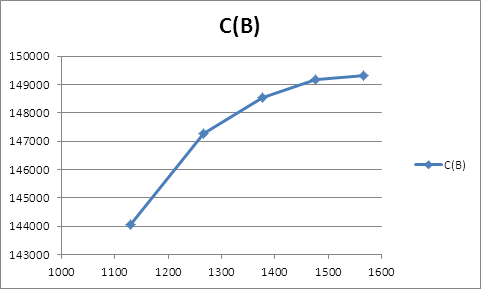
Рис. 7 –Фактические издержки фирмы В.

Из графика видно, что издержки фирмы В растут медленнее чем объем выпуска, что говорит об убывающем эффекте от расширения масштаба.

2.2. Определение функций долгосрочных издержек фирм.

Для определения функции долгосрочных издержек фирмы А, необходимо знать функции спроса на ресурсы:

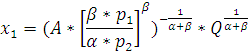
Тогда функция издержек примет вид:

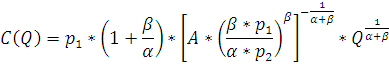
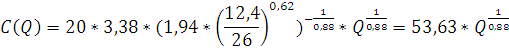
Построим сравнительный график фактических и расчетных издержек фирмы А (Рис. 8).

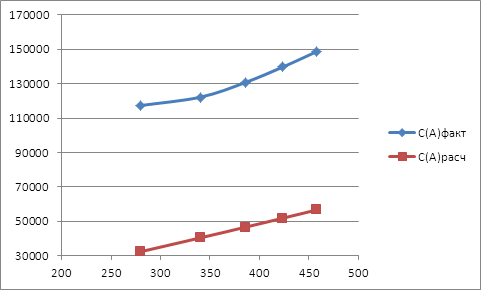
Рис. 8 – Расчетные и фактические издержки фирмы А.

Как видно из графика, фактические данные расходятся с расчетными. График оптимальных издержек проходит  ниже графика фактических издержек, что говорит о том, что у фирмы А есть резервы для снижения издержек.

Такой же график построим для фирмы В. Технология расчета теоретической функции издержек для нее будет представлена в пункте 2.3.

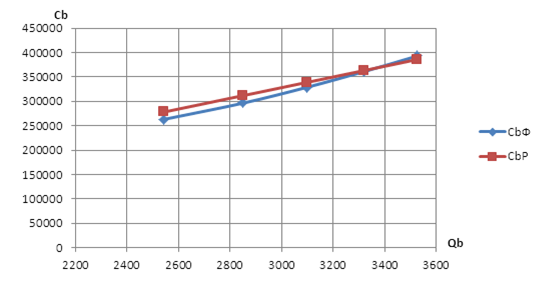
Рис. 9 - Расчетные и фактические издержки фирмы В.

Из графика видно, что фактические издержки фирмы В проходят очень близко к расчетным и даже чуть ниже, что говорит об оптимальном использовании ресурсов и распределении издержек. Несовпадение расчетной и фактической функций издержек обуславливается тем, что на практике фирма В использует второй ресурс, а в оптимальном плане второй ресурс полностью отсутствует.

2.3. Линии долгосрочного развития.

Для построения линий долгосрочного развития фирм, необходимо построить несколько изоквант и изокост, найти их точки касания и провести прямую, проходящую через эти точки касания. Запишем формулу изокванды для функции Кобба-Дугласа:

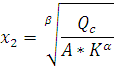
Формула изокосты имеет вид:

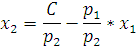
Для построения графика, возьмем значения объемов производства, затрат первого ресурса и издержек за 3, 4 и 5 года. В таблице 7 представлены расчеты, необходимые для графического представления.

Таблица 7 - Данные для построения изоквант и изокост фирмы А.

Выполнив построения, получаем график, представленный на рис. 10.

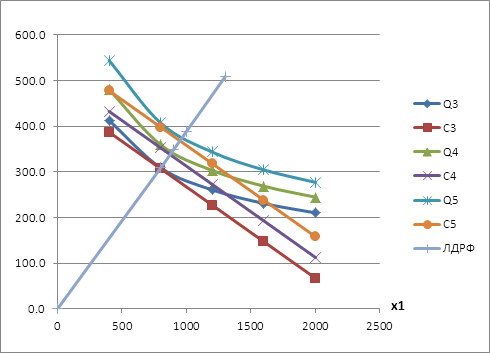
Рис. 10 - Линия долгосрочного развития фирмы А.

На графике видно, что линия долгосрочного развития проходит через точки касания изоквант и изокост и через начало координат. Эта линия показывает набор точек, при которых достигается минимум издержек производства, при различных объемах выпускаемой продукции.

Для построения линии долгосрочного развития фирмы В, необходимо построить 2 изокванты и изокосты, проходящие через точки, характеризующие использование только одного ресурса. Запишем формулу изокванты:

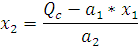
Формула изокосты имеет вид:

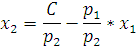
Поочередно приравниваем каждый из ресурсов к 0 и строим график (рис. 11).

Рис. 11 - линия долгосрочного развития фирмы В.

Из графика видно, что изокосты пересекают изокванты в точках А1 и А2, в которых значение второго ресурса равны 0. По этим точкам строим линию долгосрочного развития фирмы В, которая представляет собой горизонтальную прямую, совпадающую с осью координат. Таким образом, получаем и функцию издержек для фирмы В:

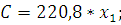
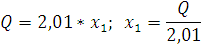
По этой формуле был построен график теоретических издержек фирмы В в пункте 2.2.

2.4. Анализ предельных и средних издержек.

Для анализа предельных и средних издержек фирмы А, необходимо построить их графики. Для расчета средних издержек функции Кобба-Дугласа, воспользуемся следующей формулой:

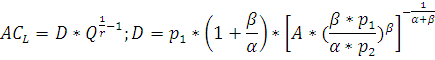
Формула предельных издержек имеет вид:

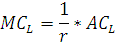
Построим график средних и предельных издержек фирмы А.

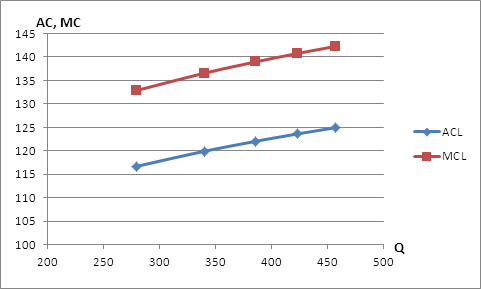
Рис. 12. - График средних и предельных издержек фирмы А.

Из графика видно, что и средние и предельные издержки фирмы А растут с увеличение объема производства, что обуславливается отрицательным эффектом от расширения масштаба. С экономической точки зрения возрастание предельных и средних издержек говорит о том, что каждая дополнительная единица продукции обходится фирме А дороже предыдущей.

Построим сравнительный график теоретических и фактических средних издержек формы А по годам (Рис. 13).

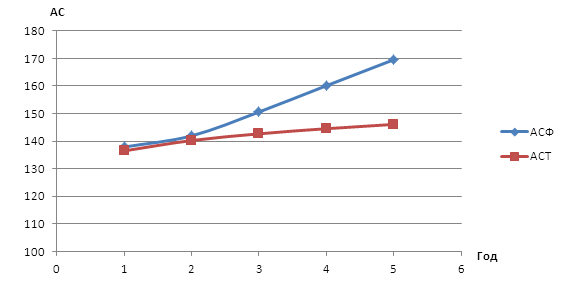
Рис. 13 - Теоретические и фактические средние издержки фирмы А.

Из графика видно, что теоретические средние издержки проходят ниже фактических, что говорит о том, что фактически ресурсы используются не оптимально, и у фирмы А еще есть резервы для снижения издержек.

Рассчитаем средние и предельные издержки для фирмы В.

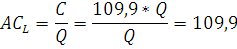
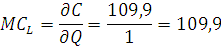
Как видно из расчетов, средние и предельные издержки фирмы В совпадают. Аналитически это обуславливается тем, что производственная функция представляет собой удельные средние издержки, зависящие только от объема выпуска продукции, поэтому объем выпуска сокращается в случае средних издержек и вовсе уходит в случае предельных при взятии производной.

2.5. Анализ издержек в краткосрочном периоде.

Особенностью краткосрочного периода является постоянство значений одного из ресурсов. В данном разделе примем за постоянный первый ресурс.

Общие издержки в краткосрочном периоде для фирмы А описываются формулой:

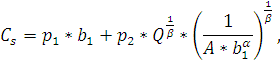
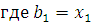
Построим график общих издержек фирмы А в краткосрочном периоде на графике фактических и теоретических издержек долгосрочного периода (Рис. 14).

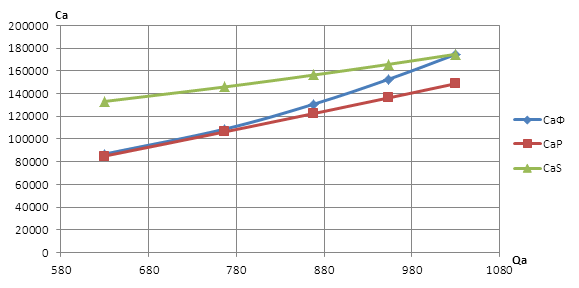
Рис. 14 - Сравнительный график краткосрочных и долгосрочных издержек фирмы А.

Из графика видно, что краткосрочные издержки проходят выше долгосрочных и пересекаются с фактическими издержками в значении пятого года. Такое поведение графика краткосрочных издержек обуславливается тем, что его начальная точка лежит выше оси абсцисс, в отличие от долгосрочных издержек, так как в краткосрочном периоде есть фиксированные издержки равные:

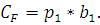
Произведем расчет средних и предельных издержек фирмы А в краткосрочном периоде. Формула средних издержек имеет вид:

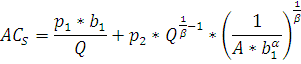
Предельные издержки рассчитаем по формуле:

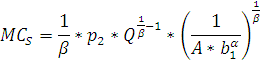
Построим график предельных и средних издержек фирмы А в краткосрочном периоде и сравним эти значения с издержками в долгосрочном периоде (Рис. 15).

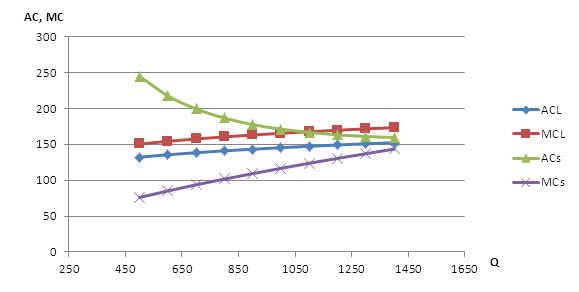
Рис. 15 - Сравнительный график краткосрочных и долгосрочных издержек фирмы А.

Из графика видно, что краткосрочные средние издержки лежат выше предельных. Средние и предельные издержки краткосрочного периода стремятся друг к другу. Такой вид графика обуславливается тем, что в краткосрочном периоде присутствуют фиксированные издержки, т. е. на каждую последующую единицу продукции средние фиксированные издержки значительно убывают, в то время как приращение издержек с каждой новой единицей продукции растет.

Краткосрочные предельные издержки лежат ниже долгосрочных. Это объясняется тем, что один ресурс остается постоянным в краткосрочном периоде, и его приращение с каждой новой единицей продукции равно 0, в то время как в долгосрочном периоде на приращение издержек влияют оба ресурса.