Министерство образования и науки РФ
Федеральное государственное бюджетное образовательное учреждение
высшего образования
«Уфимский государственный нефтяной технический университет»
Кафедра «Гидравлика и гидромашины»
Курсовая работа
«Гидравлический расчет сложного трубопровода
и элементов оборудования»
по дисциплине «Гидравлика и нефтегазовая гидромеханика»
Выполнил: студент гр. БМТ-14-05 ___________ Р.Р. Талхин
(подпись, дата)
Проверил: ___________ Е.Л. Артемьева
(подпись, дата)
Уфа 2016
1.
Выполнить
гидравлический расчет разветвленного трубопровода,  схема
которого прилагается. Определить
схема
которого прилагается. Определить 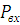 насоса,
насоса,
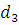 ,
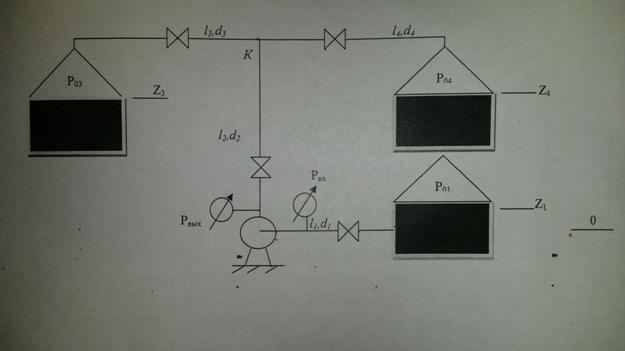
, из
условия, что
из
условия, что  .
.
Исходные данные:
Проектный
расход, м3/час ____Q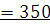 ________
________
Перекачиваемая жидкость ρ = 860 кг/м3; υ = 30*10-6 м2/c
Температура перекачки __________________________
Эквивалентная шероховатость_Кэ=0,02 мм___________
|
№ |
l, м |
d, мм |
zн, м |
zк, м |
pн, кПа |
pк, кПа |
Q, м3/ч |
Примечание |
|
1 |
100 |
275 |
Z1=2 |
ZВХ=0 |
P01= 100 |
Pвх-? |
350 |
|
|
2 |
200 |
250 |
ZВЫХ=0 |
ZK |
Pвых=1200 |
PK |
350 |
|
|
3 |
250 |
? |
ZK |
Z3=8 |
PK |
P03=100 |
? |
|
|
4 |
200 |
? |
ZK |
Z4=8 |
PK |
P04=100 |
? |
Данную схему можно разбить на 4 простых трубопровода, причем трубопровод l1d1 является всасывающим и рассчитывается отдельно от сложного трубопровода, состоящего из трубы 2 (l2d2), трубы 3 (l3d3) и трубы 4 (l4d4).
Составим уравнение Бернулли для трубопровода 1. При этом начальное сечение соответствует свободной поверхности жидкости в первом резервуаре, а конечное сечение – на входе в насос.
 (1)
(1)
где z1 – высотная отметка начального сечения;
р01 – избыточное давление на свободной поверхности в первом резервуаре;
Zвх – высотная отметка входа в насос;
рвх – избыточное давление на входе в насос;
Σh1 – суммарные потери напора в первом трубопроводе.
Данное уравнение позволит вычислить Pвх при известном расходе Q.
Рассчитаем потери напора в трубопроводе 1 по формуле Дарси-Вейсбаха:

Для данного значения Q рассчитаем число Рейнольдса:
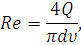
где d – диаметр трубопровода,
υ – кинематическая вязкость.
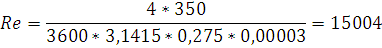
Находим граничные числа Рейнольдса:
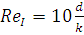 ,
,
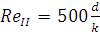
ReI=10*0,275/0.00002=137500
ReII=500*0,275/0.00002=6875000
Сравниваем
полученное
число Рейнольдса с критич ескимReкр
= 2320 и граничными числами:
ескимReкр
= 2320 и граничными числами:
2320< Re <137500<6875000.
Значит режим движения турбулентный, зона гладкого трения, и λ определяем по формуле Блазиуса:
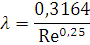
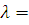 0,3164/
150040,25=0,028588
0,3164/
150040,25=0,028588
 Найдем
потери напора в трубопроводе 1:
Найдем
потери напора в трубопроводе 1:

Из
уравнения (1) найдем 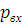 :
:
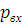 =
=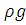 *(z1+p01/
*(z1+p01/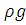 –zвх-Σh1
–zвх-Σh1 ;
;
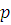 вх=860*9,81*(2+100000/(860*9,81)-0-1,42)=104886
Па
вх=860*9,81*(2+100000/(860*9,81)-0-1,42)=104886
Па
Составим систему уравнений Бернулли и уравнений расходов для разветвленной части трубопроводной сети.
Для трубопровода 2:
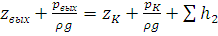 ,
,
Обозначая
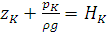 ,
преобразуем уравнение к виду:
,
преобразуем уравнение к виду:
Zвых+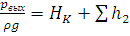 ,
,
или
 .
.
Для трубопровода 3:
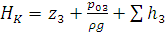 .
.
Для трубопровода 4:
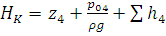 .
.
Потери напора в трубопроводе 2 найдем по формуле Дарси-Вейсбаха:

Рассчитаем число Рейнольдса:
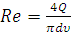 =
=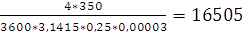
Сравниваем полученное число Рейнольдса с критическим Reкр = 2320 и граничными числами:
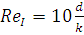 =
=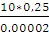 =125000
=125000
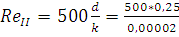 =6250000
=6250000
2320
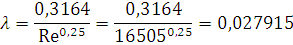
Находим h2:
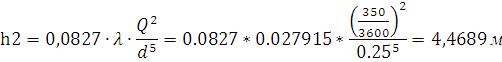
Из уравнения (2) находим 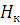 :
:
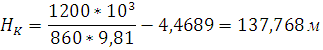
Уравнения расходов:
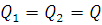
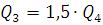
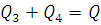
Полученные уравнения сведем в систему:
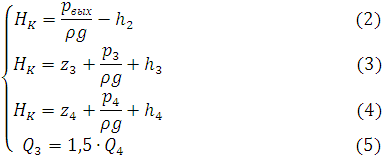
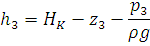
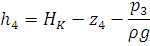
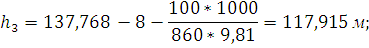
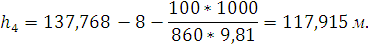
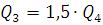
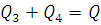
Следовательно
Q=1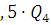 +
+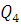 =2,5Q,
значит
=2,5Q,
значит 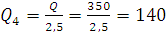 ,
,
а
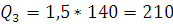
Зададимся значениями скоростей от 1 до 5 и рассчитаем диаметры и потери напора в трубопроводах 3, 4 по формуле Дарси-Вейсбаха:
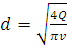 ;
;
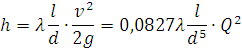
Для каждого значения расхода Q рассчитываем число Рейнольдса:
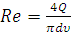 ,
,
Сравнивая
полученное число Рейнольдса с критическимReкр
= 2320 и граничными числами 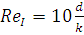 и
и
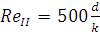 ,выбираем
формулу для расчета коэффициента гидравлического сопротивления λ:
,выбираем
формулу для расчета коэффициента гидравлического сопротивления λ:
Reкр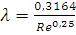 ;
;
Результаты вычислений сводим в таблицы:
Таблица 1 – Гидравлический расчет 3-го трубопровода
|
v, м/с |
h, м |
d, м |
Re |
Re1 |
Re2 |
Режим движения |
|
|
1 |
1,69 |
0,252 |
8425 |
126000 |
6426000 |
Турбулентный режим. Гладкое трения. |
0,033 |
|
1,05 |
1,89 |
0,246 |
8631 |
123000 |
6273000 |
0,0328 |
|
|
1,1 |
2,09 |
0,241 |
8810 |
120500 |
6145500 |
0,0327 |
|
|
1,15 |
2,35 |
0,235 |
9035 |
117500 |
5992500 |
0,0325 |
|
|
1,2 |
2,61 |
0,23 |
9231 |
115000 |
5865000 |
0,0323 |
|
|
1,25 |
2,83 |
0,226 |
9394 |
113000 |
5763000 |
0,0321 |
|
|
1,3 |
3,15 |
0,221 |
9607 |
110500 |
5635500 |
0,032 |
|
|
1,35 |
3,43 |
0,217 |
9784 |
108500 |
5533500 |
0,0318 |
|
|
1,4 |
3,75 |
0,213 |
9968 |
106500 |
5431500 |
0,0317 |
|
|
1,45 |
4,02 |
0,21 |
10110 |
105000 |
5355000 |
0,0316 |
|
|
1,5 |
4,39 |
0,206 |
10307 |
103000 |
5253000 |
0,0314 |
|
|
2 |
8,8 |
0,178 |
11928 |
89000 |
4539000 |
0,0303 |
|
|
2,5 |
14,59 |
0,16 |
13270 |
80000 |
4080000 |
0,0295 |
|
|
3 |
22,51 |
0,146 |
14542 |
73000 |
3723000 |
0,0288 |
|
|
3,5 |
32,72 |
0,135 |
15727 |
67500 |
3442500 |
0,0283 |
|
|
4 |
45,37 |
0,126 |
16850 |
63000 |
3213000 |
0,0278 |
|
|
4,5 |
59,51 |
0,119 |
17842 |
59500 |
3034500 |
0,0274 |
|
|
5 |
75,95 |
0,113 |
18789 |
56500 |
2881500 |
0,027 |
|
 Таблица
2 – Гидравлический расчет 4-го трубопровода
Таблица
2 – Гидравлический расчет 4-го трубопровода
|
v, м/с |
h, м |
d, м |
Re |
Re1 |
Re2 |
Режим движения |
|
|
1 |
1,73 |
0,206 |
6871,011 |
103000 |
5253000 |
Турбулентный режим. Гладкое трения. |
0,0348 |
|
1,05 |
1,94 |
0,201 |
7041,931 |
100500 |
5125500 |
0,0345 |
|
|
1,1 |
2,19 |
0,196 |
7221,572 |
98000 |
4998000 |
0,0343 |
|
|
1,15 |
2,41 |
0,192 |
7372,022 |
96000 |
4896000 |
0,0341 |
|
|
1,2 |
2,67 |
0,188 |
7528,873 |
94000 |
4794000 |
0,034 |
|
|
1,25 |
2,96 |
0,184 |
7692,544 |
92000 |
4692000 |
0,0338 |
|
|
1,3 |
3,19 |
0,181 |
7820,045 |
90500 |
4615500 |
0,0336 |
|
|
1,35 |
3,56 |
0,177 |
7996,769 |
88500 |
4513500 |
0,0335 |
|
|
1,4 |
3,85 |
0,174 |
8134,645 |
87000 |
4437000 |
0,0333 |
|
|
1,45 |
4,19 |
0,171 |
8277,358 |
85500 |
4360500 |
0,0332 |
|
|
1,5 |
4,55 |
0,168 |
8425,168 |
84000 |
4284000 |
0,033 |
|
|
2 |
8,87 |
0,146 |
9694,713 |
73000 |
3723000 |
0,0319 |
|
|
2,5 |
15,39 |
0,13 |
10887,91 |
65000 |
3315000 |
0,031 |
|
|
3 |
23,41 |
0,119 |
11894,35 |
59500 |
3034500 |
0,0303 |
|
|
3,5 |
33,99 |
0,11 |
12867,53 |
55000 |
2805000 |
0,0297 |
|
|
4 |
46,42 |
0,103 |
13742,02 |
51500 |
2626500 |
0,0292 |
|
|
4,5 |
61,8 |
0,097 |
14592,04 |
48500 |
2473500 |
0,0288 |
|
|
5 |
79,39 |
0,092 |
15385,09 |
46000 |
2346000 |
0,0284 |
Построим график уравнений (3), (4) в координатах h-d.
Рисунок 1 – График зависимости потерь напора от диаметра для трубопровода 3.
|
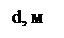
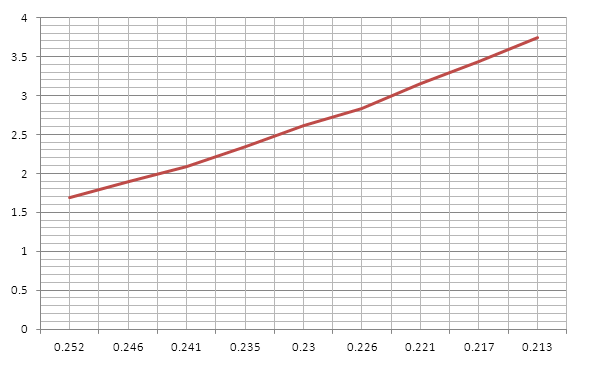
Рисунок 2 – График зависимости потерь напора от диаметра для трубопровода 4.
|

 По
графику находим: d3=0,225
м; d4=0,185
м.
По
графику находим: d3=0,225
м; d4=0,185
м.
Вывод: выполнен гидравлический расчет разветвленного трубопровода, схема которого прилагается. Определены искомые параметры:
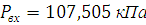 ;
;
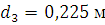 ;
;
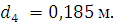
2. Как
изменятся  расходы
при изменении вязкости в 1,5 раз?
расходы
при изменении вязкости в 1,5 раз?
Решение:
Разбиваем сложный трубопровод на простые и записываем для каждого уравнение Бернулли, как в задании 2:
1:
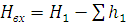 , (3.1)
, (3.1)
2:
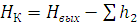 , (3.2)
, (3.2)
3:
 ,
(3.3)
,
(3.3)
4:
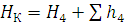 .
.
(3.4)
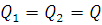 ,
,
 ,
,
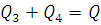 (3.5)
(3.5)
При
изменении вязкости с 30*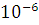 до
45*
до
45*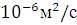 ,
изменятся числа Re, и ,возможно,
режим движения и зона трения. Граничные числа
,
изменятся числа Re, и ,возможно,
режим движения и зона трения. Граничные числа 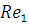 и
и
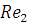 для
всех трубопроводов остались прежними (задание 2).
для
всех трубопроводов остались прежними (задание 2).
Составим гидравлические характеристики четырех трубопроводов, с учетом зоны трения и расчета коэффициента гидравлических сопротивлений по соответствующим формулам:
Гидравлическая характеристика для трубопровода 1:
|
Q , м3/ч |
Q, м3/с |
V, м/с2 |
Re |
|
h, м |
|
100 |
0,027778 |
0,47 |
2859,4508 |
0,0432679 |
0,18 |
|
150 |
0,041667 |
0,7 |
4289,1763 |
0,03909696 |
0,36 |
|
200 |
0,055556 |
0,94 |
5718,9017 |
0,03638382 |
0,6 |
|
250 |
0,069444 |
1,17 |
7148,6271 |
0,03440969 |
0,88 |
|
300 |
0,083333 |
1,4 |
8578,3525 |
0,03287649 |
1,22 |
|
350 |
0,097222 |
1,64 |
10008,078 |
0,03163361 |
1,59 |
|
400 |
0,111111 |
1,87 |
11437,803 |
0,03059503 |
2,01 |
|
450 |
0,125 |
2,11 |
12867,529 |
0,02970727 |
2,47 |
|
500 |
0,138889 |
2,34 |
14297,254 |
0,02893499 |
2,98 |
|
550 |
0,152778 |
2,57 |
15726,98 |
0,02825369 |
3,52 |
|
600 |
0,166667 |
2,81 |
17156,705 |
0,02764573 |
4,1 |
|
650 |
0,180556 |
3,04 |
18586,43 |
0,02709801 |
4,72 |
|
700 |
0,194444 |
3,28 |
20016,156 |
0,02660059 |
5,37 |
Гидравлическая характеристика для трубопровода 2:
|
Q, м3/ч |
Q, м3/c |
v, м/c |
Re |
|
h, м |
Hk, м |
|
100 |
0,027778 |
0,57 |
3145,396 |
0,042249 |
0,55 |
25,83 |
|
150 |
0,041667 |
0,85 |
4718,094 |
0,038176 |
1,13 |
25,25 |
|
200 |
0,055556 |
1,13 |
6290,792 |
0,035527 |
1,87 |
24,51 |
|
250 |
0,069444 |
1,42 |
7863,49 |
0,033599 |
2,76 |
23,62 |
|
300 |
0,083333 |
1,7 |
9436,188 |
0,032102 |
3,8 |
22,58 |
|
350 |
0,097222 |
1,98 |
11008,89 |
0,030889 |
4,98 |
21,4 |
|
400 |
0,111111 |
2,26 |
12581,58 |
0,029875 |
6,29 |
20,09 |
|
450 |
0,125 |
2,55 |
14154,28 |
0,029008 |
7,73 |
18,65 |
|
500 |
0,138889 |
2,83 |
15726,98 |
0,028254 |
9,29 |
17,09 |
|
550 |
0,152778 |
3,11 |
17299,68 |
0,027588 |
10,98 |
15,4 |
|
600 |
0,166667 |
3,4 |
18872,38 |
0,026995 |
12,79 |
13,59 |
|
650 |
0,180556 |
3,68 |
20445,07 |
0,02646 |
14,72 |
11,66 |
|
700 |
0,194444 |
3,96 |
22017,77 |
0,025974 |
16,76 |
9,62 |
 |
Гидравлическая характеристика для трубопровода 3:
|
Q, м3/ч |
Q, м3/c |
v, м/c |
Re |
|
h, м |
Hk, м |
|
0 |
0 |
0 |
0 |
0 |
0 |
19,993 |
|
50 |
0,013889 |
0,35 |
1747,442 |
0,048937 |
0,34 |
20,333 |
|
100 |
0,027778 |
0,7 |
3494,884 |
0,041151 |
1,14 |
21,133 |
|
150 |
0,041667 |
1,05 |
5242,327 |
0,037184 |
2,32 |
22,313 |
|
200 |
0,055556 |
1,4 |
6989,769 |
0,034604 |
3,84 |
23,833 |
|
250 |
0,069444 |
1,75 |
8737,211 |
0,032726 |
5,68 |
25,673 |
|
300 |
0,083333 |
2,1 |
10484,65 |
0,031268 |
7,82 |
27,813 |
|
350 |
0,097222 |
2,45 |
12232,1 |
0,030086 |
10,24 |
30,233 |
|
400 |
0,111111 |
2,8 |
13979,54 |
0,029098 |
12,94 |
32,933 |
|
450 |
0,125 |
3,15 |
15726,98 |
0,028254 |
15,91 |
35,903 |
|
500 |
0,138889 |
3,49 |
17474,42 |
0,027519 |
19,13 |
39,123 |
|
550 |
0,152778 |
3,84 |
19221,86 |
0,026871 |
22,6 |
42,593 |
|
600 |
0,166667 |
4,19 |
20969,31 |
0,026293 |
26,32 |
46,313 |
 Гидравлическая
характеристика для трубопровода 4:
Гидравлическая
характеристика для трубопровода 4:
|
Q, м3/ч |
Q, м3/c |
v, м/c |
Re |
|
h, м |
Hk, м |
|
0 |
0 |
0 |
0 |
0 |
0 |
19,993 |
|
50 |
0,013889 |
0,52 |
2125,268 |
0,0466 |
0,69 |
20,683 |
|
100 |
0,027778 |
1,03 |
4250,535 |
0,039186 |
2,32 |
22,313 |
|
150 |
0,041667 |
1,55 |
6375,803 |
0,035408 |
4,71 |
24,703 |
|
200 |
0,055556 |
2,07 |
8501,07 |
0,032951 |
7,8 |
27,793 |
|
250 |
0,069444 |
2,58 |
10626,34 |
0,031163 |
11,52 |
31,513 |
|
300 |
0,083333 |
3,1 |
12751,61 |
0,029775 |
15,86 |
35,853 |
|
350 |
0,097222 |
3,62 |
14876,87 |
0,028649 |
20,77 |
40,763 |
|
400 |
0,111111 |
4,14 |
17002,14 |
0,027708 |
26,24 |
46,233 |
|
450 |
0,125 |
4,65 |
19127,41 |
0,026904 |
32,26 |
52,253 |
|
500 |
0,138889 |
5,17 |
21252,68 |
0,026205 |
38,79 |
58,783 |
|
550 |
0,152778 |
5,69 |
23377,94 |
0,025588 |
45,84 |
65,833 |
|
600 |
0,166667 |
6,2 |
25503,21 |
0,025037 |
53,38 |
73,373 |
Для
трубопроводов при расходах от 100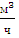 до
600
до
600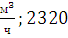 <
< <
<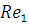 ,
режим движения турбулентный, зона гладкого трения. Коэффициент гидравлического
сопротивления вычисляем по формуле Блазиуса:
,
режим движения турбулентный, зона гладкого трения. Коэффициент гидравлического
сопротивления вычисляем по формуле Блазиуса:
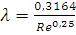 .
.
По уравнениям (3.2) – (3.5) строим графическую зависимость потерь от расхода:
|
|
|
|
|
|

Итак, при увеличении вязкости в 1,5 раза, расходы будут иметь значения:

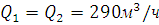 ;
;
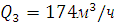 .
.

 Список
литературы
Список
литературы
1. Сборник задач по машиностроительной гидравлике: Учеб.пособие для машиностроительных вузов / Д.А. Бутаев, З.А. Калмыкова, Л.Г. Подвизда и др.; Под ред. И.И. Куколевского, Л.Г. Подвизда. – 5-е изд., стереотипное. – М.: Изд-во МГТУ им. Н.Э. Баумана, 2002. – 448с., ил.
2. Гидромеханика: учеб.пособие по решению задач / Л. Н. Раинкина - М.: Нефть и газ РГУ нефти и газа им. И.М. Губкина, 2005. - 131 с.














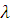
 (zip - application/zip)
(zip - application/zip)










