Оглавление

Введение. 4

Глава 1. 5

1.1.       Вычислительные методы. 5

1.2.       Численные метода интегрирования функций. 6

1.3.       Численные методы дифференцирования. 8

Введение

Что же такое вычислительная математика? Вычислительная математика-это такой раздел математики, в котором изучаются методы решения математических задач на компьютере. Эта наука зародилась из-за огромной необходимости решать разные практические задачи, вычисление которых вручную заняло бы очень много сил и времени.

Многие известные учёные такие как Эйлер, Якоби, Лагранж и другие  занимались задачами вычислительной математики. Из-за того, что им часто приходилось заниматься довольно сложными вычислениями на бумаге вручную, они невольно заложили основы науки.

Глава 1.

1.1.        Вычислительные методы.

Вычислительные (они же численные) методы – это методы приближённого решения задач прикладной математики в численном виде, основанный на реализации алгоритмов.

Существует два класса численных методов:

·        Прямые методы, которые за определённое количество операций позволяют найти решение задачи;

·        Итерационные методы, основанные на использовании циклического процесса и позволяющие получить решение путём последовательных приближений;

Решения, полученные при использовании численных методов, могут содержать погрешности.

Погрешности бывают следующих типов:

·        Абсолютная погрешность;

·        Относительная погрешность;

·        Предельная относительная погрешность;

·        Предельная абсолютная погрешность;

Абсолютной погрешностью называется разность числом и его точным значением.

Относительной погрешностью называется отношение абсолютной погрешности числа к самому числу.

Число, превышающее или равное абсолютной погрешности, называется предельной погрешностью. А предельной относительной погрешностью называется число, превышающее или равное относительной погрешности.

1.2.        Численные метода интегрирования функций

Численное интегрирование – это вычисление приближённого значения определённого интеграла.

Численное интегрирование применяется в двух случаях:

1.     Когда подынтегральная функция не задана аналитически;

2.     Когда аналитически задана, но первообразная не выражается через аналитические функции;

Существует множество методов интегрирования функций:

·        Метод прямоугольников;

·        Метод трапеций;

·        Метод парабол;

·        Метод Гаусса;

·        Метод Чебышева и многие другие;

Основная идея численного интегрирования состоит в замене подынтегральной функции на более простую, интеграл от которой легко вычисляется аналитически. Рассмотрим один из методов – метод прямоугольников.

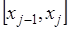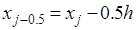Метод прямоугольников является одним из простейших методов численного интегрирования. На частичном отрезке   заменяют подынтегральную функцию полиномом Лагранжа нулевого порядка, построенным в одной точке. Естественно, что в качестве этой точки выбирается средняя  . Тогда значение интеграла на частичном отрезке:

               

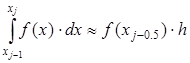
Получим формулу средних прямоугольников:

         

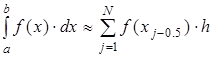
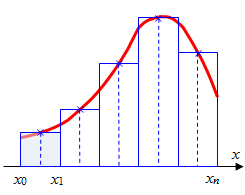
Рис.1.2.1. Средние прямоугольники

Из рисунка видно, что площадь криволинейной трапеции приближенно меняется многоугольника, составленного из N прямоугольников. Таким образом, вычисление определённого интеграла сводится к нахождению суммы N элементарных прямоугольников.

Формулу средних прямоугольников можно представить и в другом виде:

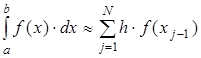 или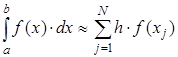      

Эти формулы называются формулой левых и правых прямоугольников.

Графически методы левых и правых прямоугольников представлен на рисунках. Однако из-за нарушения симметрии в формулах правых и левых прямоугольников, их погрешность значительно больше, чем в методе средних прямоугольников.

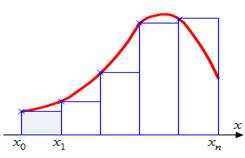
Рис.1.2.2. Левые прямоугольники

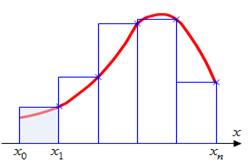
Рис.1.2.3. Правые прямоугольники

1.3.        Численные методы дифференцирования

Численное дифференцирование – это совокупность методов вычисления значения производной дискретно заданной функции. Основой численного дифференцирования является аппроксимация функции, от которой берётся производная.

Аппроксимацией называется метод, состоящий в замене одних объектов другими, в каком то смысле близкими, но более простыми.

Аппроксимация позволяет исследовать числовые характеристики и качественные свойства объекта, сводя задачу к изучению более простых, более удобных объектов.

.    

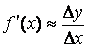Это соотношение называется аппроксимацией производной с помощью конечных разностей.

Соотношение может быть использовано для приближённого вычисления производной функции, заданной как аналитическим выражением, так и таблично. В первом случае выбор величины 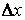произволен и определяется характером поведения функции. Для получения хорошей точности величину 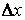выбирают достаточно малой, такой чтобы на интервале   функция 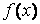 была бы монотонной и менялась несущественно. Если, функция задана таблично, величина 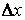 равна разности между соседними узлами таблицы в окрестности которых вычисляется производная. При этом, если количество узлов невелико и узлы расположены на большом расстоянии друг от друга формула 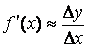 может давать существенную погрешность.

Интерполяционные полиномы.

Пусть в точках 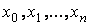 известны значения функции  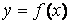: 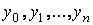. По табличным данным аппроксимируем функцию 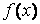  интерполяционным полином в степени n:

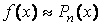
Тогда для k-той производной от функции 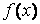 на отрезке интерполирования  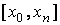получим приближенную формулу

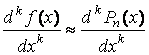
На практике редко прибегают к аппроксимации функции одним интерполяционным полиномом, т.е к глобальной интерполяции, в основном из-за свойственной для неё большой погрешности. В основном используется локальная интерполяция. При этом в окрестности точки, в которой нужно вычислить производную, функцию интерполируют полиномом невысокой степени.

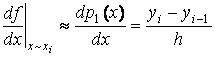  - формула левых разностей

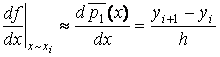 - формула правых разностей

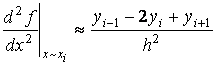 - формула средних разностей

Если необходимо вычислить производную по всем известным направлениям, то используется интерполяционный многочлен Ньютона.