Лабораторна
робота № 2![]()
ВИЗНАЧЕННЯ МОДУЛЯ ПРУЖНОСТІ
З ДЕФОРМАЦІЇ РОЗТЯГУ
Мета роботи: Дослідити залежність видовження зразка від навантаження. Визначити модуль Юнга для капрону.
Прилади і матеріали: Прилад для визначення модуля пружності, рулетка, мікрометр, важки.
Теоретичні відомості
Деформацією називають зміну форми чи об^єму твердого тіла, яка викликана дією зовнішніх сил. Якщо ці сили малі, то після припинення їх дії деформація зникає; якщо ж сили великі, то після припинення дії виявляється так звана залишкова деформація. При появі щонайменшої залишкової деформації говорять, що досягнуто межу пружності.
Оскільки результат дії сили залежить також і від розмірів зразка, то зручно дію сили оцінювати по напрузі, що виникає в зразку.
Напругою називають відношення сили F до площі поперечного перерізу зразка S:
|
|
(1) |
Таким чином, межа пружності sпр – це напруга, при якій з^являється залишкова деформація. Тіла з великим значенням sпр називають пружними, а тіла з дуже малим значенням sпр – непружними або пластичними.
Серед різних деформацій виділяють дві найпростіші: деформацію розтягу (стиску) і деформацію зсуву. Всі малі деформації можна розглядати як суму деяких розтягів (чи стисків) і зсувів.
Малі деформації задовольняють таким основним законам:
- в межах пружності деформація пропорційна прикладеній напрузі;
- при зміні напряму дії зовнішньої сили змінюється тільки напрям деформації без зміни її значення;
- при дії декількох зовнішніх сил загальна деформація дорівнює сумі окремих деформацій (принцип суперпозиції малих деформацій).
Для малих деформацій розтягу чи стиску стержня справедливий закон Гука:
|
|
(2) |
|
або
|
(2´) |
В (2) і (2´): l0 – початкова довжина стержня;
Dl=l–l0 – його абсолютне видовження;
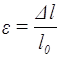 називають відносним
видовженням; a – коефіцієнт пружності під час
розтягу.
називають відносним
видовженням; a – коефіцієнт пружності під час
розтягу.
Величина, обернена a, називається модулем пружності під час розтягу, або модулем Юнга:
|
|
(3) |
З використанням модуля Юнга закон Гука записують так:
|
|
(4) |
Під дією сили F, що розтягує стержень, змінюються не тільки повздовжні, а й поперечні розміри стержня; говорять, що під час розтягу стержень зазнає поперечного стиску. Якщо d0 – діаметр стержня до деформації, d – після деформації, то
|
|
(5) |
де Dd = d – d0, b – коефіцієнт поперечного стиску.
Відношення
відносного поперечного стиску до відповідного відносного поздовжнього
видовження (або відношення ![]() )
називають коефіцієнтом Пуассона:
)
називають коефіцієнтом Пуассона: 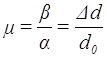 :
:![]() .
.
Теоретично для всіх ізотропних тіл m =0,25.
Опис установки
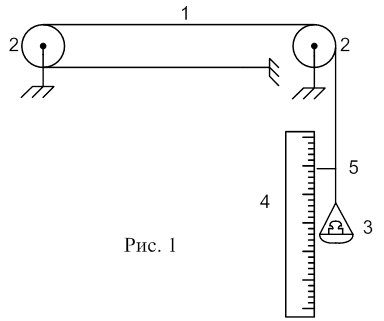
В установці (рис.1) використовується довга (близько 5 м) капронова нитка діаметром 0,2¸0,4 мм (рибальська волосінь). На малюнку вона позначена цифрою 1. За допомогою блоків 2 капронова нитка закріплена на робочому столі. До кінця нитки приєднано платформу для важків 3. Поруч вертикально закріплено лінійку 4, на якій з допомогою покажчика 5 можна відмічати положення кінця нитки. Значна довжина нитки дає змогу вже при невеликих навантаженнях (»1Н) з достатньою точністю виміряти абсолютне видовження Dl. Модуль Юнга визначається за формулою (3) для різних значень F.
Хід роботи
1. Виміряйте рулеткою довжину капронової нитки l0 до стрілки–покажчика 5 при ненавантаженій платформі. Допустима похибка вимірювання - 1 см.
2. Мікрометром виміряйте діаметр нитки d. Вимірювання виконайте декілька разів в різних місцях і знайдіть з одержаних значень середнє арифметичне.
3. Запишіть початкове положення стрілки–покажчика n0.
4. Навантажте платформу важком
масою m. При обчисленні сили тяжіння F, що діє на цей важок, g брати
рівним 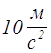 .
.
5. Запишіть положення стрілки n1.
6. Навантажуйте платформу послідовно важками, збільшуючи масу їх щоразу на m г. Записуйте кожного разу покази стрілки n2, n3, і т.д.
7. Максимальне навантаження уточніть у викладача.
8. Почніть розвантажувати платформу, знімаючи кожного разу теж по m г. Записуйте щоразу покази стрілки n¢6 , n¢5 , n¢4 і т.д. до n0.
9. Побудуйте графік зміни видовження нитки зі зміною навантаження F : при F1 Dl1 = n1 – n0
при F2 Dl2 = n2 – n0 і т.д.
10.Проаналізуйте одержаний графік. Чи виконується закон Гука?
11.Обчисліть для кожного видовження модуль Юнга за формулою:
|
|
(6) |
В (6) враховано,
що площа 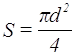 .
.
12.Знайдіть середнє арифметичне з одержаних значень Е і порівняйте з табличним.
13.Результати вимірювань і
обчислень можна подати у вигляді таблиці 1. Похибка вимірювань: ![]()
14.Кінцевий результат подати у
виді ![]() ,
,
де 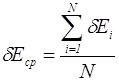 .
.
Табл.1
|
№ п/п |
F = mg, Н |
l0 , м |
d, м |
Dl, м |
E,
|
dE |
|
1 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
Середнє |
– |
|
|
– |
|
|
Контрольні запитання
1. Які деформації називають пружними?
2. Сформулюйте закон Гука.
3. Який фізичний зміст модуля Юнга?
4. Що називають коефіцієнтом Пуассона?
5. Накресліть діаграму розтягу дроту і поясніть фізичний смисл окремих її ділянок.
6. Яку довжину повинен мати мідний дріт, щоб він, якщо його підвісити вертикально, розірвався під дією власної ваги?














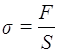
 ,
,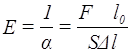
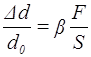 ,
,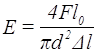
 (zip - application/zip)
(zip - application/zip)











