Виды распределения случайный величин

Министерство образование республики Башкортостана.

           ГАОУ СПО Стерлитамакский колледж строительства, экономики и права.

                                                                                
                                Специальность         230115

“Программирование в компьютерных системах”

        Реферат

по теме:  " Виды распределения

 случайный величин"

Выполнил: студент

гр. ПО-21

Зебров Н.В.

Проверила:

Долгих Е.А.

Оценка:___________

                                                           2012 г.

Случайные величины и законы распределения

Переменная величина называется случайной, если в результате опыта она может принимать действительные значения с определёнными вероятностями. Наиболее полной, исчерпывающей характеристикой случайной величины является закон распределения. Закон распределения – функция (таблица, график, формула), позволяющая определять вероятность того, что случайная величина  Х  принимает определенное значение хi  или попадает в некоторый интервал. Если случайная величина  имеет данный закон распределения, то говорят, что она распределена по этому закону или подчиняется этому закону распределения.

Случайная величина Х называется дискретной, если существует такая неотрицательная функция

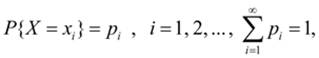
которая ставит в соответствие значению хi  переменной  Х  вероятность  рi  , с которой она принимает это значение.

Случайная величина  Х  называется  непрерывной, если для любых   a < b  существует такая неотрицательная функция  f ( x ), что

Функция  f ( x ) называется плотностью распределения непрерывной случайной величины.

Вероятность того, что случайная величина  Х  (дискретная или непрерывная) принимает значение, меньшее  х , называется функцией распределения случайной величины Х  и обозначается  F ( x ) :

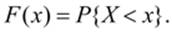
Функция распределения является универсальным видом закона распределения, пригодным для любой случайной величины.

Общие свойства функции распределения:

Кроме этого универсального, существуют также частные виды законов распределения:  ряд распределения 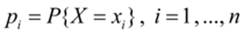 (только для дискретных случайных величин) и плотность распределения 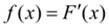(только для непрерывных случайных величин).

Основные свойства плотности распределения:

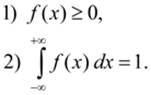
Каждый закон распределения – это некоторая функция, полностью описывающая случайную величину с вероятностной точки зрения. На практике о распределении вероятностей случайной величины Х  часто приходится судить только по результатам испытаний. Повторяя испытания, будем каждый раз регистрировать, произошло ли интересующее нас случайное событие А, или нет. Относительной частотой (или просто частотой) случайного события А называется отношение числа nA появлений этого события к общему числу n проведенных испытаний. При этом мы принимаем, что относительные частоты случайных событий близки к их вероятностям. Это тем более верно, чем больше число проведенных опытов. При этом частоты, как и вероятности, следует относить не к отдельным значениям случайной величины, а к интервалам. Это значит, что весь диапазон возможных значений случайной величины Х  надо разбить на интервалы. Проводя серии испытаний, дающих эмпирические значения величины Х , надо фиксировать числа nx попаданий результатов в каждый интервал. При большом числе испытаний n отношение nx  / n (частоты попадания в интервалы) должны быть близки к вероятностям попадания в эти интервалы. Зависимость частот nx  / n от интервалов определяет эмпирическое распределение вероятностей случайной величины Х, графическое представление которой называется гистограммой (рис. 1).

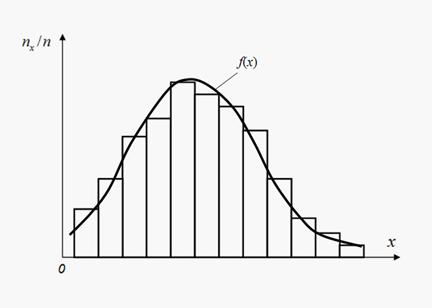
Рис. 1. Гистограмма и выравнивающая плотность распределения

 Для построения гистограммы по оси абсцисс откладывают интервалы равной длины, на которые разбивается весь диапазон возможных значений случайной величины Х , а по оси ординат откладывают частоты nx / n. Тогда высота каждого столбика гистограммы равна соответствующей частоте. Таким образом, получается приближенное представление закона распределения вероятностей для случайной величины Х в виде ступенчатой функции, аппроксимация (выравнивание) которой некоторой кривой f (x) даст плотность распределения.

Однако, часто бывает достаточно указать только отдельные числовые параметры, характеризующие основные свойства распределения. Эти числа называются числовыми характеристиками случайной величины.

Законом распределения случайной величины называется всякое соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями.

Закон распределения прерывной случайной величины Х может быть задан в следующих формах:

 • табличной;

 • аналитической;

 • графической.

Простейшей формой задания закона распределения прерывной случайной величины Х является таблица.

xi         x1        x2        …        xn

pi         p1        p2        …        pn

Такую таблицу называют рядом распределения случайной величины Х.

Чтобы придать ряду распределения более наглядный вид, часто прибегают к его графическому изображению.

Для непрерывной случайной величины такой характеристики построить нельзя!!!

Для непрерывной случайной величины удобно воспользоваться не вероятностью события Х=х, а вероятностью события Х<х, где х – некоторая текущая переменная. Вероятность этого события, очевидно, зависит от х и есть некоторая функция от х.

 Эта функция называется функцией распределения случайной величины Х и обозначается F(х):

                                                      F(x) = P(X< x)

Функцию распределения F(x) называют также интегральной функцией распределения или интегральным законом распределения.

Функция распределения полностью характеризует случайную величину с вероятностной точки зрения, т.е. является одной из форм закона распределения.

Сформулируем некоторые общие свойства функции распределения:

 1.F(x) – неубывающая функция своего аргумента т.е. при x2 > x1 F(x2) > F(x1);

 2. F(–∞) = 0;

 3. F(+∞) = 1.

Литература

http://all4study.ru/matematika/sluchajnye-velichiny-i-zakony-ix-raspredeleniya.html

http://www.coolreferat.com/Законы_распределения_случайных_величин_и_их_применение