Виды компьютерной графики

Федеральное государственное автономное

образовательное учреждение

высшего профессионального образования

«СИБИРСКИЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ»

_______________________ИАиД_______________________

институт

_________________________________________________________________

кафедра

РЕФЕРАТ

по __________________________________________________

наименование дисциплины

Виды компьютерной графики. Теория цвета.

Преподаватель                         __________             _______________

                                                              подпись, дата                           инициалы, фамилия

         Студент ____________ ________________   __________  _____________

                                      номер группы        номер зачетной книжки         подпись, дата      инициалы, фамилия

Красноярск 2012

Содержание

Введение

Виды компьютерной графики

Растровая (пиксельная) графика

Векторная графика

Фрактальная графика

Цветовые модели

Цветовая модель RGB

Цветовая модель CMYK

Цветовая модель HSB

1.     Введение

Компьютерная графика – использование вычислительной техники для создания графических изображений, их отображения

различными средствами и манипулирования ими.

Как следует из определения – компьютерным (цифровым) может быть

названо изображение, созданное с помощью компьютерной программы.

Первоначально программисты научились получать рисунки в режиме символьной печати. На бумажных листах с помощью символов (звёздочек,

точек, крестиков, букв и др.) получались рисунки, напоминающие мозаику.

Так печатались графики функций, изображения течений жидкостей и газов,

изображения электрических и магнитных полей т.д. С помощью символьной

печати программисты умудрялись получать даже художественные

изображения. В редком компьютерном центре стены не украшались

распечатками с портретами Эйнштейна, репродукциями Джоконды и другой

«машинной живописью».

Затем появились специальные устройства для графического вывода на

бумагу – графопостроители (плоттеры). С помощью такого устройства на

лист бумаги чернильным пером наносятся графические изображения:

графики, диаграммы, технические чертежи и прочее.

Но настоящая революция в компьютерной графике произошла с появлением

графических дисплеев. На экране графического дисплея стало возможным

получать рисунки, чертежи в таком же виде, как на бумаге с помощью

карандашей, красок, чертёжных инструментов.

Связь традиционной и компьютерной графики, с одной стороны, определяет применение множительной техники. С другой стороны, можно найти еще одно объяснение возникновению термина «графика» применительно к работе художника-компьютерщика. Слово графика означает изображение линиями, штрихами, точками. А все графические компьютерные программы принципиально разделяются на два типа: векторные (изображение строится линиями) и растровые (изображение пятном из точек), то есть, каким бы сложным ни казалось изображение, созданное в компьютере, по своей сути, любое из них относится к графике.

Изменилась именно техника, и с появлением компьютера произошла

настоящая революция в производстве изобразительной продукции.

2. Виды компьютерной графики

Несмотря на то, что для работы с компьютерной графикой существует

множество классов программного обеспечения, различают всего три вида

компьютерной графики. Это растровая графика, векторная графика и

фрактальная графика. Они отличаются принципами формирования

изображения при отображении на экране монитора или при печати на бумаге.

Правомерна и другая классификация.

Двухмерная графика – изображение, имеющее два измерения, то есть

лежащее на плоскости. Основа компьютерной графики, в том числе и

трехмерной.

Трехмерная (3D) графика – построение на компьютере, с помощью

специальных программ, пространственной модели, состоящей из простых и

сложных геометрических форм, присвоение этой модели фактуры, цвета,

степени прозрачности и матовости, придание ей и условной камере движения

в виртуальном пространстве, расстановка в этом пространстве источников

света и, наконец, просчет выстроенной сцены. Применяется при создании

компьютерных игр, рекламы и т.д.

2.1. Растровая (пиксельная) графика

Растровую графику применяют при разработке электронных и

полиграфических изданий. Иллюстрации, выполненные средствами

растровой графики, редко создают вручную с помощью компьютерных

программ. Чаще используют отсканированные иллюстрации,

подготовленные художником на бумаге, или фотографии. В последнее время

для ввода растровых изображений в компьютер нашли широкое применение

цифровые фото- и видеокамеры. Соответственно, большинство растровых

графических редакторов ориентированы не столько на создание

изображений, сколько на их обработку.

Растр – прямоугольная сетка точек, формирующих изображение

на экране компьютера.

Каждая точка растра характеризуется двумя параметрами: своим положением на экране и своим цветом, если монитор цветной, или степенью яркости, если монитор черно-белый.

Растровая графика представляет изображения в виде массива цифр. Поэтому при большом увеличении все изображения выглядят как мозаика (сетка), состоящая из мельчайших ячеек (рис. 1).

Рис. 1. Простые пиксельные изображения

Сама сетка получила название растровой карты (bitmap), а элементы, ее

формирующие, называются пикселями.

Пиксель (pixel) – мельчайший элемент изображения,

воспроизводимый компьютером.

Слово пиксель произошло от сокращения picture element (элемент

изображения) и замены буквы c на x.

Отличительными особенностями пикселя являются его однородность (все пиксели по размеру одинаковы) и неделимость (внутри пикселя не может быть никаких более мелких элементов).

Если пиксели достаточно малы, глаз воспринимает «пиксельную мозаику» как одно целое изображение (рис. 2, а).

При масштабировании растровых изображений возникают искажения –

ступеньки (aliasing) (рис. 2, б).

Рис. 2: Растровое изображение: a – в натуральном масштабе;

б – в увеличенном масштабе; в – в увеличенном масштабе с применением

anti-aliasing

Основные редакторы растровой графики

 

·        Редактор GIMP

·        Редактор Paint

·        Редактор Adobe Photoshop

·        Редактор Paint Shop Pro

·        Редактор PhotoImpact

·        Редактор Corel PHOTO-PAINT

·        Редактор Macromedia Fireworks

2.2. Векторная графика

Программные средства для работы с векторной графикой предназначены, в первую очередь, для создания иллюстраций и в меньшей степени для их обработки.

Принципы векторной графики основаны на отличном от пиксельной графики математическом аппарате и имеют целью построение линейных контуров, составленных из элементарных кривых, описываемых математическими уравнениями.

Векторная графика – вид компьютерной графики, в котором

изображение представляется в виде совокупности отдельных

объектов, описанных математически.

Как в растровой графике основным элементом изображения является точка,так в векторной графике основным элементом изображения является линия(при этом не важно, прямая это линия или кривая).

Разумеется, в растровой графике тоже существуют линии, но там они

рассматриваются как комбинации точек. Для каждой точки линии в

растровой графике отводится одна или несколько ячеек памяти (чем больше

цветов могут иметь точки, тем больше ячеек им выделяется).

Соответственно, чем длиннее растровая линия, тем больше памяти она

занимает. В векторной графике объем памяти, занимаемый линией, не

зависит от размеров линии, поскольку линия представляется в виде формулы,

а точнее говоря, в виде нескольких параметров. Что бы мы ни делали с этой

линией, меняются только ее параметры, хранящиеся в ячейках памяти.

Количество же ячеек остается неизменным.

Линия — это элементарный объект векторной графики. Все, что есть в

векторной иллюстрации, состоит из линий. Простейшие объекты

объединяются в более сложные. Например, объект четырехугольник можно

рассматривать как четыре связанные линии.

При редактировании элементов векторной графики изменяются параметры прямых и изогнутых линий, описывающих форму этих элементов. Можно переносить элементы, менять их размер, форму и цвет, но это не отразится на качестве их визуального представления. Векторная графика не зависит от разрешения, т.е. может быть показана в разнообразных выходных

устройствах с различным разрешением без потери качества.

Векторный формат более компактный, но он совершенно не пригоден для хранения фотографических изображений. В этом формате задавать их

математически было бы очень громоздко. А вот рисунки и чертежи гораздо

удобнее и практичнее делать именно в векторном виде.

Основными достоинствами векторной графики являются:

·        изменение масштаба без потери качества и практически без увеличения

размеров исходного файла;

·        огромная точность (до сотой доли микрона);

·        небольшой размер файла по сравнению с растровыми изображениями;

·        высокое качество печати;

·        отсутствие проблем с экспортом векторного изображения в растровое;

·        возможность редактирования каждого элемента изображения в

отдельности.

Основные недостатки:

·        сложность экспорта из растрового в векторный формат;

·        невозможность применения обширной библиотеки эффектов,

используемых при работе с растровыми изображениями.

Основные редакторы векторной графики

·        Редактор XFig

·        Редактор Adobe Illustrator

·        Редактор CorelDRAW

·        Редактор Macromedia FreeHand

2.3. Фрактальная графика

Понятия фрактал и фрактальная геометрия, появившиеся в конце 70-х, с середины 80-х гг. прочно вошли в обиход математиков и программистов.

Слово фрактал образовано от латинского fractus и в переводе означает

состоящий из фрагментов. Оно было предложено Бенуа Мандельбротом в

1975 г. для обозначения нерегулярных, но самоподобных структур, которыми

он занимался.

Самыми известными фрактальными объектами являются деревья: от каждой ветки ответвляются меньшие, похожие на нее, от тех — еще меньшие и так далее. По отдельной ветке математическими методами можно проследить свойства всего дерева. Фрактальными свойствами обладают многие природные объекты: снежинка при увеличении оказывается фракталом; по фрактальным алгоритмам растут кристаллы и растения. Если посмотреть на береговую линию моря на картах все более крупного масштаба, то становятся видны все новые изгибы и изломы, похожие на более крупные.

Роль фракталов в машинной графике сегодня достаточно велика. Они

приходят на помощь, например, когда требуется, с помощью нескольких

коэффициентов, задать линии и поверхности очень сложной формы. С точки

зрения машинной графики, фрактальная геометрия незаменима при

генерации искусственных облаков, гор, поверхности моря. Фактически

найден способ легкого представления сложных неевклидовых объектов,

образы которых весьма похожи на природные.

Одним из основных свойств фракталов является самоподобие. В самом

простом случае небольшая часть фрактала содержит информацию о всем

фрактале.

Фрактал – структура, состоящая из частей, которые в каком-то

смысле подобны целому.

Такое определение фракталу дал Мандельброт.

Классификация фракталов

Геометрические фракталы

Фракталы этого класса самые наглядные. В двухмерном случае их получают с помощью некоторой ломаной (или поверхности в трехмерном случае), называемой генератором. За один шаг алгоритма каждый из отрезков, составляющих ломаную, заменяется на ломаную-генератор, в

соответствующем масштабе. В результате бесконечного повторения этой

процедуры, получается геометрический фрактал.

Примером такого фрактального объекта является триадная кривая Кох (рис. 3).

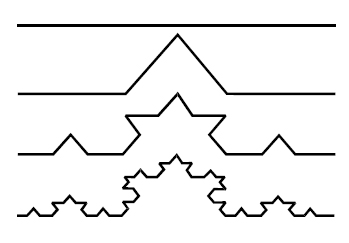
Рис. 3. Построение триадной кривой Кох.

Построение кривой начинается с отрезка единичной длины – это нулевое поколение кривой Кох. Далее каждое звено (в нулевом поколении один отрезок) заменяется на образующий элемент. В результате такой замены получается следующее поколение кривой Кох. В первом поколении – это кривая из четырех прямолинейных звеньев, каждое длиной по 1/3. Для

получения третьего поколения проделываются те же действия - каждое звено

заменяется на уменьшенный образующий элемент. Итак, для получения

каждого последующего поколения, все звенья предыдущего поколения

необходимо заменить уменьшенным образующим элементом. Кривая n-го

поколения при любом конечном n называется предфракталом.

На рис. 3 представлены три поколения кривой. При n стремящемся к

бесконечности кривая Кох становится фрактальным объектом.

В машинной графике использование геометрических фракталов необходимо при получении изображений деревьев, кустов, береговой линии. Двумерные геометрические фракталы используются для создания объемных текстур.

 

Алгебраические фракталы

 

Это самая крупная группа фракталов. Свое название они получили за то, что их строят на основе алгебраических формул, иногда весьма простых.

Методов получения алгебраических фракталов несколько. Один из методов представляет собой многократный (итерационный) расчет функции

Zn+1= f (zn) , где Z – комплексное число, а f – некая функция. Расчет

данной функции продолжается до выполнения определенного условия. И

когда это условие выполнится - на экран выводится точка. При этом значение

функции для разных точек комплексной плоскости может иметь разное

поведение:

·        с течением времени стремится к бесконечности;

·        стремится к 0;

·        принимает несколько фиксированных значений и не выходит за их

пределы;

·        поведение хаотично, без каких-либо тенденций.

Примером этого вида фракталов является множество Мандельброта(рис.4).

Рис. 4. Множество Мандельброта

Стохастические фракталы

Еще одним известным классом фракталов являются стохастические

фракталы, которые получаются в том случае, если в итерационном процессе

случайным образом менять какие-либо его параметры. При этом получаются

объекты очень похожие на природные - несимметричные деревья,

изрезанные береговые линии и т.д. (рис. 5). Двумерные стохастические

фракталы используются при моделировании рельефа местности и

поверхности моря.

Рис. 5. Стохастические фракталы

Способность фрактальной графики моделировать образы живой природы вычислительным путем часто используют для автоматической генерации необычных иллюстраций.

3.     Цветовые модели

С физической точки зрения цвет – это набор определённых длин волн,

отражённых от предмета или пропущенных сквозь прозрачный предмет.

Однако сейчас нас интересует вопрос не о том, что такое цвет, какова его

физическая природа, а то, как вообще на практике можно получить тот или

иной цвет.

Цвета в природе редко являются простыми. Большинство цветов получаются смешением каких-либо других. Например, сочетание красного и синего даёт пурпурный цвет, синего и зелёного – голубой. Таким образом, путём смешения из небольшого количества простых цветов, можно получить

множество (и при чём довольно большое) сложных (составных). Поэтому для

описания цвета вводится понятие цветовой модели.

Цветовая модель – способ представления большого количества цветов посредством разложения их на простые составляющие. Существует большое количество моделей. Рассмотрим только три основных.

3.1.         Цветовая модель RGB

Множество цветов видны оттого, что объекты, их излучающие, светятся. К таким цветам можно отнести, например, цвета на экранах телевизора, монитора, кинопроектора. Цветов огромное количество, но из них выделено только три, которые считаются основными (первичными): это – красный, зеленый, синий.

При смешении двух основных цветов результирующий цвет осветляется: из смешения красного и зеленого получается желтый, из смешениязеленого и синего получается голубой, синий и красный дают пурпурный. Если смешиваются все три цвета, в результате образуется белый. Такая модель цвета является аддитивной.

Модель, в основе которой лежат указанные цвета, носит название цветовой модели RGB – по первым буквам английских слов Red (Красный), Green (Зеленый), Blue (Синий).

Поскольку в модели используются три независимых значения, ее можнопредставить в виде трехмерной системы координат (рис. 6.).

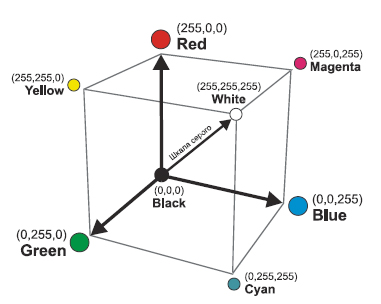
Рис. 6. Цветовая модель RGB.

Каждая координата отражает вклад соответствующей составляющей в

конкретный цвет в диапазоне от нуля до максимального значения. В

результате получается некий куб, внутри которого и находятся все цвета,

образуя цветовое пространство модели RGB.

Объем такого куба (количество цифровых цветов) легко посчитать:

поскольку на каждой оси можно отложить 256 значений, то 256 в кубе (или 2

в двадцать четвертой степени) дает число 16 777 216.

Важно отметить особые точки и линии этой модели.

Начало координат. В этой точке все составляющие равны нулю, излучение отсутствует, а это равносильно темноте, следовательно, начало координат — это точка черного цвета.

Точка, ближайшая к зрителю. В этой точке все составляющие имеют максимальное значение, что означает белый цвет.

Диагональ куба. На линии, соединяющей начало координат и точку,

ближайшую к зрителю, располагаются серые оттенки: от черного до белого.

Это происходит потому, что все три составляющих одинаковы и располагаются в диапазоне от нуля до максимального значения. Этот

диапазон иначе называют серой шкалой (Grayscale). В компьютерных

технологиях сейчас чаще всего используются 256 градаций (оттенков)

серого. Хотя некоторые сканеры имеют возможность кодировать 1024

оттенков серого и выше.

Три вершины куба обозначают чистые исходные цвета, остальные три

отражают двойные смешения исходных цветов.

Модель RGB является теоретической основой процессов сканирования и визуализации изображений на экране монитора.

3.2. Цветовая модель CMYK

Модель описывает отражаемые цвета. К отражаемым относятся цвета,

которые сами не излучают, а используют белый свет, вычитая из него

определенные цвета. Такие цвета называются субтрактивными (вычитательными), поскольку они остаются после вычитания основных аддитивных. Существует три основных субтрактивных цвета: голубой, пурпурный, желтый (рис. 7).

Эти цвета составляют так называемую полиграфическую триаду. При печати красками этих цветов поглощаются красная, зеленая и синяя- составляющие белого цвета таким образом, что большая часть видимого цветового спектра может быть репродуцирована на бумаге.

При смешении двух субтрактивных составляющих результирующий цвет затемняется, а при смешении всех трех должен получиться черный цвет. При полном отсутствии краски остается белый цвет (белая бумага).

В итоге получается, что нулевые значения составляющих дают белый цвет, максимальные значения должны давать черный, их равные значения –

оттенки серого, кроме того, имеются чистые субтрактивные цвета и их

двойные сочетания.

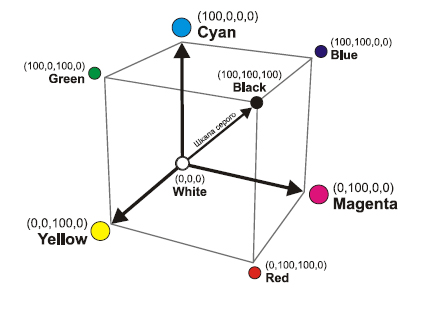
Рис. 7. Цветовая модель CMYK

Основная проблема заключается в том, что данная модель призвана

описывать реальные полиграфические краски, которые далеко не так

идеальны, как цветной луч. Они имеют примеси, поэтому не могут

полностью перекрыть весь цветовой диапазон, а это приводит, в частности, к

тому, что смешение трех основных красок, которое должно давать черный

цвет, дает какой-то неопределенный (грязный) темный цвет, и это скорее

темно-коричневый, чем глубокий черный цвет.

Для компенсации этого недостатка в число основных полиграфических

красок была внесена черная краска. Именно она добавила последнюю букву в

название модели CMYK, хотя и не совсем обычно: С – это Cyan (Голубой), М

– это Magenta (Пурпурный), Y – Yellow (Желтый), К – это blасK (Черный),

т.е. от слова взята не первая, а последняя буква.

Существует еще один вариант расшифровки CMYK – Cyan, Magenta, Yellow, Key color. Причем key color (ключевой цвет) может быть любым.

Таким образом, модели RGB и CMYK, хотя и связаны друг с другом, однако их взаимные переходы друг в друга (конвертирование) не происходят без потерь, поскольку цветовой охват у них разный. И речь идет лишь о том,

чтобы уменьшить потери до приемлемого уровня. Это вызывает

необходимость очень сложных калибровок всех аппаратных частей,

составляющих работу с цветом: сканера (он осуществляет ввод

изображения), монитора (по нему судят о цвете и корректируют его

параметры), выводного устройства (оно создает оригиналы для печати),

печатного станка (выполняющего конечную стадию).

Для устранения аппаратной зависимости был разработан ряд так называемых перцепционных (интуитивных) цветовых моделей. В их основу заложено раздельное определение яркости и цветности.

3.3.         Цветовая модель HSB

Если модель RGB наиболее удобна для компьютера, а модель CMYK – для типографий, то модель HSB наиболее удобна для человека.

На цветовом круге (рис. 6.3) основные цвета моделей RGB и CMYК находятся в такой зависимости: каждый цвет расположен напротив дополняющего его (комплементарного) цвета, при этом он находится между цветами, с помощью которых он получен. Например, сложение зеленого и красного цветов дает желтый.

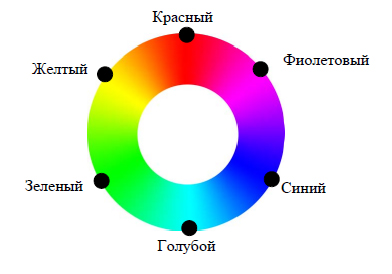
Рис. 8. Цветовой круг

Чтобы усилить какой-либо цвет, нужно ослабить дополняющий его цвет(расположенный напротив него на цветовом круге). Например, чтобы

изменить общее цветовое решение в сторону голубых тонов, следует снизить

в нем содержание красного цвета.

По краю этого цветового круга располагаются так называемые спектральные цвета или цветовые тона (Hue), которые определяются длинойсветовой волны, отраженной от непрозрачного объекта или прошедшей через прозрачный объект. Цветовой тон характеризуется положением на цветовом круге и определяется величиной угла в диапазоне от 0 до 360 градусов. Эти цвета обладают максимальной насыщенностью, т. е. синий цвет еще синее быть уже не может.

Следующим параметром является насыщенность цвета (Saturation) — это параметр цвета, определяющий его чистоту.

Уменьшение насыщенности цвета означает его разбеливание. Цвет с

уменьшением насыщенности становится пастельным, блеклым, размытым.

На модели все одинаково насыщенные цвета располагаются на

концентрических окружностях, т.е. можно говорить об одинаковой

насыщенности, например, зеленого и пурпурного цветов, и чем ближе к

центру круга, тем все более разбеленные цвета получаются. В самом центре

любой цвет максимально разбеливается и становится белым цветом.

Поэтому работу с параметром насыщенности можно характеризовать как добавление в спектральный цвет определенного процента белой краски.

Еще одним параметром является яркость цвета (Brightness) – это параметр цвета, определяющий освещенность или затемненность цвета. Уменьшение яркости цвета означает его зачернение.

Поэтому работу с параметром яркости можно характеризовать как

добавление в спектральный цвет определенного процента черной краски.

В общем случае, любой цвет получается из спектрального цвета добавлением определенного процента белой и черной красок, т. е. фактически серой краски.

Эта модель уже гораздо блиближе к традиционному пониманию работы с цветом. Можно определять сначала цветовой тон (Hue), а затем

насыщенность (Saturation) и яркость (Brightness). Такая модель получила

название по первым буквам приведенных выше английских слов — HSB

(рис. 9).

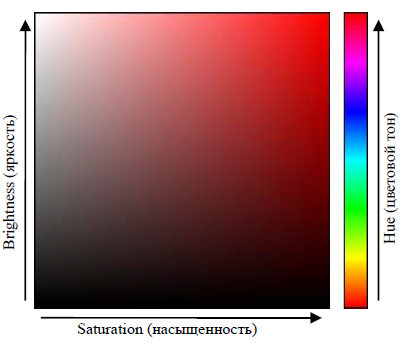
Рис. 9. Цветовая модель HSB

Модель HSB неплохо согласуется с восприятием человека: цветовой тон является эквивалентом длины волны света, насыщенность — интенсивности волны, а яркость – количества света.

Недостатком этой модели является необходимость преобразовывать ее в модель RGB для отображения на экране монитора или в модель CMYK дляполучения полиграфического оттиска.

Заключение

В данной работе рассмотрены только вопросы, относящиеся к

теоретической части дисциплины «Компьютерная графика». Работа в

прикладных пакетах изучается в процессе лабораторных и практических

занятий.

Библиографический список

1. Бэйн С. Эффективная работа: CorelDRAW 10. – СПб.: Питер, 2002.

-784 с.

2. Ганзбург А. Периферийные устройства. – СПб.: Питер, 2001. – 448 с.

3. Гук М. Аппаратные средства IBM PC Энциклопедия.– СПб.: Питер, 2000. – 816 с.

4. Казанцев А. В. Основы компьютерной графики: В2ч. Ч 1. Математический аппарат

компьютерной графики (электронная версия). – Казань, 2001. – 62 с.

5. Ким Ли. 3D Studio MAX 4/5. Для дизайнера. Искусство трехмерной анимации. – Киев:

ООО «ТИД «ДС», 2002. – 848 с.

6. Панкратова Т. FreeHand 9: Учебный курс.– СПб.: Питер, 2001. – 448 с.

7. Петров М. Н., Молочков В. П. Компьютерная графика: Учебник для вузов. – СПб.:

Питер, 2003. – 736 с.

8. Пономаренко С. И. Adobe Illustrator 10. – СПб.: БХВ-Петербург, 2003. – 688 с.

9. Пономаренко С. И. Пиксел и вектор. Принципы цифровой графики. – СПб.: БХВ-

Петербург, 2002. – 496 с.

10. Тайц А. М., Тайц А. А. Самоучитель Adobe Photoshop 7. – СПб.: БХВ-Петербург,

2002. – 688 с.

11. Шушан Р., Райт Д., Льюис Л. Дизайн и компьютер. – М.: Издательский отдел «Русская

Редакция» ТОО «Channel Trading Ltd.», 1997. – 544 с.

12. Яцюк О. Г., Романычева Э. Т. Компьютерные технологи

Терминологический словарь

Пиксель (pixel) – мельчайший элемент изображения, воспроизводимый компьютером.