|
Форма N Н-6.01 _____________Вінницький
національний технічний університет ____________ |
КУРСОВА РОБОТА
|
з дисципліни “Математичні методи
наукових досліджень” |
|
|||||||||||||
Міністерство освіти і науки України
Вінницький національний технічний університет
Інститут інформаційних технологій та комп’ютерної інженерії
ЗАТВЕРДЖУЮ
Зав. каф. КН, д.т.н., проф.
_____________ С.І.Перевозніков
«__» _____________ 2014р.
ІНДИВІДУАЛЬНЕ ЗАДАННЯ
на курсову роботу з дисципліни «Математичні методи наукових досліджень» студенту Левченку Юрію Вікторовичу_____
групи ____1КН-14 м_____
1. Тема курсової роботи «Вдосконалення математичної моделі нейронного елемента», затверджена на засіданні кафедри комп’ютерних наук, протокол № від 2014 р.
2. Термін здачі студентом зазначеного проекту: “ ” 2014 р.
3. Вихідні дані по роботі: математична модель, що описує вдосконалену математичну модель нейронного елемента (LIF-нейрон), параметри нейронного елемента визначені в програмному середовищі, мова програмування та середовище розробки повинні забезпечити маніпулювання та обробку даних.
4. Зміст пояснювальної записки: вступ; теоретичні відомості; вдосконалення математичної моделі нейронного елемента; планування процесу розробки програмного забезпечення; розробка програмного забезпечення; висновки.
5. Дата видачі завдання “ ” 2014 р.
Завдання видав Поремський Ю.В. _________
(ПІП керівника курсової роботи) (підпис)
Завдання прийняв до виконання Левченко Ю.В. _________
(ПІП студента) (підпис)
АНОТАЦІЯ
В курсовій роботі проведено дослідження та запропоновано вдосконалену модель нейронного елемента, а також проведено перевірку на відповідність пропонованої схеми моделі нейрону до математичної моделі.
Для створення моделі нейронного елементу було використано середовище моделювання CSIM, де й проводилося дослідження та програмування відповідної моделі нейронного елементу.
Результат курсової роботи може використовуватися для апаратної побудови великих нейронних мереж.
АННОТАЦИЯ
В курсовой работе проведено исследование и предложена усовершенствованная модель нейронного элемента, а также проведена проверка на соответствие предлагаемой схемы модели нейрона к математической модели.
Для создания модели нейронного элемента было использовано среда моделирования CSIM, где и проводилось исследование и программирование соответствующей модели нейронного элемента.
Результат курсовой работы может использоваться для аппаратной построения больших нейронных сетей.
ЗМІСТ
|
ВСТУП…………………………………………………………………….. |
0 |
|
1ТЕОРЕТИЧНІ ВІДОМОСТІ…………………………………………..... |
0 |
|
1.1Актуальність значення моделей нейронного елементу…………… |
0 |
|
1.2 Аналіз існуючих моделей нейронних елементів………………….. |
0 |
|
1.3Висновки . Постановка задачі дослідження........................................ |
0 |
|
2 ВДОСКОНАЛЕННЯ МАТЕМАТИЧНОЇ МОДЕЛІ НЕЙРОННОГО ЕЛЕМЕНТА ………………………………………...….. |
0 |
|
2.1 Аналіз існуючої математичної моделі ……………………………… |
0 |
|
2.2 Вдосконалення математичної моделі нейронного елемента…….. |
|
|
2.3 Висновки…………………………………………………………….... |
0 |
|
3 ПЛАНУВАННЯ ПРОЦЕСУ РОЗРОБКИ ПРОГРАМНОГО ЗАБЕЗПЕЧЕННЯ ………………………………………………………… |
0 |
|
3.1 Попередній аналіз трудомісткості процесу розробки ПЗ……….. |
0 |
|
3.2 Розробка детального плану розробки ПЗ…………………………. |
0 |
|
3.3 Планування процесу розробки програмного забезпечення моделювання імпульсного нейронного елемента при ідеальних умовах……………………………………………………………………... |
0 |
|
3.4 Планування процесу розробки програмного забезпечення моделювання імпульсного нейронного елемента з використанням Scrum………………………………………………………………………. |
0 |
|
3.4 Висновки……………………………………………………………..... |
0 |
|
4 РОЗРОБКА ПРОГРАМНОГО ЗАБЕЗПЕЧЕННЯ |
0 |
|
4.1 Огляд програмного середовища CSIM…………………………….. |
0 |
|
4.2 Розробка моделі нейронного елемента в середовищі CSIM…….. |
0 |
|
ВИСНОВКИ……………………………………………………………..... |
0 |
|
ПЕРЕЛІК ПОСИЛАНЬ…………………………………………………… |
0 |
|
Додаток А Технічне завдання……………………………………………. |
0 |
|
Додаток Б Інструкція користувача………………………………………. |
0 |
|
Додаток В Мембранний потенціал та вихідні імпульси математичної моделі нейрону…………………………………………………………… |
0 |
|
Додаток Г Лістинг програми…………………………………………….. |
0 |
ВСТУП
Інтерес до штучних нейронних мереж швидко виріс за останні декілька років. Фахівці з багатьох областей, як технічне конструювання, філософія, фізіологія і психологія, заінтриговані можливостями, що надає ця технологія, і шукають застосування їм всередині своїх дисциплін.
Тому існує задача створення моделі нейрона, в якій введення нових вузлів та зв’язків надасть змогу працювати з оптичними сигналами. Завдяки наявності оптичних входів та виходів модель буде легко використовуватися при побудові імпульсних нейронних мереж з великою кількістю елементів та зв’язків між ними. Це розширює функціональні можливості моделі, оскільки організація великої кількості оптичних зв’язків реалізується набагато простіше, ніж електричних зв’язків за допомогою оптичних та голографічних засобів.
Тому виникає необхідність проведення програмування нейронних елементів та проведення аналізу моделей для забезпечення відповідності створених моделей до своїх біологічних прототипів.
Мета роботи – спрощення реалізації імпульсного нейрону та доведення її адекватності математичній моделі.
Предмет дослідження – засоби програмного моделювання імпульсних нейронів.
Об"єкт дослідження – процес комп’ютерного програмування імпульсних нейронів.
Основні задачі дослідження:
- аналіз існуючих моделей нейронних елементів;
- вдосконалення математичної моделі;
- розробка моделі нейронного елемента в середовищі CSIM;
- аналіз результатів програмування схеми нейрону.
1 ТЕОРЕТИЧНІ ВІДОМОСТІ
1.1 Актуальність значення моделей нейронного елементу
При сучасному рівні розвитку техніки, коли навіть побутова техніка оснащується мікропроцесорними пристроями, виникла потреба в інтелектуальних адаптивних системах управління, здатних пристосовуватися до дуже широкого діапазону зовнішніх умов. Більше того, виникла потреба в універсальній технології створення таких систем. Науковий досвід людства свідчить про те, що в природі можна знайти безліч цінних ідей для науки і техніки. Людський мозок є найбільш дивним і загадковим створенням природи. Здатність живих організмів, наділених вищою нервовою системою, пристосовуватися до навколишнього середовища може служити закликом до наслідування природі або імітації при створенні технічних систем.
У основу штучних нейронних мереж покладено такі риси живих нейронних мереж, які дозволяють добре справлятися з нерегулярними завданнями: простий обробний елемент – нейрон; дуже велику кількість нейронів бере участь у обробці інформації; один нейрон пов"язаний з великою кількістю інших нейронів; паралельність обробки інформації [1].
Прототипом до створення нейрона послужив біологічний нейрон мозку. Біологічний нейрон має тіло, сукупність відростків - дендритів, з яких нейрону надходять вхідні сигнали, і відросток - аксон, передавальний вихідний сигнал нейрона іншим клітинам. Місце сполучення дендрита і аксона називається синапсом.
Поведінка штучної нейронної мережі залежить як від значення вагових параметрів, і від функції порушення нейронів. Відомі три основні види функції порушення: порогова, лінійна і сигмоідальна. Нейронна мережа є сукупністю значної частини порівняно простих елементів - нейронів, топологія сполук яких залежить від типу мережі. Щоб створити нейронну мережу на вирішення певною конкретною завдання, повинно провести вибір, як слід з"єднувати нейрони один з одним, і відповідно підібрати значення вагових параметрів цих зв"язків. Чи може впливати один елемент на інший, залежить від встановлених сполук.
Нині стає зрозуміло, подальший розвиток різних аспектів проблем автоматичного управління складними системами вимагає об"єднати зусилля технічних і біології. Спільними завданнями тих наук є: управління динамічними об"єктами і базами даних, а як і оптимізація управління. Для управління складними системами і об"єктами застосовуються нейронні мережі.
Сучасний підхід до створення нейросистем еволюціонує у бік віддалення функціонування від біологічних аналогів. Для моделювання сучасних нейросистем використовується сильно спрощена модель базового елемента (нейрона).
Найперспективнішим для технічної реалізації представляється моделювання лише на рівні опису інформаційних перетворень імпульсних потоків в нейроні, не спускаючись до рівня фізико-хімічних процесів, але й абстрагуючись від розуміння нейрона як об"єкта, здійснює нелінійні аналогові перетворення потоку імпульсів.
Нейронні мережі являють собою нову і дуже перспективну обчислювальну технологію, що дає нові підходи до дослідження динамічних задач у фінансовій області. Спочатку нейронні мережі відкрили нові можливості в області розпізнавання образів, потім до цього додалися статистичні і засновані на методах штучного інтелекту засоби підтримки прийняття рішень та вирішення завдань у сфері фінансів.
Здатність до моделювання нелінійних процесів, роботі з зашумленими даними і адаптивність дають можливості застосовувати нейронні мережі для вирішення широкого класу завдань. В останні кілька років на основі нейронні мереж було розроблено багато програмних систем для застосування в таких питаннях, як операції на товарному ринку, оцінка ймовірності банкрутства банку, оцінка кредитоспроможності, контроль за інвестиціями, розміщення позик.
Додатки нейронних мереж охоплюють найрізноманітніші області інтересів: розпізнавання образів, обробка зашумленні даних, доповнення образів, асоціативний пошук, класифікація, оптимізація, прогноз, діагностика, обробка сигналів, абстрагування, управління процесами, сегментація даних, стиснення інформації, складні відображення, моделювання складних процесів , машинне зір, розпізнавання мови.
1.2 Аналіз існуючих моделей нейронних елементів
Відомий пристрій для моделювання нейрона (патент України № 52771, м. кл. G06G 7/60, 2006 р., бюл. №17), який містить керовані резисторні елементи, блоки моделювання синапсів, які складаються з послідовно з"єднаних узгоджуючих підсилювачів, входи яких є входами блоків моделювання синапсів, накопичуючих елементів, елементів затримки, блоки моделювання 10 дендритів, які складаються з суматорів, елементів затримки та інвертора, утворюючих прямий та зворотний ланцюги так, що елементи затримки і суматори по першому неінвертованому входу включені до них послідовно і чергуються між собою, причому зворотний ланцюг починається з суматора, а вихід його останнього елемента затримки з"єднаний через інвертор з входом першого елемента затримки прямого ланцюга, другі неінвертовані входи суматорів прямого ланцюга з"єднані з інвертованими входами суміжних з ними суматорів зворотного ланцюга і є входами блока моделювання дендриту, які з"єднані з виходами відповідної до нього групи блоків моделювання синапсів, вихід кожного елемента затримки прямого ланцюга з"єднаний з другим неінвертованим входом відповідного суматора зворотного ланцюга і є виходом блока моделювання дендриту і дендритним виходом пристрою, а вихід кожного елемента затримки зворотного ланцюга з"єднаний з третім неінвертованим входом [2] відповідного суматора прямого ланцюга, прямий ланцюг закінчується елементом затримки, вихід якого є проксимальним виходом блока моделювання дендриту, формувач вихідних імпульсів, вихід якого є виходом пристрою, пристрій також містить блок синхронізації, входи якого з"єднані з виходом пристрою і його входами, а виходи за кількістю синапсів підключені до керуючих входів резисторних елементів, причому кожний блок моделювання дендриту містить додаткові елементи затримки за кількістю наявних у них елементів затримки без одного та двовхідні суматори, виходи двовхідних суматорів є дендритними виходами, перший вхід кожного суматора під"єднаний між виходом елемента затримки і входом додаткового елемента затримки прямого ланцюга, а другий вхід - між відповідними їм елементами затримки зворотного ланцюга, кількість двовхідних суматорів дорівнює кількості ділянок дендриту між синаптичними контактами.
Найбільшим недоліком даного пристрою є складність його структури.
Інший відомий пристрій для моделювання нейрона (патент України № 22956, м. кл.G06 G 7/60, 1998 р., Бюл. 3), який містить два фотоприймачі, електронний ключ, біспін-прилад, резистор навантаження, модулятор лазерного випромінювання, лазер та голограму, на якій записано зовнішні зв"язки моделі нейрону. Недоліком даного пристрою також є його апаратна складність.
Ще один пристрій для моделювання нейрона (патент України №55921, м.кл. G06G 7/00, 2009 р., бюл. №24), який містись джерело живлення, яке з"єднано з катодом першого фотодіода та з виводами першого та другого резисторів, анод першого фотодіода з"єднано з катодом другого фотодіода, з першим виводом першого конденсатора, другим виводом другого резистора та керуючим електродом тиристора, другий вивід першого резистора з"єднано з першим виводом другого конденсатора та анодом тиристора, катод тиристора з"єднано з електричним виходом пристрою та першими виводами третього резистора та третього конденсатора, другий вивід третього резистора з"єднано з анодом світлодіоду, катод якого разом з другими виводами першого, другого та третього конденсатори з"єднано із загальною шиною [3].
Недоліком даного пристрою є складність схемотехнічної реалізації та низька робоча частота.
Пристрій для моделювання нейрона (патент України №55921, м.кл. G06G 7/00, 2009 р., бюл. №24) зображено на рисунку 1.1.
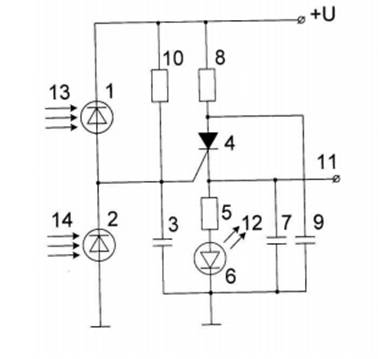
Рисунок 1.1 - Пристрій для моделювання нейрона
(патент України №55921, м.кл. G06G 7/00, 2009 р., бюл. №24)
Пристрій для моделювання нейрона (патент України №70918, м.кл. G06G 7/60, 2006 р., бюл. №12). Пристрій містить конденсатор 1, перший вивід якого з"єднаній з джерелом живлення 6, другий вивід конденсатора 1 з"єднаний із вихідною клемою 2 та з першим виводом С-негатрона 3, а також з анодом першого фотодіода 4, та з катодом фотодіода 5, анод якого підключеним до негативного полюса джерела живлення 7, катод першого фотодіода 4 підключений до джерела живлення, другий вивід С-негатрона 3 з"єднаний з негативним полюсом джерела живлення 7.
Нейронний елемент на С-негатроні, що містить джерело живлення, яке з"єднано з катодом фотодіода, анод якого з"єднано з катодом другого фотодіода, катод тиристора з"єднано з електричним виходом пристрою, анод тиристора з"єднано з джерелом живлення, який відрізняється тим, що введено С-негатрон, перший вивід якого з"єднано вихідною клемою, а також з джерелом живлення через конденсатор, його другий вивід з"єднано з негативним полюсом джерела живлення. Пристрій зображено на рисунку 1.2.
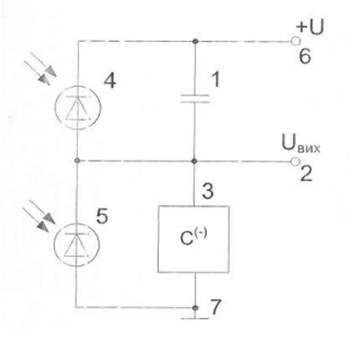
Рисунок 1.2 - Пристрій для моделювання нейрона
(патент України №70918, м.кл. G06G 7/60, 2006 р., бюл. №12)
Процес комп’ютерного моделювання імпульсних нейронів зумовлює постійний розвиток технологій та вдосконалення існуючих пристрій для моделювання нейронів.
Існуючі пристрої для моделювання містять ряд своїх недоліків, такі як апаратна складність, складна схемотехнічна реалізація [4], низька робоча частота та вузькі функціональні можливості.
Досліджені пристрої не орієнтовані на введення можливості нових вузлів та зв’язків, що дасть змогу працювати із оптичними сигналами, що також розширить функціональні можливості моделі.
Наведені вище проблеми вимагають розробки моделі, що зможе легко використовуватися при побудові імпульсних нейронних мереж з великою кількістю елементів та зв’язків між ними.
Це й розширить функціональні можливості моделі, оскільки організація великої кількості оптичних зв"язків реалізується набагато простіше, ніж електричних зв"язків за допомогою оптичних та голографічних засобів.
1.3 Висновки до розділу 1. Постановка задачі дослідження
Дане дослідження передбачає аналіз існуючих моделей імпульсних нейронів; вибір математичної моделі для вдосконалення та безпосередньо вдосконалення математичної моделі нейронного елемента. В розробленому програмному забезпеченні повинна забезпечуватися наявність можливості редагувати процес вибору параметрів для аналізу математичної моделі нейронного елементу. Саме на даному етапі постає процес проектування програмного забезпечення, яке буде реалізовувати усі необхідні функції. Також необхідно усунути усі недоліки, які були у подібних математичних моделях. Також у даному дослідженні здійснюється удосконалення математичної моделі, яка й буде досліджуватися у даному середовищі.
У дослідженні не повинні бути реалізовані методи та технології, які є повільними у виконанні та потребують великої кількості обчислювальних ресурсів.
Дослідження передбачає три основні етапи. Загалом пропонуватиметься вдосконалена математична модель, що дозволить використовувати її для побудови нейронних мереж.
2 ВДОСКОНАЛЕННЯ МАТЕМАТИЧНОЇ МОДЕЛІ
НЕЙРОННОГО ЕЛЕМЕНТА
2.1 Аналіз існуючої математичної моделі
2.1.1 Модель імпульсної відповіді (SRM)
Модель імпульсної відповіді (SRM) є - як і нелінійна модель «Накопичити та вистрілити» (integrate-and-fire) - узагальненням негерметичної моделі «Накопичити та вистрілити». Напрямок узагальнення, однак, дещо відрізняється. В нелінійній моделі «Накопичити та вистрілити» параметри залежать від напруги, в той час як у SRM вони залежать від часу з моменту останнього вихідного імпульсу. Ще одна відмінність між моделлю «Накопичити та вистрілити» і SRM пов"язана з визначенням рівнянь. У той час як моделі «Накопичити та вистрілити» зазвичай визначаються диференційними рівняннями, SRM виражає мембранний потенціал в момент часу t у вигляді інтеграла по минулому моменту часу.
Явна залежність мембранного потенціалу від останнього вихідного імпульсу дозволяє нам моделювати здатність до відбиття у вигляді комбінації трьох компонентів, а саме, (1) зниження реактивності [5] після виходу іспульса; (2) збільшення порогу після вистрілу; і (3) гіперполяризований імпульс після набуття потенціалу. Представлено Модель імпульсної відповіді та проілюстровано її властивості.
2.1.2 Визначення SRM
В рамках моделі
імпульсної відповіді стан нейрона і описується однією змінною
ui. В моделі імпульсної відповіді (SRM) відсутність імпульсів, змінна ui набуває значення відпочинку, urest=0. Кожен вхідний
імпульс буде активувати ui, це займе деякий час, перш ніж значення ui повертається до нуля. Функція описує
часовий шлях відповіді на вхідний імпульс. Якщо так, після підсумовування
ефектів декількох вхідних імпульсів, ui досягає порогу, та виникає вихідний імпульс. Форма потенціалу дії
і після-потенціалу описується функцією 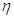 . Припустимо, нейрон i вистрілив останнім
імпульсом у час t. Після випалу зміна ui виглядає (вираз 2.1):
. Припустимо, нейрон i вистрілив останнім
імпульсом у час t. Після випалу зміна ui виглядає (вираз 2.1):
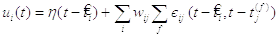
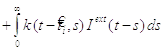 ,
(2.1)
,
(2.1)
де 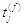 -
імпульси пресинаптичних нейронів j
та
wij
- синаптична ефективність. Останнє значення враховує
зовнішній струм дії. Два сумарних значення пробігають через всі пресинаптичні
нейрони j
та всі моменти вистрілу
-
імпульси пресинаптичних нейронів j
та
wij
- синаптична ефективність. Останнє значення враховує
зовнішній струм дії. Два сумарних значення пробігають через всі пресинаптичні
нейрони j
та всі моменти вистрілу
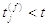 нейрону
j. Підкреслимо, що всі
змінні залежать від
нейрону
j. Підкреслимо, що всі
змінні залежать від 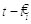 , тобто,
часу з моменту появи останнього вихідного спайка.
, тобто,
часу з моменту появи останнього вихідного спайка.
На відміну від нейрону типу
«Накопичити та вистрілити», поріг
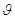 не
встановлений (2.2), але може також залежать від
не
встановлений (2.2), але може також залежать від 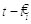 :
:
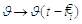 (2.2)
(2.2)
Під
час періоду абсолютної рефрактерності 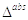 можна, наприклад,
встановити
можна, наприклад,
встановити 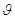 на
велике та позитивне значення для уникнення вистрілів, і нехай значення
повернеться назад до свого рівноважного значення при
на
велике та позитивне значення для уникнення вистрілів, і нехай значення
повернеться назад до свого рівноважного значення при 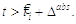 Вистріл відбувається
тоді, коли мембранний потенціал ui
досягає динамічного порогу
Вистріл відбувається
тоді, коли мембранний потенціал ui
досягає динамічного порогу 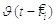 знизу
(2.3):
знизу
(2.3):
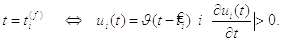 (2.3)
(2.3)
Як
згадувалося раніше 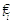 останній
момент вистрілу (2.4):
останній
момент вистрілу (2.4):
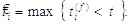 (2.4)
(2.4)
2.1.3 Інтерпретація
Отже,
вищенаведені рівняння визначають математичну модель. Визначимо змінну ui
з мембранним потенціалом [6] нейрона
i. Функції 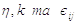 є ядрами
реагування, які описують ефект випромінювання імпульсу та його прийому по
змінній ui.
Ця інтерпретація визначила назву «Модель імпульсної відповіді», SRM (Spike
Response Model). Обговоримо сенс ядер реагування.
є ядрами
реагування, які описують ефект випромінювання імпульсу та його прийому по
змінній ui.
Ця інтерпретація визначила назву «Модель імпульсної відповіді», SRM (Spike
Response Model). Обговоримо сенс ядер реагування.
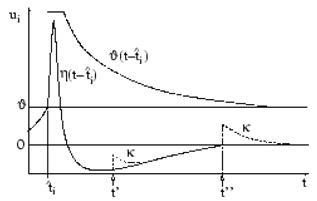
Рисунок 2.1 - Схематична інтерпретація
Моделі
імпульсної відповіді. З рисунка видно, що шлях часу ui(t)
мембранного потенціалу нейрону i
як функції часу t.
Імпульс нейрона i
був ініційований в 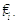 Ядро
Ядро 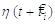 для
для 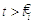 описує форму потенціалу дії (позитивний імпульс) і (негативний)
імпульс після-потенціалу, який
слідує за імпульсом (товста суцільна
лінія). Якщо вхідний імпульс струму застосовується
в момент часу t"", через
довгий час після того, як
відбувся вистріл, це викликає стандартну відповідь, яка описується
функцією
описує форму потенціалу дії (позитивний імпульс) і (негативний)
імпульс після-потенціалу, який
слідує за імпульсом (товста суцільна
лінія). Якщо вхідний імпульс струму застосовується
в момент часу t"", через
довгий час після того, як
відбувся вистріл, це викликає стандартну відповідь, яка описується
функцією 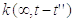 і позначається пунктирною лінією,
починаючи з t""
(стрілка). Вхідний струм імпульсу при t" (стрілка), який надходить відразу після постсинаптичного імпульсу
і позначається пунктирною лінією,
починаючи з t""
(стрілка). Вхідний струм імпульсу при t" (стрілка), який надходить відразу після постсинаптичного імпульсу 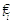 , в зв"язку із здатністю нейрона до відбиття
(рефрактерності), реакція відбувається у значно менший час. Його часовий шлях
описується відповіддю ядра
, в зв"язку із здатністю нейрона до відбиття
(рефрактерності), реакція відбувається у значно менший час. Його часовий шлях
описується відповіддю ядра 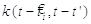 ;
пунктирна лінія після t". Відразу після вистрілу, поріг збільшується
(пунктирна лінія) [7].
;
пунктирна лінія після t". Відразу після вистрілу, поріг збільшується
(пунктирна лінія) [7].
Ядро
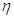 описує
стандартну форму потенціалу дії нейрона i,
в
тому числі негативного перевищення кількості вистрілів, що звичайно
супроводжується імпульсом (після-потенціал). Графічно кажучи, даний вклад
описує
стандартну форму потенціалу дії нейрона i,
в
тому числі негативного перевищення кількості вистрілів, що звичайно
супроводжується імпульсом (після-потенціал). Графічно кажучи, даний вклад 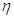 є
“вставленим”
кожен час, коли мембранний потенціал досягає порогу
є
“вставленим”
кожен час, коли мембранний потенціал досягає порогу
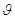 (рисунок
4.5). Так як форма імпульсу завжди однакова, точний шлях
часу потенціалу дії не несе ніякої інформації. Подія повністю характеризується
часом вистрілу
(рисунок
4.5). Так як форма імпульсу завжди однакова, точний шлях
часу потенціалу дії не несе ніякої інформації. Подія повністю характеризується
часом вистрілу 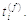 У
спрощеній моделі, форма потенціалу дії може бути знехтуваною, доки ми
відстежуємо моменти вистрілів
У
спрощеній моделі, форма потенціалу дії може бути знехтуваною, доки ми
відстежуємо моменти вистрілів 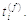 Таким
чином, ядро
Таким
чином, ядро 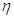 описує «скидання»
мембранного потенціалу до більш низького значення після імпульсу, точно так
само як в моделі «Накопичити та вистрілити». Негерметичні моделі «Leaky
integrate-and-fire», фактично, є окремим випадком SRM.
описує «скидання»
мембранного потенціалу до більш низького значення після імпульсу, точно так
само як в моделі «Накопичити та вистрілити». Негерметичні моделі «Leaky
integrate-and-fire», фактично, є окремим випадком SRM.
Ядро 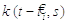 -
це лінійний відгук мембранного потенціалу до вхідного току. Воно описує часовий
шлях відхилення мембранного потенціалу від його значення відпочинку, що
обумовлено коротким імпульсом струму (імпульсна відповідь). Відповідь залежить,
в основному, від часу, що минув з моменту виходу останнього імпульсу
-
це лінійний відгук мембранного потенціалу до вхідного току. Воно описує часовий
шлях відхилення мембранного потенціалу від його значення відпочинку, що
обумовлено коротким імпульсом струму (імпульсна відповідь). Відповідь залежить,
в основному, від часу, що минув з моменту виходу останнього імпульсу 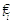 . Відразу після
. Відразу після 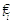 , багато іонних
каналів відкриваються, так що опір мембрани знижується. Реакція напруги на
вхідний імпульс струму розпадається, отже, більш швидко повертається до нуля,
ніж в нейроні, який був неактивним. Зменшена або коротша відповідь є однією з
особливостей нейронної рефрактерності. Ця форма рефрактерного ефекту
з’являється завдяки тому, що ядро
, багато іонних
каналів відкриваються, так що опір мембрани знижується. Реакція напруги на
вхідний імпульс струму розпадається, отже, більш швидко повертається до нуля,
ніж в нейроні, який був неактивним. Зменшена або коротша відповідь є однією з
особливостей нейронної рефрактерності. Ця форма рефрактерного ефекту
з’являється завдяки тому, що ядро 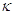 залежить,
за допомогою першого аргументу, від різниці часу
залежить,
за допомогою першого аргументу, від різниці часу 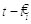 . Проілюструємо дану
ідею на рисунку 4.5. Відповідь на перший вхідний імпульс на t"
коротше і менш виражена, ніж інша у t"",
дія якого експериментально відома.
. Проілюструємо дану
ідею на рисунку 4.5. Відповідь на перший вхідний імпульс на t"
коротше і менш виражена, ніж інша у t"",
дія якого експериментально відома.
Ядро 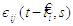 як функції
як функції 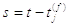 можна
інтерпретувати як часовий шлях постсинаптичного
потенціалу,
викликаного стрільбою пресинаптичного нейрона j
в момент часу
можна
інтерпретувати як часовий шлях постсинаптичного
потенціалу,
викликаного стрільбою пресинаптичного нейрона j
в момент часу 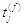 . Залежно
від знака синапсу від j,
до i,
. Залежно
від знака синапсу від j,
до i,
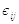 моделі можуть мати
або збудливий, або забороняючий постсинаптичний потенціал. Так само, як для
ядра
моделі можуть мати
або збудливий, або забороняючий постсинаптичний потенціал. Так само, як для
ядра 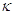 ,
точна форма постсинаптичного потенціалу залежить від часу
,
точна форма постсинаптичного потенціалу залежить від часу 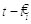 , що пройшов з
моменту останнього імпульсу постсинаптичного нейрону i.
Зокрема, якщо нейрон i
був активним безпосередньо перед прибуттям пресинаптичного потенціалу дії, постсинаптичний
нейрон знаходиться в стані рефрактерності. В цьому випадку, відповідь на
вхідний імпульс менше, ніж у «нештрихованому»
нейроні. Перший аргумент
, що пройшов з
моменту останнього імпульсу постсинаптичного нейрону i.
Зокрема, якщо нейрон i
був активним безпосередньо перед прибуттям пресинаптичного потенціалу дії, постсинаптичний
нейрон знаходиться в стані рефрактерності. В цьому випадку, відповідь на
вхідний імпульс менше, ніж у «нештрихованому»
нейроні. Перший аргумент 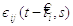 припадає
на залежність від останнього моменту вистрілу постсинаптичного нейрона.
припадає
на залежність від останнього моменту вистрілу постсинаптичного нейрона.
2.1.4 Повний постсинаптичний потенціал
Для спрощення позначень для подальшого використання, зручно ввести загальний (повний) постсинаптичний потенціал (2.5):
 (2.5)
(2.5)
Рівняння (2.6 та 2.7)
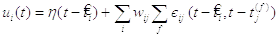 (2.6)
(2.6)
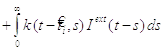 ,
(2.7)
,
(2.7)
можна записати в компактній формі (2.8):
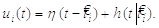 (2.8)
(2.8)
2.1.5 Рефрактерність
Рефрактерність може бути охарактеризована експериментально шляхом спостереження, що відразу ж після першого потенціалу дії неможливо (абсолютна рефрактерність) чи складніше (відносна рефрактерність) викликати другий імпульс.
Абсолютна рефрактерність
може бути включена в SRM, встановивши динамічний поріг протягом часу 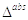 до надзвичайно
високого значення, що не може бути досягнуто.
до надзвичайно
високого значення, що не може бути досягнуто.
Відносну рефрактерність можна
імітувати різними способами. По-перше, після імпульсу мембранного потенціалу, а
отже 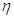 , і проходження
через режим гіперполяризації (після-потенціал), де напруга [8] нижче потенціалу спокою. Під час цієї
фази потрібно більше стимуляції, ніж зазвичай потрібно для приведення значення
мембранного потенціалу вище порога. Це еквівалентно збільшенню порога вистрілу.
, і проходження
через режим гіперполяризації (після-потенціал), де напруга [8] нижче потенціалу спокою. Під час цієї
фази потрібно більше стимуляції, ніж зазвичай потрібно для приведення значення
мембранного потенціалу вище порога. Це еквівалентно збільшенню порога вистрілу.
По-друге, 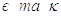 внесенення у
відносну рефрактерність тому, відразу після потенціалу дії, відповідь на вхідні
імпульси коротше і, можливо, із зниженою амплітудою. Таким чином чим більше
вхідних імпульсів потрібно, щоб викликати таку саму деполяризацію мембранного
потенціалу, як в «штрихованому» нейроні. Перший аргумент
внесенення у
відносну рефрактерність тому, відразу після потенціалу дії, відповідь на вхідні
імпульси коротше і, можливо, із зниженою амплітудою. Таким чином чим більше
вхідних імпульсів потрібно, щоб викликати таку саму деполяризацію мембранного
потенціалу, як в «штрихованому» нейроні. Перший аргумент 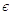 функції (або
функції (або 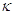 функції) дозволяє
включити цей ефект.
функції) дозволяє
включити цей ефект.
2.1.6 Видалення динамічного порогу
З формальної точки зору,
немає ніякої необхідності інтерпретувати змінну u
в якості мембранного потенціалу. Це, наприклад, часто буває зручно, щоб
перетворити змінну u
таким чином, щоб видалити тимчасову залежність порога.
Насправді,
взагалі загальна Spike Response Model з довільною
залежністю від часу порога 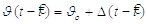 ,
завжди може бути перетворена в модуль імпульсної відповіді із зафіксованим
порогом
,
завжди може бути перетворена в модуль імпульсної відповіді із зафіксованим
порогом 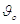 шляхом зміни змінних
2.9:
шляхом зміни змінних
2.9:
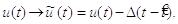 (2.9)
(2.9)
Функція 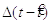 може легко поглинатися
при визначенні ядра.
може легко поглинатися
при визначенні ядра.
2.2 Вдосконалення математичної моделі нейронного елемента
2.2.1 «Integrate-and-fire» модель
Принципова схема є модулем всередині пунктирного кола на правій стороні (рисунок 2.2).
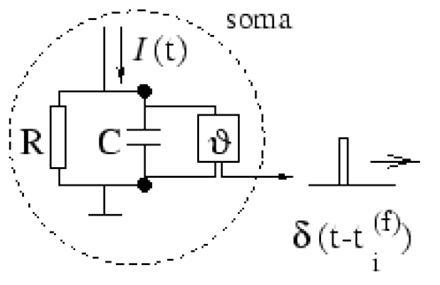
Рисунок 2.2 - принципова схема «Integrate-and-fire» моделі
Струм I(t) заряджає
RC ланцюг. Напруга u(t) через
ємність (точки) порівнюється з пороговим значенням 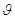 . Якщо
. Якщо 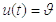 під час
під час 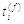 імпульсний
вихід
імпульсний
вихід 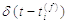 генерується. Ліва
частина: пресинаптичний імпульс
генерується. Ліва
частина: пресинаптичний імпульс 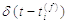 є
низькочастотним фільтром в синапсі та генерує вхідний імпульс струму
є
низькочастотним фільтром в синапсі та генерує вхідний імпульс струму 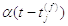 .
.
Принципова схема «Integrate-and-fire» моделі складається з конденсатора С паралельно з резистором R, обумовленим струмом I(t). Рушійний струм можна розділити на дві складові, I(t)=IR+IC. Перший компонент – резистивний струм IR, який проходить через лінійний резистор R. Він може бути розрахований за законом Ома як IR = u/R, де u - напруга через резистор. Другий компонент IC заряджає конденсатор C. З визначення ємності як C =q/u знаходиться ємнісний струм IC = C du/dt. Таким чином (2.10) :
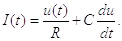 (2.10)
(2.10)
Помножимо вищенаведений
вираз на R і введемо константу часу 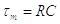 в
«квазіінтегратор». Це дає стандартну форму (2.11):
в
«квазіінтегратор». Це дає стандартну форму (2.11):
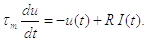 (2.11)
(2.11)
U
в якості мембранного потенціалу і 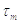 як постійна часова
мембрани
нейрона. В моделях «Накопичити і вистрілити» форма потенціалу дії не описана
явно. Імпульси - це формальні події, що характеризуються «часом вистрілу»
як постійна часова
мембрани
нейрона. В моделях «Накопичити і вистрілити» форма потенціалу дії не описана
явно. Імпульси - це формальні події, що характеризуються «часом вистрілу»
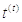 . Час
вистрілу
. Час
вистрілу 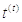 визначається
пороговим критерієм (2.12):
визначається
пороговим критерієм (2.12):
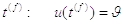 (2.12)
(2.12)
Відразу після 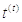 , потенціал
скидається (2.13) на нове значення
, потенціал
скидається (2.13) на нове значення 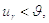
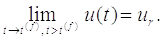 (2.13)
(2.13)
Для 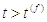 динаміка знову
дається доки наступного перетину порога не відбувається. Мембранний потенціал
ніколи не вище порога; порогова умова зводиться до критерію, тобто
умову на схил
динаміка знову
дається доки наступного перетину порога не відбувається. Мембранний потенціал
ніколи не вище порога; порогова умова зводиться до критерію, тобто
умову на схил 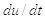 можна
опустити.
можна
опустити.
У загальній умові, нейрон
може також включати в себе абсолютний рефрактерний період. Якщо u
досягає
порогу під час 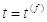 , то
відбувається перетинання динаміки під час
абсолютного часу рефрактерності
, то
відбувається перетинання динаміки під час
абсолютного часу рефрактерності 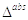 і
перезапускається накопичення в момент часу
і
перезапускається накопичення в момент часу 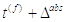 з нового
початкового стану
з нового
початкового стану 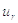 .
.
2.2.2 Відношення до моделі «Integrate and fire»
Основне рівняння негерметичної моделі «Integrate and fire», є лінійним диференціальним рівнянням. Однак, у зв"язку із скиданням мембранного потенціалу після вистрілу, інтеграція не є повністю тривіальною. Насправді, є два різні способи приступити до інтегрування рівняння. Опишемо скидання в якості імпульсу струму. Результат полягає у апроксимативному відображенні в спрощеній моделі SRM0.
Розглянемо короткий
імпульсу струму 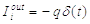 подається
на схему RC. Вона видаляє заряд q з
конденсатора C і знижує потенціал на величину
подається
на схему RC. Вона видаляє заряд q з
конденсатора C і знижує потенціал на величину 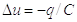 . Таким чином,
скидання мембранного потенціалу
від значення
. Таким чином,
скидання мембранного потенціалу
від значення 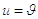 нове
значення
нове
значення 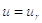 відповідає
вихідному імпульсу струму, що
відповідає
вихідному імпульсу струму, що
видаляє заряд 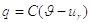 .
Скидання відбувається кожного разу, коли нейрон
вистрілює. Загальне скидання струму (2.14):
.
Скидання відбувається кожного разу, коли нейрон
вистрілює. Загальне скидання струму (2.14):
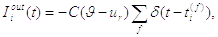 (2.14)
(2.14)
де
сума береться по всьому часу стрільби 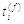 .
.
Додамо вихідний струм по правій стороні (2.15):
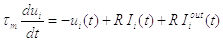 (2.15)
(2.15)
Ось, Ii - це
загальний вхідний струм до нейрона i, породжений
прибуттям пресинаптичного імпульсу і зовнішньою стимуляцією 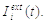 Припустимо, що кожен
пресинаптичний імпульс викликає постсинаптичний струм з плином часу
Припустимо, що кожен
пресинаптичний імпульс викликає постсинаптичний струм з плином часу
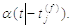 Загальний
вхідний струм, таким чином (2.16):
Загальний
вхідний струм, таким чином (2.16):
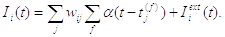 (2.16)
(2.16)
Так
як 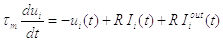 є лінійним
рівнянням, можемо інтегрувати кожний доданок окремо і накладати результат на
кінець. Вихідний імпульс
є лінійним
рівнянням, можемо інтегрувати кожний доданок окремо і накладати результат на
кінець. Вихідний імпульс 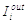 дає
рефрактерне ядро
дає
рефрактерне ядро 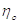 ,
в той час як кожен постсинаптичний імпульс струму
,
в той час як кожен постсинаптичний імпульс струму  генерує
постсинаптичний потенціал
генерує
постсинаптичний потенціал 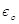 . Зокрема
після
інтеграції (2.17) з початковою умовою
. Зокрема
після
інтеграції (2.17) з початковою умовою 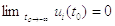
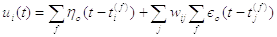 (2.17)
(2.17)
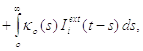
з ядрами (2.18) :
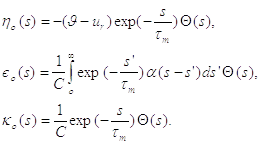 (2.18)
(2.18)
Рефрактерне ядро 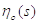 і
постсинаптичний потенціал
і
постсинаптичний потенціал 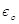 наведено
на рис. 2.3.
наведено
на рис. 2.3.
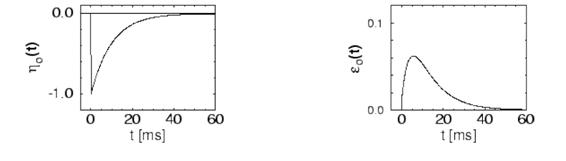
Рисунок 2.3 - Рефрактерне ядро моделі з постійним мембранним
часом.
Постсинаптичний
потенціал 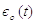 , породжений
експоненціальним імпульсом струму (2.19):
, породжений
експоненціальним імпульсом струму (2.19):
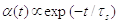 (2.19)
(2.19)
В реалістичних імпульсних
потоках, інтервал між двома імпульсами, як правило, набагато більше, ніж
постійний мембранний час 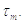 Тому
сума за умовами
Тому
сума за умовами 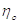 зазвичай
переважає час вистрілу
зазвичай
переважає час вистрілу 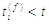 нейрона i. Тому
ми усікаємо суму f
(2.20) і нехтуємо впливом ранніх імпульсів,
нейрона i. Тому
ми усікаємо суму f
(2.20) і нехтуємо впливом ранніх імпульсів,
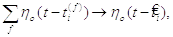 (2.20)
(2.20)
де 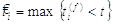 - це остання
стрільба нейрона i. Наближення є
нормальним, якщо середня скорострільність нейрона низька, тобто, якщо інтервали
між двома імпульсами набагато довші, ніж
- це остання
стрільба нейрона i. Наближення є
нормальним, якщо середня скорострільність нейрона низька, тобто, якщо інтервали
між двома імпульсами набагато довші, ніж 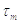 . Грубо кажучи,
нейрон пам"ятає тільки свій останній вистріл.
. Грубо кажучи,
нейрон пам"ятає тільки свій останній вистріл.
Остаточне рівняння має вигляд (2.21):
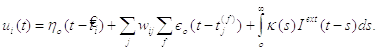 (2.21)
(2.21)
2.3 Висновки до розділу 2.
Отже, отримана LIF-модель нейрону, реалізована так, що мембранний потенціал Vm нейрона подається формулою (2.22):
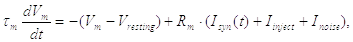 (2.22)
(2.22)
де 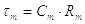 - постійна часу
мембрани, Rm – опір мембрани, Сm – ємність мембрани, Іsyn(t) – струм, що
надходить від синапсів, Іinject – неспецифічний фоновий струм і Іnoise –
Гауссова випадкова величина з нульовим середнім і заданою дисперсією шуму.
- постійна часу
мембрани, Rm – опір мембрани, Сm – ємність мембрани, Іsyn(t) – струм, що
надходить від синапсів, Іinject – неспецифічний фоновий струм і Іnoise –
Гауссова випадкова величина з нульовим середнім і заданою дисперсією шуму.
У момент t=0 Vm встановлюється в Vinit . Якщо потім в результаті дії вхідних сигналів Vm досягає порогову напругу Vthrech , то генерується вихідний імпульс, а Vm скидається до Vreset і утримується таким протягом періоду абсолютної рефрактерності.
З формули видно, до LIF-нейрон має багато параметрів, зміна яких призводить до зміни поведінки самого нейрону. Серед даних параметрів виділяються такі:
- ємність мембрани;
- опір мембрани;
- порогова напруга;
- потенціал спокою;
- потенціал скидання (після генерації імпульсу);
- початковий потенціал (у час t=0);
- період рефрактерності;
- струм шумів;
- постійний вхідний струм (зовнішній);
- тип нейрону (збуджувальний чи гальмівний).
Всі штучні нейромережі конструюються з базового формуючого блоку - штучного нейрону. Існуючі різноманітності і фундаментальні відмінності, є підставою для дослідження та розробки ефективних нейромереж.
3 ПЛАНУВАННЯ ПРОЦЕСУ РОЗРОБКИ
ПРОГРАМНОГО ЗАБЕЗПЕЧЕННЯ
Встановлений порядок дій, що дозволяє визначити основні етапи та терміни виконання проекту називається плануванням. Також планування дозволяє оптимально розподілити ресурси для досягнення поставленої мети. -Головним завданням планування є досягнення всіх поставлених цілей та виконання завдань проекту, одночасно виконуючи зобов"язання щодо наперед визначених обмежень проекту. Типовими обмеженнями є межі та зміст проекту, час, бюджет. Сутність планування полягає в обґрунтуванні цілей і шляхів їх досягнення на основі виявлення комплексу завдань і робіт, а також визначення ефективних методів, способів і ресурсів усіх видів, необхідних для виконання цих завдань та встановлення їх взаємозв"язку.
В даному проекті процес планування розробки програмного забезпечення моделювання нейронного елемента буде здійснюватися за допомогою середовища системи управління проектами MICROSOFT PROJECT. Дане середовище створене для того, щоб допомогти менеджерові проекту в розробці планів, розподілі ресурсів за завданнями, відстежуванні прогресу [9] і аналізі обсягів робіт. Microsoft Project також створює розклади критичного шляху. Розклади можуть бути складені з урахуванням використовуваних ресурсів. Ланцюжок візуалізується в діаграмі Ганта.
3.1 Попередній аналіз трудомісткості процесу розробки ПЗ
Для розробки ефективного плану процесу розробки програмного забезпечення моделювання імпульсного нейронного елемента необхідно скласти попередній план задач, які повинні згодом бути виконаними відповідними працівниками. Для розробки програмного забезпечення моделювання імпульсного нейронного елемента визначимо відповідні задачі та попередній розрахунок часу на їх виконання зазначимо біля кожного пункту плану. Дані зведемо в таблицю 3.1.
Таблиця 3.1 – Задачі та попередній розрахунок часу
|
№ |
Формулювання задачі |
Час, на її виконання, s.p. |
|
1 |
Розробка технічного завдання |
2 s.p. |
|
2 |
Аналіз існуючих методів |
1 s.p. |
|
3 |
Вирішення поставленої задачі |
2 s.p. |
|
4 |
Розробка математичної моделі для вирішення даної задачі |
2 s.p. |
|
5 |
Вибір та узгодження програмного забезпечення |
1 s.p. |
|
6 |
Розробка алгоритму роботи програми |
2 s.p. |
|
7 |
Розробка програмного блоку |
4 s.p. |
|
8 |
Тестування програмного блоку |
2 s.p. |
|
9 |
Виправлення помилок |
1 s.p. |
|
10 |
Додавання нових можливостей |
2 s.p. |
|
11 |
Випуск бета-версії |
2 s.p. |
|
12 |
Відлагодження роботи програмного засобу |
2 s.p. |
|
13 |
Розробка технічної документації |
3 s.p. |
|
14 |
Випуск готового продукту |
1 s.p. |
Для виконання усіх поставлених задач щодо розробки програмного забезпечення необхідні наступні спеціалісти:
- менеджер;
- програміст_1;
- програміст_2;
- тестувальник.
Після того як визначено список необхідних задач та фахівців, необхідних для розробки програмного забезпечення моделювання імпульсного нейронного елемента необхідно розробити план реалізації даного проекту в середовищі Microsoft Project.
На рисунку 3.1 відображено перелік основних задач з терміном їх виконання, а також початковими та кінцевими термінами дії. Відповідно ці ж самі задачі можна переглянути у вигляді діаграми Ганта (рисунок 3.2).
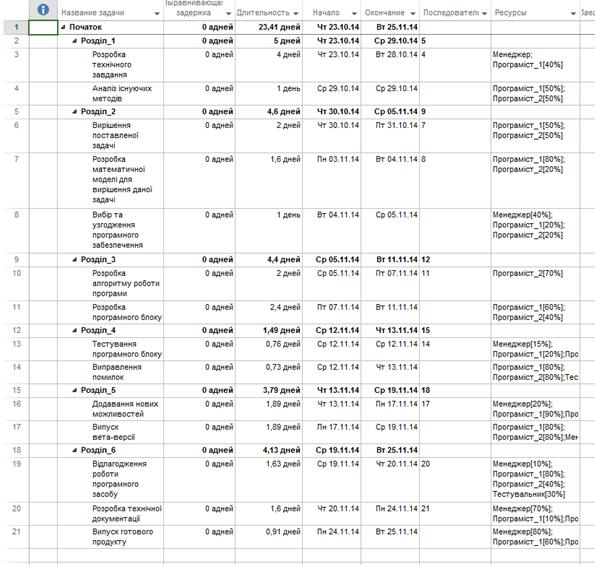
Рисунок 3.1 – Перелік задач для виконання

Рисунок 3.2 – Діаграма Ганта
Отже, після планування процесу розробки програмного забезпечення моделювання імпульсного нейронного елемента отримаємо наступні дані:
- тривалість процесу розробки становить 24 дні;
- затрати становлять 23 108 грн.
Затрати на виробництво продукту загалом, а також затрати на кожного з робітників можна переглянути за допомогою звіту про затрати ресурсів, зображених на рисунку 3.3 та 3.4.

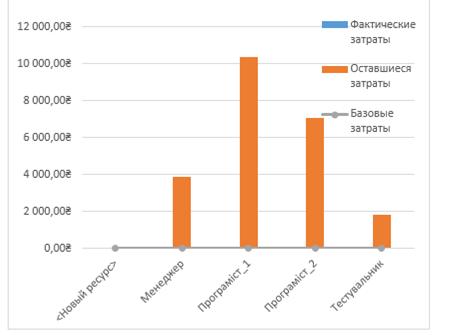
Рисунок 3.3 – Затрати для трудових ресурсів
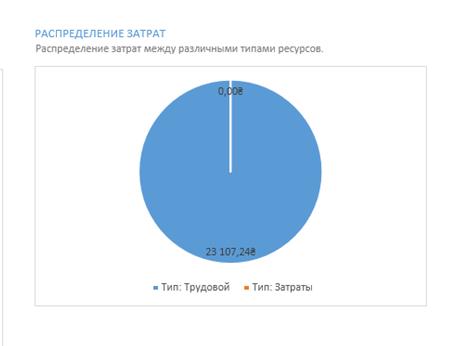
Рисунок 3.4 – Загальні затрати на розробку
3.2 Розробка детального плану розробки ПЗ
В попередній частині було описано планування програмного продукту без врахування обмежень, які можуть впливати на розробку та якість кінцевого програмного продукту і тому саме в даній частині буде використано та враховано ті обмеження, які можуть вплинути на процес розробки програмного продукту.
Основними обмеженнями виступатимуть наступні обмеження, а саме: зменшення фінансування та скорочення терміну виконання проекту. Замовником виставлено конкретні вимоги – це зменшення суми на 5000 грн та скорочення терміну на 3 дні.
Таким чином, після внесення відповідних змін список задач матиме вигляд, який зображений на рисунку 3.5.
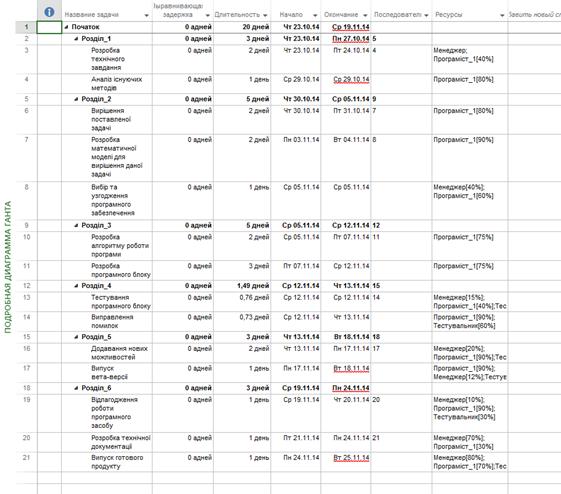
Рисунок 3.5 – Змінений перелік задач для виконання
Здійснення скорочення терміну виконання проекту виконувалося шляхом зменшення розробки технічного завдання на 2 дні та виконання відлагодження роботи програми на 1 день. А зменшення фінансування проекту досягалося шляхом звільнення одного із програмістів і перенаправленням його роботи іншому, тому в результаті вартість проекту зменшилась, що і задовольнило потребам замовника. Діаграма Ганта зображена на рисунку 3.6
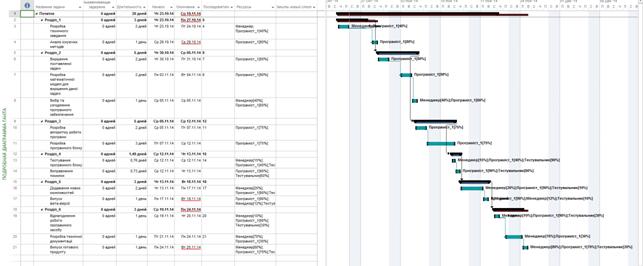
Рисунок 3.6 – Діаграма Ганта із врахуванням обмежень
Отже, після планування процесу розробки програмного забезпечення моделювання імпульсного нейронного елемента з врахуванням можливих обмежень було досягнуто таких результатів:
- термін реалізації проекту зменшився на 3 дні;
- вартість фінансування проекту знизилася на 5000 грн.
Затрати на виробництво продукту загалом, а також затрати на кожного із працюючих над надою розробкою можна переглянути за допомогою наступних відомостей. На рисунку 3.7 зображено затрати для трудових ресурсів на розробку програмного забезпечення моделювання імпульсного нейронного елемента з врахуванням усіх змін, які були спричинені додатковими обмеженнями.
На рисунку 3.8 зображено загальні затрати на розробку програмного забезпечення моделювання імпульсного нейронного елемента з врахуванням введення обмеження фінансування, а саме зменшення загальних витрат на суму близько 5000 грн.

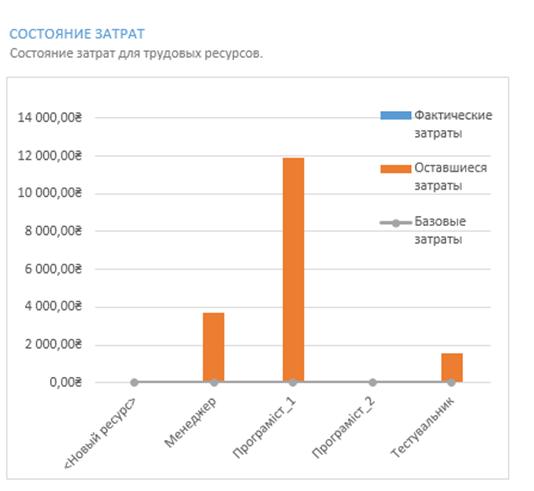
Рисунок 3.7 – Затрати для трудових ресурсів
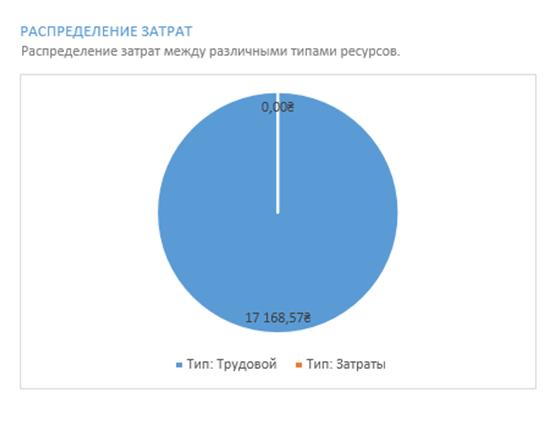
Рисунок 3.8 – Загальні витрати на розробку
3.3 Планування процесу розробки програмного забезпечення моделювання імпульсного нейронного елемента при ідеальних умовах.
Припускається, що на даному етапі планування не існує жодних обмежень ні у фінансовій частині, ні в плані ресурсів, а також немає обмежень, які примушують здати певний продукт в раніше визначені часові проміжки. В такій ситуації збільшимо або зменшимо кількість часу на вирішення основних та окремих задач та додамо ще одного програміста, який буде працювати на рівні із першим основним програмістом.
Отже, змінений порядок задач буде мати наступний вигляд, який представлений на рисунку 3.9. Діаграма Ганта для даного етапу планування зображена на рисунку 3.10.
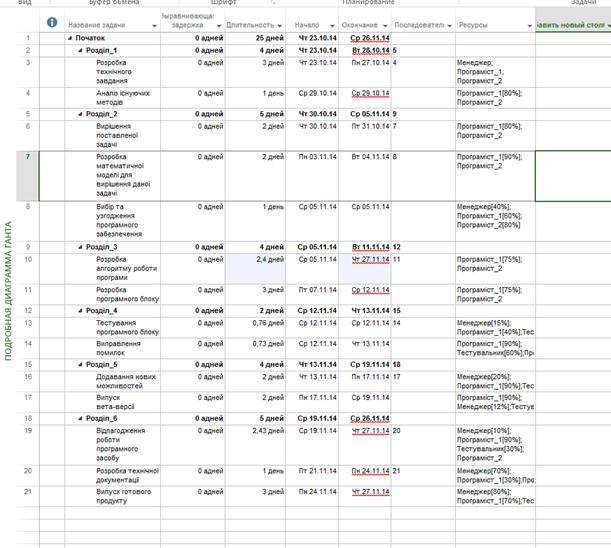
Рисунок 3.9 – Змінений список задач
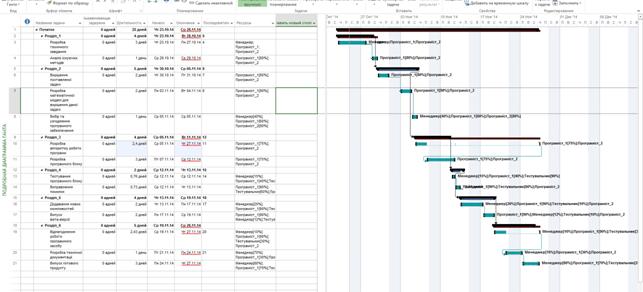
Рисунок 3.10 – Діаграма Ганта
Із даного плану термін здачі проекту збільшився на 5 днів та складає 25 днів. Також завдяки тому, що на роботу було прийнято нового програміста, який працюватиме на кожному етапі разом із попереднім програмістом, ціна реалізації проекту збільшиться на 24000 грн, але в результаті буде якісний програмний продукт, розробку якого також підтримуватиме на кожному із етапів досвідчений програміст.
Діаграми витрат на ресурси та загальні витрати зображено на рисунках 3.11 та 3.12.

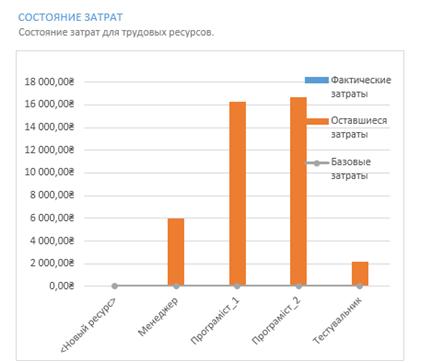
Рисунок 3.11 – Затрати для трудових ресурсів
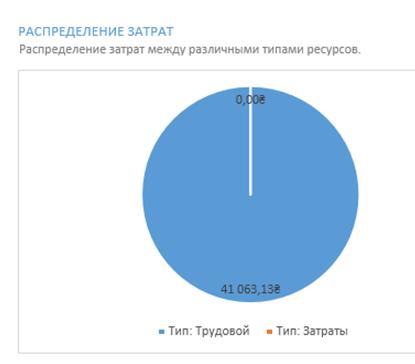
Рисунок 3.12 – Затрати для трудових ресурсів
3.4 Планування процесу розробки програмного забезпечення моделювання імпульсного нейронного елемента з використанням Scrum.
Scrum – це методологія розробки програмного забезпечення, що базується на ітеративній розробці, в якій вимоги та розв"язки весь час змінюєтьс через співпрацю між людьми у команді.
Гнучка розробка – найкращий засіб для підвищення продуктивності розробників програмного забезпечення.
Основою для розробки програмного забезпечення моделювання імпульсного нейронного елемента будуть історії користувачів, що явлють собою елементарні функціональні властивості програмного продукту.
Так, на рисунку 3.13 зображено історії користувачів, які утворюють так званий ProductBacklog. Вона має унікальний номер, пріоритет та час, потрібний на її виконання, який вимірюється в story point.
ProductBacklog
містить усі задачі, які були поставлені під час
планування розробки програмного забезпечення моделювання імпульсного нейронного
елемента від розробки технічного завдання до випуску готового продукту,вказуючи
вищезазначені параметри (номер, пріоритет, час). 
Рисунок 3.13 – ProductBacklog
Із рисунку 3.13 видно, що, наприклад, історія під номером 8, а це – тестування програмного блоку має пріоритет 7 та потребує часу на реалізацію в 2 s.p.
Проект буде розподілений на 4 спрінти. Виникає задача розподілення всіх задач в залежності від їх пріоритету. Також кожна історія розподілена на ще малі задачі, які конкретно мають свій час виконання. Перший спрінт зображений на рисунку 3.14.

Рисунок 3.14 – SprintBacklog (перший спрінт)
Другий спрінт зображений на рисунку 3.15.

Рисунок 3.15 – SprintBacklog (другий спрінт)
Третій спрінт зображений на рисунку 3.16.

Рисунок 3.16 – SprintBacklog (третій спрінт)
Четвертий спрінт зображений на рисунку 3.17.

Рисунок 3.17 – SprintBacklog (четвертий спрінт)
Для виконанн я будь-якого спрінта формується своєрідний план, що містить всі задачі на даний спрінт, задачі що в процесі виконання та задачі які вже вирішені. Також в даному плані позначаються задачі, що не були заплановані й додаткові задачі, у випадку виконання усіх запланованих. Також в даному плані будується графік, що відображає порядок виконання спринта. На рисунку 3.18-3.21 зображено такі плани для усіх чотирьох спринтів відповідно.

Рисунок 3.18 – План реалізації (перший спрінт)
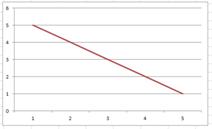
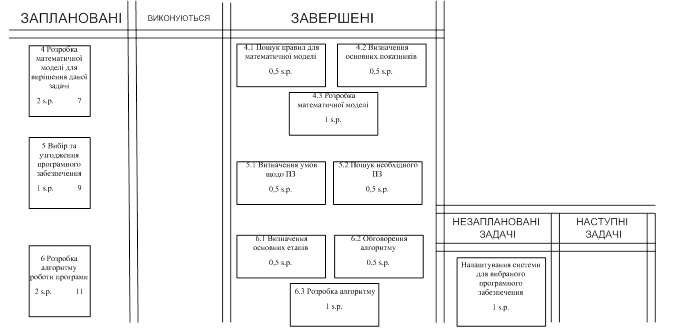
Рисунок 3.19 – План реалізації (другий спрінт)
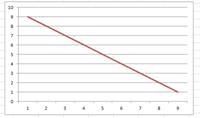
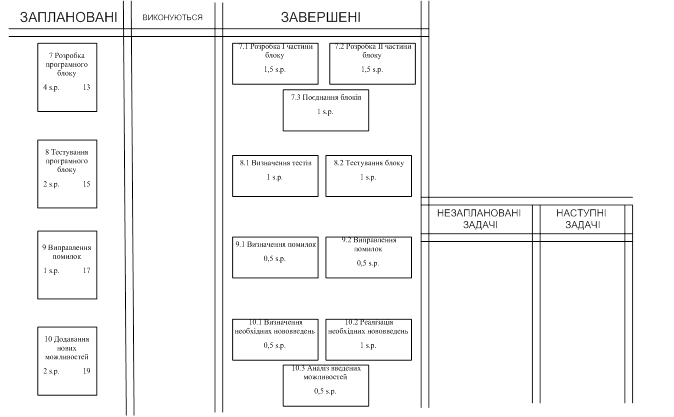
Рисунок 3.20 – План реалізації (третій спрінт)
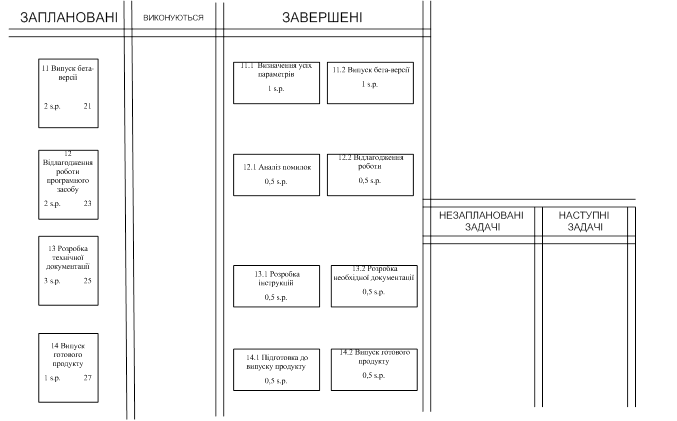
Рисунок 3.21 – План реалізації (четвертий спрінт)
3.5 Висновки до розділу 3
Попередньо визначений порядок дій, необхідних для досягнення поставленої цілі це і є планування. Планування є однією із найголовніших задач при створенні програмного продукту. Microsoft Project – система управління проектами, розроблена корпорацією Microsoft, створена, щоб допомогти менеджерові проекту в розробці планів, розподілі ресурсів за завданнями, відстежуванні прогресу і аналізі обсягів робіт. Scrum – це ітераційний метод планування та керування процесами та проектами. Scrum виділяє короткі цикли розробки продукту – спрінти, надаючи додаткові оновлення в залежності від зміни потреб клієнта.
У даному розділі було розглянуто планування процесу розробки програмного забезпечення моделювання імпульсного нейронного елемента без зовнішніх обмежень. Також розглянуто і з певними зовнішніми обмеженнями й також у ідеальних умовах. Також було спроектовано реалізацію програмного блоку моделювання імпульсного нейронного елемента за допомогою методології Scrum.
4 РОЗРОБКА ПРОГРАМНОГО ЗАБЕЗПЕЧЕННЯ
4.1 Огляд програмного середовища CSIM
CSIM є інструментом для моделювання мереж з різних нейронів і синапсів. Призначений для імітації мереж, що містять до декількох тисяч нейронів і до 1.000.000 синапсів. CSIM розповсюджується під GNU General Public License.
Особливостями середовища є:
- підтримка різних рівнів моделювання;
- простий у використанні інтерфейс Matlab;
- об’єктно-орієнтоване проектування;
- швидке ядро;
- працездатність на багатьох ОС;
- зовнішній інтерфейс.
Circuit Simulator (CSIM) являє собою програмний пакет для моделювання імпульсних нейронних мереж, що складаються з різноманітних моделей нейронів та синапсів. Пакет в першу чергу призначений для розподіленого моделювання великомасштабних мереж, що складаються з великої кількості нейронів (до 10000 нейронів та до кількох млн. синапсів, але реальний максимальний розмір мережі визначається об’ємом оперативної пам’яті комп’ютера). Все обчислювальне ядро [10] написано на мові програмування C++, але основний інтерфейс CSIM здійснено в середовищі програмування Matlab, що є потужним середовищем програмування і дозволяє користувачеві легко інтегрувати нейронний симулятор в програму для аналізу та візуалізації даних для управління нейронними мережами та для моделювання певного завдання.
Особливості пакету програм CSIM. Різні моделі нейрона: leaky-integrate-and-fire нейрони, потокові нейрони, сигмоїдальні нейрони.
Різні моделі синапсів: статичний та динамічний синапси. Тривалість імпульсів залежить від часу синаптичної пластичності, що також реалізовано в програмному пакеті CSIM.
Простий у використанні інтерфейс Matlab. Бібліотека CSIM включена в Matlab, тому немає необхідності вчити будь-які інші мови програмування. Все налаштування параметрів пакету виконується за допомогою скриптів MATLAB. Крім того, всі результати моделювання безпосередньо повертаються у вигляді масиву Matlab тому, будь-які графіки та інструменти аналізу, доступні в Matlab і їх можна легко застосувати.
Об"єктно-орієнтований підхід. Існують об"єкти (наприклад, об"єкт LifNeuron реалізує стандартний клас моделі нейрону) , які з"єднані між собою за допомогою деяких синапсів. Створення об"єктів, з"єднання об"єктів і налаштування параметрів об"єктів контролюється на рівні скриптів Matlab, тоді як фактичне моделювання здійснюється на мові програмування C + + .
Сучасна комп"ютерна математика пропонує цілий набір інтегрованих програмних систем і пакетів програм для автоматизації математичних розрахунків: Eureka, Gauss, TK Solver, Derive.
MatLab — одна з найстарших, ретельно пророблених й перевірених часом систем автоматизації математичних розрахунків, яка побудована на розширеному представленні й застосуванні матричних операцій. Це знайшло відображення в назві системи — MATrix LABoratory — матрична лабораторія. Однак синтаксис мови програмування системи продуманий настільки ретельно, що ця орієнтація майже не відчувається тими користувачами, яких не цікавлять безпосередньо матричні обчислення [11].
Матриці широко застосовуються в складних математичних розрахунках, наприклад, при рішенні задач лінійної алгебри і математичного моделювання статичних і динамічних систем і об"єктів. Вони є основою автоматичного складання й рішення рівнянь стану динамічних об"єктів і систем. Прикладом може служити розширення MATLAB — Simulink. Це істотно підвищує інтерес до системи MATLAB, що увібрала в себе кращі досягнення в області швидкого рішення матричних задач.
Однак MatLab не вийшла за межі спеціалізованої матричної системи і стала однією з найбільш могутніх універсальних інтегрованих обчислювальних систем. Слово «інтегрована» указує на те, що в цій системі об"єднані зручна оболонка, редактор виражень і текстових коментарів, обчислювач і графічний програмний процесор. У новій версії використовуються такі могутні типи даних, як багатомірні масиви, масиви осередків, масиви структур, масиви Java і розріджені матриці, що відкриває можливості застосування системи при створенні й налагодженні нових алгоритмів матричних і заснованих на них рівнобіжних обчислень і великих баз даних.
MatLab — це унікальна колекція реалізацій сучасних чисельних методів комп"ютерної математики, створених за останні три десятки років. Вона увібрала в себе і досвід, правила і методи математичних обчислень, які були накопичені за тисячі років розвитку математики. Це сполучається з могутніми засобами графічної візуалізації і навіть анімаційної графіки. Систему з прикладеної до неї великою документацією цілком можна розглядати як фундаментальний багатотомний електронний довідник з математичного забезпечення ЕОМ — від масових персональних комп"ютерів до супер-ЕОМ. Можливості MatLab дуже великі, а по швидкості виконання задач система нерідко перевершує своїх конкурентів. Вона застосовується для розрахунків практично в будь-якій області науки й техніки. Наприклад, дуже широко використовується при математичному моделюванні механічних пристроїв і систем, зокрема, в динаміці, гідродинаміці, аеродинаміці, акустиці, енергетиці і т.д. Цьому сприяє не тільки розширений набір матричних і інших операцій і функцій, але і наявність пакета розширення (toolbox) Simulink, спеціально призначеного для рішення задач блокового моделювання динамічних систем і пристроїв, а також десятків інших пакетів розширень [12].
У великому й постійно поповнюваному комплексі команд, функцій і прикладних програм системи MatLab містяться спеціальні засоби для електротехнічних і радіотехнічних розрахунків (операції з комплексними числами, матрицями, векторами й поліномами, обробка даних, аналіз сигналів і цифрова фільтрація), обробки зображень, реалізації нейроних мереж, а також засоби, що відносяться до інших нових напрямків науки й техніки. Вони ілюструються безліччю практично корисних прикладів.
Важливими перевагами системи є її відкритість і розширюваність. Більшість команд і функцій системи реалізовані у виді текстових m-файлів. Користувачеві надана можливість створювати не тільки окремі файли, але і бібліотеки файлів для реалізації специфічних задач.
Легкість модифікації системи і можливість її адаптації до рішення специфічних задач науки і техніки привели до створення десятків пакетів прикладних програм (toolbox), які набагато розширили сфери застосування системи.
Однією з проблем сучасної науки є розробка і впровадження в практику методів дослідження функціонування складних систем. До класу складних систем відносять технологічні, виробничі, енергетичні комплекси, системи автоматизації керування й інших об"єктів. Моделювання є одним із найбільш могутніх засобів дослідження подібних систем на сьогоднішній день. Моделювання - один із найбільш розповсюджених засобів вивчення різних процесів і явищ. Моделлю вихідного об"єкта називається представлення об"єкта в деякій формі, відмінної від форми його реального існування. В інженерній практиці модель, звичайно, створюється для:
- проведення на моделі експериментів, які неможливо або складно провести на реальному об"єкті (що надає можливість одержання нових знань про об"єкт);
- прискорення, здешевлення, спрощення і будь-якого іншого удосконалення процесу проектування, що досягається за рахунок роботи з більш простим об"єктом, чим вихідний, тобто з моделлю [13].
Сьогодні відомі і широко використовуються в наукових дослідженнях і інженерній практиці різні типи моделей і численні методи моделювання. Якщо взяти за основу ступінь абстрактності, то можна визначити наступні типи моделей:
- фізичні (натурні) моделі (відтворюють досліджуваний процес із збереженням його фізичної природи і є інструментом фізичного моделювання); - аналогові моделі (заміняють один об"єкт на іншій зі схожими властивостями);
- математичні моделі (абстрактні моделі, існують у формі спеціальних математичних конструкцій).
Під математичним моделюванням розуміють засіб дослідження різних процесів шляхом вивчення явищ, що мають різний фізичний зміст, але описуваних однаковими математичними співвідношеннями [14].
Новітня версія системи MATLAB характеризується новими й важливими можливостями:
- доведене до більш ніж 600 число функцій і команд;
- новий інтерфейс із набором інструментів для керування середовищем;
- поліпшені алгоритми на основі оптимізованої бібліотеки LAPACK;
- прискорені методи інтегральних перетворень;
- нові, більш могутні і точні, алгоритми інтегрування диференціальних
рівнянь і квадратур;
- нові сучасні функції візуалізації: вивід на екран двовимірних зображень, поверхонь і об"ємних фігур у виді прозорих об"єктів;
- нова інструментальна панель Camera для керування перспективою і прискорення виводу графіки за допомогою OpenGL;
- новий інтерфейс для виклику Java-процедур і використання Java-об"єктів безпосередньо з MATLAB;
- нові, сучасні інструменти проектування графічного користувальницького інтерфейсу;
- обробка (регресія, інтерполяція, апроксимація й обчислення основних статистичних параметрів) графічних даних прямо з вікна графіки;
- інтеграція із системами контролю версій коду, такими як Visual Source Safe;
- новий інтерфейс (послідовний порт) для обміну даними із зовнішнім устаткуванням з MATLAB;
- новий пакет керування вимірювальними приладами (Instrument Control ToolBox) для обміну інформацією з приладами, підключеними до Каналу загального користування (GPIB, HP-IB, IEEE-488)
- істотно обновлені пакети розширення, зокрема, нові версії пакета моделювання динамічних систем Simulink 4 і Real Time Workshop 4.
4.2 Розробка моделі нейронного елемента в середовищі CSIM
Моделювання LIF нейрону, на вхід якого подаються імпульсні сигнали через динамічний синапс зображено на рисунку 5.1.
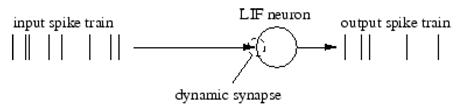
Рисунок 4.1 – Схема модельованого об’єкту
На рис. 4.1 «input spike train» – вхідна послідовність імпульсів; «LIF neuron» – модель LIF нейрону; «Dynamic synapse» – динамічний синапс.
Створення об’єктів відбувається за допомогою команди csim та кодового слова ‘create’:
» i=csim("create","SpikingInputNeuron");
» s=csim("create","DynamicSpikingSynapse");
» n=csim("create","LifNeuron");
SpikingInputNeuron – об’єкт, що генерує вхідну послідовність імпульсів;
DynamicSpikingSynapse – об’єкт, що передає сигнал до нейрону;
LifNeuron – об’єкт, що представляє модель нейрону.
Стандартна LIF-модель нейрону, реалізована так, що мембранний потенціал Vm нейрона подається формулою 4.1:
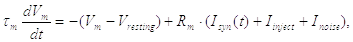 (4.1)
(4.1)
де 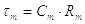 - постійна часу
мембрани, Rm – опір мембрани, Сm – ємність мембрани, Іsyn(t) – струм, що надходить від
синапсів, Іinject – неспецифічний фоновий
струм і Іnoise – Гауссова випадкова величина з нульовим середнім і заданою
дисперсією шуму [15].
- постійна часу
мембрани, Rm – опір мембрани, Сm – ємність мембрани, Іsyn(t) – струм, що надходить від
синапсів, Іinject – неспецифічний фоновий
струм і Іnoise – Гауссова випадкова величина з нульовим середнім і заданою
дисперсією шуму [15].
У момент t=0 Vm встановлюється в Vinit . Якщо потім в результаті дії вхідних сигналів Vm досягає порогову напругу Vthrech , то генерується вихідний імпульс, а Vm скидається до Vreset і утримується таким протягом періоду абсолютної рефрактерності.
З формули 4.1 видно, до LIF-нейрон має багато параметрів, зміна яких призводить до зміни поведінки самого нейрону.
Серед даних параметрів виділяються такі: ємність мембрани, опір мембрани, порогова напруга, потенціал спокою, потенціал скидання (після генерації імпульсу), початковий потенціал (у час t=0), період рефрактерності, струм шумів, постійний вхідний струм (зовнішній), тип нейрону (збуджувальний чи гальмівний).
Модель нейронного елемента виконується в середовищі CSIM, що є частиною програмного засобу MatLab (рисунок 4.2).
Рисунок 4.2 – Загальний вигляд програмного засобу MatLab
Як основу математичної моделі нейронного елементу використовується математична модель, яка була вдосконалена, а саме модель LIF-нейрону. Даний нейрон й програмується в середовищі CSIM. Під час програмування математичної моделі нейронного елементу вказуються й відповідні йому параметри [16].
Програмований вигляд нейронного елементу, що виконаний у визначеному програмному середовищі зображений на рисунку 4.3, де й знаходиться лістинг для забезпечення функціонування нейронного елементу.
Рисунок 4.3 – Нейронний елемент в середовищі CSIM
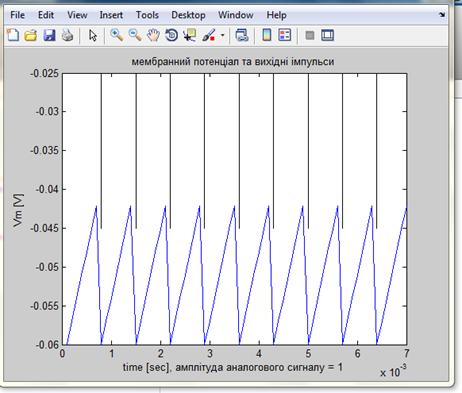
На рисунку 4.4 зображено уже побудовану програмним засобом фігуру, що показує нам мембранний потенціал та відповідно вихідні імпульси.
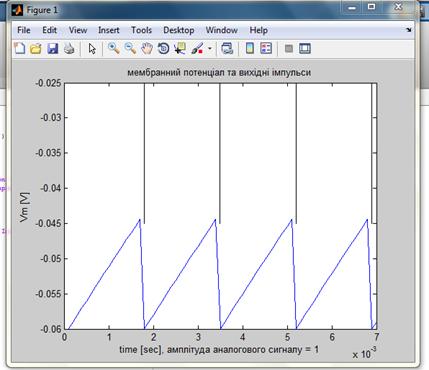
Рисунок 4.4 – Мембранний потенціал та вихідні імпульси нейрону
Для забезпечення аналізу та підтвердження дослідження, що проводиться необхідно виконати запуск даного нейронного елементу із різними значеннями струму та знайти частоту виникнення імпульсів.
ВИСНОВКИ
Під час виконання курсової роботи було проведено аналіз предметної області, де сформовано певну інформацію про існуючі моделі нейронних елементів. Також проведено обґрунтування методу розв’язання задачі, де аргументовано загалом проведення даного дослідження, недосконалість аналогів та наведено інформацію щодо математичної моделі штучного нейронного елементу.
Вдосконалено математичну модель нейронного елемента. Дане дослідження та вдосконалення здійснювалося в середовищі CSIM, що дозволило зробити відповідний аналіз на порівняння передатних характеристик моделі і досягти спрощення реалізації імпульсного нейрону та доведення адекватності даної моделі.
Також було розглянуто планування процесу розробки програмного забезпечення моделювання імпульсного нейронного елемента без зовнішніх обмежень, із певними зовнішніми обмеженнями й також у ідеальних умовах. Було спроектовано реалізацію програмного блоку моделювання імпульсного нейронного елемента за допомогою методології Scrum.
В результаті це відображає, що запропоновану модель імпульсного нейрону можна використовувати для побудови великих нейронних мереж.
ПЕРЕЛІК ПОСИЛАНЬ
1. Бардаченко В.Ф. Основи теорії таймерних обчислювально-вимірювальних пристроїв / В.Ф. Бардаченко, В.М. Кичак - Вінниця: ВНТУ, 2003.-79 с.
2. Пат. 76924 Україна, МПК G 06 G 7/60. Модель нейрона / О. К. Колесницький, Ю. В. Левченко, Г. О. Колесницька, заявник і власник патенту Вінницький нац. технічн. ун-т – № 201207181; заявлено 13.06.12; опубл. 25.01.13, Бюл.№2.
3. Пат. №22956А України. Модель нейрона/ Кожем"яко В.П., Колесницький О.К. Нізельський М.Б., Василецький С.А. Опубл. Бюл. №3, 5.05.98.
4. Колесницький О.К. Частотно-динамічні нейронні елементи / О.К. Колесницький, С.А. Василецький - Вісник ВПІ. 2002. - №5 – С. 5 - 10.
5. Бардаченко В.Ф. Перспективи застосування імпульсних нейронних мереж з таймерним представленням інформації для розпізнавання динамічних образів / В.Ф. Бардаченко О.К. Колесницький, С.А. Василецький - УСіМ. -2003-№6.- С. 73-82.
6. Kolesnytskyj O.K. Optoelectronic BISPIN - based neuron element / O.K. Kolesnytskyj, S.A. Vasyletskyy - Вінниця, 2000. – С. 81–82.
7. Кичак В.М. Визначення допоміжних сигналів для синтезу частотних елементів з трійковим структурним алфавітом В.М. Кичак, В.Ф. Бардаченко Вимірювальна та обчислювальна техніка в технологічних процесах, 2001, №1, с.101-105.
8. Пат. №22956А України. Модель нейрона/ Кожем"яко В.П., Колесницький О.К. Нізельський М.Б., Василецький С.А. Опубл. Бюл. №3, 5.05.98.
9. Соколов Е.Н. Нейробионика, организация нейроподобных элементов и систем / Е.Н. Соколов, Л.А. Шмелев - М.Наука, 1983. - 279 с.
10. C. Mead, “Neuromorphic electronic systems, / C. Mead, Proc. IEEE, vol. 78, pp. 1629–1636, 1990.
11. Куссуль Э.М. Ассоциативные нейроподобные структуры / Э.М.Куссуль – К.: Наукова думка, 1990. - 235 с.
12. Мартинюк Т.Б. Аналіз та оптимізація складних систем: Навчальний посібник / Т.Б. Мартинюк, В.П. Кожем’яко. - Вінниця: ВДТУ, 1998. - 79 с.
13. Ткаченко Р.О. Нова парадигма штучних нейронних мереж прямого поширення / Р.О. Ткаченко - Вісник Державного університету “Львівська політехніка”: Комп’ютерна інженерія та інф. технології. –1999, №386. - С.43-54.
14. Колесницький О.К., Левченко Ю.В. Система комп’ютерного моделювання нейронного елементу на основі стабілітрону/ О. К. Колесницький, Ю.В. Левченко // Інтелектуальні технології в системному програмуванні: всеукр. наук.-практ. конф., 23-23 квітня 2014 р.: тези доповіді – Хмельницький, 2014. – с.287.
15. Колесницький О.К. Експериментальні дослідження оптоелектронних імпульсних нейронних елементів на біспін-приладі / О.К. Колесницький, С. А. Василецький - Вісник ВПІ. - 2003. - №4. – C. 24-27.
16. Василецький С.А. Математичне та комп’ютерне моделювання оптоелектронного частотно-динамічного нейронного елемента / О.К. Колесницький, С.А. Василецький - Оптоелектронні інформаційно-енергетичні технології.-2001.-№2.-с. 96-101.
Додаток А
Міністерство освіти і науки України
Вінницький національний технічний університет
Інститут інформаційних технологій та комп’ютерної інженерії
ЗАТВЕРДЖУЮ
Зав. каф. КН, д.т.н., проф.
_____________ С.І.Перевозніков
«__» _____________ 2014 р.
ТЕХНІЧНЕ ЗАВДАННЯ
На програмний засіб вдосконалення метематичної
моделі нейронного елемента
1. Найменування й область застосування
Робоча назва програмного комплексу, що розробляється – «Вдосконалення математичної моделі для програмного засобу нейронного елемента».
Розробка математичної моделі програмного забезпечення нейронного елемента може бути прикладом використання її для побудови великої кількості нейронних мереж. Програмна складова курсової роботи буде використана в навчальних цілях при розробці дипломної роботи.
2. Підстави для розробки
Завдання на курсову роботу, протокол засідання кафедри КН № від 2014 року.
3. Мета та призначення розробки
Основною метою роботи є проведення теоретичного та практичного дослідження нейронного елемента, її математичної моделі, удосконалення математичної моделі нейронного елемента, а також розробка програмного забезпечення.
4. Вимоги до програмного забезпечення
4.1. Вимоги до функціональних характеристик:
· мова програмування та середовище розробки повинні забезпечити маніпулювання та обробку даних;
· можливість отримання передатних характеристик, які слугуватимуть для отримання аналізу.
4.2. Вимоги до програмного середовища
Програма повинна бути розроблена в спеціалізованому програмному середовищі розробки CSIM, що є над додатком середовища MATLAB. Це середовище надає широкі можливості для розробки та володіє дружнім по відношенню до програміста інтерфейсом.
5. Вимоги до інформаційної і програмної сумісності
Для успішного запуску програми необхідна наявність персонального комп"ютера із встановленою програмним середовищем MATLAB.
6. Вимоги до технічного забезпечення
Для ефективної роботи програми необхідний ПК з наступними мінімальними характеристиками:
– тактова частота процесора 1,8ГГц;
– об’єм оперативної пам’яті 512 МБ;
– об’єм фізичної пам’яті – 1 ГБ;
– графічний адаптер SVGA з об’ємом оперативної пам’яті 256 МБ.
7. Додаткові вимоги
Для роботи з ПК до кваліфікації користувачів не пред’являється особливих вимог.
Додаток Б
Інструкція користувача
1. Для запуску необхідна наявність програмного засобу MATLAN R2013.

Рисунок Б.1 – Загальний вигляд програмного засобу MatLab
2. Встановлене додаткове середовище СSIM, в якому натискачи кнопку «Run», запускається дана програма.

Рисунок Б.2 – Програмний код в середовищі CSIM
Додаток В
Мембранний потенціал та вихідні імпульси
математичної моделі нейрону

Додаток Г
Лістинг програми
clear all
close all
addpath("C:LabYuraCsimlsmcsim");
clear all
addpath("..");
i=csim("create","AnalogInputNeuron");
s=csim("create","StaticAnalogSynapse");
n=csim("create","LifNeuron");
%csim("set","randSeed",123456);
csim("set",n,"Trefract",0.00002,"Inoise",0);
csim("set",s,"W",2e-6);
csim("connect",n,s);
csim("connect",s,i);
r=csim("create","Recorder");
csim("set",r,"dt",0.1e-3);
csim("connect",r,s,"psr");
csim("connect",r,n,"Vm");
csim("connect",r,n,"spikes");
Tsim=0.007;
stimulusIntensity = 0.1;
S.spiking = 0;
%S.dt = 0.5e-3;
S.dt = NaN;
S.idx = i;
%S.data = stimulusIntensity*ones(0:S.dt:Tsim);
S.data = stimulusIntensity;
csim("simulate",Tsim,S);
t=csim("get",r,"traces");
figure(1); clf reset;
% subplot(3,1,1);
% plot(0:S.dt:Tsim,S.data,"r-")
% %st=S.data;
% %line([st; st],[-0.045; -0.015]*ones(size(st)),"Color","k");
% set(gca,"Xlim",[0 Tsim]);
% title("Вхідний сигнал");
% axis off
%
% subplot(3,1,2);
% plot(t.channel(1).dt:t.channel(1).dt:Tsim,t.channel(1).data)
% ylabel([t.channel(1).fieldName " [A]"]);
% title("postsynaptic response");
%
% subplot(3,1,3);
plot(t.channel(2).dt:t.channel(2).dt:Tsim,t.channel(2).data)
st=t.channel(3).data;
line([st; st],[-0.045; -0.025]*ones(size(st)),"Color","k");
ylabel([t.channel(2).fieldName " [V]"]);
xlabel("time [sec], амплітуда аналогового сигналу = 1");
title("мембранний потенціал та вихідні імпульси");
drawnow;
clear all
close all
addpath("C:LabYuraCsimlsmcsim");
clear all
addpath("..");
i=csim("create","AnalogInputNeuron");
s=csim("create","StaticAnalogSynapse");
n=csim("create","LifNeuron");
%csim("set","randSeed",123456);
csim("set",n,"Trefract",0.00002,"Inoise",0);
csim("set",s,"W",2e-6);
csim("connect",n,s);
csim("connect",s,i);
r=csim("create","Recorder");
csim("set",r,"dt",0.1e-3);
csim("connect",r,s,"psr");
csim("connect",r,n,"Vm");
csim("connect",r,n,"spikes");
Tsim=0.007;
stimulusIntensity = 0.2;
S.spiking = 0;
%S.dt = 0.5e-3;
S.dt = NaN;
S.idx = i;
%S.data = stimulusIntensity*ones(0:S.dt:Tsim);
S.data = stimulusIntensity;
csim("simulate",Tsim,S);
t=csim("get",r,"traces");
figure(1); clf reset;
% subplot(3,1,1);
% plot(0:S.dt:Tsim,S.data,"r-")
% %st=S.data;
% %line([st; st],[-0.045; -0.015]*ones(size(st)),"Color","k");
% set(gca,"Xlim",[0 Tsim]);
% title("Вхідний сигнал");
% axis off
%
% subplot(3,1,2);
% plot(t.channel(1).dt:t.channel(1).dt:Tsim,t.channel(1).data)
% ylabel([t.channel(1).fieldName " [A]"]);
% title("postsynaptic response");
%
% subplot(3,1,3);
plot(t.channel(2).dt:t.channel(2).dt:Tsim,t.channel(2).data)
st=t.channel(3).data;
line([st; st],[-0.045; -0.025]*ones(size(st)),"Color","k");
ylabel([t.channel(2).fieldName " [V]"]);
xlabel("time [sec], амплітуда аналогового сигналу = 1");
title("мембранний потенціал та вихідні імпульси");
drawnow;
clear all
close all
addpath("C:LabYuraCsimlsmcsim");
clear all
addpath("..");
i=csim("create","AnalogInputNeuron");
s=csim("create","StaticAnalogSynapse");
n=csim("create","LifNeuron");
%csim("set","randSeed",123456);
csim("set",n,"Trefract",0.00002,"Inoise",0);
csim("set",s,"W",2e-6);
csim("connect",n,s);
csim("connect",s,i);
r=csim("create","Recorder");
csim("set",r,"dt",0.1e-3);
csim("connect",r,s,"psr");
csim("connect",r,n,"Vm");
csim("connect",r,n,"spikes");
Tsim=0.007;
stimulusIntensity = 0.3;
S.spiking = 0;
%S.dt = 0.5e-3;
S.dt = NaN;
S.idx = i;
%S.data = stimulusIntensity*ones(0:S.dt:Tsim);
S.data = stimulusIntensity;
csim("simulate",Tsim,S);
t=csim("get",r,"traces");
figure(1); clf reset;
% subplot(3,1,1);
% plot(0:S.dt:Tsim,S.data,"r-")
% %st=S.data;
% %line([st; st],[-0.045; -0.015]*ones(size(st)),"Color","k");
% set(gca,"Xlim",[0 Tsim]);
% title("Вхідний сигнал");
% axis off
%
% subplot(3,1,2);
% plot(t.channel(1).dt:t.channel(1).dt:Tsim,t.channel(1).data)
% ylabel([t.channel(1).fieldName " [A]"]);
% title("postsynaptic response");
%
% subplot(3,1,3);
plot(t.channel(2).dt:t.channel(2).dt:Tsim,t.channel(2).data)
st=t.channel(3).data;
line([st; st],[-0.045; -0.025]*ones(size(st)),"Color","k");
ylabel([t.channel(2).fieldName " [V]"]);
xlabel("time [sec], амплітуда аналогового сигналу = 1");
title("мембранний потенціал та вихідні імпульси");
drawnow;
clear all
close all
addpath("C:LabYuraCsimlsmcsim");
clear all
addpath("..");
i=csim("create","AnalogInputNeuron");
s=csim("create","StaticAnalogSynapse");
n=csim("create","LifNeuron");
%csim("set","randSeed",123456);
csim("set",n,"Trefract",0.00002,"Inoise",0);
csim("set",s,"W",2e-6);
csim("connect",n,s);
csim("connect",s,i);
r=csim("create","Recorder");
csim("set",r,"dt",0.1e-3);
csim("connect",r,s,"psr");
csim("connect",r,n,"Vm");
csim("connect",r,n,"spikes");
Tsim=0.007;
stimulusIntensity = 0.4;
S.spiking = 0;
%S.dt = 0.5e-3;
S.dt = NaN;
S.idx = i;
%S.data = stimulusIntensity*ones(0:S.dt:Tsim);
S.data = stimulusIntensity;
csim("simulate",Tsim,S);
t=csim("get",r,"traces");
figure(1); clf reset;
% subplot(3,1,1);
% plot(0:S.dt:Tsim,S.data,"r-")
% %st=S.data;
% %line([st; st],[-0.045; -0.015]*ones(size(st)),"Color","k");
% set(gca,"Xlim",[0 Tsim]);
% title("Вхідний сигнал");
% axis off
%
% subplot(3,1,2);
% plot(t.channel(1).dt:t.channel(1).dt:Tsim,t.channel(1).data)
% ylabel([t.channel(1).fieldName " [A]"]);
% title("postsynaptic response");
%
% subplot(3,1,3);
plot(t.channel(2).dt:t.channel(2).dt:Tsim,t.channel(2).data)
st=t.channel(3).data;
line([st; st],[-0.045; -0.025]*ones(size(st)),"Color","k");
ylabel([t.channel(2).fieldName " [V]"]);
xlabel("time [sec], амплітуда аналогового сигналу = 1");
title("мембранний потенціал та вихідні імпульси");
drawnow;
clear all
close all
addpath("C:LabYuraCsimlsmcsim");
clear all
addpath("..");
i=csim("create","AnalogInputNeuron");
s=csim("create","StaticAnalogSynapse");
n=csim("create","LifNeuron");
%csim("set","randSeed",123456);
csim("set",n,"Trefract",0.00002,"Inoise",0);
csim("set",s,"W",2e-6);
csim("connect",n,s);
csim("connect",s,i);
r=csim("create","Recorder");
csim("set",r,"dt",0.1e-3);
csim("connect",r,s,"psr");
csim("connect",r,n,"Vm");
csim("connect",r,n,"spikes");
Tsim=0.007;
stimulusIntensity = 0.5;
S.spiking = 0;
%S.dt = 0.5e-3;
S.dt = NaN;
S.idx = i;
%S.data = stimulusIntensity*ones(0:S.dt:Tsim);
S.data = stimulusIntensity;
csim("simulate",Tsim,S);
t=csim("get",r,"traces");
figure(1); clf reset;
% subplot(3,1,1);
% plot(0:S.dt:Tsim,S.data,"r-")
% %st=S.data;
% %line([st; st],[-0.045; -0.015]*ones(size(st)),"Color","k");
% set(gca,"Xlim",[0 Tsim]);
% title("Вхідний сигнал");
% axis off
%
% subplot(3,1,2);
% plot(t.channel(1).dt:t.channel(1).dt:Tsim,t.channel(1).data)
% ylabel([t.channel(1).fieldName " [A]"]);
% title("postsynaptic response");
%
% subplot(3,1,3);
plot(t.channel(2).dt:t.channel(2).dt:Tsim,t.channel(2).data)
st=t.channel(3).data;
line([st; st],[-0.045; -0.025]*ones(size(st)),"Color","k");
ylabel([t.channel(2).fieldName " [V]"]);
xlabel("time [sec], амплітуда аналогового сигналу = 1");
title("мембранний потенціал та вихідні імпульси");
drawnow;













 (zip - application/zip)
(zip - application/zip)











