Устойчивость нелинейных управляемых систем.

Устойчивость нелинейных управляемых систем.

Применение прямого метода Ляпунова.

1. Об одном классе нелинейных управляемых систем. Мы будем рассматривать собственные колебания нелинейной управляемой системы, описываемой следующими дифференциальными уравнениями: (6.1)

                

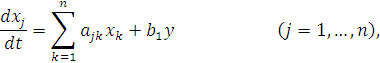
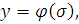
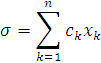
где функция 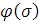 удовлетворяет условию

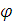(0) = 0.                                       (6.2)

Систему уравнений (1) можно переписать так:

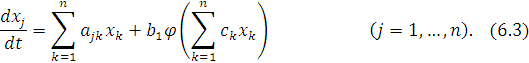
Если ввести матрицы

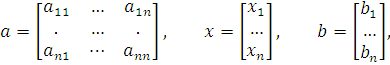
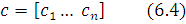
и обозначить через D оператор дифференцирования по времени

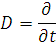
то можно заменить систему дифференциальных уравнений (3) векторным уравнением

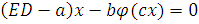        (6.5)

где через Е обозначена единичная матрица.

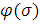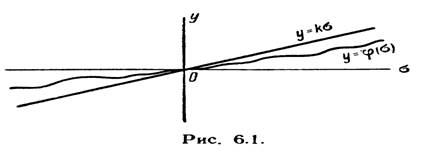
В дополнение к условию (2) будем считать, что функция  такова, что ее график не выходит из угловой области, показанной на рис. 6.1, то есть (6.6)

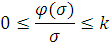
Рис. 6.1.

При k = 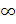 условие (6) сводится к неравенству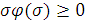     

При b = 0 векторное уравнение (5) принимает вид

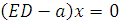    (6.7)

Дифференциальному уравнению (7) соответствует характеристическое уравнение

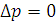, (6.8)

где

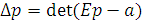 (6.9)

Случай, когда все корни характеристического уравнения (8) расположены на плоскости комплексного переменного р левее мнимой оси, то есть

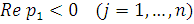
будем называть основным случаем. Ниже мы ограничимся

рассмотрением лишь основного случая.

    Систему уравнений (1) можно в векторной форме записать так:

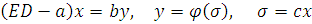     (6.10)

Исключая x из уравнений (10), получим следующее уравнение:

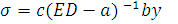(6.11)

Обозначим теперь

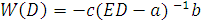 (6.12)

Уравнение (11) примет вид

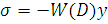 (6.13)

Maтpицa W(D) может быть записана так:

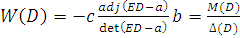   (6.14)

Из выражения (14) видно, что функция W(D) представляет собой скалярную дробно-рациональную функцию, у которой степень числителя ниже степени знаменателя.

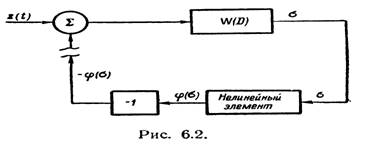
2. Интерпретация функции W(D). Управляемой системе, собственные колебания которой описываются уравнениями (1), можно поставить в соответствие структурную схему, изображенную на рис. 6.2. Схема на рис. 6.2 представляет собой замкнутую управляемую систему, у которой в цепь обратной связи включен нелинейный элемент. Через z(t) обозначен входной сигнал. Рассматриваемая схема будет описываться уравнением

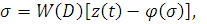 (6.15)

откуда следует, что

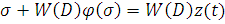. (6.16)

В частном случае, когда

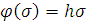 (6.17)

Нелинейный элемент Рис. 6.2.

уравнение (16) принимает следующий вид:

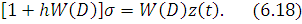
или

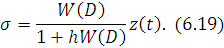
Так как согласно (14)

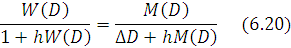
TO уравнение (19) можно переписать так:

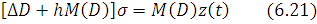
Собственные колебания замкнутой управляемой системы при 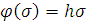  будут описываться однородным уравнением, которое получается из уравнения (21) при :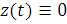

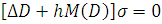 (6.22)

Характеристическое уравнение, соответствующее дифференциальному уравнению (22), будет следующим:

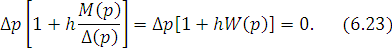
В рассматриваемом здесь основном случае все нули полинома 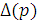 расположены в левой полуплоскости комплексного переменного р. Поэтому для того, чтобы при 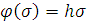замкнутая управляемая система была асимптотически устойчивой, то есть характеристическое уравнение (23) не имело корней

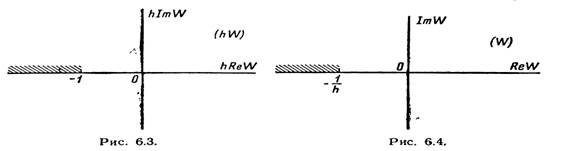
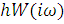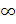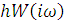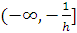
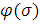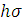В правой полуплоскости достаточно в соответствии с критерием Найквиста, чтобы годограф вектора  не пересекал полуотрезка (-, -1] (рис. 6.3), или годограф вектора не пересекал полуотрезка   (рис. 6.4). Так как функции  удовлетворяют условию (6), то принадлежащие к этому классу линейные функции  удовлетворяют условию 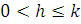, или

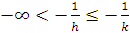 (6.24)

Поэтому для того, чтобы замкнутая управляемая система была асимптотически устойчивой при любой функции 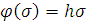, где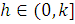

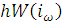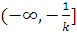необходимо и достаточно, чтобы годограф вектора не пересекал полуотрезка (рис. 6.5).

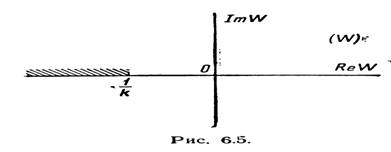
В случае, когда 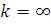, имеем 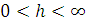, то есть запретной зоной будет интервал (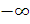,0). Само начало координат в запретную зону не включается, ибо мы рассматриваем функции 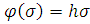 с любым, сколь угодно большим, но конечным значением h.

3. Видоизмененная частотная характеристика. Выше при помощи соотношения (14) была введена функция

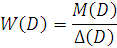
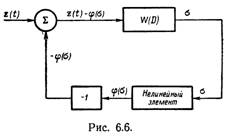
Разомкнем цепь обратной связи у системы, изображенной на рис. 6.2. Разомкнутая система (рис. 6.6) будет описываться уравнением

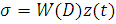 (6.25)

где через z(t) обозначен сигнал, поданный на вход системы.

Как следует из уравнения (25), функция W(D) представляет собой передаточную функцию разомкнутой системы, показанной на рис. 6.6. В соответствии с выражением (14) частотная характеристика разомкнутой системы будет

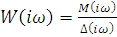  (6.26)

Введем теперь функцию W*(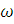), определяемую следующими

соотношениями:

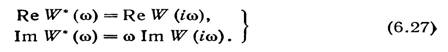
Таким образом, функция W*(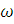) будет иметь вид

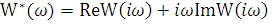 (6.28)

Так как Re W(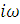) является четной функцией от со, а Im W()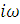

является нечетной функцией от со, то в соответствии с (27)

функция Im W* (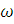) будет четной функцией от 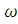 и, таким образом

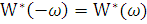
Функция 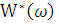называется видоизмененной частотной характеристикой.

Так как в соответствии с (14) функция W(D) представляет собой дробно-рациональную функцию, степень числителя у которой ниже степени знаменателя, то для W(p) будем иметь следующее выражение:

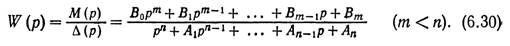
В знаменателе выражения (30) коэффициент при равен единице, так как согласно (9)

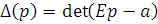
Полагая р = i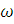, получим согласно (30) что

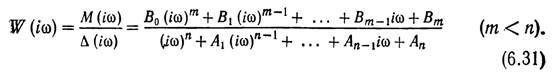
Из выражения (31) следует, что

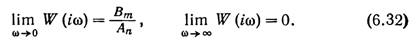
Умножая левую и правую части выражения (31) на 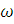, получим

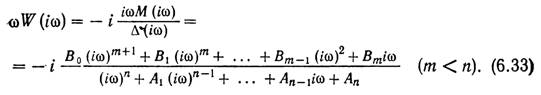
Учитывая, что в соответствии с (27)

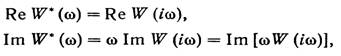найдем, что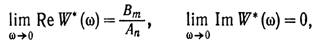

И, следовательно,

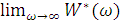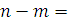Значение  будет различным в случае, когда 1

, и в случае, когда 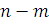 > 1.

При 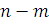 = 1, то есть при 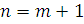, будем согласно (31) и (33) иметь

 

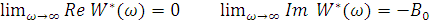
При 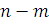 > 1, то есть при 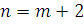, , 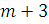,.. , будем иметь

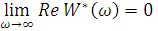
Таким образом,

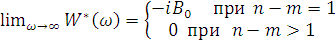      (6.35)

4. Теорема В.-М. Попова. Определение. Систему (1)

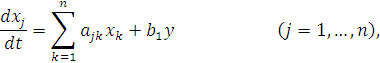
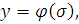
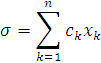
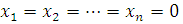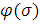тривиальное решение которой асимптотически устойчиво при любых видах функции ,удовлетворяющих условию (6)

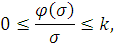
будем называть абсолютно устойчивой в угле .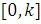

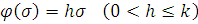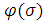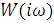Так как линейные функции  входят в число допустимых условием (6) функций, то требование, чтобы годограф вектора  не пересекал полуотрезка 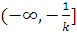 (рис. 6.5), является необходимым условием абсолютной устойчивости системы (1). Достаточное условие абсолютной устойчивости дает теорема В.-М. Попова.

Теорема В.-М. Попова. Для того чтобы система (1) была

абсолютно устойчива в угле 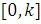, достаточно, чтобы существовало такое конечное действительное число q, при котором для всех значений 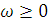 выполнялось условие

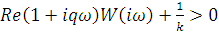      (6.36)