Министерство образования Республики Беларусь
БЕЛОРУССКИЙ НАЦИОНАЛЬНЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
Инженерно-педагогический факультет
Кафедра «Вакуумная и компрессорная техника»
КУРСОВАЯ РАБОТА
по дисциплине «Пневматические устройствам и системы»
РАСЧЕТ ТИПОВОГО ПНЕВМОПРИВОДА
Выполнил
Шитик В. А.
Руководитель
Суша Ю. И.
Минск 2016
СОДЕРЖАНИЕ
ВВЕДЕНИЕ. 3
1.ДИНАМИЧЕСКИЙ СИНТЕЗ ТИПОВОГО ДВУХСТОРОННЕГО ПНЕВМОПРИВОДА.. 4
1.1. Условия получения установившегося движения поршня. 4
1.2. Выбор параметров привода по заданной скорости поршня. 7
1.3. Выбор параметров элементов пневмолиний. 10
2.ДИНАМИЧЕСКИЙ АНАЛИЗПНЕВМОПРИВОД НАГРУЖЕННОГО ПОСТОЯННЫМИ СИЛАМИ.. 12
2.1. Анализ циклограммы типового пневмопривода. 12
2.2. Подготовительный период работы пневмопривода. 14
2.3. Период движения поршня. 20
ЗАКЛЮЧЕНИЕ. 26
СПИСОК ЛИТЕРАТУРЫ.. 27
ВВЕДЕНИЕ
Пневматические приводы получили широкое применение при автоматизации производственных процессов в общем машиностроении, в станкостроении, в литейном и кузнечном производстве.
Пневмоустройства используют в качестве приводов зажимных и транспортирующих механизмов, для дистанционного управления и регулирования, в контрольно-измерительных приборах, при автоматизации машин и устройств, работающих в агрессивных средах, в условиях пожаро- и взрывоопасности, радиации, а также при значительной вибрации и высоких температурах.
Широкое применение пневмоприводов объясняется их преимуществами по сравнению с другими, в первую очередь надежностью функционирования, простотой конструкции, сравнительной легкостью их эксплуатации и обслуживания. Они относительно дешевы и являются средством автоматизации производственных процессов.
Пневмоприводы следует применять в тех случаях, когда требуется обеспечить высокие скорости движения рабочего органа при относительно небольших рабочих усилиях Основными типами исполнительных пневмоустройств, устанавливаемых в машинах, станках и автоматических линиях, являются пневмоцилиндры общепромышленного назначения. С их помощью достигаются относительно высокие скорости (1-3 м/с), что имеет большое значение для повышения производительности машин-автоматов, автоматических линий при выполнении вспомогательных операций (транспортировка, зажим, подача и т.д.). Диаметр пневмоприводов колеблется от 0,01 до 0,3 м, ход поршня от нескольких миллиметров до 2-3 м при самых разнообразных конструктивных исполнениях.
Срок службы пневмоцилиндров доведен до 10 млн. ходов. Давление питания в исполнительных пневмоустройствах обычно равно давлению сжатого воздуха в заводской сети (0,4-1МПа).
1 ДИНАМИЧЕСКИЙ СИНТЕЗ ТИПОВОГО ДВУХСТОРОННЕГО ПНЕВМОПРИВОДА
1.1 Условия получения установившегося движения поршня
Расчетная схема типового двухстороннего пневмопривода возвратно-поступательного движения приведена на рис.1.1.
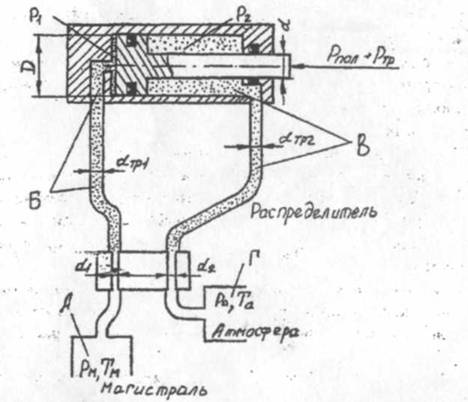
Рисунок 1.1.– Расчетная схема двухстороннего возвратно-поступательного движения
Основной задачей проектного расчета пневмопривода является выбор эффективной площади поршня и эффективных проходных сечений каналов подводящей fэи выхлопной fвэ магистралей по заданной скорости поршня, принимаемой постоянной и при постоянной силе сопротивления. При этом, необходимо учесть особенности пневмопривода, заключающиеся в том, что движение, близкое к установившемуся, может быть получено только при определенных сочетаниях исходных величин, задаваемых конструктору, а именно: средняя скорость поршня Vср, его ход S, масса подвижный частей mn и принимаемых им начальных условиях.
Такими начальными условиями являются:
1) давление в полости наполнения равно атмосферному, а в полости выхлопа - магистральному;
2) давление в общих полостях атмосферное.
Условия первого вида в общей мере способствует получению движения, близкого к равномерному.
Поэтому вначале необходимо оценить возможность получения движения, близкого к равномерному при заданных исходных параметрах.
Изменение скорости определяется значениями безразмерных параметров N, Ω, χ.
Безразмерный конструктивный парaмeтp N, равен
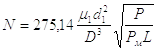 (1.1)
(1.1)
где µ1-коэффициент расхода выхлопной магистрали
d1 - диаметр выхлопной магистрали (м)
D - диаметр поршня (м)
Р - полная сила сопротивления на штоке (Н)
Рм - магистральное давление (МПа)
L - ход поршня (м)
Безразмерный параметр, характеризующий пропускные способности подводящей к выхлопной магистралей Ω, равен:
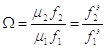
(1.2)
где, соответственно µ1,µ2- коэффициенты расходов подводящей ивыхлопной магистралей; f2 и f1 - площади их сечения.
Безразмерный параметр, характеризующий нагрузку на штоке 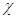 ,равен:
,равен:
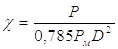 (1.3)
(1.3)
С достаточной для расчетов точностью, условие получения режима движения, близкого к установившемуся, можно записать в виде:
δ≤δу (1.4)
где δ - критерий инерционности пневмопривода, численно равен:
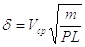 (1.5)
(1.5)
где m - масса всех подвижных частей пневмопривода (поршня, штока и т.д.).
На основании опытных данных установлено граничное значение δу, при превышении которого невозможно получить движение поршня, близкое к установившемуся.
Для начальных условий по давлению в полостях 1-го вида в качестве такой границы допустимо принять δу =0,25и тогда условие получения установившегося движения запишется в виде:
δу<0,25
При использовании выражения (2.5) следует иметь в виду, что величины m и Р, которые представляют собой соответственно полную массу всех подвижных частей и полную силу сопротивления, приложенную к поршню, до выбора диаметра цилиндра и штока конструктору неизвестны. Рекомендуется, предварительно принимать значение массы m≈100-200 кг.
В общем случае полная сила сопротивления равна:
P=P1+P2+P3±PaFш
где P1 - сила трения в уплотнениях поршня и штока
Р2 - сила полезного сопротивления
Рз - вес поршня со штоком (учитывается только для вертикально расположенных пневмоцилиндров. При проектном расчете)
PaFш - сила противодействия в выхлопной полости.
При проектном расчете, можно PaFш≈0
Когда сила полезного сопротивления Р2 является доминирующей, то длярасчета Р1 , можно пользоваться следующей эмпирической зависимостью:
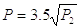 (1.6)
(1.6)
С учетом выражения (2.6), для пневмоцилиндра, расположенного горизонтально, получим:
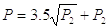 (1.7)
(1.7)
Оценить возможность использования пневмопривода для перемещения массы 136 кг со скоростью Vcp=0,8 м/с на расстояние L=0,8м. Сила полезного сопротивления Р2=258 Н, Определить максимальное значение Vcp из условия сохранения режима равномерного движения:
По формуле (1.9) определим полную силу сопротивления Р
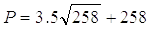
P=314,218H
По формуле (1.5) определим критерий инерционности пневмопривода δ:
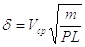 ;
;
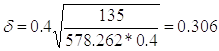
0.5 5<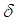 <0.75 =>
<0.75 =>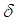 =0.75 –
область режимов переходного типа между установившемся и равноускоренным
движением.
=0.75 –
область режимов переходного типа между установившемся и равноускоренным
движением.
Vср.max=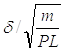 ;
;
Vср.max=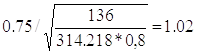 м/с
м/с
Для определения максимального значения Vср.maxпри котором условие Vcp ≈Vp еще будет сохраняться, необходимо левую часть выражения (1.5) приравнять к δp=0,75.
В результате получим Vср.max= 1,02 м/с.
1.2. Выбор параметров привода по заданной скорости поршня
Задача выбора параметров пневмопривода по заданной скорости Vср, и силе сопротивления Р в общем случае не решается однозначно. Задав, например, произвольным значение площади поршня F, которое должно быть больше минимального значения, определяемого из условия получения достаточной движущей силы для преодоления сил сопротивления, можно настроить привод на заданную скорость поршня путем подбора эффективных проходных сечений на входе fэ и выходе fвэ. При этом для каждого F будет иметь не один, а несколько вариантов, характеризуемых различными соотношениями fэ и fBэ.
Количественные отношения F, fэ, fвэмежду определяются безразмерными зависимостями:
– безразмерная эффективная площадь проходного сечения подводящей линии
Uу=fэа1 (1.10)
– коэффициент пропорциональности;
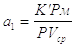 (1.11)
(1.11)
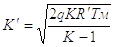 (1.12)
(1.12)
Если принять
Тm=290К, q=9,8 м/с2,
К=1,4 иR=29,3 м/К, то получим:
К=763,5м/с
– безразмерная площадь поршня

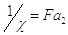 (1.13)
(1.13)
– коэффициент пропорциональности
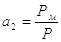 (1.14)
(1.14)
При подсчете a1 и а2давление следует измерять в н/м2 (Па), силу Р в кг м/с2 (Н), скорость - в м/с.
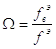
безразмерная эффективная площадь проходного сечения выхлопной линии.
Этой величиной необходимо предварительно задаться, руководствуясь следующими соображениями.
С увеличением Ω , при сохранении исходных данных неизменными, величина fэ уменьшается, а с уменьшением, наоборот fэ увеличивается. Это объясняется падением противодавления в полости выхлопа, препятствующего движению поршня, по мере относительного увеличения проходного сечения выхлопного канала но сравнению с подводящим.
В литературе [4 с. 117], приведены в виде номограмм зависимости безразмерной эффективной площади проходного сечения подводящей линии Uyкак функции безразмерной площади поршня 1/χдля различных значений Ω.
Кривые Uy=f(1/x) охватывают область значений Ω от 0,01 до бесконечности, причем Ω =∞ характеризуют предельный случай движения поршня с бесконечно большим выхлопным каналом, т.е. когда давление в полости выхлопа равно атмосферному в течение всего хода.
Для всех кривых характерно наличие минимума в области значений параметра 1/χ=1,35÷2,2Каждое значение Uy = Uyminопределяет минимальное сечение канала подводящей линии при данном Ω. При Ω = ∞ , Uymin=5,5и
1/χ=2.2.При относительно малых колебаниях значений силы сопротивления Р в качестве допустимого предела при проектном расчете можно принять [4]. χдоп=0.7 или 1/χ=1.43. В остальных случаях рекомендуется принимать
χ =0,4÷0,5 или 1/χ =2÷2,5.
Требуется выбрать параметры пневмопривода по следующим исходным данным:
Масса подвижных частей m=136кг;
Средняя скорость поршня Vср=1,02м/с;
Ход поршня L=0.8 м;
Полная сила сопротивления Р= 314,218Н;
Давление сжатого воздухаРм=0,8 МПа.
Возможность получения при заданных условиях установившегося движения поршня, показана ранее.
Определяем параметры привода из условия получения минимального проходного сечения подводящей .пинии fэ. В соответствии с рекомендациями при
Ω=∞, Uу=Uymin=5,5 и 1/χ=2,2.
По формуле (1.11) находим коэффициент пропорциональности:
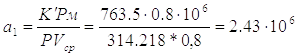 ,
, 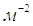
По формуле (1.14) находим коэффициент пропорциональности:
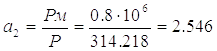 ,
, 
По формуле (1.10) находим эффективное минимальное проходное сечение:
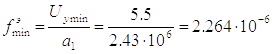 , м2
, м2
По формуле (1.13) находим оптимальную площадь поршня:
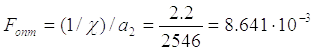 , м2
, м2
что соответствует диаметру цилиндра
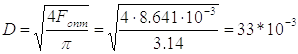 , м
, м
Округляем значение D до ближайшего большего из ряда стандартных размеров по СТ СЭВ 3936-82. В этом ряду имеются следующие значения D в мм: 10,12,16,20, 25,32, 40, 50,63, 80, 100,125, 160, 200, 250, 320,400, 500.
Принимаем D=40мм.
Диаметр штока выбирается в соответствии с рекомендациями [5].
Dшт=(0.2÷0.3)D
Диаметр Dшт, полученный из этого соотношения округляют до ближайшего значения стандартного рада по СТ СЭВ 3936-82. В нашем случае Dшт=0,25*40=10 мм. Принимаем Dшт =10 мм
1.3. Выбор параметров элементов пневмолиний
Размеры элементов пневмолиний, т.е. площади их проходных сечений f выбирают по принятой схеме соединения элементов друг с другом и с учетом соотношения f"э ≥ fэряс, где fэ- эффективная площадь проходногосечения линии, определенная в динамическом расчете пневмопривода.
Рассмотрим простейший частный случай, когда в линии входят только элементы одинакового проходного сечения, соединенные последовательно: f1= f2 =... fn. Решение данной задачи должно быть однозначным. Приведенная длина трубопроводов, эквивалентного всей линии всегда больше физической длины труб реальной системы. Вычислив по формуле (1.10) fэmin, выбравиз таблицы 1 типы пневмоаппаратов, определяют приведенную длину трубопровода Lэкв.
Таблица 1.1 - Основные характеристики пневмоэлементов.
|
Наименование аппарата |
Условный проход dy, мм |
Эффективная площадь fэ, мм2 |
Длина эквивалентного трубопровода Lэкв, м |
|
Фильтр В41-1 |
20 |
82 |
14,1 |
|
Маслораспределитель В63-1 |
20 |
118 |
17.6 |
|
Воздухораспределитель В63-2 |
20 |
87 |
7,5 |
Далее, по графику (рис. 2.2) для fэmin(ось ординат) и Lэкв, определяют коэффициент расхода µ и площадь проходного сечения пневмолиний по формуле:
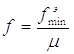 (1.15)
(1.15)
и диаметр пневмолиний dyпо формуле:
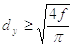
Найденное значение диаметра dy округляют до ближайшего большего по ГОСТ 11383-75.В соответствии с этим ГОСТ диаметры имеют следующие размеры: 6,8,10, 13, 15, 20, 25, 32 мм.
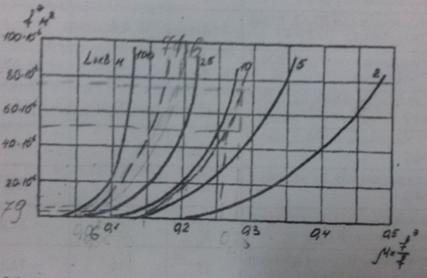
Рисунок 1.2 – График для приближенной оценки диапазона изменения
fэ/fпри проектном расчете пневматической линии
При динамическом расчете пневмопривода эффективная площадь подводящей магистрали fэmin =2,264*10-6м2. Длина пневмолинии L=14,5 м. Спроектированный пневмопривод состоит из фильтра типа В41-1 с dy=20мм, маслораспылителя типа В63-1 с dy=20мм и воздухораспределителя типа В63-2 с dy= 20мм. Определить проходное сечение пневмолинии и ее диаметр dy.
Определяем приведенную длину пневмолинии.
Lэкв=L+Lэфильтр+Lэмаслор+Lэраспр =
=14,5+14,1+7,5+17.6= 53,7м.
По графику (рис.1.2) для fэmin=2,264*10-6м2 и Lэкв=53,7 м,
определяем µ=0,075 ÷0,1 .
Следовательно, по формуле (2.15)
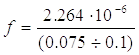 ;
;
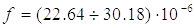 , м2
, м2
Что соответствует dy=(5,37÷6,201) мм.
Принимаем в соответствии с ГОСТ 11383-75 dy =6 мм, что соответствует
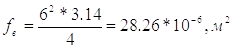
Определим коэффициент расхода µв выхлопной пневмолинии по изложенной выше методике.
Длину выхлопной пневмолинии до пневмораспределителя примем Lb=5 м. Так как воздух из штоковой полости (рис. 1.2) попадает в воздухораспределитель,
Lэраспр=7,5м.
Тогда Lэкв=5+7,5=12,5м.
По графику (рис.1.2) для fэmin=28,26*10-6м2 и Lэкв=12,5м,
определяем µ=0.18.
2.ДИНАМИЧЕСКИЙ АНАЛИЗПНЕВМОПРИВОД НАГРУЖЕННОГО ПОСТОЯННЫМИ СИЛАМИ
2.1. Анализ циклограммы типового пневмопривода
Типовой пневмопривод двухстороннего действия и его циклограммы показан на рис. 1.1. После срабатывания пневмораспределителя 4 воздух из магистрали подается по трубопроводу в полость рабочего цилиндра 5. Движение сжатого воздуха начинается тотчас же после момента начала открывания отверстия в распределителе. Некоторый период времени оба процесса (открывание отверстия распределителя и распространение волны давления сжатого воздуха до рабочего цилиндра) происходят одновременно и заканчиваются в разные моменты времени. Для упрощения задачи предположим, что волна давления возникает после полного открытия отверстия распределителя. При таком допущении не вносится большая погрешность, так как время открытия распределителя у большинства пневмоприводов невелико по сравнению с временем всего рабочего цикла. Вместе с тем указанное допущение позволяет отдельно определять интервалы времени этих процессов:
to- время открытия распределителя и tq - время распространения волны давления от распределителя до цилиндра.
Давление в рабочей полости пневмоцилиндра начинает увеличиваться после открытия пневмораспределителя и этот процесс продолжается до начала движения поршня. Назовем это время временем заполнения рабочей полости и обозначим tq. В этот же период времени давление во второй (штоковой) полости уменьшается. Сумму перечисленных временных интервалов, назовем временем подготовительного периода tп.
По определению
tn=to+tq+tз, (2.1)
В период движения поршня (интервал времени по циклограмме t,) давление может монотонно увеличиваться или колебаться в зависимости от соотношения конструктивных параметров устройства. После того, как поршень закончит рабочий ход L, давление в полости, соединенной с магистралью, увеличивается до значения, требуемого технологическим процессом. Во второй полости давление уменьшается до атмосферного. Моменты окончания этих процессов в общем случае несовпадают. После выполнения заданной технологической операции управляющее устройство (пневмораспределитель) снова переключается. Тогда в той же последовательности начинается обратный ход поршня в течение времени tз. Функции полостей пневмоцилиндра меняются.
Рабочей полостью назовем полость, соединенную в данный момент с магистралью, причем в этой полости давление сжатого воздуха является движущей силой.
Выхлопной полостью назовем полость, соединенную с атмосферной, причем давление воздуха в этой полости оказывает противодействие перемещению поршня.
Одна и та же полость привода в различные моменты времени может быть то рабочей, то выхлопной, например, при прямом и обратном ходах.
Рабочим циклом привода назовем такой период его работы, после которого все элементы привода возвращаются в исходное положение. Время рабочего цикла Tр.ц. привода состоит из суммы интервалов времени прямого t1и обратного tзходов.
Каждый из этих интервалов разделяется на следующие три интервала:
tп– время подготовительного периода от начала переключения распределителя до начала движения поршня;
t1- время движения поршня, в течение которого поршень пройдет весь заданный рабочий ход L.
Назовем временем срабатывания привода время перемещения поршня только в одном направлении.
В тех случаях, когда привод состоит из нескольких исполнительных устройств, его циклограмму строят в заданной последовательности их действия, а время работы привода находят после определения времени рабочего цикла каждого исполнительного устройства в отдельности.
2.2. Подготовительный период работы пневмопривода
Динамический расчет привода заключается в определении времени его рабочего цикла, т.е. в последовательном нахождении отдельных интервалов времени циклограммы. Время срабатывания пневмораспределителя определяют в зависимости от его конструкции. В большинстве случаев временем срабатывания распределителя в обычных условиях можно пренебречь как величиной незначительной по сравнению со временем рабочего цикла Тогда формула (16) примет вид:
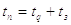 (2.2)
(2.2)
Время распространения волны давления от распределителя до рабочего пневмоцилиндра определяем по известной формуле.
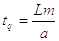 (2.3)
(2.3)
где L, - длина трубопровода от распределителя до цилиндра,
а - скорость распространения звука в воздухе, которая при Т=290 К равна 341 м/с.
При наполнении сжатым воздухом начального объема рабочей полости примем его давление на входе постоянным и равным магистральному, а потери давления на трение при течении воздуха по пневмолинии учтем посредством коэффициента расхода µ.
Такое допущение позволяет заменить процесс течения воздуха по трубопроводу процессом наполнения сжатым воздухом постоянного объема, эквивалентному объему трубопровода, а погрешности, получающиеся при этом, учесть коэффициентом расхода [4].
Подготовительный период охватывает интервал времени, когда в рабочей полости давление возрастает, а в выхлопной уменьшается, причем эти процессы протекают до тех пор, пока в обеих полостях установится перепад давлений, при котором движущая сила преодолеет силы сопротивления и поршень сдвинется с места. Следовательно, нужно определить время наполнения рабочей полости и время истечения сжатого воздуха из выхлопной полости до установления требуемого перепада давления.
За расчетное значение t, принимаем наибольшее из полученных.
Время наполнения сжатым воздухом рабочей полости определяется по уравнению [4].
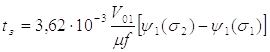 (2.4)
(2.4)
где: V01 - начальный объем рабочей полости и трубопровода, соединяющего ее с распределителем в м3;
µ - коэффициент расхода пневмолинии;
f - площадь поперечного сечения пневмолинии в м2;
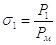 и
и 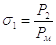 – начальное и
конечное давление в рабочей полости.
– начальное и
конечное давление в рабочей полости.
В начале процесса давление в рабочей полости атмосферное, т.е.:
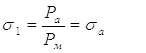
Время истечения сжатого воздуха из выхлопной полости определяется по уравнению:
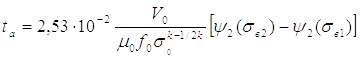 (2.5)
(2.5)
где: V0 - объем выхлопной полости в момент начала движения поршня.
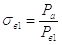 ;
;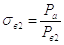 - начальное и конечное
давление в выхлопной полости.
- начальное и конечное
давление в выхлопной полости.
В уравнении (2.5) всем параметрам присвоен индекс «в» – выхлопная полость.
Значения функций 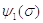 и
и 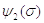 находим на графике, приведенном
на рис. 2.1.
находим на графике, приведенном
на рис. 2.1.
Давление в начале процесса истечения в выхлопной полости обычно равно магистральному, т.е.
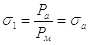










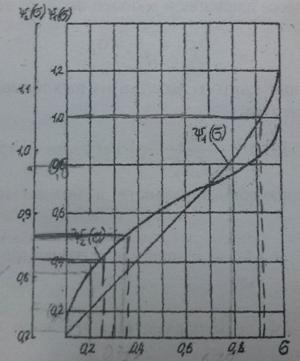
Рисунок 2.1– График для
определения функций 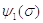 и
и 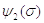 .
.
Чтобы произвести расчет по формулам (2.4) и (2.5), необходимо предварительно найти давление
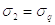 и
и 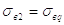
в обеих полостях пневмоцилиндра в момент начала движения поршня.
С этой целью следует воспользоваться номограммой (рис. 2.2) [4]. Посредством этой номограммы ; могут быть легко найдены давления в обеих полостях пневмоцилиндра в момент начала движения поршня. Так как номограмма построена в безразмерной форме, то предварительно должна быть определена нагрузка χ которая представляет собой отношение результирующей сил действующих на поршень к максимально возможной силе развиваемой приводом РмF т.е.
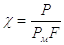 (2.6)
(2.6)
где F - площадь поршня.
Затем определяем величину
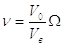 (2.7)
(2.7)
Где
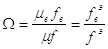 (2.8)
(2.8)


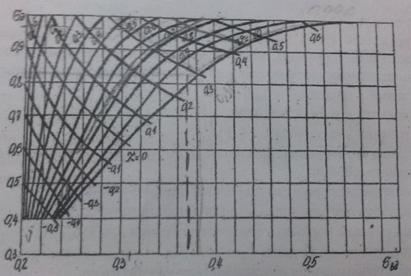
Рисунок 2.2 – Номограмма распределения безразмерных давлений в зависимости от безразмерной нагрузки
Номограмма (рис. 2.2) построена для значений σв=0,2 (Pм=0,5МПа)
и безразмерной площади пневмоцилиндра
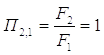
где F1, F2 площади поршня обоих его торцов.
При других значениях этих величин, например, наличие штока, следует вносить поправочные коэффициенты.
Величины практически мало зависят от Pмипри давлениях 0,3÷1 МПа может определяться по указанной номограмме (рис. 3.2). Величину находим пересчетом значения, взятого из графика, на новое значение давления Рм по приближенной формуле:
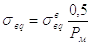 (2.9)
(2.9)
где Рм - необходимо брать в МПа.
При отклонении от единицы, в значения безразмерных давлений вносятся следующие поправочные коэффициенты:
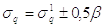 (2.10)
(2.10)
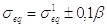
где 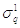 и
и 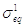 - давление при П2,1=1;
- давление при П2,1=1;
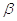 - отклонение П2,1 от единицы.
- отклонение П2,1 от единицы.
Знак поправочного коэффициента совпадает со знаком отклонения.
Определить время подготовительного периода двухстороннего типового пневмопривода, используя в качестве исходных данных результат динамического синтеза. В соответствии с этим расчетом, имеем:
диаметр поршня D=0.04 м;
диаметр штока Dшт=0,01м;
рабочий ход поршня L=0.8м;
длина трубопровода от цилиндра до распределителя Lт=5м, диаметр 0,006м;
коэффициент расхода подающей линии µ=0,075, а выхлопной µв=0,18;
нагрузка на поршень с учетом сил трения Р=314,218 Н;
давление в магистрали Рм=0.8 МПа.
Время срабатывания распределителя не учитывать.
Определяем время распространения волны давления tq:
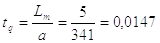 c
c
Находим начальные объемы рабочей и выхлопной полостей.
Рабочей полости:
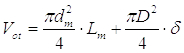
где δ принимаем равным 0,01 м, расстояние торца поршня до крышки пневмоцилиндра. Это расстояние принимается конструктивно,
из соображений, что 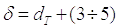 мм.
мм.
Тогда:
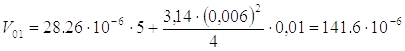 , м3
, м3
Выхлопной полости:
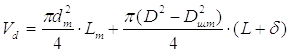
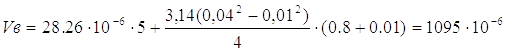 , м3
, м3
Определяем безразмерную нагрузку на поршень по формуле:
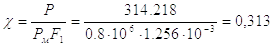 ,
,
Где
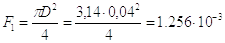 , м2
, м2
Находим значения относительных давлений σq и σвq в момент начала движения поршня, для чего предварительно вычисляем параметр:
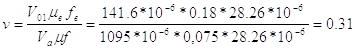
коэффициент:
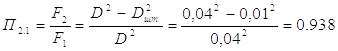
По номограмме на рис. 2.2 для χ=0,313 и v=0.31 находим
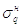 =1,03и
=1,03и 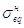 =0,283
=0,283
Учитывая, что П2,1=0,938 вносим соответствующие поправки:
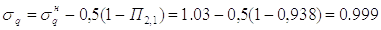
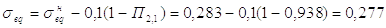
Определяем время наполнения рабочей полости до начала движения поршня по формуле:

где
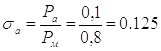
Значения функций 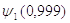 и
и 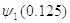 находим по графику
(рис. 2.1)
находим по графику
(рис. 2.1)
Они, соответственно, равны
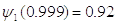 и
и 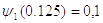
Тогда
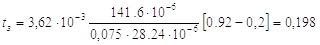 , с
, с
Время опоражнивания выхлопной полости определим по формуле:
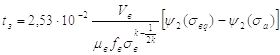
Значения функций 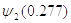 и
и 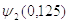 находим по номограмме (рис. 2.1).
Они, соответственно, равны :
находим по номограмме (рис. 2.1).
Они, соответственно, равны :
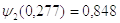 ,
,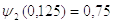 ;
;
Тогда
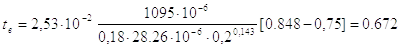 ,с.
,с.
Сравнивая время наполнения и опоражнивания полостей рабочего цилиндра, выбираем большее значение, т.е. tв=0.672 с.
В данном случае большая разница во времени объясняется главным образом малым значением нагрузки χ=0.313, благодаря чему давление в выхлопной полости изменилось значительно меньше, чем в рабочей полости.
Время подготовительного периода tп, равно:
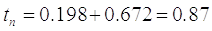 , с
, с
2.3. Период движения поршня
Так как в общем случае в пневмоприводе может быть несколько полостей, то в дальнейшем полости будем нумеровать, индексы параметров будут соответствовать нумерации полостей. На рис. 3.3первая полость является рабочей, а вторая – выхлопной.
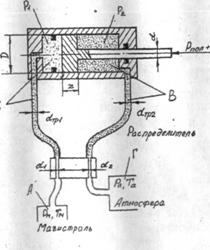
Рисунок 2.3– Период движения поршня
Уравнение движения поршня двухстороннего типового пневмопривода (рис.2.3)имеет следующий вид:
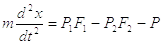 (2.11)
(2.11)
Где
m– масса привода и присоединенных к нему поступательно движущихся частей;
х – координата перемещения поршня;
P1, P2– давление воздуха в первой и второй полостях (полости Б и В).
Р – сила сопротивления на штоке. FbF2 - площади торцев поршня.
Дифференциальное уравнение (2.11) должно быть решено совместно с уравнениями характеризующими изменения давления в обоих полостях рабочего цилиндра.Эти уравнения получены без учета теплообмена с окружающей средой и при постоянных параметрах сжатого воздуха в магистрали.
Уравнение для определения давления Р1 в рабочей полости [4] имеет
вид:
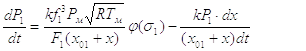 (2.12)
(2.12)
Где
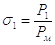 ;
;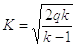 ;
;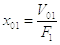 ;
;
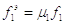 – эффективная площадь
входного отверстия;
– эффективная площадь
входного отверстия;
µ1– коэффициент расхода подводящей линии;
f1– площадь входного отверстия,
х01– приведенная начальная координата положения поршня;
V01– начальный объем рабочей полости.
В уравнении (2.11) значения функции расхода  равны:
равны:
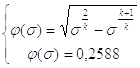 при
при 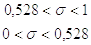 (2.13)
(2.13)
При определении начальной координаты положения поршня необходимо учитывать не только начальный объем полости (вредное пространство), но и объем трубопровода от распределителя до рабочего цилиндра
Уравнение для определения давления P2 в выхлопной полости [4] имеет вид:
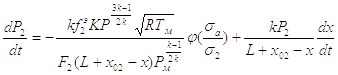 (2,14)
(2,14)
Значения функции расхода
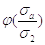
в уравнении (2.13) так же, как и в уравнении (2.12)равны
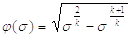 .
.
Совместное решение системы уравнений (2.11), (2.12), (2.13) возможно только с помощью численных методов интегрирования.
Шаг интегрирования выбирается в зависимости от требуемой точности расчета Интегрирование продолжается до тех пор, пока, значение перемещения X поршня не станет равным рабочему ходу L. Время, соответствующее этому моменту, равно времени перемещения поршня.
Приведенную систему дифференциальных нелинейных уравнений 4-го порядка (3.11, 3.12, 3.13) целесообразно[4] выразить в безразмерной форме, что дает возможность использовать одно решение для целой группы однотипных пневмоприводов. С учетом этого, введем следующие безразмерные переменные параметры:
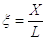 ;
; 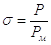 ;
; 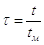
где
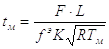 (2.15)
(2.15)
и безразмерные параметры:
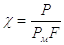
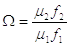
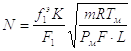 (2.16)
(2.16)
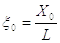
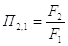 (2.17)
(2.17)
где N - постоянная величина характеризующая соотношение размеров и параметров данного привода;
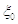 -
начальный объем полости;
-
начальный объем полости;
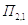 -
отношение площадей торцов поршня.
-
отношение площадей торцов поршня.
Выразив действительные перемещения, через безразмерные и подставив полученные значения в уравнения (2.11), (2.12), (2.13) получим следующую систему безразмерных уравнений:
уравнение движения
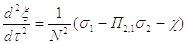 (2.18)
(2.18)
уравнение давления в рабочей полости
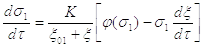 (2.19)
(2.19)
уравнение давления в выхлопной полости
 (2.20)
(2.20)
Систему нелинейных дифференциальных уравнений обычно решают одним из численных методов (Рунге-Купа, Адамса, Эйлера и др.).
Переход от безразмерных параметров к действительным осуществляется по формуле перехода:
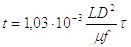 (2.21)
(2.21)
Указанная система уравнений (2.17, 2.18, 2.19) решена в институте машиноведения на ЭВМ для различных параметров пневматических приводов [4]. В результате для разных N, Ω и χ получены значения σ, ξ и соответствующие им интервалы времени. На основании этих расчетов построены сводные графики (рис. 2.4, 2.5), с помощью которых можно рассчитать время движения поршня пневмопривода. В приведенных ниже сводных графиках в интервал времени t включается не только время перемещения поршня, но и время t„ подготовительного периода.
Существует [4] следующий порядок расчета с помощью приведенных графиков. Сначала исходные физические параметры выражают в безразмерной форме. Затем по полученным безразмерным параметрам Ω, N и χ находят соответствующий график, по котором и определяют безразмерное время срабатывания τ и затем - действительное время t.
Изложим последовательность расчета:
Определяют безразмерную нагрузку/, по формуле:
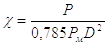 (2.22)
(2.22)
Определяют безразмерный конструктивный параметр N по формуле:
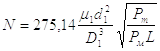 (2.23)
(2.23)
где Рm - вес груза и всех поступательно движущихся частей.
Определяют безразмерный коэффициент Q, характеризующий пропускные способности подводящей и выхлопной линий привода по формуле:
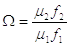 (2.24)
(2.24)
По полученному параметру Ω выбирают расчетный график. Если нет графика для данного значения Ω, то по двум ближайшим по значению Ω графикам производят интерполяцию.
Определяют приведенные начальные координаты положения поршня. Сначала вычисляют начальные объемы рабочей и выхлопной полостей с учетом объемов трубопроводов на участках труб от цилиндра до распределителя
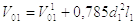 (2.25)
(2.25)
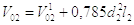
Затем определяют начальные координаты положения поршня:
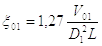 ;
;
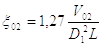 (2.26)
(2.26)
По этим параметрам так же проверяют расчетный график.
Выбирают график по значениям Ω, ξ01, ξ02, σa..
Определяют безразмерное время τпо выбранному графику по полученным значениям N и χ.
Определяют действительное время по формуле перехода:
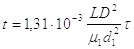 (2.27)
(2.27)
Определить время прямого хода поршня двухстороннего пневмопривода, используя в качестве исходных данных результаты динамического синтеза, рассмотренные ранее.
D=0,04 м;
L=0.8 м;
l1=12=5 м;
d1=d2=0,006м.
µ1=0,075м,
µ2=0,18м;
Р=314,218Н;
Рм=0,8 МПа,
Рm=100Н.
Определяем безразмерную нагрузку по формуле (2.21)
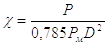 =0.313
=0.313
Определяем безразмерный конструктивный параметр N по формуле (2.22)
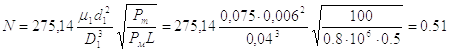
Определяем безразмерный коэффициенте по формуле (2.23)
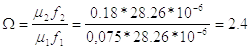
Определяем начальные объемы рабочей и выхлопной полостей по формуле (2.24). Ранее эти значения были определены при расчете времени подготовительного периода.
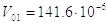 , м3
, м3
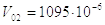 , м3
, м3
Начальные координаты положения поршня по формуле (2.25), равны:
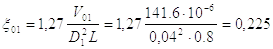 ,
,
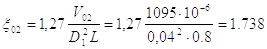 .
.
По графику для Ω=2;


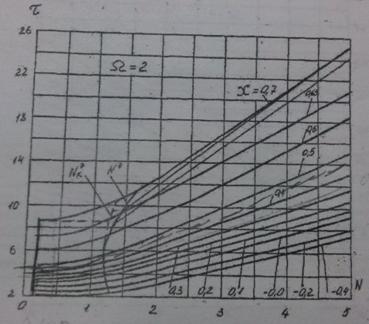
Рисунок 2.4 - График для Ω=2
σа=(0.2) при N=0,51 и χ=0,313 находим τ=3,9 с.
По графику для Ω=5;


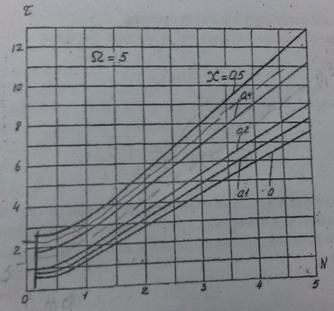
Рисунок 2.5 - График для Ω=5
σа=(0.5) при N=0,51 χ=0,313 находим τ=1,8 с.
Интерполируя, получим для Ω=2,4 τ=3,2
Определяем действительное время движения поршня по формуле(2.26)
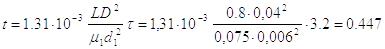 , c.
, c.
Так как время tвключает в себя подготовительное время tп, то время движения поршня
t’=t-tп=0,87 -0.447=0,423 c.
ЗАКЛЮЧЕНИЕ
Пневмоустройства используют в качестве приводов зажимных и транспортирующих механизмов, для дистанционного управления и регулирования, в контрольно-измерительных приборах, при автоматизации машин и устройств, работающих в агрессивных средах, в условиях пожаро- и взрывоопасности, радиации, а также при значительной вибрации и высоких температурах.
Широкое применение пневмоприводов объясняется их преимуществами по сравнению с другими, в первую очередь надежностью функционирования, простотой конструкции, сравнительной легкостью их эксплуатации и обслуживания. Они относительно дешевы и являются средством автоматизации производственных процессов.
Пневмоприводы следует применять в тех случаях, когда требуется обеспечить высокие скорости движения рабочего органа при относительно небольших рабочих усилиях. Основными типами исполнительных пневмоустройств, устанавливаемых в машинах, станках и автоматических линиях, являются пневмоцилиндры общепромышленного назначения. С их помощью достигаются относительно высокие скорости (1-3 м/с), что имеет большое значение для повышения производительности машин-автоматов, автоматических линий при выполнении вспомогательных операций (транспортировка, зажим, подача и т.д.). Диаметр пневмоприводов колеблется от 0,01 до 0,3 м, ход поршня от нескольких миллиметров до 2-3 м при самых разнообразных конструктивных исполнениях.
Срок службы пневмоцилиндров доведен до 10 млн. ходов. Давление питания в исполнительных пневмоустройствах обычно равно давлению сжатого воздуха в заводской сети (0,4-1МПа).
В процессе выполнения курсовой работы был рассчитан типовой двусторонний пневмопривод.
Определены начальные объемы рабочей (141.6 , м3) и выхлопной
( 1095, м3) полостей, определено действительное время движения поршня
t’=0,423,c.
СПИСОК ЛИТЕРАТУРЫ
1. Сборник задач по машиностроительной гидравлике под редакцией Куколевского И.И. М: Машиностроение, 1981
2. Вильнер Я.М. и др. Справочное пособие по гидравлике, гидромашинам и гидроприводам. Минск,:Вышэйшая школа, 1976
3. Башта Т.М. и др.. Гидравлика, гидромашины и гидропривода М.: Машиностроение, 1982
4. Герц Е.В., Крейнин Г.В. Расчет пневмоприводов. М.: Машиностроение, 1975.
5. Сункуев Б. С. Расчет, пневмо- и гидропривода машин легкой промышленности. Учебное пособие. Минск :БТИ им. С.М.Кирова, 1988.
6. Орлова Е.П. Методическое указание к выполнению курсовой работы «Пневматические устройства и системы» для студентов специальности 1-36 20 04 «Вакуумная и компрессорная техника». Минск,: БНТУ, 2011.
7.Методические указания по оформлению дипломных проектов для специальности 1-36 20 04 «Вакуумная и компрессорная техника» и направление специальности 1-08 01 01-01 «Профессиональное обучение (машиностроение)». – Минск: БНТУ, 2010













 (zip - application/zip)
(zip - application/zip)










