НИЖЕГОРОДСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
им Р.Е. Алексеева
Кафедра материаловедения и новых материалов
РЕФЕРАТ
ТЕМА: Тепловые свойства твёрдых кристаллических тел
Выполнил: студент гр.
09-ММ Гаврин В. С.
Проверил: Бетина Т. А.
Нижний Новгород, 2012 г.
Содержание
 |
1. Колебания трехмерной кристаллической решетки ______________
2. Фононы __________________________________________________
3. Теплоемкость кристаллической решетки. ________________________
4. Дебаевская теория теплоемкости кристаллов:__________________
5. Тепловое расширение твердых тел______________________________
6.Теплопроводность кристаллической решетки__________________
Использованная литература ____________________________________
1. Колебания трехмерной кристаллической решетки
Тепловое движение атомов (ионов, ядер) кристаллической решетки является колебательным. Вследствие взаимодействия атомов такой колебательный процесс приводит к распространению по кристаллу волн. Нагрев или охлаждение образца проявляется в увеличении или уменьшении энергии колебаний, а также в ее перераспределении между различными типами волн.
Произвольное колебательное движение может быть представлено в виде суперпозиции бегущих в различных направлениях плоских монохроматических волн. Волны отличаются друг от друга длиной волны, амплитудой, поляризацией и законом дисперсии. Во избежание ошибки заметим, что бегущая волна не есть движение атомов, расположенных вдоль какой-нибудь прямой. Это коллективное движение всех без исключения частиц, составляющих решетку.
Важнейшая характеристика плоской монохроматической волны — волновой вектор q. Он задает длину волны λ=2π/q и направление распространения. Все физически различные значения q лежат в первой зоне Бриллюэна, построенной для обратной решетки в пространстве волновых чисел.
< Первая зона Бриллюэна (часто называемая просто зоной Бриллюэна) может быть построена как объём, ограниченный плоскостями, которые отстоят на равные расстояния от рассматриваемого узла обратной решётки до соседних узлов: >

Рис. 1. Первая зона Бриллюэна для простой кубической (а)
и гексагональной (б)решёток
Учет условий периодичности по большому периоду приводит к квантованию волнового вектора. Имеется N(N =N1N2N3 — число ячеек в блоке с размерами N1al, N2a2 и N3a3 по направлениям векторов основных трансляций) различных по величине и направлению векторов q.
2. Фононы
В части перехода к нормальным координатам квантовая механика не расходится с классической. И в квантовой теории переход к переменным нормальным координатам позволяет представить решетку как совокупность гармонических осцилляторов. Квантовое состояние решетки задается набором 3Np квантовых чисел νqB. Ее энергия, если отбросить энергию нулевых колебаний всех осцилляторов, равна
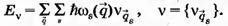 Точно такое же выражение для энергии мы получим, если рассмотрим идеальный газ, состоящий из частиц, характеризующихся волновым вектором q, энергией
Точно такое же выражение для энергии мы получим, если рассмотрим идеальный газ, состоящий из частиц, характеризующихся волновым вектором q, энергией 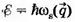 и законом дисперсии ωs(q). При этом числа V- задают количество частиц, находящихся в квантовом состоянии (q; s). В данном случае физический смысл квантовой характеристики q заключается в том, что эта величина определяет квазиимпульс р, который равен hq.
и законом дисперсии ωs(q). При этом числа V- задают количество частиц, находящихся в квантовом состоянии (q; s). В данном случае физический смысл квантовой характеристики q заключается в том, что эта величина определяет квазиимпульс р, который равен hq.
Представление о таком идеальном газе очень удобно: с его помощью можно наиболее просто и наглядно выразить то обстоятельство, что энергия решетки изменяется не произвольно, а только порциями, по величине равными hωs(q). Частицы этого газа получили название фононов.
Таким образом, в квантовой теории существуют два эквивалентных подхода, два языка, одинаково хорошо описывающих движение атомов решетки.
● С одной стороны, мы имеем набор гармонических осцилляторов, частоты которых суть частоты нормальных колебаний решетки. Осцилляторы нумеруются значениями вектора q и квантового числа s. Осциллятор, возбужденный до квантового состояния vq, описывает коллективное движение с определенной энергией 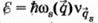 - и квазиимпульсом р.
- и квазиимпульсом р.
● С другой стороны, это же квантовое число vq трактетуется как число фононов, имеющих энергию 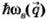 и квазиимпульс hq.
и квазиимпульс hq.
Число фоноррв в каждом из возможных квантовых состояний может быть любым. Это означает, что фононы являются бозонами. Им приписывается нулевой спин. Прямая аналогия с фотонным газом позволяет записать функцию статистического распределения фононов По квантовым состояниям в условиях термодинамического равновесия как для бозе-газа:
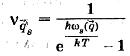
Здесь vq — среднее число частиц, приходящихся на одно квантовое состояние.
Представление о фононном газе очень удобно и полезно при изучении внешних воздействий на решетку, при расчетах взаимодействий электронов с колебаниями решетки и при исследовании многих других сложных процессов, которые таким образом сводятся к элементарным актам столкновений фононов с другими частицами или друг с другом.
При столкновениях выполняются законы сохранения энергии (ξ) и квазиимпульса (р), но число фононов может изменяться. Поэтому столкновение электрона и фонона может привести к появлению фонона нового сорта или просто к исчезновению прежнего. Этим процессам отвечают равенства, вытекающие из законов сохранения:
Число возможных каналов реакции с фононами расширяется за счет процессов переброса. Так называются столкновения, в которых фонон получает квазиимпульс (или волновой вектор), выходящий за пределы первой зоны Бриллюэна. Все значения квазиимпульса могут быть «приведены» в зону Бриллюэна путем вычитания некоторого вектора обратной решетки. Поэтому формально получается реакция с нарушением закона сохранения квазиимпульса.
Для изучения акустических колебаний решетки или, что то же самое, фононов с малым волновым числом исследуются звуковые волны в кристалле. Поглощение света нагревает образец. Оно особенно интенсивно, когда частота света ω удовлетворяет условию Бора
где h*ω=∆E — разность соседних колебательных уровней. На фононном языке здесь имеет место превращение фотона в фонон той же энергии (частоты) и с тем же импульсом.
Наиболее богатую информацию о колебаниях решетки дает неупругое рассеяние нейтронов на кристалле. Пролетая через образец, нейтрон взаимодействует с ядрами и, передавая им часть энергии, «раскачивает» колебания. Это означает, что нейтрон порождает фононы. В одном акте взаимодействия изменение импульса и энергии нейтрона равно:
Отсюда видно, что неупругое рассеяние нейтронов позволяет непосредственно изучать закон дисперсии квазиимпульса у фононов.
Фонон есть представитель особого мира физических объектов, так называемых квазичастиц. Практически всякому виду коллективного движения в кристалле можно сопоставить определенный сорт квазичастиц. Для этого необходимо выделить подсистему, в которой проявляется данный вид движения, и ввести нормальные координаты, в которых обособляются друг от друга различные степени свободы подсистемы. Дальше вводится в действие стандартный математический аппарат, родственный тому, который используется в квантовой теории поля.
3. Теплоемкость кристаллической решетки
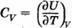 Изохорическая теплоемкость определяется как производная от внутренней энергии U по температуре : [1]
Изохорическая теплоемкость определяется как производная от внутренней энергии U по температуре : [1]
Внутренняя энергия в классической статистике рассчитывается следующим образом. Тело, состоящее из N атомов, имеет 3N колебательных степеней свободы, причем средняя энергия, приходящаяся на одну колебательную степень свободы, равна кТ. Тогда внутренняя энергия тела есть U=3NkT. [2]
Из выражения (1) и (2) следует Закон Дюлонга и Пти: Сv=ЗNk [3]
(k- постоянная Больцмана).
Выражение (3) оправдывается только для достаточно высоких температур, Гораздо лучшие результаты дает простейшая квантовая теория теплоемкости, разработанная А. Эйнштейном в 1905 г.
В ней предполагается, что все 3N атомных осцилляторов имеют одну и ту же частоту колебаний ω. Если учесть дискретность значений энергии квантового гармонического осциллятора, то для средней энергии осциллятора получаем формулу:
|
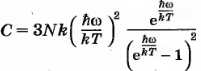
Если Т>>hω/k, то, заменяя экспоненту в числителе единицей, а в знаменателе оставляя два члена в разложении экспоненты, снова приходим к выражению (3). При Т→0 теплоемкость С стремится к нулю, как того требует третье начало термодинамики, однако количественного согласия с опытом при низких температурах эта формула не дает. Более совершенная теория, развитая в 1912 г. П. Дебаем, позволила объяснить экспериментальную зависимость С →Т3, характерную для интервала температур вблизи абсолютного нуля.
4. Дебаевская теория теплоемкости кристаллов
Дебай предполагал, что наибольший вклад в теплоемкость дают волны с большой длиной волны. При λ>> а (а - постоянная решетки) атомная структура кристалла практически не сказывается. Вещество уподобляется сплошной среде. В таком образце по заданному направлению могут распространяться две поперечных и одна продольная волна. Фазовые скорости различных типов волн, вообще говоря, различны. Будем считать, что для двух поперечных типов волн фазовые скорости одинаковы. Обозначим символами v┴ и v ║ фазовые скорости поперечных и продольных волн соответственно. Эти величины считаются постоянными, не зависящими от длины волны. Поэтому закон дисперсии оказывается очень простым: ω= v┴*q.или ω= v║*q.
Так как теплоемкость не зависит от размеров и формы тела, допустим, что образец есть куб с ребром L. Нормальным колебаниям среды сопоставляются стоячие волны различных частот и амплитуд колебаний, устанавливающиеся по всем возможным направлениям.
Необходимо подсчитать число стоячих волн dn(ω), частоты которых попадают в интервал (ω, ω + d ω).
Волны в однородной и изотропной среде описываются решениями волнового уравнения
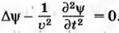
Граничным условием здесь является требование периодичности
 [4]
[4]
Ему удовлетворяет стоячая волна
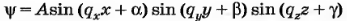 [5]
[5]
С волновым вектором:
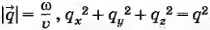 [6]
[6]
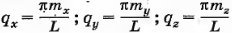 Проекции его удовлетворяют вытекающим из граничных условии 4 соотношениям:
Проекции его удовлетворяют вытекающим из граничных условии 4 соотношениям:
где mx, my, и mz — числа натурального ряда.
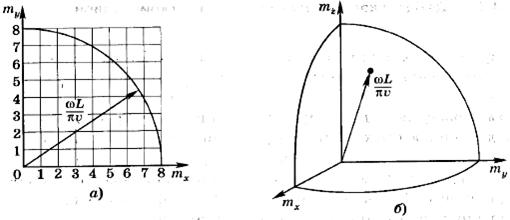
Рис. 2.
Каждой стоячей волне соответствует свой набор чисел тх причем из 5 с учетом 6 следует, что 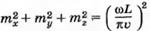 [7]
[7]
Используем последнее равенство для нахождения dn(co). Для этого перейдем в условное пространство, где по осям декартовых координат откладываются числа тх ту тz. Каждой стоячей волне в этом пространстве отвечает точка с целочисленными координатами тх, ту и тz, расположенная в первом октанте (рис. 2, б). Из рис. 2, а видно, что на каждую стоячую волну приходится единичный объем условного пространства. Поэтому в согласии с (7) число стоячих волн n(ω) с частотами от 0 до ω приблизительно равно одной восьмой объема сферы радиуса ωL/πν, т. е.
Дифференцируя это выражение по частоте, получаем, Что
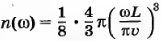
где V = L3 — объем данного образца.
Если учесть три различных поляризации волны, то искомое число стоячих волн увеличится. Получаем для числа стоячих волн, частоты которых попадают в интервал (ω, ω + dω), выражение dn(ω)=B ω 2d ω, [8]
Общее число стоячих волн в сплошной среде бесконечно, число же степеней свободы (3N) у реального кристалла велико, но ограниченно. Поэтому при расчете теплоемкости следует ограничить интервал возможных частот колебаний некоторым максимальным значением частоты ω0. Теперь можно вычислить энергию решетки:
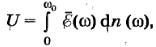
где ξ(ω) — средняя энергия колебаний осциллятора (приходящаяся на одну стоячую волну). Для исследования функции U(T) удобно перейти к новой переменной x=hω/kT и ввести характерный параметр — дебаевскую температуру θ=hω0/k
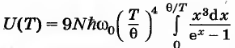 [9]
[9]
При Т >> θ переменная интегрирования х принимает значения, много меньшие единицы. В этом случае полагаем ех ≈ 1 + х
и расчет теплоемкости снова приводит, как и следовало ожидать, к классическому соотношению 3.
Если Т << θ, верхний предел интегрирования можно принять равным бесконечности. Тогда имеем U≈Т4, и С≈Т3, что совпадает с экспериментальными данными при Т→0.
Таким образом, теория Дебая верно описывает поведение теплоемкости кристалла в предельных случаях высоких и низких температур. В промежуточном интервале температур эта теория далеко не во всех случаях полностью согласуется с опытными данными (поэтому формулу теплоемкости по Дебаю называют интерполяционной.
Лучшие результаты теория Дебая дает для кристаллов с одним атомом в ячейке. Это указывает на то, что теория Дебая учитывает акустические и не учитывает оптические колебания решетки.
Точные результаты дает последовательная квантовая теория теплоемкости, в соответствии с которой энергия решетки рассчитывается как сумма энергий фононов.
5. Тепловое расширение твердых тел.
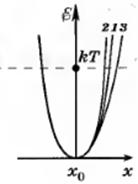
При нагревании тела энергия сообщается как ядрам, так и электронам. Если при этом квантовое состояние электронной подсистемы кристалла не изменяется, то можно говорить только об увеличении колебательной энергии, которая равна сумме кинетической энергии ядер и энергии электронов ξn(R), которая при движении ядер играет роль потенциальной энергии. Будем использовать для ξn(R) обозначение U(R) и полагаем, что в узлах решетки находятся целые атомы.
Максимальное значение U(R) равно полной энергии колебаний Е. Минимальное значение можно принять равным нулю (т. е. U(R0) = 0). Отсюда видно, что при нагревании изменяются расстояния между атомами, т. е. нагрев приводит к тепловому расширению образца. Для численной оценки эффекта найдем среднее расстояние между атомами в одномерной цепочке, изображенной на рис. 3: .
.
Положения атомов задаются их смещениями ξi относительно положения равновесия (узла решетки). Можно считать, что величины ξi изменяются беспорядочно, хаотически. Вероятность того, что эти параметры примут значения ξi задается каноническим распределением Гиббса. В нашем случае его можно записать в виде:
|
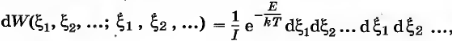
|
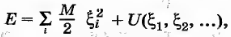
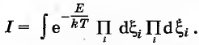
|

Это означает, что сила взаимодействия между соседними атомами не пропорциональна изменению расстояния между ними, а следует более сложному закону
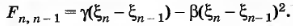
Именно второй, ангармонический член в формуле для силы ответствен за удлинение образца.
Воспользовавшись распределением (10) и произведя ряд преобразований, получим zn - среднее значение изменения расстояния между атомами:
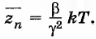
Зная средние значения расстояний между атомами zn в зависимости от температуры T можно рассчитать коэффициент теплового расширения, который определяется соотношением:
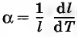
Где l — длина образца. Расстояние dn между п-м и (n - 1)-м атомами равно
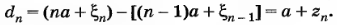 Учитывая, что
Учитывая, что

|
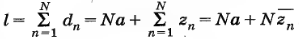
 Отсюда (при zn << a) имеем:
Отсюда (при zn << a) имеем: 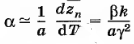
|
6. Теплопроводность кристаллической решетки
В общих чертах механизм теплопроводности кристаллической решетки давно известен, однако точный анализ явления оказывается настолько сложным, что и сейчас возможны только довольно грубые оценки.
Для исследования процесса переноса тепла в решетке с использованием волновых представлений следует учесть, что тепловое движение атомов в кристалле представляет собой беспорядочные колебания около положений равновесия. Поэтому для их описания необходимо ввести волновое поле, хаотически изменяющееся в каждой точке кристалла.
Поскольку температура определяет среднюю интенсивность (а также распределение энергии по частотам и другие характеристики) волнового процесса, то в случае, если тело нагрето неоднородно, плотность энергии волнового поля оказывается неодинаковой в различных частях образца.
Так как бегущая волна несет энергию, казалось бы, нетрудно на волновом языке описать передачу энергии от более нагретых участков к менее нагретым, но это не так просто. Дело в том, что в среде с дисперсией скорость течения энергии не совпадает со скоростью распространения волн. Сложности рассмотрения этим не ограничиваются. Следует вычислить вклад отдельных монохроматических составляющих, учесть интерференцию волн и их рассеяние на дефектах решетки, а также и возможное взаимное рассеяние волн, если колебания атомов являются ангармоническими.
Значительно проще описание механизма теплопроводности с использованием понятия о фононном газе (при этом подходе слова «атомы», «решетка» могут быть забыты). Кристалл следует рассматривать как объем, наполненный идеальным фононным газом.
Согласно распределению (0) у нагретой стенки будет больше фононов с высокими энергиями, чем у холодной. При одинаковой всюду концентрации фононов число этих квазичастиц, пересекающих в каждый момент выделенную плоскость слева направо и в обратном направлении, справа налево, одинаково. Вследствие разности температур по обе стороны плоской поверхности средние энергии фононов в этих потоках различны, и поэтому возникает поток энергии в сторону более холодного газа, от стенки с более высокой температурой к стенке с меньшей температурой.
Такой процесс возможен в любом газе. Поэтому нет необходимости заново вычислять коэффициент теплопроводности для фононного газа. Можно воспользоваться готовой формулой молекулярно-кинетической теории :
|
|
где с — теплоемкость единицы объема (в данном случае это теплоемкость на единицу объема решетки), u, l — средняя скорость хаотического теплового движения и средняя длина свободного пробега фононов соответственно.
Теплоемкость найдем из соотношения
|
|
где V — объем образца.
Чтобы найти среднюю скорость фононов u, требуется произвести двойное усреднение. Дело в том, что фонон, находящийся в квантовом состоянии с энергией ξ и квазиимпульсом р, не имеет определенной скорости движения. Для него можно указать лишь среднее значение этой величины. Можно показать, что квантовое среднее находится из соотношения
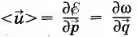
Далее модуль усредняется по распределению (0): z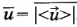
Как правило, в расчетах используется дебаевское приближение:
(ω= v┴*q.или ω= v║*q.): предполагается, что все фононы имеют одну и ту же скорость v, равную скорости звука в среде, т. е. u = v.
Наибольшие трудности связаны с расчетом длины свободного пробега. В молекулярно-кинетической теории для этой величины имеется выражение l=1/nS [12]
где n - концентрация мишеней, т. е. частиц, с которыми может столкнуться движущаяся молекула, S — поперечное сечение мишени.
Если решетка не имеет дефектов, то препятствовать движению фонона могут лишь другие фононы. Поэтому величину n в формуле (11) следует принимать равной концентрации фононного газа. Что касается S, то это будет некоторая эффективная величина, характеризующая взаимодействие фононов друг с другом.
Формула для концентрации фононов:
|
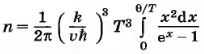
Фазовый объем, приходящийся на все состояния фонона, если он движется в пределах объема V и модуль его импульса изменяется в интервале от р до р + dp (все направления движения равновероятны), выражается формулой
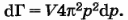 [13]
[13]
Где θ – дебаевская температура. θ=ξ0/k
Из анализа формулы (9.37), аналогичного анализу формулы (9.16), следует, что при Т >> θ, n ≈ T, а при Т << θ, n ≈ Т3.
Использованная литература:
1. А. С. Василевский. Физика твёрдого тела. Дрофа. 2010 г. 206 стр.
2. Павлов П.В., Хохлов А.Ф. Физика твердого тела. Учеб. - 3-е изд., М. ,
2000 г. - 494.
3. А. С. Давыдов Теория твёрдого тела. — М: Наука, 1976 г. — 640 с.















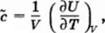
 (zip - application/zip)
(zip - application/zip)










