Связность, компактность. Непрерывные отображения. Гомеоморфизм, примеры. Прямая на плоскости

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования

«Вятский государственный университет»

(ФГБОУ ВПО «ВятГУ»)

Реферат

По алгебре и геометрии

На тему:

 «Связность, компактность. Непрерывные отображения. Гомеоморфизм, примеры. Прямая на плоскости.»

Выполнила студентка группы ИВТ-11 _____________ /Садакова Ю.В.

Проверила преподаватель ______________________/Серова А.С.

Киров 2012

Связность

Понятие связности есть математически строгое отражение интуитивного представления о целостности геометрической фигуры.

Определение Топологическое пространство Х называется несвязным,  если его можно представить в виде объединения двух непустых непересекающихся открытых (замкнутых) множеств

 ,

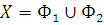в противном случае пространство называется связным.

Теорема1 Пусть в топологическом пространстве Х даны два непустых непересекающихся замкнутых множества 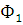 и 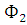,  непустое связное множество М, содержащееся в объединении множеств

тогда множество М содержится в каком-нибудь одном множестве

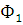  или .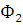

 

Доказательство:

Имеем 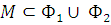  . Представим множество М в виде

.

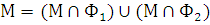Так как Ф₁  и Ф₂  замкнуты, то множества 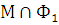 и 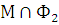 замкнуты в М. Так как множество М связно,  то одно из множеств 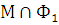или

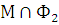 должно быть пустым, откуда и следует утверждение теоремы.

Что требовалось доказать.

Теорема2  Если для любых двух точек  х и у пространства  Х можно найти связное множество С_xy , содержащее эти точки, тогда все пространство Х связно.

Доказательство:

 Предположим, что все пространство Х несвязно т.е.

 ,

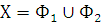где Ф₁  и Ф₂ непустые непересекающиеся множества. Возьмём

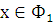, а y ∈ Ф₂. Тогда связное множество С_xy , имеющее с множеством Ф₁ общую точку х, должно содержаться в этом множестве. С другой стороны,  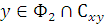 и, следовательно, множество С_xy должно содержаться во множестве Ф₂. Но множества Ф₁ и Ф₂ не пересекаются. Полученное противоречие и доказывает теорему.

Что требовалось доказать.

Компактность

         Определение Множество называется компактным, если каждая бесконечная последовательность его элементов (точек) имеет хотя бы одну предельную точку. 

         В математическом анализе большое значение имеет принцип Вейерштрасса, утверждающий, что каждое ограниченное множество действительных чисел — компактно. Компактные множества функций играют фундаментальную роль в теории функций и функциональном анализе. Для того чтобы множество Е непрерывных (например, на сегменте [0,1] числовой прямой) функций было компактно (в пространстве С всех непрерывных на [0,1] функций), необходимо и достаточно, чтобы функции множества Е были ограничены в своей совокупности (одной и той же постоянной) и равностепенно непрерывны

        Компактное  метрическое пространство называется компактом. Среди множеств, лежащих в евклидовых пространствах Eⁿ произвольного числа измерений, компактны в Eⁿ все ограниченные множества и только они; компактами (то есть компактными в себе множествами) среди них будут лишь замкнутые (и ограниченные) множества.

Непрерывные отображения

Пусть (Х,τ) и (Y,μ) - топологические пространства и отображение 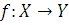 – отображения из Х в Y. 

Определение Отображение f называется непрерывным в точке , если для любой окрестности v точки 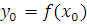 существует такая окрестность u точки 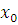, что 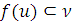. Отображения f называется непрерывным на множестве Х, если оно непрерывно в каждой точке .

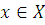Гомеоморфизм

Определение Взаимно однозначное и взаимно непрерывное отображение одного  топологического пространства в другое называется гомеоморфизмом.

Если существует гомеоморфное отображение одного пространства на другое, то пространства называются гомеоморфными.

Определение Два топологических пространства называются топологически  эквивалентными или имеющими один топологический тип, если существует  гомеоморфизм одного пространства на другое.

Примеры:

1. Любое отображение дискретного пространства в топологическое пространство непрерывно. Следовательно, два дискретных пространства гомеоморфны  тогда и только тогда, когда существует взаимно однозначное отображение одного пространства на другое. 

2. Числовая прямая гомеоморфна интервалу (0;1). Гомеоморфизм устанавливает функция   .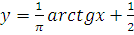

3. Сфера и поверхность куба в пространстве R³  гомеоморфны. (На сфере и кубе естественная топология индуцируется топологией пространства  R³ ).  Если совместить центры сферы и куба, то гомеоморфизмом будет отображение проектирования из общего центра.

Прямая на плоскости

Определение  Уравнением линии на плоскости 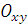 называется уравнение, которому удовлетворяют координаты x  и y  любой точки данной линии и не удовлетворяют координаты любой точки, не лежащей на этой линии.

Теорема Всякое уравнение первой степени 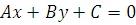, где A и B  не обращаются в нуль одновременно, представляет собой уравнение некоторой прямой линии на плоскости O_xy .

Основные уравнения прямой на плоскости:

1)  Ax+By+C=0 - общее уравнение прямой;

2)  A(x-x₀)+B(y-y₀)=0 - уравнение прямой, проходящей через точку 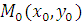 перпендикулярно вектору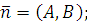 

3) 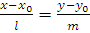      - каноническое уравнение прямой, проходящей через точку M₀(x₀ ,y₀) параллельно направляющему вектору 

4) 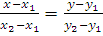      -   уравнение прямой, проходящей через две точки 

M₁(x₁,y₁) и M₂(x₂,y₂);

5)       - уравнение прямой в отрезках, где a и b  - некоторые отличные от нуля действительные числа.

6) 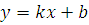      - уравнение прямой с угловым коэффициентом, где k – угловой коэффициент прямой, а b – отрезок, отсекаемый прямой на оси O_y

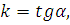( где 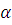 – угол между прямой и положительным направлением оси O_x);

7) 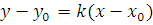      - уравнение прямой (или пучка прямых), проходящей через точку M₀(x₀,y₀), где k – угловой коэффициент прямой.

 

Список литературы

1.      Лекции по топологии [Текст] / В.Н. Худенко, В.В. Махоркин, И.А. Хрусталев, Ю.Н. Карамзин - Калининград: Изд-во КГУ, 2000. - 110 с.

2.     Высшая математика [Текст]: учебное пособие / Л.С. Никулина, А.А. Степанова - Владивосток: Изд-во ВГУЭС, 2000. – 55 c.