Свойства Преобразования Фурье

Реферат

на тему
«Свойства Преобразования Фурье»

Содержание:

1.     Линейность преобразования Фурье

2.     Характеристики Фазы

3.     Периодический Характер(природа) ДПФ

4.     Сжатие и Расширение(растягивание), методы Мультичастоты

5.     Умножение Сигналов (Амплитудная Модуляция)

6.     Преобразование Фурье(трансформанта Фурье) дискретное Время

7.     Отношение Парсевала

Домены времени и частоты - альтернативные пути представления сигналов. Преобразова-ние Фурье - математические отношения между этими двумя представлениями. Если сиг-нал изменяется в одном домене, это будет также изменено в другом домене, хотя обычно не таким же образом. Например, это показывалось в прошлой главе, что скручивание сиг-налов домена времени приводит к их умноженным частотным спектрам. Другие матема-тические операции, типа сложения, масштабирования и смещения, также имеют операцию соответствия в противоположном домене. Эти отношения называются свойствами преоб-разований Фурье, как математическое изменение в одном домене приводит к математиче-скому изменению в другом домене.

1.    Линейность преобразования Фурье

Преобразование Фурье линейно, то есть обладает свойствами однородности и аддитивности. Рисунок 10-1 обеспечивает пример того, как однородность является свойством преобразо-вания Фурье. Рисунок (a) показывает произвольный сигнал домена времени , с соответст-вующим спектром частот, показанным в (b). Мы назовем эти два сигнала: x[] и X[], соответственно.

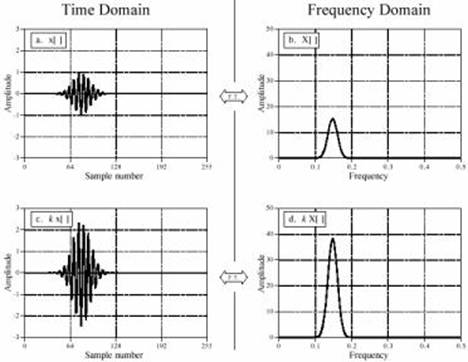
Рис. 10-1. Однородность(гомогенность) преобразования Фурье.

            Однородность означает, что изменение в амплитуде в одном домене производит идентичное изменение в амплитуде в другом домене.

В математической форме, если x[ ] и X[ ] - пара преобразований Фурье, то k x[ ] и k X[ ] - также пара преобразований Фурье, для любой константы k. Если частотный домен пред-ставлен в прямоугольной системе обозначений, k X[ ] означает, что и вещественная часть и мнимая(несобственная) часть умножена на k. Если частотный домен представлен в по-лярной системе обозначений , k X[ ]означает, что величина - умноженная k, в то время как фаза остается неизменяемой.

Аддитивность преобразования Фурье(трансформанты Фурье) означает, что сложение в одном домене соответствует сложению в другом домене. Пример этого показывается на рис. 10-2.

Рис. 10-2. Аддитивность преобразования Фурье.

В этой иллюстрации, (a) и (b) - сигналы в домене времени, называемые x₁[ ] и x₂[ ], соответственно. Сложение этих сигналов производит третий сигнал домена времени, называемый x₃[ ], показанный в (c). Каждый из этих трех сигналов имеет спектр частот, состоящий из реальной(вещественной) и мнимой(несобственной) части, показанный в рис. от (d) до (i). Так как два сигнала домена времени складываясь, производят третий сигнал домена времени, два соответствующих спектра складываясь, производят третий спектр. Частотные спектры сложены в прямоугольной системе обозначений, прибавляя вещест-венные части к вещественным частям и мнимые части к мнимым частям. Все волны косинуса складываются (вещественные части) и все волны синуса складываются (мнимые части) без взаимодействия между двумя(попарно).

Если: x₁[n] + x₂[n] = x₃[n], тогда: ReX₁[f ] + ReX₂[f ] = ReX₃[f ] и ImX₁ [f ] + ImX₂[f ] = ImX₃[f ].

2.    Характеристики Фазы

3.    Периодический Характер(природа) ДПФ

4.    Сжатие и Расширение(растягивание), методы Мультичастоты

Как показано в рис . 10-12, сжатие сигнала в одном домене приводит к расшире-нию(растягиванию) в другой, и наоборот. Для непрерывных сигналов, если X(f ) - преоб-разование Фурье(трансформанта Фурье) x( t), то 1/k x X(f/k) - Преобразование Фу-рье(трансформанта Фурье), x(kt) где, k - параметр, управляющий расширени-ем (разложением) или сжатием (сокращением ). Если событие случается быстрее (это сжато во времени), это должно быть составлено из более высоких частот . Если событие случает-ся медленнее (это расширено(растянуто) во времени), это должно быть составлено из бо-лее низких частот. Этот образец проводит если взято в любые из этих двух крайностей. То есть, если сигнал домена времени сжат пока, что это становится импульсом, соответст-вующий спектр частот расширен пока, что это становится постоянным значением. Анало-гично, если домен времени расширен(растянут), пока это не становится постоянным зна-чением, частотный домен становится импульсом.

Дискретные сигналы ведут себя подобным способом, но имеются еще несколько подроб-ностей. Первая проблема с дискретными сигналами - наложение спектров(псевдоним). Вообразите что домен время. Вообразите, что спектр частот в (f) сжат намного жестче, приводя к сигналу домена времени в (e), расширяющемся в соседние периоды.

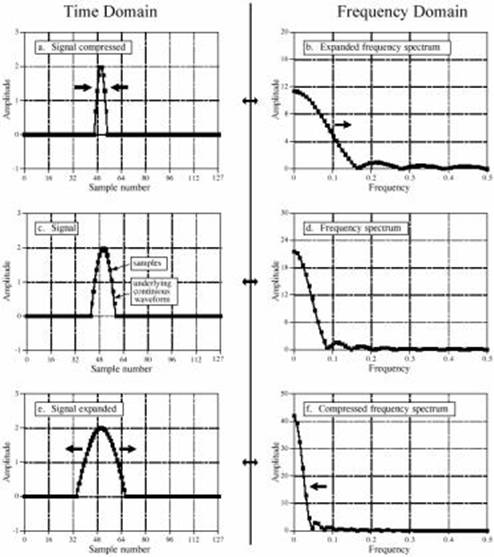
                Рис. 10-12. Сжатие и расширение(растяжение).

Вторая проблема должна определить точно, что это означает сжимать или разворачивать дискретный сигнал. Как показано в рис. 10-12a, дискретный сигнал сжат, сжимая основ-ную непрерывную кривую, что выборки лежат на, и затем перевыбирается новая непре-рывная кривая, чтобы найти новый дискретный сигнал. Аналогично, этому тот же самый процесс для разворачивания дискретных сигналов показывают в (e). Когда дискретный сигнал сжат, события в сигнале (типа ширины импульса) случаются излишне малым чис-лом выборок. Аналогично, события в расширенном сигнале случаются излишне большим числом выборок.

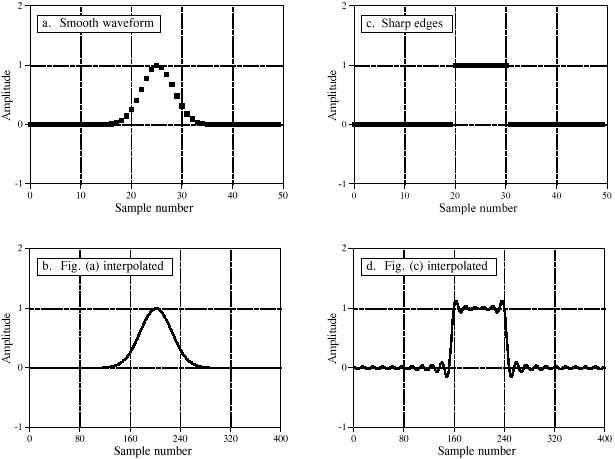
            Главная особенность этой методики - то, что интерполируемый сигнал составлен точно из той же самой частоты, что и первоначальный сигнал. Это может или не может обеспечи-вать хорошим пригодным(удобным для анализа) в домене времени. Например, рис. 10-13

(a) и (b) показано 50 выборок сигнала, интерполируемых в 400 выборок сигнала этим ме-тодом. Интерполяция есть сглаживание пригодное между первоначальными точками, много, как будто подпрограмма вычерчивания кривой использовалась. На сравнении, (c) и

(d) показывают другой пример, где домен времени – беспорядок(путаница )! Колебатель-ное поведение, показанное в (d) возникает в гранях(фронтах) или других нарушениях в сигнале. Это также включает любой разрыв между нулевой выборкой и N -1, так как до-мен времени рассмотрен как являющийся круговым( циклическим ). Это последейст-вие(выброс на фронте импульса; избыточный отклик на ступенчатое воздействие) в раз-рывах называется эффектом Гиббса, и обсужден в главе 11. Другая методика интерполя-ции частотного домена представлена в главе 3, (до)прибавляя нули между выборками до-мена времени и низкочастотную фильтрацию.

5.    Умножение Сигналов (Амплитудная Модуляция)

6.    Преобразование Фурье(трансформанта Фурье) дискретное Время

7.    Отношение Парсевала