1.Cтруктурное
и кинематическое исследование механизма.
Цель и задачи исследования.
1.Провести структурное исследование механизма.
2.По указанным в задании данным ,а также по принятому масштабу длин КL
вычертить двенадцать равноотстоящих (по входному звену) совмещенных положений
механизма. При этом в качестве нулевого положения механизма, от которого
начинается отсчет движения, принимается крайнее положение, занимаемое входным
звеном механизма, где начинается рабочий ход.
3.Для двенадцати положений механизма построить планы скоростей и по ним
определить абсолютные, относительные линейные и угловые скорости звеньев.
4.Для трех положений механизма, одно из которых является крайним, построить
планы ускорений и по ним определить абсолютные, относительные линейные и
угловые ускорения звеньев.
1.1. Структурное исследование механизма.
Кинематическая схема механизма представлена на задании.
Рассматривая последовательно звенья и кинематические пары, даем их
характеристику , заполняя таблицу 1.
Табл.1.
|
№ |
№ звеньев |
Наименование звеньев |
Наименование кинематической пары |
Точка приложения |
|
1 |
1-0 |
кривошип-стойка |
вращательная |
0 |
|
2 |
1-2 |
кривошип-шатун |
1-1 |
А |
|
3 |
2-3 |
шатун-ползун |
1-1 |
В |
|
4 |
3-0 |
ползун-стойка |
поступательная |
В |
|
5 |
1-4 |
кривошип-шатун |
вращательная |
С |
|
6 |
4-5 |
шатун-ползун |
1-1 |
D |
|
7 |
5-0 |
ползун-стойка |
поступательная |
D |
Все кинематические пары, представленные в таблице, пятого класса,
низшие.
Определяем степень подвижности механизма. Так как механизм плоский, то
используем формулу П. Л. Чебышева .
w = 3 n – 2 p 5 – p4
где n =5 - число подвижных звеньев;
p 5 =7 - число кинематических пар пятого класса( низших);
p 4 =0 - число кинематических пар четвертого класса(высших)
Подставим эти данные в формулу П .Л .Чебышева и находим
W =3• 5- 2• 7 - 0=1 .
Равенство W =1 означает, что в рассматриваемом
механизме достаточно задать закон движения только одному звену( в данном случае
звену I, которое является входным), чтобы закон движения остальных звеньев
механизма был вполне определенным.
Определяем класс и формулу строения механизма. Для этого раз¬ложим механизм на
группы Ассура. Согласно заданию звену 1 (Кривошипу С 0 А) задана угловая скорость w1
.Следовательно, звено I вместе со стойкой 0 составляют начальный механизм первого
класса. Его обозначают I(0,1).Оставшиеся звенья 2,3,4,5 механизма составляют
структурные группы Ассура - группы звеньев с нулевой степенью подвижности).
Разложение механизма на группы Ассура обычно осуществляется методом попыток и
его следует начинать с последней наиболее отдаленной от входного звена группы
.Простейшая группа Ассура представляет собой сочетание двух звеньев и трёх
кинематических пар. Для нашего механизма такой группой может быть группа звеньев
4 и 5.Степень подвижности этой группы
w = 3 n – 2 p 5 = 3 • 2 - 2 • 3=0, а степень подвижности оставшейся части
механизма w = 3 n – 2 p 5 = 3 • 3 – 2 • 4 =1. Следовательно, первая структурная
группа не изменяет степени подвижности механизма и выделена нами верно.
Согласно классификации Л. В. Ассура это есть структурная группа второго класса,
второго порядка, 2 вида. Её обозначают  (4,5).Вторую структурную группу
составляют звенья 2 и 3.Степень подвижности группы
(4,5).Вторую структурную группу
составляют звенья 2 и 3.Степень подвижности группы
w = 3 n – 2 p 5 = 3 • 2 - 2 • 3=0, а степень подвижности оставшейся части
механизма(звена I и стойки 0) w = 3 n – 2 p 5 = 3 • 1 - 2 • 1= 1
Следовательно, и эта группа выделена нами верно. Это есть структурная группа
Ассура второго класса, второго порядка, 2 вида. Её обозначают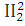 (2,3).
(2,3).
Класс механизма определяется наивысшим классом структурной группы Ассура. На
основании проведенного исследования можем заключить, что данный механизм
является механизмом второго класса.
Формула строения механизма: I(1,0) 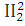 (2,3)
(2,3) 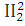 (4,5)
(4,5)
В табл.2 приведен механизм, разложенный на группы Ассура( при разложении
механизма на группы Ассура обязательно следует соблюдать взаимное расположение
звеньев)
|
Структ. Группы |
Изображение структурной Группы |
№ звеньев |
Класс |
порядок |
вид |
|
Первая Структ. Группы |
|
4,5 |
II |
2 |
2 |
|
Вторая Структ. Группы |
|
2,3 |
II |
2 |
2 |
|
Начальный Механизм |
|
1,0 |
I |
- |
- |
1.2. Построение планов положений механизма.
Кривошип С0А вращается по часовой стрелке,
шатуны АВ и СD
(звенья2,4) совершают сложное перемещение, ползуны В, D (звенья 2,4) движутся возвратно–поступательно
в горизонтальном направлении.По исходным данным вычерчиваем двенадцать планов
положений механизма в масштабе К L
Действительная длина кривошипа равна 0,05 м. .
Пусть на чертеже плана механизма эта длина изобразится отрезком 25 мм.
Тогда масштабный коэффициент плана 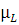 =
=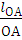 =
= =
=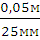 =0,002
=0,002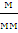
Чертежные размеры остальных звеньев в выбранном масштабе соответственно
определяются
ОА = ОС = 0,05 м (25 мм на чертеже)
АВ = СD = 0,2 м (100мм на чертеже)




 =
=  =
=  (AB) =
(AB) = * 0,2 = 0,066 м (33 мм на чертеже)
* 0,2 = 0,066 м (33 мм на чертеже)
Для построения двенадцати положений механизма отмечаем на чертеже положения
неподвижных элементов кинематических пар : шарнира О и направляющей ползунов B и D. (горизонтальной); проводим окружность
радиусом ОА = ОС = 25мм
Определяем нулевое положение механизма, при котором кривошип ОА и шатун АВ
вытягиваются в одну линию; при этом делим траекторию кривошипа на 12 равных
частей и достраиваем остальные положения оставшихся точек механизма.
1.3. Построение планов скоростей.
Определение линейных скоростей точек механизма начинаем с входного звена 1
.Модуль скорости точки A кривошипа, совершающего вращательное движение, определим по
формуле
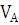 = w1
= w1 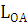 =490 * 0,05 = 24,5 м/с
=490 * 0,05 = 24,5 м/с
Где w1 – угловая скорость вращения кривошипа.
w1 = 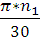 = 490
= 490 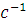 по заданию n 1 -
число оборотов кривошипа.
по заданию n 1 -
число оборотов кривошипа.
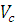 =
=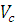 ;
; 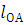 =
=  ; СОА = с
; СОА = с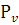 а =
а = 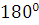
Вектор скорости 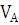 направлен перпендикулярно кривошипу ОА в сторону его вращения. Далее
определяем скорости других точек механизма.
направлен перпендикулярно кривошипу ОА в сторону его вращения. Далее
определяем скорости других точек механизма.
Для этого составляем векторные уравнения (или системы векторных уравнений)
,связывающих неизвестные скорости точек с известными.
При этом векторы, известные по модулю и направлению, подчеркиваем двумя
чертами, а известные только по направлению – одной чертой.


 Скорость точки В найдем по соотношению
Скорость точки В найдем по соотношению


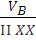 =
= 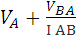 ; XX- горизонтальная ось.
; XX- горизонтальная ось.
Определяем скорость точки 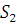 по теореме подобия.
по теореме подобия.

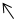
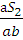 =
= 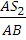 =
= 
на плане скоростей на плане положения механизма


 Скорость точки D определим по соотношению:
Скорость точки D определим по соотношению:


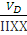 =
= 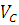 =
= 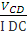
Изображая скорость точки A кривошипа на плане скоростей отрезком 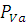 ,определим значение масштабного коэффициента плана скоростей
,определим значение масштабного коэффициента плана скоростей
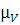 =
= 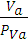 =
= 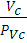 =
= 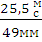 = 0,50
= 0,50 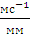
где P V – полюс плана скоростей. Планы скоростей изобразим двумя чертежами : на
одном построим планы скоростей для четных положений механизма, а на другом –для
нечетных.
Угловые скорости звеньев.
w1 = 490 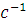 = const
= const
w2 = 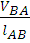 =
= 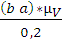 = (ba) * 2,5
= (ba) * 2,5
w4 =  =
= 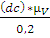 = (dc) * 2,5
= (dc) * 2,5
w3 =w5=0,т.к. звенья движутся поступательно.
Для определения направления угловой скорости , например, 2 звена для
определенного положения механизма, необходимо мысленно перенести вектор
скорости для данного положения механизма  в точку B и пронаблюдать вращение звена 2
относительно точки
в точку B и пронаблюдать вращение звена 2
относительно точки 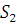 под действием данного вектора.
под действием данного вектора.
Составляем таблицу.
Табл.3.
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
|
|
ba, мм |
49 |
45 |
26 |
0 |
26 |
43 |
49 |
44 |
24 |
0 |
27 |
42 |
|
w2 |
122 |
112 |
65 |
0 |
65 |
107 |
122 |
110 |
60 |
0 |
67 |
105 |
|
|
0 |
18 |
36 |
49 |
46 |
27 |
0 |
30 |
48 |
49 |
35 |
19 |
|
|
0 |
9 |
18 |
24,5 |
23 |
13,5 |
0 |
15 |
24 |
24,5 |
17,5 |
9,5 |
|
dc, мм |
49 |
45 |
26 |
0 |
26 |
43 |
49 |
44 |
24 |
0 |
27 |
42 |
|
w4, |
122 |
112 |
65 |
0 |
65 |
107 |
122 |
110 |
60 |
0 |
67 |
105 |
|
|
0 |
18 |
36 |
49 |
46 |
27 |
0 |
30 |
48 |
49 |
35 |
19 |
|
|
0 |
9 |
18 |
24,5 |
23 |
13,5 |
0 |
15 |
24 |
24,5 |
17,5 |
9,5 |
C плана скоростей находим скорости точек
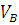 = (
= (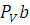 ) *
) * 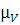
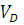 = (
= (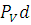 ) *
) * 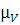
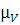 = 0,5
= 0,5 
1.4.Построение планов ускорений.
Прежде всего необходимо определить ускорение начального звена 1. Так как
кривошип 1 вращается с постоянной угловой скоростью w1,то Точка A будет иметь только нормальное ускорение,
модуль которого равен








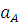 =
= 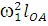 =
= 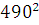 * 0,05 = 12005
* 0,05 = 12005 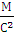
Это ускорение направлено вдоль звена OA от точки A к точке O. Для определения ускорения точки B составим систему векторных уравнений.
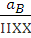 =
=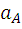 +
+ +
+ ;
;  =
=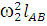
Определяем ускорение точки C .


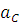 =
=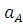 ; OA=OC ; СОА = с
; OA=OC ; СОА = с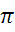 a =
a = 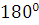
 Найдем ускорение точки D.
Найдем ускорение точки D.







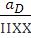 =
=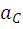 +
+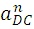 +
+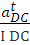 ;
; 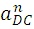 =
=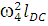 ;
;
Вектор нормального ускорения  направлен от точки B к точки A.
направлен от точки B к точки A.
Вектор нормального ускорения 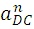 направлен от точки D к точки C.
направлен от точки D к точки C.
При этом векторы, известные по модулю и направлению, подчеркиваем двумя
чертами, а известные только по направлению – одной чертой.
Масштабный коэффициент планов ускорений 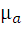 =
= 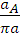 =
= 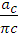 =
=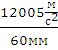 =200
=200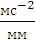
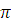 – полюс плана ускорений.
– полюс плана ускорений.
Для определения углового ускорения, например, для 2 звена для определенного
положения механизма необходимо мысленно с плана ускорений перенести вектор тангенциального
ускорения 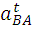 в точку B механизма и пронаблюдать вращение звена 2 под действием этого вектора
относительно точки
в точку B механизма и пронаблюдать вращение звена 2 под действием этого вектора
относительно точки 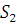 .
.
Таблица 4
|
№6 |
№3 |
№9 |
|
|
|
0 |
62 |
62 |
|
|
0 |
12400 |
12400 |
|
|
0 |
62000 |
62000 |
|
|
75 |
15 |
15 |
|
|
15000 |
300 |
300 |
|
|
0 |
62 |
62 |
|
|
0 |
12400 |
12400 |
|
|
0 |
62000 |
62000 |
|
|
75 |
15 |
15 |
|
|
15000 |
300 |
300 |
Угловые ускорения звеньев:
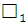 = 0 т. к
= 0 т. к  = const
= const
 =
= 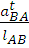
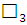 =
=  = 0 т. к
= 0 т. к 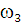 =
= 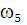 = 0
= 0
 =
= 
С планов ускорений находим ускорения точек B и D:
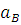 = (
= (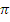 b) *
b) * 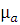
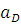 = (
= (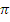 d) *
d) * 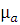
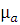 = 200
= 200
Для 6 положения:
 =
=  * 0,2 = 2977
* 0,2 = 2977 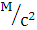 ( 15 мм)
( 15 мм)
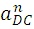 =
=  * 0,2 = 2977
* 0,2 = 2977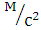 ( 15 мм)
( 15 мм)
Для 3 положения:
 = 0 * 0,2 = 0
= 0 * 0,2 = 0 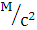 ( 0 мм)
( 0 мм)
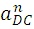 = 0 * 0,2 = 0
= 0 * 0,2 = 0 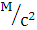 ( 0 мм)
( 0 мм)
Для 9 положения
 = 0 * 0,2 = 0
= 0 * 0,2 = 0 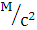 ( 0 мм)
( 0 мм)
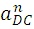 = 0 * 0,2 = 0
= 0 * 0,2 = 0 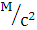 ( 0 мм)
( 0 мм)
1.5. Построение диаграмм выходного звена.
Переходим к построению кинематических диаграмм выходного звена.
График пути строим на основе планов положений механизма. Начало координат
системы S O t условно совмещаем с точкой 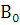 , соответствующей крайнему правому положению точки B. На оси абсцисс задаёмся отрезком
, соответствующей крайнему правому положению точки B. На оси абсцисс задаёмся отрезком 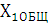 , соответствую¬щим времени одного оборота кривошипа. Принимаем
, соответствую¬щим времени одного оборота кривошипа. Принимаем 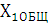 = 240 мм(при выполнении графических работ на диете формата А1 рекомендуется
принимать
= 240 мм(при выполнении графических работ на диете формата А1 рекомендуется
принимать 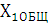 = 240 мм).Этот отрезок делим на двенадцать равных частей в
соответствии с делением траектории подвижного шарнира кривошипа СОА. Из точек
деления проводим ординаты и нумеруем их соответственно номеру положения
кривошипа 0,1,2,...,11. На каждой ординате откладываем путь, пройденный точкой B от нулевого положения
= 240 мм).Этот отрезок делим на двенадцать равных частей в
соответствии с делением траектории подвижного шарнира кривошипа СОА. Из точек
деления проводим ординаты и нумеруем их соответственно номеру положения
кривошипа 0,1,2,...,11. На каждой ординате откладываем путь, пройденный точкой B от нулевого положения 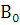 до рассматриваемого положения.
до рассматриваемого положения.  = 0,002 м/мм
= 0,002 м/мм
Масштабный коэффициент времени:
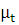 =
= =
= 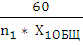 =
= 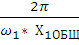 =
=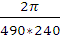 = 0,000053
= 0,000053 
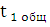 - время, в течении которого кривошип совершает один оборот;
- время, в течении которого кривошип совершает один оборот;
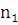 ,
, 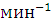 - число оборотов кривошипа в минуту.
- число оборотов кривошипа в минуту.
Угловая скорость кривошипа w1 = 490 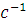 по заданию.
по заданию.
 Диаграмму скорости строим дифференцированием графика пути в
следующем порядке:
Диаграмму скорости строим дифференцированием графика пути в
следующем порядке:
- на каждом участке времени t кривую заменяем ломаной линией ;
- в новой системе координат выбираем точку на расстоянии h1 (при выполнении
графических работ на листе формата AI рекомендуется принимать h1 =40...60 мм) и
проводим через неё прямые, параллельные соответствующим хордам до пересечения с
осью ординат;
- из точек пересечения проводим горизонтальные линии до пересечения с
вертикальными линиями ,проведенными через середины отрезков времени.
- точки пересечения 1”,2”,…….11” соединяем плавной кривой и получаем график
скорости выходного звена.
Масштабный коэффициент графика скорости
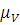 =0,5
=0,5 
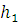 =
= 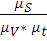 =
= 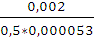 = 75 мм
= 75 мм
Дифференцируя аналогичным образом график скорости, получим график ускорений. Масштабный коэффициент графика
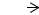
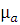 = 200
= 200
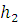 =
= 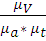 =
= 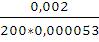 = 47 мм
= 47 мм
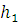 и
и 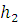 – полюсное расстояние для графического дифференцирования.
– полюсное расстояние для графического дифференцирования.
2. Проектирование кулачкового механизма.
ИСХОДНЫЕ ДАННЫЕ :
Угол удаления: 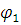 =
=  =
=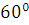 = 1,05 рад
= 1,05 рад
Угол верхнего стояния: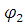 =
= 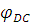 = 0
= 0
Угол приближения: 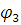 =
= 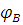 =
= 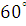 =1,05 рад
=1,05 рад
Максимальный угол давления в кулачковом механизме:
 =
= 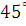 =
= 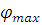
Ход толкателя кулачкового механизма h = 9 мм =0,009 м
Масштабный коэффициент оси абсцисс
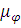 =
=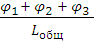 =
=  = 0,0087
= 0,0087 
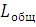 – расстояние по оси Х на графиках, соответствующее рабочему углу
кулачка.
– расстояние по оси Х на графиках, соответствующее рабочему углу
кулачка.
Полюсное расстояние Н = 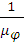 =
= 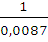 = 114 мм
= 114 мм
Эта величина Н обеспечивает приемлемую высоту ординат диаграмм и их одинаковое
значение.
Максимум на графике ускорений
при удаление: ± 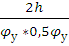 = ±
= ±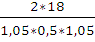 =±65 мм
=±65 мм
при приближение: ± 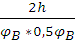 = ±
= ±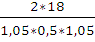 =±65 мм
=±65 мм
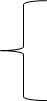 h =
h = 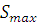 = 18 мм на чертеже
= 18 мм на чертеже
Максимум на графике скорости
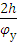 =
= 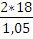 = 34 мм
= 34 мм
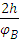 =
= 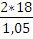 = 34 мм
= 34 мм
Максимум на графике пути
h = 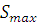 = 18 мм
= 18 мм
Угол удаления и приближения (возвращения) кулачка разделим для графических построений на 6 равных частей. Результаты построения графиков по точкам представим в табличной форме.
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
|
S |
0 |
2 |
5 |
9 |
13 |
16 |
18 |
16 |
13 |
9 |
5 |
2 |
0 |
|
dS/d |
0 |
11 |
23 |
34 |
23 |
11 |
0 |
-11 |
-23 |
-34 |
-23 |
-11 |
0 |
|
|
65 |
65 |
65 |
65 |
-65 |
-65 |
-65 |
-65 |
-65 |
-65 |
65 |
65 |
65 |
Масштабные коэффициенты:
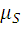 =
= 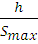 =
= 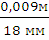 = 0,0005
= 0,0005 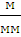
h - ход толкателя кулачкового механизма в метрах ( по заданию)
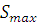 - ход толкателя кулачкового
механизма в миллиметрах на графиках.
- ход толкателя кулачкового
механизма в миллиметрах на графиках.
 = 0,005
= 0,005 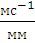 ;
; 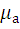 = 0,005
= 0,005 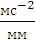 ;
;
График скорости строится графическим интегрированием графика ускорений с
полюсным расстоянием Н , график пути графическим интегрированием графика скорости
с полюсным расстоянием Н.
Для определения минимального радиуса кулачка строим диаграмму
S - 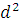 S/d
S/d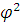 методом исключения угла
методом исключения угла 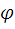 в масштабе
в масштабе 
 =
= 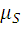 = 0,0005
= 0,0005 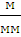
Минимальный радиус кулачка:
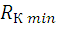 = 70 мм *
= 70 мм * 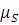 = 70 мм *0,0005
= 70 мм *0,0005 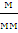 = 0,035 м
= 0,035 м
Далее строим профиль кулачка, зная величины его фазовых углов.




































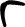


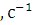

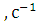
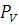 d,мм
d,мм ,
, 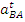 , мм
, мм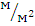
 ,
,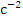
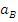 ,
,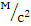
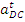 , мм
, мм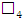 ,
,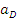 ,
,
 (zip - application/zip)
(zip - application/zip)










