Текст:

Содержание

1) Введение…………………………………………………………....…4

2) Модель………………………………………………………………...6

a. Связь с внешней средой……………………………………….7

b. Наблюдения………………………………………………….…7

3) Типы шкал………………………………………………………….…9

a. Номинальная шкала…………………………………………....9

b. Ординальная шкала…………………………………………....9

c. Интервальная шкала………………………………………….10

4) Типы моделей………………………………………………………..11

5) Виды моделей………………………………………………………..13

6) Информационное моделирование………………………………….14

a. Иерархические модели……………………………………….14

b. Сетевые информационные модели…………………………..15

7) Компьютерное моделирование……………………………………..16

8) Этапы и цели компьютерного моделирования………………….....20

9) Заключение…………………………………………………..……….22

10) Список используемых источников…………………...……………23

11) Ведомость работы

Введение

Моделирование является одним из способов познания мира.

Понятие моделирования достаточно сложное, оно включает в себя огромное разнообразие способов моделирования: от создания натуральных моделей (уменьшенных и или увеличенных копий реальных объектов) до вывода математических формул.

Для различных явлений и процессов бывают уместными разные способы моделирования с целью исследования и познания.

Объект, который получается в результате моделирования, называется моделью. Должно быть понятно, что это совсем не обязательно реальный объект. Это может быть математическая формула, графическое представление и т.п. Однако он вполне может заменить оригинал при его изучении и описании поведения.

Хотя модель и может быть точной копией оригинала, но чаще всего в моделях воссоздаются какие-нибудь важные для данного исследования элементы, а остальными пренебрегают. Это упрощает модель. Но с другой стороны, создать модель – точную копию оригинала – бывает абсолютно нереальной задачей. Например, если моделируется поведение объекта в условиях космоса. Можно сказать, что модель – это определенный способ описания реального мира.

Моделирование проходит три этапа:

1. Создание модели.

2. Изучение модели.

3. Применение результатов исследования на практике и/или формулирование теоретических выводов.

Видов моделирования огромное количество. Вот некоторые примеры типов моделей:

Математические модели. Это знаковые модели, описывающие определенные числовые соотношения.

Графические модели. Визуальное представление объектов, которые настолько сложны, что их описание иными способами не дает человеку ясного понимания. Здесь наглядность модели выходит на первый план.

Имитационные модели. Позволяют наблюдать изменение поведения элементов системы-модели, проводить эксперименты, изменяя некоторые параметры модели.

Над созданием модели могут работать специалисты из разных областей, т.к. в моделировании достаточно велика роль межпредметных связей.

Модель

Модель – это абстрактное (идеализированное) отображение функционирования физической системы с той или иной точки зрения. Моделирование систем возможно в силу принципа моделируемости, который заключается в следующем: f систему можно представить конечным множеством моделей, каждая из которых отражает определенную грань еѐ сущности; f модель, ориентированная на отображение определенных свойств системы, всегда проще самой системы (принцип гомоморфизма ); f создание полной модели системы вообще бесполезно, т.к. в силу теоремы Тьюринга,

С учетом сказанного одна и та же физическая система может иметь множество моделей своего функционирования. Если несколько разных моделей характеризуются одинаковым набором входных и выходных величин и одинаково реагируют на внешние воздействия, то они называются изоморфными . Среди изоморфных моделей можно выбрать оптимальную по тому или иному критерию. Перед выбором модели необходимо определиться с границами моделируемой системы, набором наблюдаемых параметров (базой), входными и выходными воздействиями системы. В качестве базы может быть выбрано время, пространство, другие физические характеристики или их группа. В качестве группы может выступать набор каких-нибудь свойств, например: форма, цвет, качество и т.п. Требования к базовым параметрам: f базовые параметры должны быть применимы ко всем свойствам системы; f база должна отвечать целям моделирования физической системы; f наблюдение за входными и выходными воздействиями системы должно однозначно определяться базой.

Связь с внешней средой

Связи модели с внешней средой можно подразделить на входные и возмущающие. Входные связи являются контролируемыми параметрами, возмущающие – неконтролируемыми. Независимо от типа связи, они бывают трех видов: f детерминированные, значения которых заранее известны; f случайные, с известным законом распределения; f неопределенные, для которых известна только область действия, но неизвестны законы распределения или даже их вероятностные характеристики. Неопределенные связи отражают недостаточную изученность физической системы. На связи модели с внешней средой могут быть наложены ограничения. Связи и свойства системы актуализируются с помощью наблюдений.

Наблюдения

В качестве наблюдаемых необходимо выбирать те свойства, которые изменяются в процессе функционирования системы. Если свойство в процессе функционирования не изменяется, то бесполезно вести за ним наблюдение. Для наблюдения свойств системы используются устройства, обычно называемые измерительными приборами или инструментами. Наблюдаемое свойство и результат наблюдения связаны между собой зависимостью: Q= Af (u)+E, где: f(u) – наблюдаемое свойство; Q – результат наблюдения; А – линейный оператор, описывающий измерительный прибор (при A = I, где I – единичный оператор, речь идет об идеальном приборе, не искажающем наблюдаемое свойство); E – погрешности измерения, называемые шумом и понимаемые как случайный вектор с нулевым математическим ожиданием.

Любой измерительный инструмент должен уметь взаимодействовать с физической системой и преобразовывать это взаимодействие в вид, непосредственно отображающий состояние соответствующего наблюдаемого воздействия. Добиться этого можно только при идеальной характеристике прибора. Реальные приборы искажают наблюдаемое свойство. Компенсировать искажения можно при использовании измерительно-вычисли-тельных комплексов. В этом случае приведенное выше выражение преобразуется к виду: RQ=RAf(u)+RE где: R – оператор, выбирающийся из условий линеаризации характеристик прибора (RA) и минимизации погрешности RE.

Процедура наблюдения представляет собой набор инструкций, определяющих то, как следует использовать инструмент в различных условиях и каким образом интерпретировать результат /1 с.51/. Совокупность инструмента и набора инструкций будем называть каналом наблюдения, который характеризуется шкалой.

Типы шкал

Шкалой называется тройка {K,Q,f}, где f – конкретный способ "гомоморфного" (т.е. однозначного в одну сторону) отображения K на Q (например, отображение веса в граммах). Если с помощью преобразования f отображение f можно взаимно однозначно перевести в отображение f (f = ff; f = f-–1f), то шкалы считаются принадлежащими к одному типу (например: вес в граммах, килограммах, тоннах). Необходимо учитывать, что в канале наблюдения могут использоваться различные типы шкал (номинальные, ординальные, интервальные).

Номинальная шкала (шкала наименований) основана на любом приписывании тех или иных символов (знаков) проведенному наблюдению, которые играют простую роль имен. Имя служит для идентификации множества наблюдений. Причем каждому множеству приписывается свое имя. Разные имена приписываются разным множествам, и наоборот – одно имя приписывается всем элементам одного множества. Шкала может быть категорезированной или нет. В категорезированной шкале заранее известно количество множеств (категорий, классов, рангов, градаций), на которые может быть разбито наблюдение. В некатегорезированной шкале количество множеств разбиения наблюдения заранее неизвестно. Основной операцией с данным типом шкал является операция "равенства", т.е. с помощью номинальной шкалы можно установить только – относится ли данное наблюдение к множеству с заданным именем или нет. Данный тип шкал остается инвариантным относительно замен имен множеств при сохранении целостности самих множеств.

Ординальная шкала, или шкала порядка, предполагает упорядочение наблюдений относительно какого-либо их параметра и допускает действие операций "равенства" и "больше – меньше". С помощью шкалы порядка можно определить принадлежность наблюдения к тому или иному множеству и установить порядок следования множеств. Ординальная шкала может быть категорезированной или нет. Шкала остается инвариантной относительно всякого монотонного преобразования. Иногда выделяют частично упорядоченные шкалы, в которых отношение "больше –меньше" действительно только для некоторых элементов шкалы.

Интервальная шкала, или метрическая, предполагает наличие единицы измерения и какого-то начала и допускает все арифметические операции, если они относятся к интервалам между двумя шкальными значениями. В этих шкалах можно сравнивать наблюдения между собой.

Типы моделей

Модели можно подразделить на типы и виды. Один и тот же тип модели может иметь различный вид. Используются следующие типы моделей:

Аналитические, в которых процессы в системе отображаются некоторыми функциональными зависимостями и могут быть получены в явном виде для искомых характеристик или получены численным методом при задании конкретных начальных данных, или получены качественные характеристики для некоторых свойств;

Имитационные, которые воспроизводят (имитируют) функционирование всей системы через функционирование её элементов с соблюдением временной, пространственной и другой последовательности взаимодействия элементов и качеств связи между ними. Имитационные модели используются в тех случаях, когда отсутствует целостная теория моделируемой системы. Такая модель позволяет достаточно просто учитывать такие факторы, как наличие дискретных и непрерывных элементов и связей в системе, нелинейные характеристики элементов и связей, случайные воздействия, мнения экспертов. В настоящее время имитационное моделирование – наиболее эффективный метод исследования больших систем;

Кибернетические, в которых отсутствует непосредственное подобие физических процессов, происходящих в системе. Система отображается в виде "черного ящика" с рядом входов и выходов и исследуются его реакции на внешние воздействия. Целью исследования является установление зависимостей между входами и выходами;

Интерактивные (игровые), которые предполагают наличие конфликта и различных стратегий их преодоления. Конфликтом называются взаимно-противоречивые альтернативы решения задачи, которые не могут быть осуществлены одновременно в силу ограниченности ресурса, в том числе и информационного. Стратегии решения задачи могут меняться в процессе моделирования. Основными решаемыми задачами являются следующие

Для интерактивных моделей характерно, что в качестве некоторых элементов системы включены люди с их понятием стратегии, тактики и реакцией на входные воздействия и внутренние состояния системы. При этом предполагается, что у каждого человека имеется несколько стратегий или прототипов поведения, которые они выбирают исходя из сложившейся ситуации. Первоначально, игровые модели использовались для анализа конфликтов и попытки их разрешения. В настоящее время игровые модели широко используются в исследованиях социальных систем и раскрытия законов их функционирования.

В зависимости от полноты знаний о физической системе, выбирается тот или иной тип модели. Типы моделей перечислены сверху вниз в порядке убывания наших знаний о системе. Если мы о системе знаем мало, то пользуемся интерактивной моделью для получения дополнительных знаний. Далее переходим к кибернетической модели, получаем знания о структуре и внутренних связях. Затем переходим к имитационной, корректируя внутренние функциональные зависимости элементов и видов связи; и, наконец, получаем аналитическую модель системы.

Виды моделей

Модели, их элементы и модули бывают следующих видов: детерминированные, в модели отсутствуют случайные воздействия (пример: падение тела);

стохастические, которые отображают вероятностные процессы и явления (пример: броуновское движение молекул);

статические, отображающие поведение системы в какой-либо момент времени или вне времени (пример: оптико-электронные преобразователи);

динамические, отображающие поведение системы во времени (пример: колебания маятника, тепловые процессы);

дискретные, в которых явно выражен дискретный характер входных и выходных воздействий, и/или связей, и/или внутренних состояний (например: системы массового обслуживания);

непрерывные, в которых дискретный характер связей не выражен в силу уровня представления системы (например: волновая оптика)

линейные (нелинейные) /27 с.43/, в которых выход (и/или состояния) системы линейно (нелинейно) зависит от входных воздействий (и/или состояний системы). Линейность может быть естественным свойством системы или только свойством модели (например: линеаризация модели оптико-электронных систем достигается путем использования однородного преобразования координат /28/). Часто приходится сталкиваться с ситуацией, когда в модели одновременно используются элементы и модули различных видов (статические и динамические, дискретные и аналоговые, линейные и нелинейные и т.д.).

Информационное моделирование

Табличные модели. Одним из наиболее часто используемых типов информационных моделей является таблица, которая состоит из строк и столбцов.

Построим, например, табличную информационную модель, отражающую стоимость отдельных устройств компьютера. Пусть в первом столбце таблицы содержится перечень объектов (устройств), входящих в состав компьютера, а во втором – их цена.

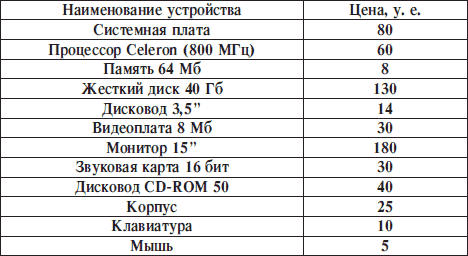
Рисунок 9.2. Информационная табличная модель

С помощью таблиц создаются информационные модели в различных предметных областях. Широко известно табличное представление математических функций, статистических данных, расписаний поездов и самолетов, уроков и т. д.

Табличные информационные модели проще всего формировать и исследовать на компьютере посредством электронных таблиц и систем управления базами данных.

Иерархические модели

Нас окружает множество различных объектов, каждый из которых обладает определенными свойствами. Однако некоторые группы объектов имеют одинаковые общие свойства, которые отличают их от объектов других групп.

Группа объектов, обладающих одинаковыми общими свойствами, называется классом объектов. Внутри класса могут быть выделены подклассы, объекты которых обладают некоторыми особенными свойствами, в свою очередь, подклассы можно делить на еще более мелкие группы и т. д. Такой процесс называется процессом классификации.

При классификации объектов часто применяются информационные модели, которые имеют иерархическую (древовидную) структуру. В иерархической информационной модели объекты распределены по уровням, причем элементы нижнего уровня – входят в состав одного из элементов более высокого уровня. Например, весь животный мир рассматривается как иерархическая система (тип, класс, отряд, семейство, род, вид), для информатики характерна иерархическая файловая система и т. д.

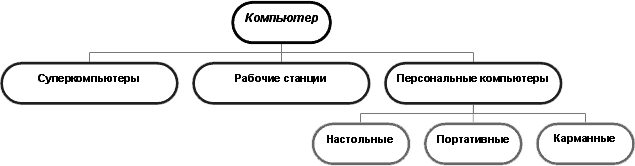
Рисунок 9.3. Информационная иерархическая модель

На рисунке 9.3 изображена информационная модель, которая позволяет классифицировать современные компьютеры. Полученная информационная структура напоминает дерево, которое растет сверху вниз (именно поэтому такие информационные модели называют иногда древовидными). В структуре четко просматриваются три уровня: от первого, верхнего, имеющего один элемент Компьютеры, мы спускаемся до третьего, нижнего, имеющего три элемента Настольные, Портативные, Карманные.

Сетевые информационные модели

Сетевые информационные модели применяются для отражения систем со сложной структурой, в которых связь между элементами имеет произвольный характер.

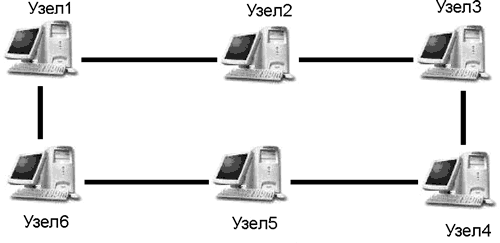
Рисунок 9.4. Сетевая информационная модель

Компьютерное моделирование

Язык – это знаковая система, используемая для целей коммуникации и познания.

Языки можно разделить на естественные и искусственные. Естественные (обычные, разговорные) языки складываются стихийно и в течение долгого времени. Искусственные языки создаются людьми для специальных целей или для определенных групп людей (язык математики, морской язык, языки программирования и т. д.). Характерной их особенностью является однозначная определенность их словаря, правил образования выражений и конструкций (строго формализованы). В естественных языках они – частично формализованы.

Каждый язык характеризуется:

• набором используемых знаков;

• правилом образования из этих знаков языковых конструкций;

• набором синтаксических, семантических и прагматических правил использования языковых конструкций.

Алфавит – это упорядоченный набор знаков, используемых в языке.

В информатике нас прежде всего интересуют модели, которые можно создавать и исследовать с помощью компьютера. С помощью компьютера можно создавать и исследовать множество объектов: тексты, графики, таблицы, диаграммы и пр. Компьютерные технологии накладывают все больший отпечаток на процесс моделирования, поэтому компьютерное моделирование можно рассматривать как особый вид информационного моделирования.

В последние годы благодаря развитию графического интерфейса и графических пакетов, широкое развитие получило компьютерное, структурно-функциональное моделирование. Суть имитационного компьютерного моделирования заключена в получении количественных и качественных результатов функционирования моделируемой системы по имеющейся модели. Качественные выводы, получаемые по результатам анализа модели, позволяют обнаружить неизвестные ранее свойства сложной системы: ее структуру, динамику развития, устойчивость, целостность и пр. Количественные выводы в основном носят характер прогноза некоторых будущих или объяснение прошлых значений параметров, характеризующих систему.

Цели компьютерного моделирования могут быть различными, но чаще всего это получение данных, которые могут быть использованы для подготовки и принятия решений экономического, социального, организационного или технического характера. Положено начало использованию компьютера даже при концептуальном моделировании, где он используется, например, при построении систем искусственного интеллекта.

Таким образом, мы видим, что понятие «компьютерное моделирование» значительно шире традиционного понятия «моделирование на ЭВМ» и нуждается в уточнении, учитывающем сегодняшние реалии.

Начнем с термина «компьютерная модель».

В настоящее время под компьютерной моделью чаще всего понимают:

• условный образ объекта или некоторой системы объектов (или процессов), описанный с помощью взаимосвязанных компьютерных таблиц, блок-схем, диаграмм, графиков, рисунков, анимационных фрагментов, гипертекстов и т. д. и отображающий структуру и взаимосвязи между элементами объекта. Компьютерные модели такого вида мы будем называть структурно-функциональными;

• отдельную программу, совокупность программ, программный комплекс, позволяющий с помощью последовательности вычислений и графического отображения их результатов воспроизводить (имитировать) процессы функционирования объекта, системы объектов при условии воздействия на объект различных (как правило, случайных) факторов. Такие модели мы будем далее называть имитационными моделями.

Компьютерное моделирование – метод решения задачи анализа или синтеза сложной системы на основе использования ее компьютерной модели.

Суть компьютерного моделирования заключена в получении количественных и качественных результатов по имеющейся модели. Качественные выводы, получаемые по результатам анализа, позволяют обнаружить неизвестные ранее свойства сложной системы: ее структуру, динамику развития, устойчивость, целостность и др. Количественные выводы в основном носят характер прогноза некоторых будущих или объяснения прошлых значений переменных, характеризирующих систему. Компьютерное моделирование для рождения новой информации использует любую информацию, которую можно актуализировать с помощью ЭВМ.

Основные функции компьютера при моделировании:

• выполнять роль вспомогательного средства для решения задач, решаемых обычными вычислительными средствами, алгоритмами, технологиями;

• выполнять роль средства постановки и решения новых задач, не решаемых традиционными средствами, алгоритмами, технологиями;

• выполнять роль средства конструирования компьютерных обучающе-моделирующих сред;

• выполнять роль средства моделирования для получения новых знаний;

• выполнять роль «обучения» новых моделей (самообучающиеся модели).

Разновидностью компьютерного моделирования является вычислительный эксперимент. Компьютерное моделированиев частности, вычислительный эксперимент становится новым инструментом, методом научного познания, новой технологией также из-за возрастающей необходимости перехода от исследования линейных математических моделей систем.

Предметом компьютерного моделирования могут быть: экономическая деятельность фирмы или банка, промышленное предприятие, информационно-вычислительная сеть, технологический процесс, любой реальный объект или процесс, например, процесс инфляции, и вообще любая Сложная Система. Цели компьютерного моделирования могут быть различными, однако наиболее часто моделирование является, как уже отмечалось ранее, центральной процедурой системного анализа, причем под системным анализом мы далее понимаем совокупность методологических средств, используемых для подготовки и принятия решений экономического, организационного, социального или технического характера.

Компьютерная модель сложной системы должна по возможности отображать все основные факторы и взаимосвязи, характеризующие реальные ситуации, критерии и ограничения. Модель должна быть достаточно универсальной, чтобы по возможности описывать близкие по назначению объекты, и в то же время достаточно простой, чтобы позволить выполнить необходимые исследования с разумными затратами.

Все это говорит о том, что моделирование, рассматриваемое в целом, представляет собой скорее искусство, чем сформировавшуюся науку с самостоятельным набором средств отображения явлений и процессов реального мира.

Процесс исследования поведения какого-либо объекта или системы объектов на компьютере можно разбить на следующие этапы:

• построение содержательной модели;

• построение математической модели;

• построение информационной модели и алгоритма;

• кодирование алгоритма на языке программирования;

• компьютерный эксперимент.

Этапы и цели компьютерного моделирования

Рассмотрим процесс компьютерного математического моделирования, включающий численный эксперимент с моделью.

Моделирование занимает центральное место в исследовании объекта, процесса, явления. Оно позволяет обоснованно принимать решение: как совершенствовать объекты (процессы), надо ли создавать новые, как изменять процессы управления и, в конечном итоге, как менять окружающий мир в лучшую сторону.

Прежде чем браться за какую-либо работу, нужно четко представить себе отправной и конечный пункты деятельности, а также примерные ее этапы. То же можно сказать о моделировании.

Отправной пункт здесь – прототип. Им может быть существующий или проектируемый объект либо процесс.

Конечный этап – принятие решения. На этом этапе мы либо создаем новый объект (процесс), модель которого мы исследовали, либо улучшаем существующий, либо получаем о нем дополнительную информацию.

Рассмотрим процесс решения задачи на компьютере на следующем примере: изучим полет ядра, вытолкнутого легкоатлетом. Построим содержательную модель, в которой рассмотрим движение ядра в поле тяготения Земли. В этой модели рассматриваются только те параметры, которые характеризуют движение ядра (скорость и координаты), и отвлекаемся от других параметров (температура ядра, его цвет и т. д.).

Теперь построим математическую модель, которая основана на некоторых упрощениях, и это делает этап построения математической модели весьма ответственным, ведь неправильно выбранная модель приведет к неверным результатам.

Существующая физическая система описывается с помощью упрощенной математической модели. Ядро является материальной точкой, сопротивлением воздуха, скоростью ветра и параметрами спортсмена пренебрегаем, ускорение свободного падения считаем постоянным g= 9,8 м/с2. Ядро выталкивается спортсменом со скоростью V под углом к горизонту.

Математическая модель описывает объект моделирования с помощью уравнений.

Получим формулы зависимости координат снаряда от времени, учитывая, что по оси X движение равномерное, а по оси Y – равноускоренное:

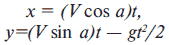
Теперь построим информационную модель и алгоритм. На этом этапе необходимо определить, какие величины являются аргументами, а какие – результатами алгоритма, а также определить тип этих величин. В нашем случае аргументами являются: угол вылета снаряда а, его начальная скорость V и время полета t. Результатом являются координаты X и Y. Все они являются переменными вещественного типа. Построим алгоритм, который позволяет определять значения результатов при различных значениях аргументов. Построенный алгоритм записываем в виде блок-схемы:

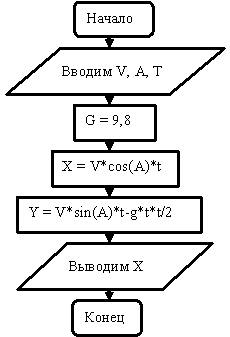
Рисунок 9.5. Блок-схема алгоритма расчета координат полета снаряда

Заключение

Процесс построения модели называют моделированием. Все способы моделирования можно разделить на две большие группы. В одном случае моделью является предмет, воспроизводящий те или иные геометрические, физические и т.п. характеристики оригинала. Это - материальное (физическое) моделирование. Исследование таких моделей - реальные эксперименты с ними.

По иному происходит работа с информационными (идеальными) моделями, являющимися описаниями объектов - оригиналов с помощью схем, графиков, формул, чертежей и т.п. Одним из важнейших видов информационного моделирования является математическое - когда описания формулируются на языке математики. Соответственно, и исследование таких моделей ведется с использованием математических методов. Именно математическим моделированием вы пользуетесь при решении количественных задач на уроках физики и химии.

Математические модели, используемые при решении современных практических задач, настолько сложны, что исследовать их вручную практически невозможно. Приходится прибегать к помощи компьютера. Всякая модель создается для вполне определенной цели, и это в значительной степени определяет ее выбор. Поэтому первое, что необходимо сделать, - поставить задачу, т.е. определить вопросы, ответы на которые мы хотим получить, и необходимые для этого исходные данные.

Во-вторых, нужно выбрать среди законов, которым подчиняется моделируемая система, существенные для поиска ответов на поставленные вопросы. Возможно, придется выдвигать и какие-то предположения. Найденные закономерности следует представить в форме математических соотношений.

Наиболее сложным является имитационное моделирование, позволяющее исследовать сложные системы, прогнозировать будущее их состояние в зависимости от различных стратегий управления.

Моделирование, рассматриваемое в целом, представляет собой скорее искусство, чем сформировавшуюся науку с самостоятельным набором средств отображения явлений и процессов реального мира. Использование компьютерных моделей превращает компьютер в универсальную экспериментальную установку. В компьютерном эксперименте обеспечен полный контроль за всеми параметрами системы, компьютерный эксперимент дешев и безопасен, с помощью компьютера удается ставить "принципиально невозможные" эксперименты (геологические процессы, космология, экологические катастрофы и т.д.).

Список используемых источников

1) Тупик Н.В. Компьютерное моделирование: учебное пособие Тупик Н.В.— Электрон. текстовые данные.— Саратов: Вузовское образование, 2013.— 230 c.— Режим доступа: http://www.iprbookshop.ru/13016.— ЭБС «IPRbooks»

2) Бирюков Б. В., Гастеев Ю. А., Геллер Е. С. Моделирование. - М.: БСЭ

3) Советов Б.Я., Яковлев С.А. Моделирование систем: Учебник для вузов

4) Воинов А. А. Имитационное моделирование в экологии: озеро, пруды, водохранилища /Математическое моделирование. Методы описания и исследования сложных систем. М.: Наук

5) Математическое моделирование. Методы описания и исследования сложных систем. М.: Наука

Ведомость работы