МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИИСКОЙ ФЕДЕРАЦИИ
Федеральное государственное бюджетное образовательное учреждение
высшего образования
«Тверской государственный технический университет»
ИДПО ЗО
КОНТРОЛЬНАЯ РАБОТА
Тема: СИНТЕЗ РЕГУЛЯТОРОВ В САР МЕТОДОМ
РАСШИРЕННЫХ ЧАСТОТНЫХ ХАРАКТЕРИСТИК (РЧХ)
Тверь 2016
Наибольшее применение при автоматизации технологических процессов находят одноконтурные САР с типовыми линейными законами регулирования [4]. Структурная схема такой САР показана на рис. 6.1, где 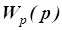 – передаточная функция регулятора;
– передаточная функция регулятора; 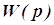 – передаточная функция объекта регулирования.
– передаточная функция объекта регулирования.
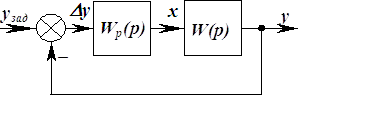
Рис. 6.1. Структурная схема САР с типовым линейным регулятором
Классификация регуляторов по закону регулирования
Под законом регулирования понимают уравнение динамики регулятора. Известны пять типовых законов регулирования: пропорциональный (П), интегральный (И), пропорционально-интегральный (ПИ), пропорционально-дифференциальный (ПД) и пропорционально-интегрально-дифференциальный (ПИД).
Метод расширенных частотных характеристик
Метод расширенных частотных характеристик разработан Е.Г. Дудниковым для расчета настроек регуляторов САР с типовыми линейными законами регулирования. Требования к показателям качества противоречивы. Например, уменьшение динамической ошибки достигается за счёт увеличения колебательности и длительности переходных процессов. Наоборот, процессы с малым временем регулирования удаётся получить за счёт увеличения динамической ошибки. Поэтому относительно желаемых значений показателей качества в замкнутой САР приходится принимать компромиссное решение. В тех случаях, когда ставится задача выбора настроек регулятора, минимизирующих какой-либо показатель качества, соответствующий переходный процесс, а также значения настроек регулятора называются оптимальными в смысле указанного критерия.
Расчет настроек регуляторов методом РЧХ
Для получения уравнения ЛРЗ необходимо записать условие нахождения системы на границе заданной колебательности. Согласно критерию Найквиста для РЧХ условием заданной колебательности в замкнутой САР является прохождение расширенной АФХ разомкнутой системы через точку 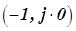 , т.е.
, т.е.
 .
.
Расширенными частотными характеристиками называются выражения для передаточной функции, в которых переменная 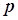 заменяется уравнением границы заданной колебательности.
заменяется уравнением границы заданной колебательности.
Линией равного затухания называется геометрическое место точек в плоскости настроечных параметров регулятора, для которых величина степени колебательности  постоянна. ЛРЗ изображают в плоскости двух настроечных параметров: для ПИ-регулятора в плоскости
постоянна. ЛРЗ изображают в плоскости двух настроечных параметров: для ПИ-регулятора в плоскости  , для ПД-регулятора в плоскости
, для ПД-регулятора в плоскости 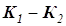 . Настройкам П- и И-регуляторов соответствуют точки пересечения ЛРЗ, построенной в плоскости
. Настройкам П- и И-регуляторов соответствуют точки пересечения ЛРЗ, построенной в плоскости  с координатными осями. При
с координатными осями. При 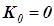 получаем настройку П-регулятора
получаем настройку П-регулятора 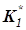 , а при
, а при 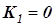 – настройку И-регулятора
– настройку И-регулятора 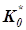
Для получения уравнения ЛРЗ необходимо записать условие нахождения системы на границе заданной колебательности. Согласно критерию Найквиста для РЧХ условием заданной колебательности в замкнутой САР является прохождение расширенной АФХ разомкнутой системы через точку 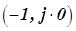 , т.е.
, т.е.
 .
.
Уравнения ЛРЗ для системы с ПИД – регулятором в виде:

Подставляя в систему  , получим уравнения ЛРЗ для системы c ПИ – регулятором:
, получим уравнения ЛРЗ для системы c ПИ – регулятором:
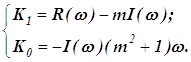
Для ПД-регулятора интегральная составляющая 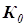 равна нулю. Подставляя в
равна нулю. Подставляя в 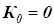 , получим:
, получим:

откуда уравнения ЛРЗ для системы c ПД – регулятором имеют вид:
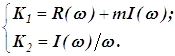
clear
close all
clc
num=[3];
den=[1 4 2 ];
W=tf(num,den)
m=0.5% степень колебательности
tz=5% желаемое время регулирования
sigz=20;% желаемое перегулирование
[y,t]=step(W);
figure(1)
plot(t,y,"g","LineWidth",1)
grid on
w=[0:0.1:10];% диапазон частот
Wreg=-polyval(den,(j-m)*w)./polyval(num,(j-m)*w);% РЧХ регулятора
R=real(Wreg);% действительная часть РЧХ регулятора
I=imag(Wreg);% мнимая часть РЧХ регулятора
K2=[0 0.5 1.5 2 3]
dif=length(K2)% размерность массива К2
for i=1:dif
K1=R-m*I+K2(i)*m*w;%
K0=-(m^2+1)*I.*w+K2(i)*(m^2+1)*w.*w;%
kp=0; K1_plus=[]; K0_plus=[]; % положительные настройки
figure(2+i)
sig=[]; tp=[]; J=[];
for j=1:length(K1)
if (K1(j)>0) && (K0(j)>0) && (K0(j)*K2(i)/K1(j)^2<=0.5)
kp=kp+1;
K1_plus(kp)=K1(j);
K0_plus(kp)=K0(j);
Wr=tf([K2(i) K1_plus(kp) K0_plus(kp)],[1 0]);%
F=feedback(W*Wr,1,-1);
%r=pole(F)
[y1,t1]=step(F);
plot(t1,y1,"b")
grid on
hold on
tp(kp)=t1(end);
sig(kp)=(max(y1)/y1(end)-1)*100;
K1_plus;
K0_plus;
end;
end;
tp
sig
ws=1
wt=1
J=ws*abs(sig-sigz)/sigz+abs(tp-tz)/tz
[Jmin(i),kmin(i)]=min(J)
K1_opt(i)=K1_plus(kmin(i))
K0_opt(i)=K0_plus(kmin(i))
Wopt=tf([K2(i) K1_opt(i) K0_opt(i)],[1 0]);
Fopt=feedback(W*Wopt,1,-1);
%r=pole(F)
[y2,t2]=step(Fopt);
plot(t2,y2,"r")
figure(3+dif)
plot(t2,y2,"r")
grid on
hold on
figure(2)
plot(K1_plus,K0_plus,"m")
hold on
plot(K1_plus,K0_plus,"*r")
grid on
hold on
plot(K1_opt(i),K0_opt(i),"^k")
xlabel("K1");ylabel("K0");title("ЛРЗ K0=f(K1)")
end
Jmin
[Jbest,kbest]=min(Jmin)
Wr=tf([K2(kbest) K1_opt(kbest) K0_opt(kbest)],[1 0]);
F=feedback(W*Wr,1,-1);
[y1,t1]=step(F);
figure(3 +dif)
plot(t1,y1,"b")
grid on
hold on
Transfer function:
3
-------------
s^2 + 4 s + 2
m = 0.5000 степень колебательности
tz = 5 желаемое время регулирования
K2 = 0 0.5000 1.5000 2.0000 3.0000
dif =5
tp =
Columns 1 through 13
19.3048 16.0873 13.7891 11.7056 15.4557 13.7645 12.1880 7.7298 10.2640 6.5500 8.6673 8.0326 7.5811
Columns 14 through 26
7.2361 7.0568 6.9403 6.2950 6.0089 6.2950 6.0327 5.7914 5.5687 5.3624 5.1709 4.9926 4.8262
Columns 27 through 35
4.6705 4.5246 4.3874 2.8389 2.7578 6.6739 6.4935 16.8144 23.4853
sig =
Columns 1 through 13
19.4573 19.8246 20.6441 21.5902 23.9968 25.2339 26.4786 26.0183 28.6746 27.8497 30.5213 31.2778 31.8398
Columns 14 through 26
32.2752 32.4955 32.5597 32.7651 32.6429 32.1792 31.8401 31.3428 30.6877 29.9152 29.0296 27.9857 26.7892
Columns 27 through 35
25.4514 24.0398 22.5441 19.9157 18.7816 17.6681 16.2702 13.5190 11.9446
ws =1
wt =1
J =
Columns 1 through 13
2.8881 2.2262 1.7900 1.4206 2.2910 2.0146 1.7615 0.8469 1.4865 0.7025 1.2595 1.1704 1.1082
Columns 14 through 26
1.0610 1.0361 1.0160 0.8973 0.8339 0.8680 0.7986 0.7254 0.6481 0.5682 0.4857 0.4008 0.3742
Columns 27 through 35
0.3385 0.2971 0.2497 0.4364 0.5094 0.4514 0.4852 2.6869 4.0998
Jmin = 0.2497
kmin = 29
K1_opt = 4.6408
K0_opt = 3.1762
tp =
Columns 1 through 13
7.5675 7.1488 7.3603 7.1940 6.4128 7.0764 5.7299 6.7877 5.8665 5.6140 5.3736 5.1438 4.9236
Columns 14 through 26
4.7122 4.5092 4.3144 4.1278 4.3714 4.1837 4.0059 4.2424 4.0688 3.9069 3.7565 3.9619 3.8210
Columns 27 through 39
3.6910 3.5710 3.7359 3.6249 3.5219 4.7367 2.0602 2.0085 2.4286 2.3720 11.6946 6.1675 11.6461
sig =
Columns 1 through 13
27.7549 28.5462 28.8696 29.3274 30.4857 30.0252 31.6294 30.8764 31.8468 32.2751 32.6268 32.8814 33.0882
Columns 14 through 26
33.2670 33.2914 33.2443 33.1177 32.5991 32.4481 32.1220 31.4837 31.0530 30.6130 30.0306 29.2473 28.5155
Columns 27 through 39
27.7806 26.9111 25.9454 24.9600 23.8782 22.9228 20.3859 19.4522 19.3914 18.5899 16.6980 16.2998 15.2306
ws = 1
wt = 1
J =
Columns 1 through 13
0.9012 0.8571 0.9155 0.9052 0.8069 0.9165 0.7275 0.9014 0.7656 0.7366 0.7061 0.6728 0.6697
Columns 14 through 26
0.7209 0.7627 0.7993 0.8303 0.7557 0.7857 0.8049 0.7257 0.7389 0.7493 0.7502 0.6700 0.6616
Columns 27 through 39
0.6508 0.6314 0.5501 0.5230 0.4895 0.1988 0.6073 0.6257 0.5447 0.5961 1.5040 0.4185 1.5677
Jmin = 0.2497 0.1988
kmin = 29 32
K1_opt =
4.6408 8.6158
K0_opt =
3.1762 7.3633
tp =
Columns 1 through 13
4.0487 3.9775 4.0117 3.9250 3.9586 3.9971 3.0164 2.7823 3.1048 2.8132 2.6624 2.8042 2.7492
Columns 14 through 26
2.6501 2.5539 2.4609 2.6246 2.5298 2.4395 2.6016 2.5125 1.7735 1.7165 1.6634 1.6141 1.5684
Columns 27 through 39
1.5260 1.4867 1.4501 1.4161 1.3844 1.3547 1.3269 1.6118 1.5812 1.5524 1.5251 1.3545 1.3322
Columns 40 through 41
1.3110 1.2907
sig =
Columns 1 through 13
31.6155 31.7560 32.0263 32.0709 32.2669 32.4025 33.0393 33.5399 32.3557 32.9887 33.0524 32.4162 32.2867
Columns 14 through 26
32.2232 31.9828 31.7709 31.1931 30.9978 30.6619 30.1145 29.7624 28.1139 27.6470 27.2053 26.7056 26.2235
Columns 27 through 39
25.6535 25.0991 24.4868 23.8181 23.1845 22.5208 21.8469 21.7952 21.1200 20.4850 19.9162 19.1025 18.7857
Columns 40 through 41
18.6182 18.6332
ws = 1
wt = 1
J =
Columns 1 through 13
0.7710 0.7923 0.7990 0.8185 0.8216 0.8207 1.0487 1.1205 0.9968 1.0868 1.1201 1.0600 1.0645
Columns 14 through 26
1.0811 1.0884 1.0964 1.0347 1.0439 1.0452 0.9854 0.9856 1.0510 1.0391 1.0276 1.0124 0.9975
Columns 27 through 39
0.9775 0.9576 0.9343 0.9077 0.8823 0.8551 0.8270 0.7674 0.7398 0.7138 0.6992 0.7740 0.7943
Columns 40 through 41
0.8069 0.8102
Jmin = 0.2497 0.1988 0.6992
kmin = 29 32 37
K1_opt = 4.6408 8.6158 21.3333
K0_opt = 3.1762 7.3633 13.3333
tp =
Columns 1 through 13
3.2236 3.1827 3.2310 3.2318 3.2541 2.3739 2.4456 2.4019 2.5022 2.4516 2.2086 2.5113 2.1627
Columns 14 through 26
2.1912 2.1178 2.2654 2.1896 2.1169 2.2630 2.1901 2.3232 1.5014 1.4569 1.4153 1.3765 1.3404
Columns 27 through 39
1.3067 1.2753 1.2461 1.2188 1.1933 1.4490 1.4211 1.3949 1.3702 1.3468 1.3246 1.3036 1.2836
Columns 40 through 43
1.1425 1.1260 1.1103 1.0952
sig =
Columns 1 through 13
31.9391 31.9997 32.1940 32.2754 32.3518 33.5678 33.0589 33.0022 32.3741 32.3487 32.7519 31.7431 32.3022
Columns 14 through 26
31.9478 31.7682 31.1862 31.0434 30.7702 30.2749 29.9803 29.5534 28.0865 27.7576 27.3553 27.0124 26.6037
Columns 27 through 39
26.1847 25.7455 25.2404 24.7475 24.2224 24.3071 23.6851 23.0840 22.4755 21.8738 21.2943 20.7658 20.3110
Columns 40 through 43
19.6258 19.3587 19.1980 19.1647
ws =1
wt =1
J =
Columns 1 through 13
0.9522 0.9635 0.9635 0.9674 0.9668 1.2036 1.1638 1.1697 1.1183 1.1271 1.1959 1.0849 1.1826
Columns 14 through 26
1.1591 1.1648 1.1062 1.1142 1.1151 1.0611 1.0610 1.0130 1.1040 1.0965 1.0847 1.0753 1.0621
Columns 27 through 39
1.0479 1.0322 1.0128 0.9936 0.9725 0.9256 0.9000 0.8752 0.8497 0.8243 0.7998 0.7776 0.7588
Columns 40 through 43
0.7902 0.8069 0.8180 0.8227
Jmin = 0.2497 0.1988 0.6992 0.7588
kmin = 29 32 37 39
K1_opt = 4.6408 8.6158 21.3333 29.0208
K0_opt = 3.1762 7.3633 13.3333 18.8021
tp =
Columns 1 through 13
2.3954 1.7703 2.3975 1.7485 1.7793 1.7415 1.7905 1.6548 1.8005 1.6473 1.7032 1.6271 1.6724
Columns 14 through 18
1.7224 1.7268 1.6772 1.6293 1.7499
sig =
Columns 1 through 13
32.3495 34.0259 32.3532 33.7043 33.3803 33.3239 32.8907 33.0568 32.4250 32.6352 32.2937 32.1801 31.8807
Columns 14 through 18
31.5271 31.2556 31.1137 30.9057 30.4700
ws =1
wt =1
J =
Columns 1 through 13
1.1384 1.3472 1.1382 1.3355 1.3132 1.3179 1.2864 1.3219 1.2612 1.3023 1.2740 1.2836 1.2596
Columns 14 through 18
1.2319 1.2174 1.2202 1.2194 1.1735
Jmin = 0.2497 0.1988 0.6992 0.7588 1.1382
kmin = 29 32 37 39 3
K1_opt = 4.6408 8.6158 21.3333 29.0208 29.4375
K0_opt = 3.1762 7.3633 13.3333 18.8021 135.4688
Jmin = 0.2497 0.1988 0.6992 0.7588 1.1382
Jbest =0.1988
kbest = 2
Вывод:
Из рис. 1 видно, что при синтезе САР методом РЧХ получена система с заданной степенью колебательности m=0.4, а отклонения от желаемых перерегулирования sig 15 % и времени переходного процесса tz=5 c очень малы.
Результаты работы программы для объекта регулирования с колебательной передаточной функцией ПИД-регулятора и тех же желаемых характеристик качества приведены на рис. 2.
Семейство ЛРЗ для приведенных значений 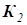 показано на рис. 3 - 7 На каждой кривой по
показано на рис. 3 - 7 На каждой кривой по 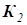 находятся наилучшие по критерию J настройки
находятся наилучшие по критерию J настройки 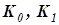 , из которых затем определяются оптимальные.
, из которых затем определяются оптимальные.
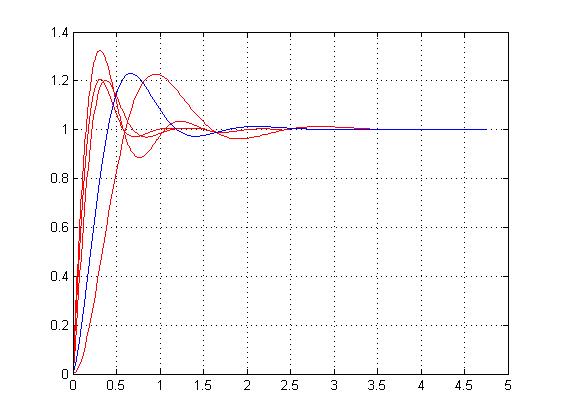
На рис. 7 показаны наилучшие по критерию J переходные процессы для каждой из линий равного затухания и оптимальный процесс, удовлетворяющий требуемым характеристикам качества.
График (1) переходного процесса замкнутой системы
Y(t)
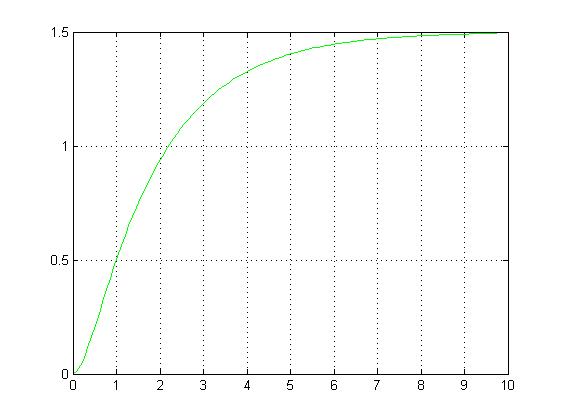 t
t
График(3) Семейство переходных процессов при К2=1
Y(t)
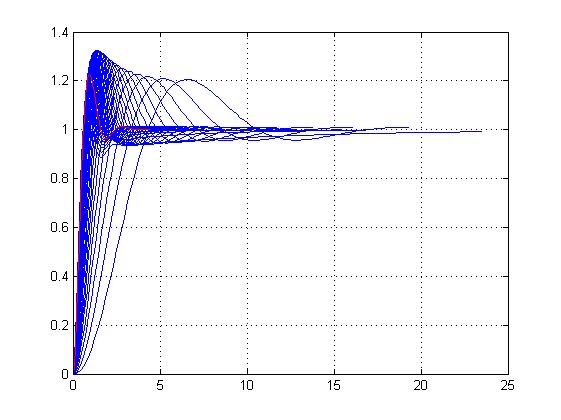
t
График (5) Семейство переходных процессов при К2=2
Y(t)

t
График (4) Семейство переходных процессов при
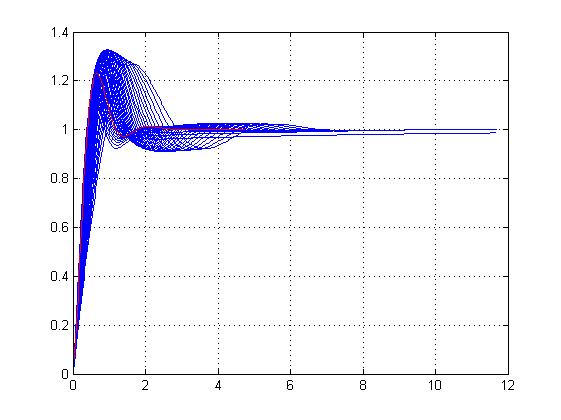
График (6) Семейство переходных процессов при

График (7) Семейство переходных процессов при К2=3
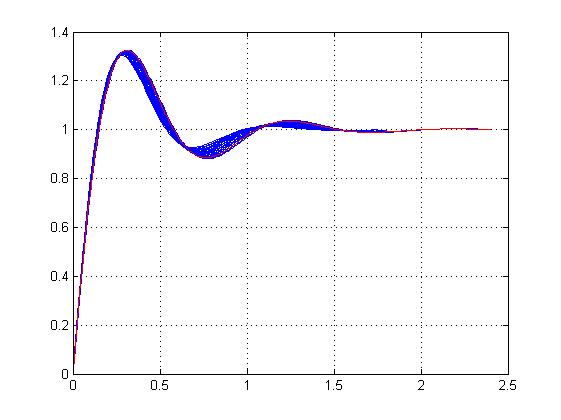
График (2) Семейство ЛРЗ для ПИД-регулятора

График (8) Семейство оптимальных переходных процессов лучший выделен синим цветом
y(t)
t














 (zip - application/zip)
(zip - application/zip)










