Текст:

Дніпропетровський національний університет імені Олеся Гончара

Кафедра радіоелектроніки

РЕФЕРАТ

з курсу: «ФІЗИКА ТВЕРДОГО ТІЛА»

на тему: «Що таке квазікристали?»

Студента IІ курсу групи КМ-14

напряму підготовки

«Мікро- та наноелектроніка»

Балабухи В. О.

Керівник к. ф.-м. н., доц.

Буланий М. Ф.

Національна шкала _________________

Кількість балів: _____Оцінка: ECTS___

м. Дніпропетровськ – 2016 рік

Оглавление

ВСТУП.. 3

1. Структура кристалів. 3

1.1 Поняття трансляції. 5

1.2 Типи кристалічних решіток. 7

2.Особенности структури квазікрісталлові властивостей. 8

2.1 Історія відкриття квазікристалів. 8

2.2 Особливості структури. 10

2.3 Властивості квазікристалів. 16

2.4.Прімененіеквазікрісталлов. 17

Висновок. 19

СПИСОК ВИКОРИСТАНОЇ ЛІТЕРАТУРИ.. 20

ВСТУП

Створення нових багатофункціональних матеріалів з незвичайними властивостями є завданням і характерною рисою сучасної науки і техніки. Кінець ХХ-століття був ознаменований відкриттям високотемпературних провідників, фулерон, нанотрубок і квазікристалів. Квазікристали (КК) є новий клас матеріалів, які характеризуються далеким порядком в розташуванні атомів і симетрією, яка заборонена класичної кристалографії кристалів. Відкриття квазікристалів поставило принципові питання про організацію, стабільності і властивостей конденсованого стану матеріалів. Дослідження квазікристалів істотно розвинули уявлення про кластерну періодичну структуру, дали суттєвий поштовх розвитку n-мірної кристалографії, фізики і хімії твердого тіла, виявили новий набір фізико-хімічних властивостей. Дослідження особливостей структури і властивостей дає нові можливості для розвитку нових технологій, які змінюють сучасний світ. За відкриття квазікристалів було присуджено Нобелівську премію в галузі хімії.

1. Структура кристалів

Геометрично правильна зовнішня форма кристалів, що утворюються в природних або лабораторних умовах, наштовхнула вчених ще в сімнадцятому столітті на думку, що кристали утворюються за допомогою регулярного повторення в просторі одного і того ж структурного елементу, так би мовити, цеглинки (рис. 1.1) . При зростанні кристала в ідеальних умовах форма його протягом всього зростання залишається незмінною, як якби до зростаючого кристалу безперервно приєднувалися б елементарні цеглинки. Зараз ми знаємо, що такими елементарними цеглинками є атоми або групи атомів. Кристали складаються з атомних рядів, періодично повторюваних в просторі і утворюють кристалічну решітку.

У вісімнадцятому столітті мінералогами було зроблено важливе відкриття. Виявилося, що індекси (знайдені певним способом, описаним нижче), що визначають положення в про-просторі будь-якої грані кристала, суть цілі числа. Гаюї [1-2] показав, що це можна пояснити розташуванням ідентичних частинок в ряди, періодично повторювані в просторі. У 1824 р Зібер [3] з Фрайбурга припустив, що елементарні складові кристалів ( «цеглинки», атоми) є маленькими сферами. Він запропонував емпіричний закон міжатомной сили з урахуванням як сил тяжіння, так і сил відштовхування між атомами, що було необхідно для того, щоб кристалічна решітка була стабільним рівноважним станом системи ідентичних атомів.

Мабуть, найбільш важливою датою в історії фізики твердого тіла є 8 червня 1912 У цей день в Баварської Академії наук в Мюнхені слухався доповідь «Інтерференціярентгеновскіх променів». У першій частині доповіді Лауе виступив з викладом елементарної теорії дифракції рентгенівських променів на періодичному атомному ряду. У другій частині доповіді Фрідріх і Кніппінг повідомили про перших експериментальних спостереженнях дифракції рентгенівських променів в кристалах.

Цією роботою було показано, що рентгенівські промені є хвилями, так як вони здатні дифрагувати. Робота незаперечно довела також, що кристали складаються з пе-періодичних рядів атомів. З цього дня почалася та фізика твердого тіла, який ми знаємо її сьогодні. У роки, непосред¬ственно наступні за 1912 роком, у фізиці твердого тіла було зроблено багато важливих піонерських робіт. Першими кристалічними структурами, визначеними У. Л. Брегг в 1913 р за допомогою рентгенівського дифракційного аналізу, були структури кристалів KCl, NaCl, КВг і Кl.

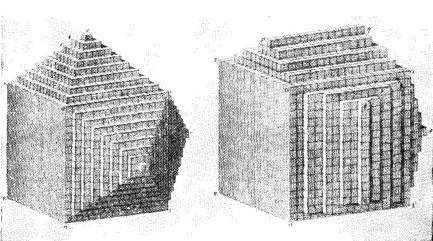
Рис. 1.1. Связь внешней формы кристаллов с формой элементарных структурных элементов. Структурные элементы одинаковы в случаях, изображенных слеза и справа, но развитие получают разные грани.

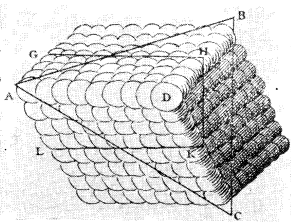
Рис 1.2 Модель кальциту(СаСО₃) по Гюйгенсу.

1.1 Поняття трансляції.

Визначимо ідеальний кристал як тіло, що складаються з атомів, розташованих в просторової решітці так, що можна вести три вектора основних трансляцій a, b, c, що володіють наступною властивістю. При розгляді цієї атомної решітки з довільної точки r решітка має той же вигляд, що і при розгляді з точки r^¢:

r^¢=r+n₁a+n₂b+n₃c, (1.1)

де n₁, n₂, n_{3 - Довільні цілі числа
(рис.1.3) Основні вектори трансляцій іноді позначаються}a₁, a₂, a₃.

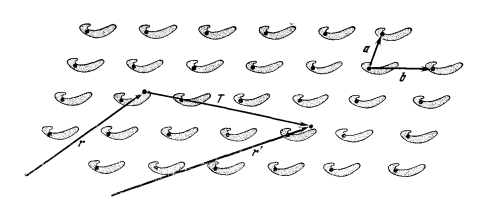
Рис. 1.3. Частина кристала (в двомірному зображенні), побудованого з гіпотетичних білкових молекул. (Ми обрали білкову молекулу тому, що ця молекула, ймовірно, не має своєї власної симетрії.) Атомне розташування в кристалі має однаковий вигляд як при розгляді з точки r", так і при розгляді з точки r.через це вектор Т, що зв"язує r’ і r можна виразити як (ціле) кратне векторів а і Ь. Наприклад, на цьому малюнку Т = -а + 3b. Вектори а і b є векторами примітивних трансляцій двомірної решітки.

сукупність точок r, обумовлена співвідношенням (1.1) при різних значеннях чисел n₁,n₂, п₃визначає кристалічну решітку, яка була регулярне періодичне розташування точок в просторі. Кристалічна решітка є математичною абстракцією: кристалічна структура утворюється лише тоді, коли з кожною точкою решітки пов"язаний (однаковим чином) базис. Таким чином, логічно записати, що

решітка + базис = кристалічна структура.

Кристалічна решітка називається примітивною, а вектори а, b, с - векторами примітивних трансляцій, якщо дві будь-які точки r і r ",при спостереженні з яких атомне розташування має однаковий вигляд, завжди задовольняють співвідношенню (1.1) при відповідному виборі цілих чисел n _1, n _2, п _3. Вектори примітивних трансляцій ми будемо часто вибирати в якості ортів кристалографічних осей координат,хоч на ряду з цим будуть використовуватися і інші (не примітивні) трійки векторів, коли вони більш зручні і користуватися ними простіше. Вектори а, b, с, обрані в якості ортов кристалографічних осей, утворюють три суміжних) кута елементарного паралелепіпеда.Якщо точки решітки знаходяться тільки в кутах паралелепіпеда, то такий паралелепіпед називається примітивним. Операцію переміщення кристала як цілого паралельно самому собі, що описується вектором

Т = n ₁ а + п ₂ b + n ₃ з = n ₁ а ₁ + п ₂ а ₂ + n ₃ а _2,

будемо називати трансляцією. Вектор трансляції кристалічної решітки пов"язує будь-які дві точки решітки.

1.2 Типи кристалічних решіток

Кристалічні решітки можуть бути приведені в самосовмещеніе не тільки в результаті трансляційних перетворень, а й в результаті різних точкових операцій симетрії. Типовою операцією симетрії є обертання навколо осі, що проходить через якусь точку решітки. Існують решітки мають осі обертання першого, другого, третього, четвертого і шостого порядку, які відповідають поворотам на кути 2π, 2π / 2, 2π / 3, 2π / 4, і 2π / 6.

Осі обертання інакше називаються поворотними осями. Вони позначаються цифрами 1, 2, 3, 4 і 6. Раніше вважалося що не існує кристалічних решіток, що мають поворотні осі п"ятого та сьомого порядку [4] .Молекула сама по собі може мати поворотну вісь симетрії будь-якого порядку, на відміну від нескінченного періодичного кристалічної решітки. Кристал може складатися з молекул, кожна з яких має поворотну вісь п"ятого порядку, але кристалічна решітка не матиме цю вісь. На рис. 1.4 показано, що відбувається якщо спробувати створити періодичну решітку з віссю п"ятого порядку: п"ятикутники не підходять один до одного впритул.

Рис. 1.4 У кристалічній решітці не може існувати вісь симетрії п"ятого порядку: неможливо за допомогою п"ятикутників заповнити весь простір решітки без проміжків.

Таким чином, видно, що не можна поєднувати п"ятикратну точкову симетрію з необхідною трансляційній симетрією. На рис.1.5 показано, що в кристалах не може бути поворотною осі сьомого порядку

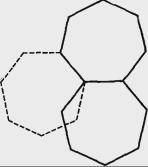
Рис. 1.5. Малюнок Кеплера ( «Harmo-nicemundi», 1619), з якого видно, що в кристалічній решітці не може існувати вісь симетрії сьомого порядку [5].

2.Особенности структури квазікрісталлові властивостей

2.1 Історія відкриття квазікристалів

12 листопада 1984 року в невеликій статті, опублікованій в авторітетномжурнале «PhysicalReviewLetters», було пред"явлено експеріментальний доказ існування металевого сплаву з виключними властивостями (Шехтман і ін., 1984). При дослідженні методами електронної дифракціі цей сплав, мабуть, проявляє себе як кристал. Його дифракційна картина складена з яскравих і регулярно розташованих точок, зовсім як у кристала. Однак картина ця також характеризується наявністю «ікосаедрическої» симетрії, строго забороненої в крісталі з геометричних міркувань. Статтю в 1984 р написали четверо дослідників: автор відкриття Д. Шехтман, Я. Блех з Технічного інстітутав Хайфі (Ізраїль), Дж. У. Кан з Національного бюро стандартів (США) і я - співробітник Центру досліджень по хімії і металургії національного наукового центру (Франція).

Ми всі були переконані, що це дивне відкриття викличе величезний інтерес в галузі фізики твердого тіла і в кристалографії. І не були розчаровані: пішло понад двохсот наукових публікацій, присвячених цим новим речовинам, званим сьогодні «квазікристалів». Через кілька місяців з"явилася на світло струнка теоретична модель квазікристалів. У ній був використаний математичний апарат, створений для опису чарівних неперіодичних структур, прототипами яких були плитки Пенроуза. Менш ніж за рік було відкрито багато інших сплавів і продемонстровані нові типи симетрії. Їх було так багато, що квазікристалічний станів виявився набагато поширеним, ніж ми могли собі уявити.

Поняття квазікристала представляє фундаментальний інтерес, тому що воно узагальнює і завершує визначення кристала. Теорія, заснована на цьому понятті, замінює одвічну ідею про «структурну одиницю, повторювану в просторі строго періодичним чином» ключовим понятіемдальнего порядку. Це поняття призвело до розширення кристалографії, знову відкриті багатства якої ми тільки починаємо вивчати. Його значення в світі мінералів можна поставити в один ряд з додаванням понятіяірраціональних чисел до раціональних в математиці.

Що являє собою квазікристал? Які його властивості і як

можна їх описати? На багато з цих питань зараз можна дати відповіді, грунтуючись на добре перевірених фактах. [6]

2.2 Особливості структури

З точки зору структури квазікристалів мають проміжне положення між кристалами і аморфними тілами. Цей новий клас матеріалів відрізняється від крісталлво тим, що крім осей 2, 3, 4, 6-го порядків присутні також осі 5, 7, 8, 10-го і інших порядків, які заборонені класичної кристалографії. Дифракційна картина, отримана від квазікристалів, являє собою набір гострих інтенсивних відбитків просторі закономірно пов"язане співвідношенням, які включають ірраціональне число τ = 1.618034 ..., «золоте число», τ = 2cos 36˚.

Від аморфних тіл квазікрісталл и відрізняються наявністю далекого порядку в розташуванні і атомів [7], але при цьому на малих відстанях, в першій координатної сфері більшу частину складають атоми в ікосаедріческої координації, як в аморфних тілах.

З погляду квазірешіток, ікосаедричні квазікристалли класифікуються на три типи, а саме, P-тип (примітивна), F-тип (ГЦК) і I-тип (ОЦК) відповідно до шестімерной решітки Браве в методі проекції. Ікосаедричні квазірешітки однозначно описуються за допомогою шестімерной (6D) решітки. Для зручності 6D- простір розкладається на тримірній (3D) ║фізичні (паралельний) простір і додатковий (3D)_,названий перпендикулярним. В 6D-просторі зворотня решітка періодична.Неперіодичних чергування дифракційним максимумів, наприклад ікосаедрічность, обумовлена ірраціональним перетином простору. Прикладом зазначеного служить двовимірне наближення, показане на малюнку 2.1.

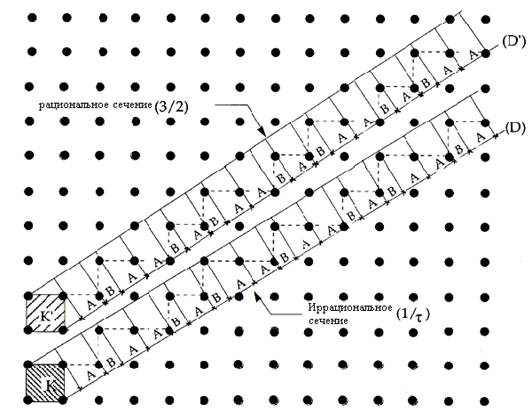
Рис. 2.1-Побудова одновимірного квазікристала методом перетинів і проекцій з двомерной періодичної структури.

Важливою проблемою у фізиці кристалів є уявлення про їх атомну структуру. Її прийнято описувати за допомогою математичної теорії заміщення. Заміщення - це покриття всієї площі або заповнення всього простору без розривів фігурами, що не перекриваються. Для опису структури квазікристалів на сьогодні використовують в основному дві моделі, два підходи. Згідно з першою, так званої «моделі укладання», «модель заміщення», двомерное простір без розривів заповнюється плитками (ромбами) Пенроуза, а простір заповнюється двома ромбоедрі [1,8]

У своїй простій формі плитка Пенроуза - це набір ромбоподобних фігур двох типів: одні з внутрішнім кутом 36º (тонкі) та інші - 72º (товсті ромби) [9]. У нескінченній мозайці Пенроуза співвідношення числа «товстих» ромбів до числа «тонких» точно дорівнює величині золотого перетину, і оскільки це число ірраціональне, в цій мозаїці можна відокремити елементарну середину, яка мала б число ромбів кожного типу. Паркет Пенроуза не є періодичним заміщенням, оскільки не переходить в себе ні за яких зрушення. Однак в цьому існує певний порядок, оскільки будь-яка кінцева частка цього заміщення зустрічається в усьому заміщення нескінченну кількість разів.

На рис. 2.2 видно, що це заміщення має вісь п"ятого порядку, тобто переходить в себе при повороті на кут 72º навколо десятої точки [10].При певних величинах кутів при вершинах виходить ікосаедрична безперервна структура.

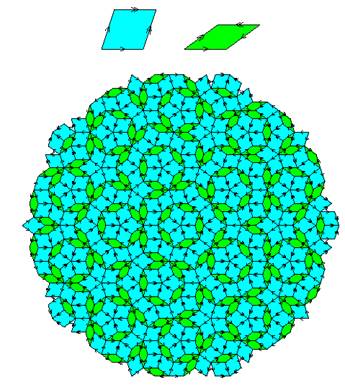
Рис. 2.2 - Центральний фрагмент аперіодичне плоского укладання Пенроуза [11]

У моделі «кластерінга» структура квазікристала представляється побудовою з однакових осередків. Для двомірного випадку ними десятикутник Гумбельта (рис. 2.3), при тому, що окремі автори пропонують ці Десятикутники Гумбельта як двомірну елементарну комірку квазікристала. У 3D-просторі використовують ромбічний триаконтаедр.

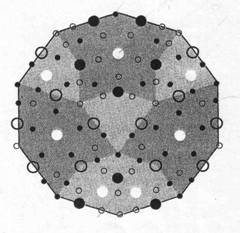
Рис. 2.3 - декорування модель десятіугольніка Гумбельта

Підхід до опису структури аналогічнго укладання Пенроуза тільки в трьохмірному варіанті. Шесть Пенроузовскіх ромбів з довгою діагоналюутворюють два ромбіних шестігранних-паралелепіпедів – сплющенний або витянутий. Два з кожного типу шестігранників ствоюють ромбічний додекаедр. Цей додекаедр можетзаполнятьпростор, так як різні внутрішні кути шестигранників, комбінуясь, когут утворилося замкнені вершини.

Ще по три з кожного типу шестигранників упаковуються навколо ромбічного додекаедра і утворюють тромбічний ікосаедр, навколо якого ще пя’ть з кожних шестигранників пакуються і утворюють ромбічний тріакотаедр. Два ромбичних шестикутника аналогічні двом елементам укладання Пенроуза, а ромбічний троіакотаедр - Десятіугольнік, освіченій з елементів Пенроуза. Десятіугольнік, утворені шляхом забудови Пенроуза, виявляються більшими, ніж десятіугольнік відповідного квазікристала, тобто можна чекати аналогічного співвідношення в будь-якому тривимірному аналогу [8]

Окремі автори пропонують дивитися на ці Десятіугольнік як двомірний елементарних центр квазікристала, а ромбические тріаконтаедри - як тривимірний. З"єднання тріаконтаедров в тривимірну структуру проводиться не в стик, як у кристалів, а з накладенням. Існує три способи накладання, представлені на малюнку 2.4.

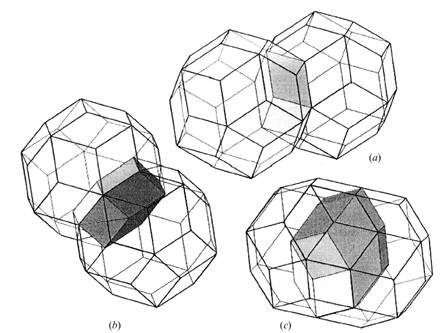
Рис. 2.4 - Три способи об"єднання тріаконтаедров в тривимірну квазікристалічної структуру [12]

З основних критеріїв та формування стабільних ікосаедрічних квазікристалів, можна виділити наступні [1,8]:

1. Квазікристалів утворюються тільки в металевих бінарних _A m B n або потрійних (А, С) _{m B n} системах;

2. Співвідношення розмірів атомів компонентів не є довільним, а має становити _r B / _r A ≈ або _r B / _{A _З> ≈ 1,225, що «Ріднить» i - фазу
з фазами Лавіс;}

3. Компоненти і їх концентрація підбираються так, що електронна атомна концентрація е / аm становила 1,75 або 2,0 .., 2,1. Даний факт робить квазикристалл родственним і електронними фазами Юм-Розера.

Встановлено, що всі QСs з точки зору атомної конфігурації є кластерними матеріалами. Їх структура побудована з атомних кластерів, які неперіодичних повторюються в просторі. Ці кластери влаштовані таким чином, що кожен атом одного сорту оточений Ікосаедр, або додекаедрів з атомів іншого сорту [13] Розрізняють три види кластерів: Маккея (54 атома), Бергмана (44-45) і Тсая (об"єднує в собі два перших) .Ізображеніе всіх трьох оболонок кластером Маккея і Бергмана представлено на малюнку 2.5. Як видно з малюнка атоми розташовані в кластерах так, що б дотримувалася ікосаедрічеськая симетрія. Існування кристалів-апроксімантов, тобто фаз структура яких включає в себе два типи кластерів, і які розташовуються в періодичному порядку, підтверджує правильність структурної ідентифікації квазікристалів [14,15]. Згідно рис. 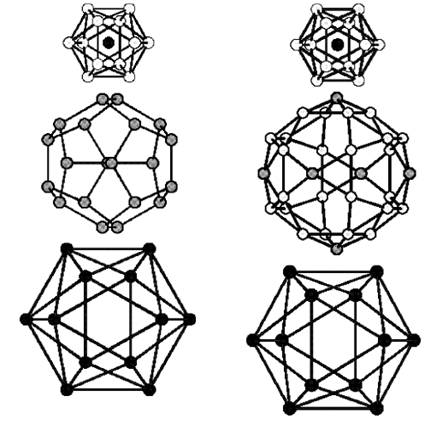2.6 все стабільні QCs збираються в дві області в залежності від координат е / аm і a / , де a _q - параметр квазікрісталлічності і < d> - середній діаметр атома структури. Параметр квазікрісталлічності вводітся для кількісної характеристики структури за аналогією з періодом решітки в кристалах. Він розраховується як a _q = a _6D / √2 де a _6D - параметр кубічних шестімерной гіпер-решіток. У першому наближенні одно довжині боку ромба в моделі побудови Пенроуза

Рис. 2.5 - Структура кластерів квазікрісталів і косаедричного типу Бергмана (1) і Маккея (2) [6].

Рис. 2.6 - Зв"язок між електронною густиною на атом і a _q / [16].

2.3 Властивості квазікристалів.

Квазікристалів, як правило, сплави металевих елементів. Але фізичні властивості квазікристалів відрізняються від властивостей інших металевих систем. Електроопір металів збільшується при зростанні температури, концентрації домішок, структурних дефектів. Квазікристалів НЕ ізолятори і не напівпровідники, але на відміну від металів їх електроопір при низьких температурах аномально велике, зменшується з ростом температури і зростає в міру збільшення структурного порядку і відпалу дефектів (тривале нагрівання, що усуває дефекти).

Інша особливість - кінцевий, як у металів, лінійно залежить від температури електронний вклад в питому теплоємність. У порівнянні з металом він занижений, але вказує на наявність вільних носіїв заряду; у діелектриків подібного вкладу в теплоємності немає.
Практично всі квазикристаллические сплави - Діамагнетик. Виняток становлять сплави з марганцем, є парамагнетиками.

Теорія твердого тіла прекрасно пояснює електронні властивості нормальних металів і їх сплавів. Відправним пунктом є періодичність кристалічної структури. Однак теорія ще не в змозі пояснити, чому квазіперіодичності є джерелом специфічного поведінки властивостей. Для відповіді на це питання необхідна велика експериментальна і теоретична інформація про електронну будову (електронному спектрі) квазікристалів.

Цікаві пружні і пластичні властивості квазікристалів. Пружні модулі квазікристалів менше за величиною, ніж модулі близьких за складом кристалічних фаз. За пружним властивостям квазікристалів набагато ближче до аморфним металів, ніж до кристалів. Знижений значення пружних модулів вказує на більш слабке міжатомна взаємодія, і на перший погляд квазікристали повинні легше деформуватися, ніж їх кристалічні аналоги.Однак висока сила опору руху дислокацій (лінійних дефектів, відповідальних за пластичну деформацію) в квазікристалів робить їх менш пластичними і відповідно реальними кандидатами на роль ефективних упрочнителей в сплавах.

2.4.Прімененіеквазікрісталлов

На сьогоднішній день розроблені нові високоміцні алюмінієві сплави, які укріплені нанодисперсному частками квазікристалів, для підвищення температур і технологією їх отримання. Ці сплави, на відміну від існуючих високоміцних алюмінієвих сплавів, які деформуються, і можуть бути застосовані тільки при температурі 110 ^про З, можуть бути застосовані при температурах до 300 ^про З, що дуже необхідно для сучасної авіації.Сплави мають рекордні для алюмінієвих сплавів характеристики жароміцності.

Також розроблена технологія нанесення квазікристалічних покриттів може бути застосовна в різних галузях техніки для створення термічних бар"єрів, захисних покриттів, і покриттів на інструменті, що покращують його властивості. З"ясовано умови та розроблено методику отримання методом ультразвукової ударної обробки високоміцних і зносостійких композитних шарів на поверхні алюмінієвих сплавів за рахунок утворення стабільної квазікристалічної фази системи Al-Cu-Fe, на відміну від сплавів системи Al-Fe-Cr, де зміцнює фазою є метастабільні квазикристаллические частки . Доведено, що такі композиційні шари мають істотно підвищену зносостійкість в порівнянні з немодіфіцированим матеріалом.

Чисельні дослідження показали, що завдяки своїм унікальним властивостям квазикристаллические матеріали можуть бути використані в авіації, автомобілебудуванні, ядерної, термоядерної і водневої енергетики, космічної техніки, приладобудуванні та інших галузях господарства.

Висновок

Можливість практичного застосування квазікристалів визначають наступні властивості: міцність, низький коефіцієнт тертя, низька теплопровідність і незвичайні електропровідні властивості. Сьогодні передбачається кілька областей їх застосування, зокрема створення покриттів і додавання квазікристалічних наночасток в сплави.

Найважливіша область застосування - виробництво покриттів. Це більш перспективно, ніж використання цілісних квазікристалів. Останні досить тендітні, а при використанні покриттів проявляється їх жорсткість. Інший спосіб уникнути проблеми крихкості квазікристалічних матеріалів - використовувати ікосаедріческіеквазікрісталліческіе частки нанометрових розмірів для армування сплавів на основі алюмінію. Зараз такі матеріали комерційно доступні в Японії та Швеції. Їх вже використовують для виготовлення лез і хірургічних інструментів, особливо в очній хірургії. Майбутні перспективи дуже широкі; зокрема, матеріали з такими властивостями потрібні в авіаційній промисловості.

Низька теплопровідність і електропровідність квазікристалів відкриває можливості їх використання для створення термоелектричних матеріалів, конвертують теплову енергію в електричну. Це допоможе утилізувати непридатне тепло, наприклад, в автомобілях.

Незважаючи на надзвичайно цікаві властивості квазікристалів, їх практичне застосування, скоріше, завдання майбутнього. Промислове впровадження гальмує ряд технічних проблем: виробництво значних кількостей квазікристалів - не проста, хоча і можна вирішити завдання, а ціна їх поки надзвичайно висока.

СПИСОК ВИКОРИСТАНОЇ ЛІТЕРАТУРИ

1. Остроушко О. О. Основы аналитической химии / Олександр Олександрович Остроушко. –Єкатеринбург:УФУім. О. М. Горького, 2008.–213с.

2. Остроушко О. О. Кристали / О. О. Остроушко , М.Ю.Сенніков. – Єкатеринбург:УФУім. О. М. Горького, 2005. - 105 с.

3. Арманд Е. Н. Техническая энцикполепидя / Е. Н. Арманд, Н. М. Ельцина, А. А. Знаменский. – Москва: Советская энциклопедия, 1934. – 452 с.