Ряд Фурье. Разложение в ряд Фурье четных и нечетных функций

Министерство образования и науки Российской Федерации

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ

ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

«ОРЕНБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ»

Математический факультет

Кафедра алгебры и математической кибернетики

РЕФЕРАТ

Ряд Фурье. Разложение в ряд Фурье четных и нечетных функций.

ОГУ 220100.62.6012.069 Р

Руководитель

                                                                               Старший преподаватель

                                                                                _____________ Д.У. Шакирова

                                                                               «___»_________
___20__г.

Исполнитель

Студент группы

11САУ(б)ИТ

 _____________ Л.С. Арсланова

 «___»____________20__г.

 

Оренбург 2012

Содержание

1Ряды. Общие понятия…………………………………………………………..…3

2 Ряд Фурье. Общие понятия…………………………………………………….…5

3 Ряды Фурье для четных и нечетных функций……………………………….….7

4 Некоторые замечания разложения четных и нечетных функций  в ряд Фурье.8

5 Примеры разложения некоторых четных и нечетных функци в ряд Фурье….11

Список использованных источников……………………………………………...19

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1 Ряды. Общие понятия.

Рассмотрим числовую последовательность . Выражение

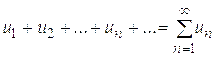                                              (1)

называется (бесконечным) числовым рядом, числа  - членами ряда, 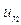 - общим членом ряда, а сумма первых “n” членов  - частичной суммой ряда.

         Ряд называется сходящимся, если существует конечный предел последовательности частичных сумм 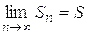, а число S называется суммой ряда.

         Если последовательность не имеет конечного предела, то говорят, что ряд расходится. Однако в случае, когда 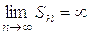, говорят, что ряд имеет бесконечную сумму.

         Ряд

                                         (2)

называется n-ым остатком ряда (1).

Свойства сходящихся числовых рядов.

         1. Из сходимости ряда (1) следует сходимость ряда (2) и обратно.

         2. Если сходится ряд (1) и а - некоторое действительное число, то сходится и ряд 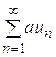, и его сумма равна aS, т.е. справедливо равенство  (здесь S - сумма ряда (1))

.

         3. Если сходятся ряды (1) и

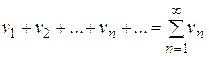,                                           (3)

имеющие, соответственно, суммы S  и s, то сходится и ряд 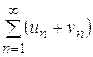, причём сумма его равна (S +s).

         4. Необходимое условие сходимости ряда.

Если ряд (1) сходится, то .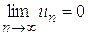

         5. Ряд, составленный из элементов геометрической прогрессии

,

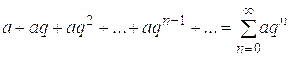сходится при 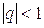, причём 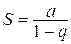, и расходится при 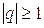. Его называют рядом бесконечной геометрической прогрессии.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2 Ряд Фурье. Общие понятия.

 

 

Идея о том, что любая периодическая функция может быть представлена в виде ряда гармонически связанных синусов и косинусов была предложена бароном Жан Батистом Жозефом Фурье (1768 − 1830).

 

 

Говорят, что функция f (x) имеет период P, если f (x + P) = f (x) для всех значений x. Пусть период функции f (x) равен 2π. В этом случае достаточно рассмотреть поведение функции в интервале [−π, π].

Предположим, что функция f (x) с периодом 2π абсолютно интегрируема в интервале [−π, π]. При этом является конечным так называемый интеграл Дирихле:

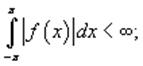
Предположим также, что функция f (x) является однозначной, кусочно-непрерывной (то есть имеет конечное число точек разрыва) и кусочно-монотонной (имеет конечное число максимумов и минимумов).

 Если условия 1 и 2 выполнены, то ряд Фурье для функции f (x) существует и сходится к данной функции (Смотрите об условиях сходимости также раздел Сходимость рядов Фурье).

 

 Если x0 − точка разрыва, то ряд Фурье сходится к значению

Ряд Фурье функции f (x) представляется в виде

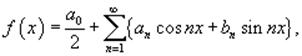
 где коэффициенты Фурье a0, an и bn определяются формулами

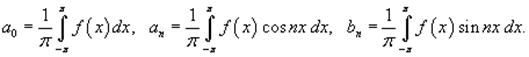
 Иногда используются альтернативные формы записи для разложения в ряд Фурье. Заменяя an и bn новыми переменными dn и φn или dn и θn , где

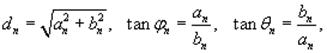
 можно, соответственно, записать

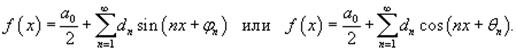
3 Ряды Фурье для четных и нечетных функций.

Отметим некоторые известные свойства чётных и нечётных функций.

 

1 Если функции      и     одновременно обе чётные или обе нечётные, то их произведение                  являются чётной функцией.

2 Если одна из функций         и        чётная, а другая нечётная, то их произведение           являются нечётной функцией.

 

3 Если         –нечётная на [–a;a] функция, то

 

4 Если         –чётная на [–a;a]  функция, то 

 

Учитывая эти свойства, разложение в ряд Фурье чётной или нечётной функции упрощается.

Пусть функция         –чётная и удовлетворяет теореме Дирихле. Тогда функции –чётны, а            –нечётные при любых n=1,2,... Поэтому

 

 

 

Ряд Фурье для чётной функции имеет вид:

 

 

 

Пусть функция         нечётная и удовлетворяет теореме Дирихле. Тогда функции                                .             нечётные, а

 

                        –четные при любых n=1,2,... Поэтому

 

 

 

Ряд Фурье для нечётной функции имеет вид:

 

.

 

 

 

 

 

 

 

 

 

 

 

 

4 Некоторые замечания разложения четных и нечетных функций

в ряд Фурье.

Свойства интеграла по симметричному промежутку от четных и нечетных функций позволяет упростить ряд Фурье.

Замечание 1.15. Пусть          – четная функция, определенная и интегрируемая на симметричном промежутке                        . Тогда

 

 

 

 

 

 

.

 

Интеграл от четной функции сводится к двойному интегралу от половины симметричного промежутка

 

 

Пусть           – нечетная функция, определенная и интегрируемая на симметричном промежутке                       . Тогда

 

 

 

 

 

Интеграл от нечетной функции по симметричному промежутку равен нулю:

 

 

 

Замечание 1.16. Пусть функция           – четная,        -периодическая, удовлетворяет условию теоремы Дирихле 1.1. Тогда ее ряд Фурье в действительной форме (1.21) в точках непрерывности имеет вид

 

 

так как, согласно формулам (1.33), (1.34), коэффициенты Фурье (1.22) преобразуются к виду:

 

 

 

 

 

 

 

 

 

 

 

 

т. е.

 

 

 

 

 

Если          – четная,        -периодическая, то ее ряд Фурье (1.24), (1.25) принимает вид:

 

 

 

 

 

 

 

 

 

 

 

Таким образом, четная функция, удовлетворяющая условиям теоремы Дирихле 1.1, раскладывается в ряд Фурье только по косинусам.

 

Замечание 1.17. Пусть функция        – нечетная,      -периодическая, удовлетворяет условию теоремы Дирихле 1.1. Тогда ее ряд Фурье в действительной форме (1.21) в точках непрерывности имеет вид

 

 

 

так как, согласно формулам (1.33), (1.34), коэффициенты Фурье (1.22) преобразуются к виду:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Если         – нечетная,      -периодическая, то ее ряд Фурье (1.24), (1.25) принимает вид:

 

 

 

 

 

 

 

 

Таким образом, нечетная функция, удовлетворяющая условиям теоремы Дирихле 1.1, раскладывается в ряд Фурье только по синусам.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Примеры разложения некоторых четных и нечетных функци в ряд Фурье.

Пример 1.

Разложить в ряд Фурье       -периодическую функцию, которая на промежутке  задана выражением                    .

Решение. Построим график функции (рис. 1.9).

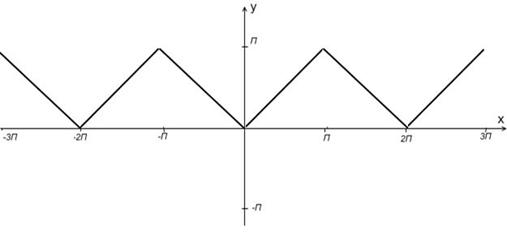
Рис.1.9. График функции к примеру 1

Функция четная, кусочно-монотонная, точек разрыва нет. Условия теоремы Дирихле 1.1 выполнены и как четная функция, она раскладывается в ряд (1.35)

в точках непрерывности, т. е. почти всюду

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Пример 2.

Разложить в ряд Фурье            -периодическую функцию, которая на промежутке                задана выражением                 .

Решение. Построим график функции (рис. 1.10).

Рис. 1.10. График функции к примеру 2.

Функция нечетная, кусочно-монотонна на промежутке              , имеет две точки разрыва 1-го рода                              :                – периодическая функция.

 

Условия теоремы Дирихле 1.1 выполнены и так как функция нечетная, то ее ряд Фурье (1.41) в точках непрерывности почти всюду сходится к значениям функции:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Пример 3.

Пусть функция f (x) имеет период 2π и раскладывается в ряд Фурье:

 

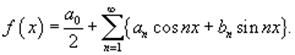
Вычислить коэффициенты a0, an и bn.

 Решение.

 Чтобы найти an, проинтегрируем ряд Фурье в интервале [−π, π]:

Для всех n > 0 справедливо

 

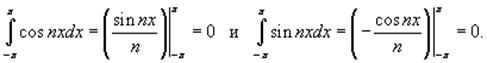
Поэтому, все члены в разложении Фурье справа от знака суммы равны нулю, что приводит к соотношению

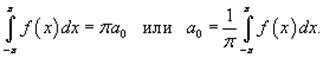
Чтобы определить коэффициенты an при m > 0, умножим обе части разложения в ряд Фурье на cos mx и проинтегрируем почленно:

Первое слагаемое в правой части равно нулю. Тогда, используя тригонометрические тождества, можно записать

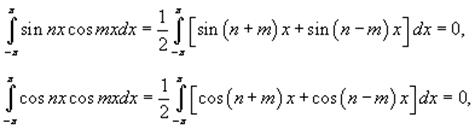
если m ≠ n.

 В случае, если m = n, получаем

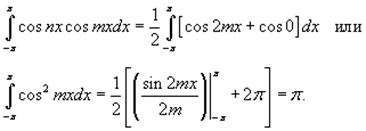
Таким образом,

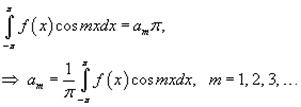
Аналогично, умножая ряд Фурье на sin mx и интегрируя почленно, получим выражение для bm:

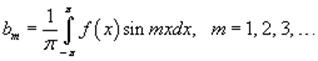
Переписывая формулы для an, bn, запишем окончательные выражения для коэффициентов Фурье:

Пример 4.

Найти разложение в ряд Фурье прямоугольной функции с периодом 2π, определенной в интервале [−π, π]:

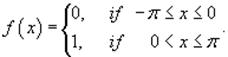
Вычислим сначала a0:

 Определим теперь коэффициенты Фурье при n ≠ 0:

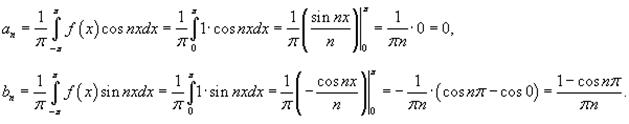
 Поскольку  , то можно записать

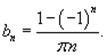
 Таким образом, разложение в ряд Фурье для прямоугольной функции имеет вид

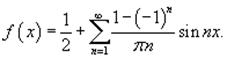
 Можно легко вычислить несколько первых членов разложения. Полагая, например, n = 5, получаем

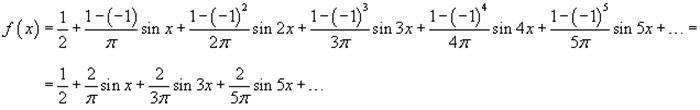
 На рисунке 1 представлены график данной функции и ее аппроксимация рядом Фурье при n = 10.

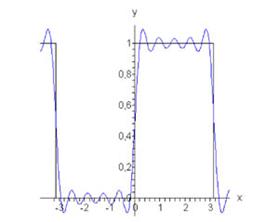
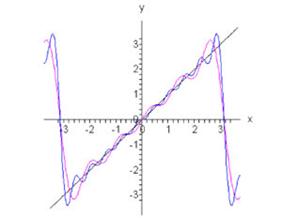
                            Рис.1, п=10                                                    Рис.2, п=5, п=10

 

Пример 5.

Предположим, что f (x) является периодической функцией с периодом 2π. Пусть 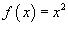 для  . Найти разложение Фурье для заданной параболической функции.

 Решение.

 Так как функция четная, то коэффициенты bn = 0. Тогда

 Применим дважды интегрирование по частям.

 Поскольку 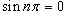  и 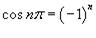 для натуральных n, то получаем

 

 Тогда разложение параболической функции в ряд Фурье имеет вид (рисунок 3)

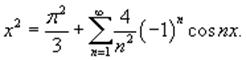
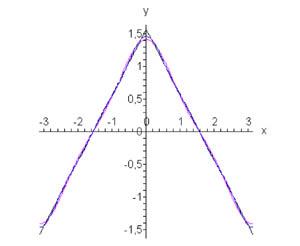
                       Рис.3, п=2, п=5                                            Рис.4, п=1, п=2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Список использованных источников

1.    http://www.sky-net-eye.com/rus/slovari/mathematics/fourier/theory/math_0004

2.    http://edu.dvgups.ru/METDOC/ENF/VMATEM/WM/METOD/UP/frame/1_4.htm

3.    http://abc.vvsu.ru/Books/u_vyssh_m2/page0036.asp

4.    http://www.dpva.info/Guide/GuideMathematics/SeriesOfTaylorMaklorenFourier/FourierSeries/

5.    http://ru.wikipedia.org/wiki/Ряд_Фурье

6.    http://www.math24.ru/definition-of-fourier-series.html

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Аннотация

           В реферате на тему «Ряд Фурье. Разложение в ряд Фурье четных и нечетных функций» рассмотрены основные определения, замечания и примерные решения некоторых задач на данную тему.

          Рядом Фурье элемента гильбертово пространства называют разложение этого элемента по ортогональному базису. Существует множество систем ортогональных функций: Уолша, Лагера, Котельникова и др. Разложение функции в ряд Фурье является мощным инструментом при решении самых разных задач благодаря тому, что ряд Фурье прозрачным образом ведёт себя при дифференцировании, интегрировании, сдвиге функции по аргументу и свёртке функций.

           Ряд Фурье позволяет изучать периодические (непериодические) функции, разлагая их на компоненты. Переменные токи и напряжения, смещения, скорость и ускорение кривошипно-шатунных механизмов и акустические волны - это типичные практические примеры применения периодических функций в инженерных расчетах.

             Разложение в ряд Фурье основывается на предположении, что все имеющие практическое значение функции в интервале -π ≤x≤ π можно выразить в виде сходящихся тригонометрических рядов.

           Говоря о разложении четных и нечетных функций нужно знать ,что функция y=f(x) четная, если f(-x)=f(x) для всех значений х. Графики четных функций всегда симметричны относительно оси у (т.е. являются зеркально отраженными). Функция y=f(x) нечетная, если f(-x)=-f(x) для всех значений х. Графики нечетных функций всегда симметричны относительно начала координат. Многие функции не являются ни четными, ни нечетными.