ЗМІСТ
ВСТУП
1.ВИХІДНІ ДАНІ 6
2.ОСНОВНА ЧАСТИНА 7
2.1. Розрахунок плоского настилу 7
2.2. Розрахунок балки настилу 8
2.3. Компоновка та підбір перерізу головної балки 11
2.4.Перевірка на міцність і жорсткість
підібраного перетину зварної балки 16
2.5.Розрахунок з"єднання поясів зі стінкою головної
Балки 18
2.6. Перевірка загальної і місцевої стійкості
елементів головної балки 19
2.7. Розрахунок зміни перетину головної балки
по довжині 21
2.8. Розрахунок кріплення балок настилу до
головної
балки
23
2.9. Розрахунок обпирання головної балки на колону 27
3.ВИСНОВОК ПО ПРОЕКТУ 29
4.ПЕРЕЛІК ВИКОРИСТАНИХ ДЖЕРЕЛ 31
 |
 ВСТУП
ВСТУП
Можна з певністю заявити, що на порозі третього тисячоліть зварювання – один з ведучих технологічних процесів. До 2/3 світового вживання металевого прокату йде на виготовлення зварних конструкцій та споруд. Зварюванню піддаються всі метали та неметали в будь-яких умовах-на землі, в морських глибинах та у космосі.
Балка є конструктивним елементом суцільного перетину, призначеним для роботи на поперечний вигин.
Балки застосовують в різних перекриттях, робочих майданчиках, мостах, підкранових балках і в інших конструкціях.
Балки служать для того, щоб сприймати навантаження і передавати їх на опори.
Балки прості у виготовленні. У них мала вартість виготовлення. Зручна конструктивна форма, невелика будівельна висота.
Найширше вживання балки знаходять для перекриття невеликих прольотів при великих навантаженнях. У разі великих прольотів і порівняно невеликих навантаженнях більш раціонально застосовувати крізні балки або ферми, що сприяє більш істотній економії металу.
Зварні балки звичайно складаються з трьох елементів: вертикального – стінки, і двох горизонтальних поясів (полиць), які приєднуються до стінки за допомогою зварки, як правило, автоматичної.
За статичною схемою балки класифікуються на розрізні, консольні і нерозрізні. В металевих конструкціях частіше застосовуються розрізні вільно оперті балки, нерозрізні балки і одно прольотні затиснені балки. Балки виготовляються з листової сталі і мають або двотавровий, або коробчатий перетин.
Елементи зварних балок можуть бути виготовлені з різних марок сталей. Стінку балки, що працює, в основному на вигин з незначними напругами, виготовляють з менш міцної і більш дешевої вуглецевої сталі, пояси – з низьколегованої високоміцної сталі.
 Елементи балки працюють на різні види навантаження.
Стінка двотаврової балки працює на стиснення, нижній пояс – на розтягування,
верхній пояс – на стиснення.
Елементи балки працюють на різні види навантаження.
Стінка двотаврової балки працює на стиснення, нижній пояс – на розтягування,
верхній пояс – на стиснення.
У наш час зварні конструкції знайшли широке вживання, тому що у зварних конструкцій є ряд переваг: економія металу до 10-15%, зниження витрат за рахунок зменшення кількості операцій.
Вдосконалення виробництва зварних конструкцій йде по шляху розробки і проектування ефективних конструктивних рішень, а також використовування при виготовленні і монтажі конструкцій нових зварювальних матеріалів, створення високомеханізованих і автоматизованих процесів збірки і зварки.
Використовуються також металеві заздалегідь напружені балки, в яких в результаті попередньої напруги стінки, забезпечується економія металу.
 1 ВИХІДНІ ДАНІ
1 ВИХІДНІ ДАНІ
Розрахувати нормальну балочну клітину робочого майданчика за наступними даними:
- проліт головної балки l1 = 18 м ;
- проліт балок настилу l2= 9м; на які укладений сталевий настил з рифленою поверхнею кроком а=1.0 м.
- нормативне корисне рівномірно-розподілене навантаження на майданчику рівне qon = 25кН/м2,
- коефіцієнт надійності по навантаженню γfp= 1,2
- об′єкт першого класу γn=1
. Коефіцієнт умов роботи γс=0,95.
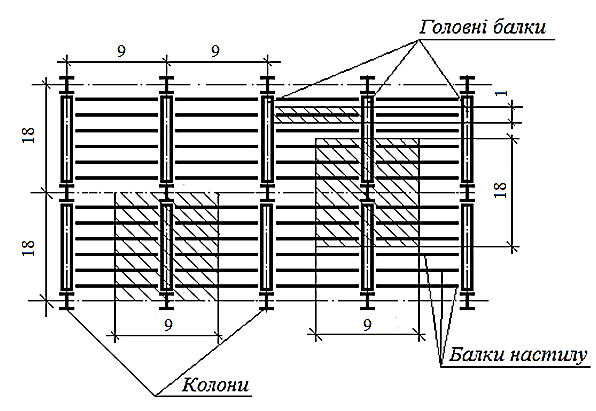
Рисунок 1.1 Розрахункова схема балочної клітини
2 ОСНОВНА ЧАСТИНА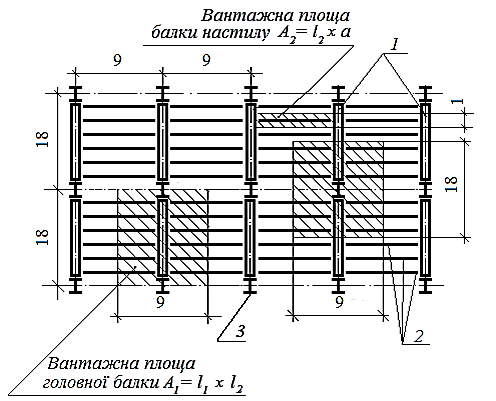
Рисунок 2.1Розподіл навантажень на елементи балочної клітини
1 – головні балки; 2 – балки настилу; 3 - колони
2.1 Розрахунок плоского настилу
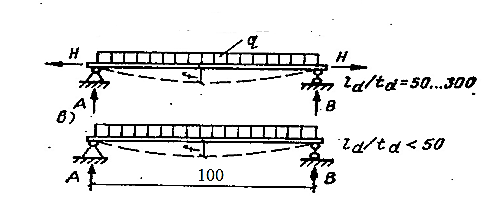
Рисунок 2.2Розрахунок настилу на згинання
Матеріал – сталь ВСт3пс6-2
2.1.1 Попередньо призначаю товщину рифленого настилу
td=14 мм, оскільки qon = 25кН/м2≥20кН/м2.
2.1.2 Власна вага настилу  gn=109,9·9,81 кг/м2 =1078,12 Н/м2
.
gn=109,9·9,81 кг/м2 =1078,12 Н/м2
.
2.1.3 Обчислюю нормативне навантаження на 1 см смуги настилу шириною b = 100 см.
qn1 = ( qon + gn1)b = (25 +1078,12)·1 = 261 Н/м
2.1.4 Оскільки qn1 = 261 Н/см > 100 Н/см, то розрахунок настилу при 1/ no= 1/150 ведемо на вигин.
2.1.5. Розраховую товщину настилу
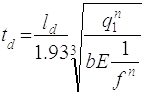
(2.1)

 де ld=a – довжина прольоту настилу, 100 см
де ld=a – довжина прольоту настилу, 100 см
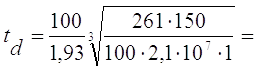 1.44cм
1.44cм
Приймаю листи настилу завтовшки td = 16мм.
2.1.6. Перевіряю прогин
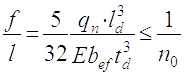

(2.2)
де ld - розрахункова довжина настилу 100см;
E1 = Е/(1-µ2)=2·105 /(1-0,32) =2,3·105 МПа - модуль
пружності;
bef- ширина смуги настилу, 100 см;
 td- товщина настилу, 1,0 см;
td- товщина настилу, 1,0 см;
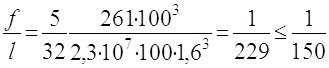
Умова жорсткості виконується.
2.2 Розрахунок балки настилу.
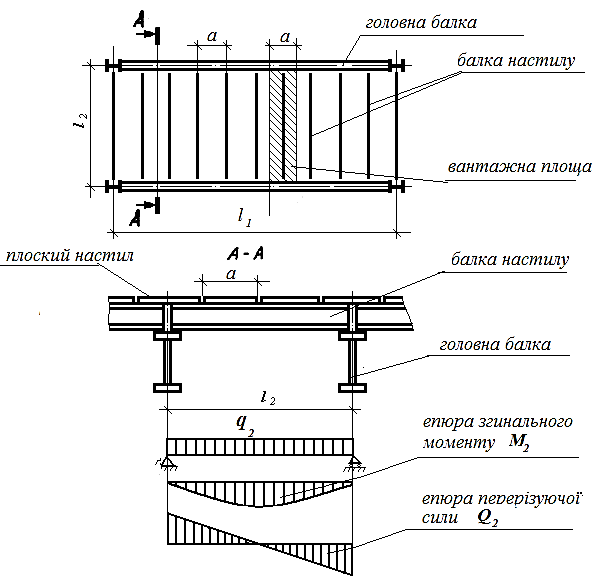
Рисунок 2.3До розрахунку головної балки
 2.2.1 Підбір перерізу прокатної балки
2.2.1 Підбір перерізу прокатної балки
2.2.1.1 Визначаю розрахункове навантаження на балку:
q2 = q onldγf0+gn1γfg · ld + gn2γfg, Н/м  (2.3)
(2.3)
де gn1 - власна вага настилу, 1,256кН/м2 ;
gn2- власна вага 1 м балки настилу, заздалегідь приймаю 0,3к Н;
γfg- коефіцієнт надійності по навантаженню, для власної ваги рівний 1,05;
l d - крок балок настилу, 100 см.
q2 = 25· 1,2·1,0+ 1078,12· 1,05· 1,0 + 0,3· 1,05 =31,6 кН/м
2.2.1.2 Визначаю максимальний згинаючий момент:
М 2 = ql22/8, кН/м (2.4)
де l2 - довжина балки настилу, 9м
М 2 = 31,6·9 2/8 = 320кНм
Поперечна сила
Q2=ql2/2=31.6·9/2=143кН
Необхідний момент опору перетину балки рівний
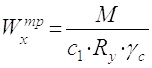
(2.5)
де с1 - коефіцієнт, залежний від форми перерізу, 1,1;
Ry - розрахунковий опір сталі ВСт3пс6-2, 270 Мпа
(27000 Н/см2).
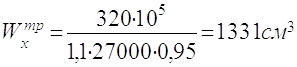
 2.2.1.3 За сортаментом приймаємо двотавр №
50, який має наступні геометричні характеристики: Wx=1598
см3, gn2= 785 Н/м,h=500мм,
Ix=39727см4,b=170мм,
tw =10мм,Sx=919 см3
2.2.1.3 За сортаментом приймаємо двотавр №
50, який має наступні геометричні характеристики: Wx=1598
см3, gn2= 785 Н/м,h=500мм,
Ix=39727см4,b=170мм,
tw =10мм,Sx=919 см3
2.2.1.4 Перевіряю мінімальну висоту балки з умови жорсткості
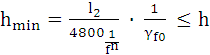
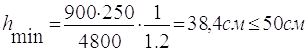
Умова виконується.
2.2.1.5 Перевірочні розрахунки
а) Розрахункове навантаження на балку з урахуванням власної ваги прокатної балки двотавра№50:
q21 =25·1,2·1,0+1078,12·1,05·1,0 +0,785·1,05=32,1кН/м
 |
б) Розрахунковий згинаючий момент
М21 =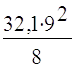 =325 кНм
(2.6)
=325 кНм
(2.6)
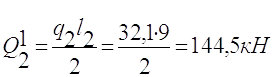
в) Виконуємо перевірку на міцність у двох напрямках:
- по нормальним напруженням:
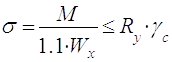
(2.7)

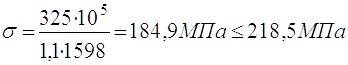
- по дотичним напруженням:
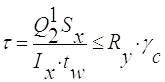 (2.8)
(2.8)
де Sx- статичний момент половини перерізу балки настилу відносно нейтральної осі,919 см3
Ix - осьовий момент інерції балки, 39727 см4
tw - товщина стінки балки, 1,0 см
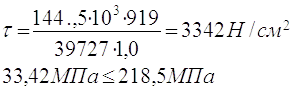
 Умова міцності виконується.
Умова міцності виконується.
г )Виконую перевірку на жорсткість:
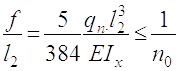
(2.9)
де qn2 - нормативне навантаження на балку
qn2= 25·1,0 + 1078,12·1,0 + 0,785 = 27,041 кН/м
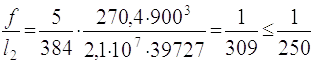
Умова міцності та жорсткості виконується.
2.3 Розрахунок головної балки.
2.3.1 Визначаю нормативне погонне навантаження:
qn = qon·l2 +gn1 · l2 + gn2 (l2/a) +gn3 , Н/м
де gn3– власна вага головної балки, заздалегідь приймаю 2% від навантаження, яке доводиться на балку;
 gn3=(25 +1078,12+0,785) 9 · 0,02 = 4,86 кН/м
gn3=(25 +1078,12+0,785) 9 · 0,02 = 4,86 кН/м
qn = 25 · 9 + 1078,12·9 + 0,785· (9/1,0) + 4,86 = =248 кН/м
Визначаю розрахункове погонне навантаження на головну балку:
q3 = q on∙γfp·l2 +gn1 γfg· l2 + gn 2 l2/(a) γfg+gn3 γfg,
 gn1 - власна вага настилу,
1078,12 кН/м2 ;
gn1 - власна вага настилу,
1078,12 кН/м2 ;
gn2- особиста вага балки настилу, 0,785кН/м;
gn3- власна вага головної балки, 4,86кН/м.
q3 =25·1,2·9+1078,12·1,05·9+0,785·(9/1,0)·1,05+4,86·1,05=294,4кНм
2.3.2 Визначаю:
максимальний згинаючий момент:
М1 = q3 l12/8, кНм (2.10)
М1 = 294,4·182 /8= 11923 кНм
максимальну поперечну силу:
Q1 = q3l1/2, кН
Q1 = 294,4·18 /2 = 2650кН
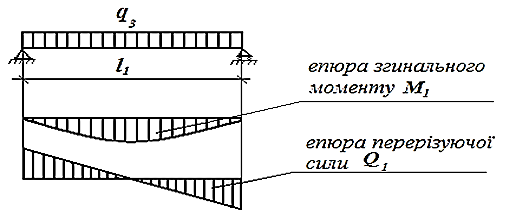
Рисунок 2.4До розрахунку головної балки
2.3.3 Визначаю необхідний момент опору:
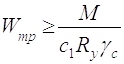
(2.11)
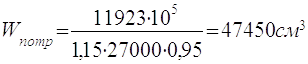
2.3.4 Компоновка складового перерізу балки
2.3.4.1 Будівельна висота не задана
2.3.4.2 Визначаю мінімальну висоту перетину балки з умови жорсткості
 |
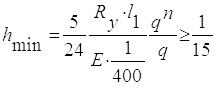
(2.12)

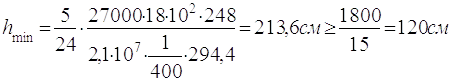
2.3.4.3 Визначаю максимальну товщину стінки по емпіричній формулі
tw1 = 7+3hmin, мм
tw1 = 7+3·2136/1000 =11,3 мм
Визначаю оптимальну висоту балки:
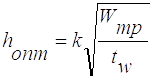
(2.13)
де Wтр - момент опору, 47450см3;
к- 1,15 для зварних балок
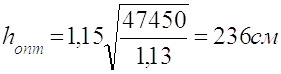
2.3.4.4 Призначаю висоту балки орієнтовно h= 2280 мм
2.3.5. Визначення товщини стінки tw.
2.3.5.1 Розраховуємо мінімальну товщину стінки балки з умов її роботи на зріз та зрівнюємо її з раніше призначеною tw1
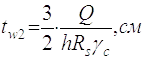 (2.14)
(2.14)
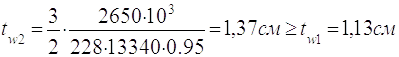
Де Rs=0,58Ry=0.58∙270=133,4 МПа
2.3.5.2 Обов’язкова умова:
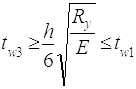 (2.15)
(2.15)
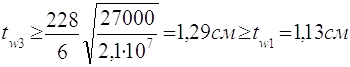
2.3.5.3 Приймаємо товщину стінки tw = 14 мм.
Прийнята товщина стінки задовольняє наступні вимоги:
tw=1,4см›tw2=1,37см
tw=1,4 см ≥ tw1=1,13 см
tw=1,4см ≥ tw3 =
1,29см
Висновок: Прийнята товщина стінки балки відповідає співвідношенню h w = 2281,4=163
2.3.6 Визначаю розміри поясів.
2.3.6.1 Приймаю товщину поясу tf=40 мм
tw≤ tf≤3 tw1,4 см ≤4см ≤3∙1,4= 4,2см
2.3.6.2
а) Потрібний момент інерції площі перерізу балки:

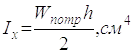 (2.16)
(2.16)
hw=228-2∙4=220 см
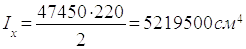
б) Момент інерції стінки
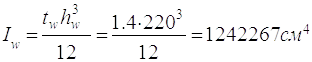
Момент інерції поясів
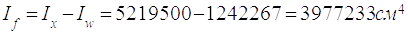
в) Орієнтовна площа перерізу поясного листа
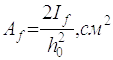
Де h0 = h- tf=228-4=224 cм

2.3.6.3 Розраховую ширину поясу балки:
а) потрібна ширина:
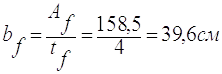
б) визначена з загальної стійкості балки:
(2.17)
 |
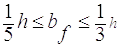
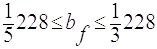
45,6≤ bf≤ 76
 |
в) з технологічних міркувань:
456 мм ≤bf ≤ 760 мм
Приймаємо ширину поясу bf=530мм
456 мм≤530 мм ≤ 760 мм
Умови виконуються
г )Приймаю ширину поясного листа відповідно стандартного ряду ширини прокатного листа bf =530 мм
2.3.6.4 Перевіряю прийняту ширину поясу виходячи з забезпеченням місцевої стійкості.
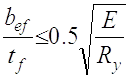
де 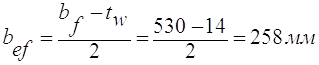
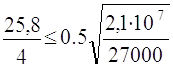
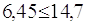
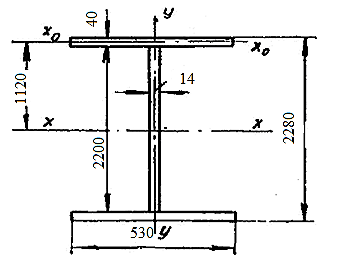
Рисунок 2.5Переріз головної балки
Умова виконується.
2.4 Перевірка на міцність і жорсткість підібраного перетину зварної балки.
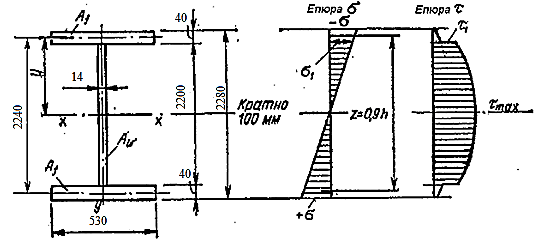
Рисунок 2.6 Епюри нормальних та дотичних напружень по висоті балки.
2.4.1 Призначивши остаточні розміри перерізу балки, виконуємо перевірку його міцності, розраховуючи нормальні напруження в місці діяння максимального згинаючого моменту та максимальні дотичні напруження на опорі у такій послідовності:
2.4.1.1 Визначаю момент інерції:
I x = tw·hw3/12 + 2Af а2, см4 (2.18)
 де а=hw/2 + tf/2=220/2 +4/2 =112 см
де а=hw/2 + tf/2=220/2 +4/2 =112 см
 |
tw - товщина стінки,1,4см
hw– висота стінки, 220 см
Аf - площа поясу, 53 х 4 =212 см2;
Ix = 1,4·2203/12 + 2·212∙1122 =1242267+5318656=6560923см4
2.4.1.2 Визначаю момент опору:
Wx = 2Ix/h, см3 (2.18)
Wx= 2·6560923/228 = 57552 см3
Перевіряю балку на міцність по нормальним напруженням
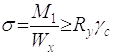 (2.19)
(2.19)
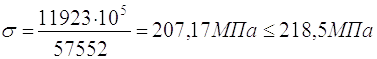
2.4.1.3. Визначаю статичний момент:
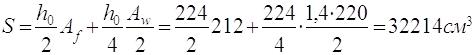
2.4.1.4. Перевіряю балку на міцність по дотичнім напруженням
τ = QS/Ixtw˂Rsγc, Н/см2 (2.20)
τ=(2650·103·32214)/(6560923·1,4)≤133,4·0,95
92,9 МПа ≤120,06Мпа
Умова міцності виконується
2.4.2.1 Виконую перевірку балки на прогин по формулам другої групи граничних станів
 Розраховую масу 1 м балки
Розраховую масу 1 м балки
- без ребр жорсткості:
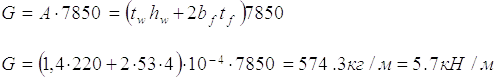
- з ребрами жорсткості:
g3n1 =1,03G=1,03∙5,7 =5,9кН/м
2.4.2.2 Відносний фактичний прогин балки f/l не повинен перевищувати граничне нормативне значення 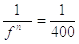
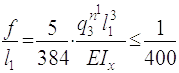
(2.21)
де qn13= qon·l2+gn1 · l2 + gn2 (l2/a) +gn13 , Н/м
qn13 = 24 · 9 + 261·9 + 0,785· (9/1,0) + 4,687 =240 кН/м
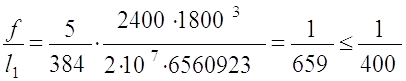
Розрахункове навантаження:
q3=24000·1,22·9+1256·1,05·9+785·(9/1,0)·1,05+5600·1,05=
=288686Н/м =288,7 кН/м
Умова виконується, жорсткість балки забезпечена.
2.5 Розрахунок з"єднання поясів із стінкою головної балки 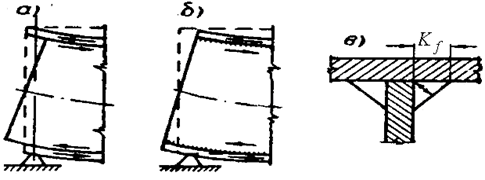
Рисунок 2.7До розрахунку з’єднань поясів зі стінкою балки
 Визначаємо зусилля зсуву:
Визначаємо зусилля зсуву:
Т = Q Sf / Ix, кн. (2.22)
Статичний момент полиці щодо нейтральної осі рівний.
Sf = Afh0/2 ,см3
h0 = hw + tf = 220 + 4 = 224 см
Sf = 212∙224/2 = 23744см3
Визначаю мінімальну товщину шва, що прикріплює пояс до стінки, при lw=1см:
kf = QSf/ nIx(βRw) minγc≥4 мм (2.23)
де (βRw) min– менше з добутку коефіцієнта глибини проплавлення на розрахунковий опір
βfRwf= 0,7∙18000=12600 Н/см2
βzRwz = 1∙0.45∙37000=16670Н/см2
kf =2590·103·23744/2·6560923·12600∙0,9 = 0,413см≥0,4 см
Призначаємо конструктивно мінімальну товщину шва kf = 10 мм
2.6. Перевірка місцевої і загальної стійкості елементів головної балки
2.6.1. Головна балка розкріплює балками настилу через а=1,0 м.
Перевіряю відношення
1≤h0 /bf≤ 6 1≤224/53≤ 6 1≤4,2≤ 6
та 15≤bf/tf≤ 35 15 ≤ 53/4 ≤ 35 15≤13,25≤ 35
Умова виконується.
l ef/bf≤δ (0,41+0,0032bf /tf + (0,73 – 0,016bf /tf)bf/ h0)√(E/Ry);
де δ = 1,0 для перетину балок, що працюють пружно
 100/53≤1·
(0,41+0,0032·53/4+(0,73–0,016·53/4) ×
100/53≤1·
(0,41+0,0032·53/4+(0,73–0,016·53/4) ×
 |
×53/224√(2,06· 107/27000);
1,89<17,65
Умова дотримується, перевірка балки на загальну стійкість не потрібна.
2.6.2.1 Визначаю стійкість стислого поясу
bef/tf< 0,5√(E/Ry) (2.24)
де bef - звіс поясу, см;
bef= (53,0-1,4)/2= 25,8 см
25,8/4< 0,5 √(2.1·107/27000
6,45<15,56
Умова виконується, стійкість поясу забезпечена.
 2.6.2.2 Перевіряю стійкість стінки балки.
2.6.2.2 Перевіряю стійкість стінки балки. 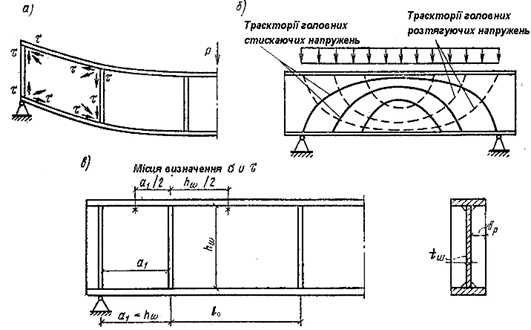
Рисунок 2.8 До розрахунку ребр жорсткості
Визначаю необхідність постановки ребр жорсткості
λw = ( hw/ tw ) √(Ry/E)≤ 3,2 (2.25)
де hw - розрахункова висота стінки, 220см;
λ w = (220 /1,4) √(27000/2,1∙107) = 3,2= 3,2
Умова стійкості виконується.
Конструктивно призначаю поперечні ребра жорсткості з кроком l0< 2,5hwпри λ < 3,2:
l0< 2,5hw = 2,5 · 220=550 см
Конструктивно пов"язую розташування ребр з кроком настилу. При кроці балок настилу1,0 м ребра розташовую через два кроки, тобто через2,0 м.<5,5 м
2.6.5 Визначаю розміри ребра жорсткості
Ширина ребра
br>hw/30 + 40 ≤(bf–tw)/2, мм; (2.26)
br>220/30 + 40 ≤(530 –14)/2
br≥47,33 ≤ 258
приймаємо br = 240 мм
Товщина ребра:
tr> 2br √(Ry/E)
tr> 2∙24∙√(27000/2,1∙107)= 1,4 см.
 Приймаємо товщину ребр жорсткості tr
= 14 мм
Приймаємо товщину ребр жорсткості tr
= 14 мм
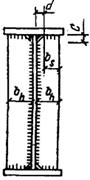
Рисунок 2.9 Ребро жорсткості
2.7 Розрахунок змінення перерізу головної балки по довжині
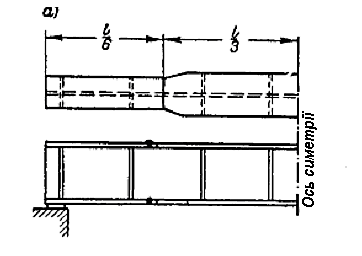
Рисунок 2.10 Зміна
перерізу по довжині балки
2.7.1. Призначаю стик на відстані 1/6 прольоту від опори.
Х=18/6=3м
2.7.2 Зменшена ширина поясів повинна складати
не менше bf1 ≥180 мм і не менше bf1≥bf/2, а також повинне додержуватися співвідношення bf1≤h /10;
b f1≥53/2 = 26,5 см, b f1≤h/10 = 228/10=22,8 см
Приймаю bf1 = 280 мм
bf1 = 280мм≥180 мм ; bf1 = 280мм≥ 220,8/2 = 110мм;
bf1 = 280мм≥h/10 = 228/10=228мм
Приймаю перетин поясів 40х280 мм
2.7.3 Визначаю розрахунковий момент і поперечну силу в перетині на відстані х = 3 м.
Розрахунковий момент:
M1 = q13x (l-x)/2 = 288,7 · 3,0(18-3)/2=6496 кНм
Поперечна сила:
Q11 = q(l/2 –x)= 288,7(18/2-3)= 1732кН
2.7.4 Перевіряю міцність зміненого перетину.
2.7.4.1 По нормальним напруженням:
Момент інерції зміненого перетину:
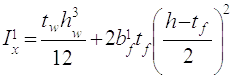

(2.27)

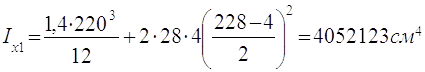
Момент опору зміненого перетину:
Wx1 = 2Ix1 /h= 2 · 4052123/228 = 35540см3
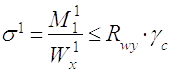
(2.28)
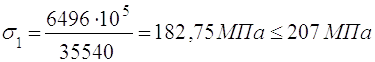
Умова міцності виконується.

 2.7.4.2 По дотичним напруженням:
2.7.4.2 По дотичним напруженням:
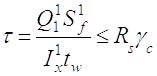
Статичний момент площі поперечного перетину:
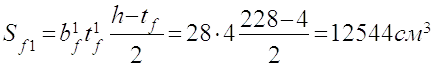 (2,29)
(2,29)
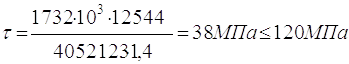
Умова міцності виконується.
2.7.4.3 По приведеним напруженням:
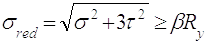 (2,30)
(2,30)
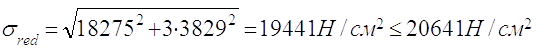
Умова міцності виконується.
2.7.4.4 Розрахунок економії металу
а)маса балки зміненого перетину
G1 = (Aw + 2Af)(l1-2x)7850+2(Aw +2Af1) x7850, кг (2.31)
G1=(2,2∙0,014+2∙0,53∙0,04)(18-2∙3)7850+
2(2.2∙0,014+2∙0,28∙0,04)∙3∙7850 = 9495,36 кг
б)маса балки постійного перетину
G= (Aw + 2Af)l1∙7850, кг (2.32)
G= (2,2∙0,014 + 2∙0,53∙0,04)18∙7850=10343,16 кг
Економія металу рівна:
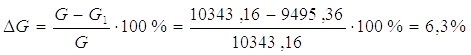
 2.8 Розрахунок прикріплення балок настилу до
головних балок
2.8 Розрахунок прикріплення балок настилу до
головних балок
Вузол кріплення балок настилу до головної балки приведений на
Малюнку.
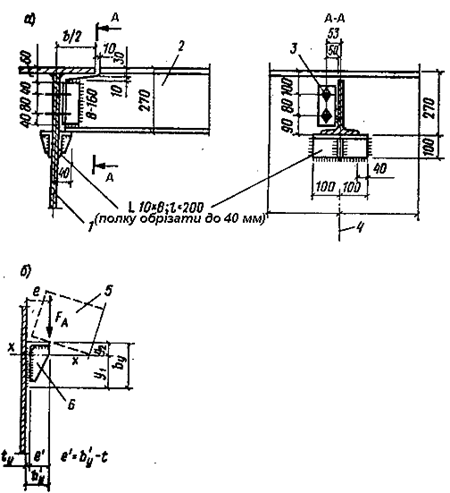
Рисунок 2.11 Кріплення балки настилу до головної балки
а – деталь кріплення; б – розрахункова схема опорного столику
(1 – головна балка; 2 – балка настилу; 3 – болт Æ16, отвір Æ19; 4 – вісь балки настилу; 5 – балка; ребро жорсткості опорного столика )
2.8.1 Визначаю опорну реакцію:
FA = q2l2/2, кн. (2.33)
FA = 31,6 ∙9/2=141,3кН
2.8.2. Розрахункову довжину зварного шва на одній стороні опорного столика обчислюю при зусиллі 2/3FA
lw = 2FA/ (3βfkfRwfγc ) , см (2.34)
де βf - коефіцієнт глибини проплавлення, для автоматичного зварювання рівний 0,7;
kf - катет кутового шва, приймаю конструктивно 6 мм;
Rwf - розрахунковий опір металу шва для автоматичного зварювання 18000 Н/см2.
lw = 2∙141,3∙103/ 3∙0,7∙0,6∙18000∙0,9 =13,8 см
2.8.3 Конструктивно приймаємо рівнобічні кутники 160х10з обрізанням на половину ширини опорної полиці.
Довжина кутника дорівнює ширині полиці двотавра балки плюс 80 мм
ly = bf+80, мм
ly = 170+80=250мм
Приймаємо довжину кутника ly = 250мм = 25см.
2.8.4 Для запобігання вигину укороченої полиці кута ставимо по осі ребро жорсткості завтовшки t2 = 8 мм .
Такий же кутник передбачаємо на стінці балок настилу. Його довжину визначаємо з умови розміщення двох монтажних болтів.
 При вживанні болтів діаметром 16 мм мінімальна довжина
кутана стінці буде:
При вживанні болтів діаметром 16 мм мінімальна довжина
кутана стінці буде:
la = 2·2d0 + 3d0, см
де d0 - діаметр отвору під болти, 19 мм;
2d0 – мінімальна відстань до краю елемента;
3d0 - мінімальна відстань між центрами отворів
ly = 2∙2∙19+3∙19 = 133мм
Приймаю довжину кутника 150мм
2.8.5 Перевіряю міцність верхньої полиці кутника від дії згинаючого моменту. Вважаємо, що опорна реакція при прогинанні балки діє на зовнішню кромку полиці опорного столика з экцентристетом = by1 = 8 см, а по відношенню до внутрішньої грані кутника e1 = b1у- t = 8,0-1,0 = 7см
M = FAe = 141,3∙103∙8 = 1130400Нсм= 11,3кНм
M1= FAe1= 141,3∙103∙7 = 989100Нсм = 9,9кНм
Визначаю необхідний момент опору опорного столика:
W = M1/Ryγc = 9,9∙105/27000∙0,9 = 47,8 см3
 |
Для полиці, посиленої ребром жорсткості tr = 8 мм, визначаю момент опору W.
Площа таврового перетину з полицею зверху
Аf= l у t + trhr, см2 (2.35)
hr=by-2t = 16-2∙0.8 =14,4 см
А f = 25,0∙1,0+0,8∙14,4 = 36,5см2
Статичний момент перетину щодо осі, що проходить через центр ваги полиці
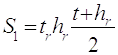




(2.36)
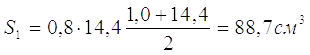
Відстань z1 від осі полиці до центру ваги перетину
z 1 = S1/Af= 88,7/36,5 = 2,4см
Момент інерції перетину
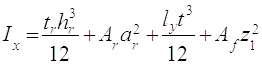
(2.37)
ДеAr=tr h r =0,8∙14,4=11,52 cм2
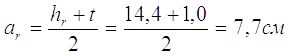
Af=t∙ly=1,0∙25,0=25см2
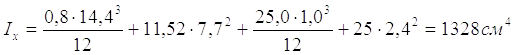
Моменти опору перетину.
Верхньої частини:
 W1 = Ix/y2 =
1328/2,9=457см3
W1 = Ix/y2 =
1328/2,9=457см3
y2 = z1 + t/2= 2,4+1,0/2 = 2,9см
Нижньої частини:
у1 = hr– (z1-t/2) = 14,4-(2,4-1,0/2)= 12,5см
W2 = Ix/y1 = 1328/12,5 = 106см3, що більше, ніж необхідний момент опору W =47,8см3
Умова міцності виконується.
2.8.6 Перевіряю міцність зварного шва опорного столика на дію опорної реакції FAі моменту
М= FAb1y==141,3∙103∙8=1130000Нсм
а) по металу шва:
τ w= FA/(lwβwfkf), Н/см2 (2.38)
τw = 141,3∙103/∙30∙0,7∙0,6 = 11214Н/см2 = 11,2кН/см2
lw = 2(by– 1 ), см;
lw = 2(16-1)= 30 см
σw = M/Ww = 11,3∙105/63=6695 Н/см2 = 6,7кН/см2
Ww = 2(βfkflw2/6)= 2(0,7∙0,6∙152/6)=63см3
lw = bу-1 = 16-1 = 15см
Сумарне напруження від сумісної дії згинаючого моменту і поперечної сили:

 σ =√σ2+3τ2=√6,7
2+3∙11,22=155,40 МПа
σ =√σ2+3τ2=√6,7
2+3∙11,22=155,40 МПа
Rwfγс=180∙0,9=162МПа
155.40МПа˂162МПа
Умова міцності виконується.
2.9 Розрахунок обпирання головної
балки на колону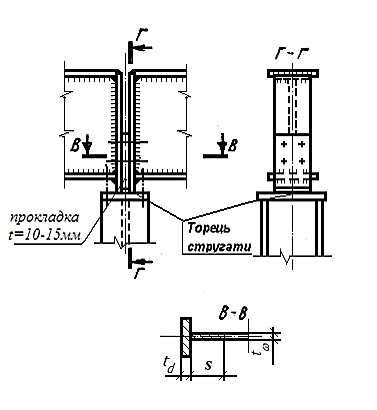 Рисунок 2.12 Обпирання
головної балки на колону
Рисунок 2.12 Обпирання
головної балки на колону
2.9.1 Головна балка спирається на колону зверху і кріпиться до оголовкуна болтах. Опорний торець балки приструганий.
2.9.1.1 Визначаю необхідну площу зминання:
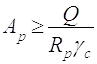
(2.39)
де Rp = Ru =36000Н/см2
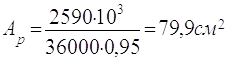
2.9.1.2
Ширина одного ребра
 br = ( bf1 -tw )/2 = (28-1,4)/2=13,3 см
br = ( bf1 -tw )/2 = (28-1,4)/2=13,3 см
Ширина торцевої діафрагми
bd = bf1=28см
2.9.1.3 Товщина опорного ребра.
- торцевої діафрагми:
td=Ар/2bs =79,9/2∙9,3=4,29 см
де bs = br–d = 13,3-4,0=9,3 см
 де d = 40 мм–катет скосу для поясного шва
де d = 40 мм–катет скосу для поясного шва
td=Ар/bd=79,9/28=2,85 см
Приймаю товщину торцевої діафрагми 30 мм
2.9.1.4 Вибираю опорний вузол з опорною діафрагмою, оскільки товщина діафрагми менше товщини опорних ребр.
2.9.2. Перевіряю діафрагму на стійкість
2.9.2.1 Умовна площа таврового перетину опорного стояку:
 |
As=Stw + bdtd
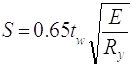
(2.40)
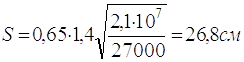
As=26,8∙1,4+28∙3,0=121,5cм2
2.9.2.2 Момент інерції площі поперечного перетину щодо осі Z без урахування моменту інерції частини стінки:
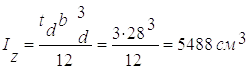
2.9.2.3 Радіус інерції:
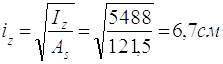
2.9.2.4 Гнучкість стояку:
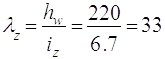 →φ = 0,932
→φ = 0,932
2.9.2.6 Перевіряю умовну опорну стійку діафрагми на поздовжнє згинання
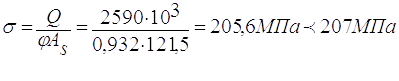
Умова міцності виконується.
 2.9.2.7 Визначаю катет шва:
2.9.2.7 Визначаю катет шва:

(2,41)
де Δ = 60 мм
(βRw)min– менше з твору коефіцієнта глибини проплавлення на розрахунковий опір
βfRwf= 0,7∙18000=12600 Н/см2
βzRwz = 1∙0.45∙37000=16670Н/см2
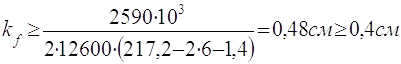
Приймаю катет шва рівний 6 мм.
ВИСНОВКИ ЗА ПРОЕКТОМ
 |
Розрахував і спроектував зварну балку перекриття, несучу рівномірно розподілене навантаження, яке складається з постійного корисного навантаження q0n = 25кН/м2 з коефіцієнтом надійності навантаження γfp = =1,25. Матеріал вибрав – сталь марки ВСт3пс6-2, Ry = 270 мПа. Граничні відносні прогини прийняв: для головних балок – 1/n0 = 1/400; для балок настилу – 1/n0 = 1/250; для настилу – 1/n0 = 1/150, ширина смуги настилу b=100см, l1 = 18 м, l2 = 9 м.
В залежності від корисного навантаження обрав товщину настилу 14 мм. При перевірочних розрахунках одержав товщину настилу 16 мм. При перевірці настилу на жорсткість відносний прогин складає 1/229, що менше допустимого прогину 1/150.
Після коригування розрахункового навантаження з урахуванням власної ваги настилу за умовою міцності підбираю переріз балки настилу за прокатним профілем двотавру №50 виписавши з сортаменту його основні геометричні характеристики.
Після уточнення навантаження з урахуванням власної ваги обираю переріз балки настилу та уточнюю розрахунковий згинаючий момент та поперечну силу, проводжу остаточний розрахунок на міцність та жорсткість обраного перерізу.
Висновок: обраний переріз балки настилу з прокатного профілю двотавра №50 задовольняє умови міцності та жорсткості.
Розрахунок головної балки, після визначення нормативного та розрахункового погонного навантаження , починаю з визначення потрібного моменту опору перерізу балки за умови міцності по нормальним напруженням, який складає 47450 см3.
В процесі розрахунку я визначив висоту балки, виходячи з двох умов:
- якнайменшої витрати металу - hopt=2060 мм;
- необхідної жорсткості - hmin=2136 мм.
Остаточно приймаю висоту стінки балки 2280 мм.
По емпіричній формулі розрахував товщину стінки і перевірив прийняті розміри стінки з умови дії дотичних напружень. Остаточно прийняв товщину стінки 14 мм.
Знайшов ширину поясів bf.=530мм та товщину поясів 40 мм. Перевірив їх з умови
стійкості. Підібраний перетин балки перевірив на міцність і жорсткість по
нормальним і дотичним напруженням і  з"ясував, що матеріал балки забезпечує її міцність та
жорсткість. Визначив катети швів, що сполучають стінку з поясом kf=10мм. При перевірці стійкості елементів балки визначив
необхідність конструктивної установки ребр жорсткості. Розрахував розміри ребр
жорсткості.
з"ясував, що матеріал балки забезпечує її міцність та
жорсткість. Визначив катети швів, що сполучають стінку з поясом kf=10мм. При перевірці стійкості елементів балки визначив
необхідність конструктивної установки ребр жорсткості. Розрахував розміри ребр
жорсткості.
Розрахував прикріплення балок настилу до головних балок.
Балки настилу опираються на столик з кутників 160х10 довжиною 250 мм, що приварені до стінки головної балки Розрахував зміну перетину балки по довжині. Зменшений переріз поясу 40х280 мм знаходиться на відстані 3 м від опор балки .
Перевірив напруження в зменшеному перетині балки. Умова міцності виконується, загальна стійкість балки на перетині забезпечується.
Для розрахунку обпирання головної балки на колону розрахував опорну діафрагму на зминання торцевої поверхні і на стійкість. Визначив катет шва, що прикріплює діафрагму до торця балки.
За даними розрахунку накреслив загальний вигляд зварної головної балки та розрахував витрати металу на її виготовлення.
 СПИСОК ВИКОРИСТАНОЇ ЛІТЕРАТУРИ
СПИСОК ВИКОРИСТАНОЇ ЛІТЕРАТУРИ
1.Мандрыков А.П. Примеры расчета металлических конструкций. -М.: Стройиздат.-1991.- 431 с.
2. А. М. Михайлов « Сварныеконструкции №,-М.; Стройиздат,1983.-367 с.
3. Е.И. Беленя «Металлические конструкции» - М.; Стройиздат, 1986.-560 с.
4. Васильев А.А. «Металлические конструкции». - М.:Стройиздат.- 1979.- 472 с.
5.СНиП II – 23 - 81. Стальные конструкции. Нормы проектирования. - М.: Стройиздат.- 1982 .- 93 с.













 (zip - application/zip)
(zip - application/zip)










