Разработка приложения с графическим интерфейсом для вычисления определенного интеграла функции

Санкт-Петербургский политехнический университет Петра Великого

Институт энергетики и транспортных систем

Кафедра «Атомная и тепловая энергетика»

ЗАДАНИЕ

НА КУРСОВУЮ РАБОТУ

по дисциплине «Информационные технологии»

студенту ________________________________________________

Тема «Разработка приложения с графическим интерфейсом для вычисления определенного интеграла функции»

1. Исходные данные

- Ануфриев И. Е., Смирнов А. Б., Смирнова Е. Н. MATLAB 7. - СПб.: БХВ-Петербург, 2005. 1104 с.

- реализовать и сравнить методы численного интегрирования:

2. Содержание пояснительной записки

- введение;

- математическое и алгоритмическое описание методов решения задачи;

- создание приложения с графическим интерфейсом (алгоритм работы приложения и обработки событий, результат работы приложения для тестового задания);

- исследование и сравнение методов численного интегрирования;

- заключение;

- приложения (листинг программы, руководство пользователя).

1.     введение

Matlab – это система инженерных и научных вычислений. Она обеспечивает математические вычисления, визуализацию научной графики программирование и моделирование процессов с использованием интуитивно понятной среды окружения, когда задачи и их решения могут быть представлены в нотации, близкой к математической. Наиболее известные области применения системы Matlab:

·         математика и вычисления;

·         разработка алгоритмов;

·         вычислительный эксперимент, имитационное моделирование, макетирование;

·         анализ данных, исследование и визуализация результатов;

·         научная и инженерная графика;

·         разработка приложений, включая графический интерфейс пользователя.

Основным объектом при программировании в среде Matlab является массив, для которого не требуется указывать размерность явно. Это позволяет решать многие вычислительные задачи, связанные с векторно-матричными формулировками.

Система Matlab – это одновременно и операционная среда и язык программирования. Пользователь может написать специализированные функции и программы, которые оформляются в виде М-файлов. По мере увеличения количества созданных программ возникают проблемы их классификации и тогда можно попытаться собрать родственные функции в специальные папки. Это приводит к концепции пакетов прикладных программ, которые представляют собой коллекции М-файлов для решения определенной задачи или проблемы.

Cреда системы Matlab

Среда системы Matlab это совокупность интерфейсов, через которые пользователь поддерживают связь этой системой. Это: диалог посредством командной строки или графического интерфейса, просмотр рабочей области, редактор и отладчик М-файлов, работа с файлами и оболочкой DOS, экспорт и импорт данных, интерактивный доступ к справочной информации, динамическое взаимодействие с внешними системами Microsoft Word, Microsoft Excel и др. Реализуются эти интерфейсы через командное окно, инструментальную панель, системы просмотра рабочей области и путей доступа, редактор / отладчик М-файлов, специальные меню.

Пользовательский интерфейс носит дружественный характер и построен с учетом устоявшихся принципов программного обеспечения, разрабатываемого для операционной системы Windows.

В системе Matlab существует два вида м-файлов:

·         скрипты – представляют последовательности команд (представляют собой процедуры);

·         function – представляют собой функции с входными аргументами и выходными параметрами (значениями функции).

Но далее возникает необходимость многократного запуска файла программы при других, изменённых параметрах решаемой задачи. Возникает неудобство: в постоянном редактировании исходного текста программы и повторном или очередном её запуске. При этом важен механизм управления переменными, который бы обеспечивал удобный интерфейс между программой и пользователем. При решении других задач могут возникнуть трудности с визуализацией какого-либо процесса, то есть некоторая переменная изменяться динамически в процессе решения поставленной задачи.

Все эти и другие трудности, возможно, решить при использовании графического интерфейса пользователя. (GUI – Graphical UserInterface)

Основные принципы построения графического интерфейса

Использование графического интерфейса позволяет пользователю сделать программу более универсальной.

Как и любой процесс проектирования, процесс построения графического интерфейса пользователя можно разбить на следующие этапы:

1. Постановка задачи,

2. Создание формы интерфейса и создание на неё элементов управления.

3. Написание кода программы и кода обработки событий.

Этапы построения графического интерфейса пользователя

1. На первом этапе проводиться анализ поставленной задачи и определяется количество и состав элементов управления необходимых для решения задачи.

2. На втором этапе создаётся форма графического интерфейса и на ней создаются и размещаются элементы управления. Здесь же описываются их свойства.

Задавать расположение и выравнивать элементы на форме описывать их свойства можно "вручную", но для удобства и быстроты используют редактор выравнивания объектов (The Alignment Tool) и редактора свойств (The Property Editor).

Существует два способа создания формы и элементов управления, а так же задания или изменения их свойств:

·         использование команды WORKSPACE (то есть использование команды операционной среды MATLAB).

·         использование средств панели инструментов – совокупности средств для быстрого создания GUI (The Control Panel).

При построении элементов управления первым способом удобно использовать скрипт-файл, в котором последовательно с помощью команд WARKSPACE описывается создание элементов управления и устанавливаются их свойства.

Эти команды можно использовать как для написания кода, создающего графический интерфейс пользователя, так и использовать для управления свойствами элементов управления из тела m-файлов. Благодаря чему мы можем получить визуализацию нашего процесса вычисления.

На практике всё более склоняются ко второму способу создания графического интерфейса с элементами управления. Это объясняется тем, что при использовании панели управления с её редакторами свойств, событий, выравнивания очень удобно работать, и создавать GUI значительно быстрее, чем в первом случае.

3. На третьем этапе создания графического интерфейса пользователя (GUI) пишется код основной программы вычисления и код для обработки событий.

Код основной программы вычисления, пишется на языке программирования операционной среды Matlab, в виде m-файла. Созданные m-файлы закрепляются за событием какого-нибудь элемента управления или формы.

При описании свойств элементов управления события описываются в m-файле:

а) либо при создании каждого элемента управления описываем его свойства и сразу описываем действие событие;

б) либо описываем обработку события для каждого элемента при помощи редактора событий (The Property Editor).

Начало выполнения действий по созданию графического интерфейса

Редактор GUIDE (руководство) вызывается командой guide из командного окна или путем выполнения цепочки команд главного меню File (Файл) – New (Новый) – GUI (Графический Интерфейс).

2.создание приложения с графическим интерфейсом (алгоритм работы приложения и обработки событий, результат работы приложения для тестового задания);

 Графический пользовательский интерфейс MATLAB

В состав MATLAB входит среда GUIDE (Graphical User Interface Development Environment) для создания приложений с графическим интерфейсом пользователя. Работа в этой среде достаточно проста - элементы управления (кнопки, раскрывающиеся списки и т.д.) размещаются при помощи мыши, а затем программируются события, которые возникают при обращении пользователя к данным элементам управления.

Приложение может состоять как из одного основного окна, так и нескольких окон и осуществлять вывод графической и текстовой информации, в основное окно приложения и в отдельные окна. Ряд функций MATLAB предназначен для создания стандартных диалоговых окон открытия и сохранения файла, печати, выбора шрифта, окна для ввода данных и др., которыми можно пользоваться в собственных приложениях.

Что необходимо знать для создания приложений с графическим интерфейсом? Во-первых, как программируются файл- функции с подфункциями, файл- функции с переменным числом входных и выходных аргументов. Во-вторых, требуется иметь представление об иерархической структуре и свойствах графических объектов, уметь обращаться с указателями на них. Разумеется, не должна вызывать затруднение работа с числовыми массивами, строками, структурами, ячейками и массивами строк, структур и ячеек, а также использование конструкций встроенного языка программирования.

Элементы управления являются графическими объектами- потомками графического окна в иерархии объектов. Они могут быть созданы при помощи специальных функций низкоуровневой графики, но эффективнее использование визуальной среды GUIDE, которая позволяет создавать заготовку окна приложения, разместить на ней элементы управления, запрограммировать события и их взаимосвязь.

 Таблица 1.

Каждый интерфейсный элемент обладает заданным набором свойств, определяющих внешний вид и поведение компонента на стадии выполнения программы. В пакете MATLAB любому интерфейсному элементу всегда приписано 41 свойство (табл. 2).

Таблица 2.

Свойства интерфейсных компонентов

Создание приложения с графическим интерфейсом

1. Вход в визуальную среду GUIDE, основные настройки

- команда guide - переход в визуальную среду GUIDE;

- выбираем Blank GUI (Default) – пустое окно приложения без элементов управления, осей и меню;

- в меню Tools выбрать GUI Options, в списке Command-lime accessibility установить Callback (GUI becomes Curent Figure within Callbacks), включить переключатель Generate FIG-file and M-file – автоматическая генерация заготовок для подфункций обработки событий, использование окна приложения для графического вывода.

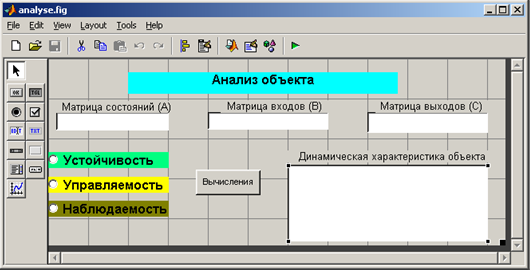
Рис. 6. Приложение "Analyse" в режиме редактирования.

3. Подфункцияобработкисобытий

analyse.m

function varargout = analyse(varargin)

% ANALYSE M-file for analyse.fig

% ANALYSE, by itself, creates a new ANALYSE or raises the existing

%singleton*.

%

%H = ANALYSE returns the handle to a new ANALYSE or the handle to

%the existing singleton*.

%

% ANALYSE("CALLBACK",hObject,eventData,handles,...) calls the local

% function named CALLBACK in ANALYSE.M with the given input arguments.

%

%ANALYSE("Property","Value",...) creates a new ANALYSE or raises the

%existing singleton*. Starting from the left, property value pairs are

%applied to the GUI before analyse_OpeningFunction gets called. An

%unrecognized property name or invalid value makes property application

%stop. All inputs are passed to analyse_OpeningFcn via varargin.

%

%*See GUI Options on GUIDE"s Tools menu. Choose "GUI allows only one

%instance to run (singleton)".

%

% See also: GUIDE, GUIDATA, GUIHANDLES

% Edit the above text to modify the response to help analyse 6

% Last Modified by GUIDE v2.5 21-Dec-2008 01:01:32

% Begin initialization code - DO NOT EDIT

gui_Singleton = 1;

gui_State = struct("gui_Name", mfilename, ...

"gui_Singleton", gui_Singleton, ...

"gui_OpeningFcn", @analyse_OpeningFcn, ...

"gui_OutputFcn", @analyse_OutputFcn, ...

"gui_LayoutFcn", [] , ...

"gui_Callback", []);

if nargin & isstr(varargin{1})

gui_State.gui_Callback = str2func(varargin{1});

end

if nargout

[varargout{1:nargout}] = gui_mainfcn(gui_State, varargin{:});

else

gui_mainfcn(gui_State, varargin{:});

end

% End initialization code - DO NOT EDIT

% --- Executes just before analyse is made visible.

function analyse_OpeningFcn(hObject, eventdata, handles, varargin)

% This function has no output args, see OutputFcn.

% hObject handle to figure

% eventdata reserved - to be defined in a future version of MATLAB

% handles structure with handles and user data (see GUIDATA)

% varargin command line arguments to analyse (see VARARGIN)

% Choose default command line output for analyse

handles.output = hObject;

% Update handles structure

guidata(hObject, handles);

% UIWAIT makes analyse wait for user response (see UIRESUME)

% uiwait(handles.figure1);

% --- Outputs from this function are returned to the command line.

function varargout = analyse_OutputFcn(hObject, eventdata, handles)

% varargout cell array for returning output args (see VARARGOUT);

% hObject handle to figure

% eventdata reserved - to be defined in a future version of MATLAB

% handles structure with handles and user data (see GUIDATA)

% Get default command line output from handles structure

varargout{1} = handles.output;

% --- Executes on button press in rbUst.

function rbUst_Callback(hObject, eventdata, handles)

% hObject handle to rbUst (see GCBO)

% eventdata reserved - to be defined in a future version of MATLAB

% handles structure with handles and user data (see GUIDATA)

% Hint: get(hObject,"Value") returns toggle state of rbUst

% Переключатель, событие которого обрабатывается, должен

% включиться, а остальные сброситься

set(handles.rbUst, "Value", 1)

set(handles.rbUpr, "Value", 0)

set(handles.rbNab, "Value", 0)

% --- Executes on button press in rbUpr.

function rbUpr_Callback(hObject, eventdata, handles)

% hObject handle to rbUpr (see GCBO)

% eventdata reserved - to be defined in a future version of MATLAB

% handles structure with handles and user data (see GUIDATA)

% Hint: get(hObject,"Value") returns toggle state of rbUpr

% Переключатель, событие которого обрабатывается, должен

% включиться, а остальные сброситься

set(handles.rbUst, "Value", 0)

set(handles.rbUpr, "Value", 1)

set(handles.rbNab, "Value", 0)

% --- Executes on button press in rbNab.

function rbNab_Callback(hObject, eventdata, handles)

% hObject handle to rbNab (see GCBO)

% eventdata reserved - to be defined in a future version of MATLAB

% handles structure with handles and user data (see GUIDATA)

% Hint: get(hObject,"Value") returns toggle state of rbNab 7

% Переключатель, событие которого обрабатывается, должен

% включиться, а остальные сброситься

set(handles.rbUst, "Value", 0)

set(handles.rbUpr, "Value", 0)

set(handles.rbNab, "Value", 1)

% --- Executes on button press in pbScore.

function pbScore_Callback(hObject, eventdata, handles)

% hObject handle to pbScore (see GCBO)

% eventdata reserved - to be defined in a future version of MATLAB

% handles structure with handles and user data (see GUIDATA)

data = getappdata(gcbf, "matrix");

% Проверка флага Устойчивость

if get(handles.rbUst,"Value")

% определение степени устойчивости

r=1-max(abs(eig(data.a)));

step_ust = r;

if step_ust==0

info="система нейтральна, т.к. степень устойчивости равна 0";

else

if step_ust < 0

info="система неустойчива, т.к. степень устойчивости меньше 0";

else

info="система устойчива, т.к. степень устойчивости в интервале (0;1)";

end

end

set(handles.etInfo, "String",sprintf("step_ust=%0.4g; %s",step_ust,info));

end

% Проверка флага Управляемость

if get(handles.rbUpr,"Value")

% определение управляемости

G=ctrb(data.a,data.b");

if rank(G)==size(data.a,1)

info="система управляема";

else

info="система не управляема";

end

set(handles.etInfo, "String",sprintf("%s",info));

end

% Проверка флага Наблюдаемость

if get(handles.rbNab,"Value")

% определение управляемости

H=obsv(data.a,data.c)";

if rank(H)==size(data.a,1)

info="система наблюдаема";

else

info="система не наблюдаема";

end

set(handles.etInfo, "String",sprintf("%s",info));

end

% --- Executes during object creation, after setting all properties.

function etInfo_CreateFcn(hObject, eventdata, handles)

% hObject handle to etInfo (see GCBO)

% eventdata reserved - to be defined in a future version of MATLAB

% handles empty - handles not created until after all CreateFcns called

% Hint: edit controls usually have a white background on Windows.

% See ISPC and COMPUTER.

if ispc

set(hObject,"BackgroundColor","white");

else

set(hObject,"BackgroundColor",get(0,"defaultUicontrolBackgroundColor"));

end

function etInfo_Callback(hObject, eventdata, handles)

% hObject handle to etInfo (see GCBO)

% eventdata reserved - to be defined in a future version of MATLAB

% handles structure with handles and user data (see GUIDATA)

% Hints: get(hObject,"String") returns contents of etInfo as text

% str2double(get(hObject,"String")) returns contents of etInfo as a double

% --- Executes during object creation, after setting all properties.

function etA_CreateFcn(hObject, eventdata, handles)

% hObject handle to etA (see GCBO)

% eventdata reserved - to be defined in a future version of MATLAB

% handles empty - handles not created until after all CreateFcns called

% Hint: edit controls usually have a white background on Windows.

% See ISPC and COMPUTER. 8

if ispc

set(hObject,"BackgroundColor","white");

else

set(hObject,"BackgroundColor",get(0,"defaultUicontrolBackgroundColor"));

end

function etA_Callback(hObject, eventdata, handles)

% hObject handle to etA (see GCBO)

% eventdata reserved - to be defined in a future version of MATLAB

% handles structure with handles and user data (see GUIDATA)

% Hints: get(hObject,"String") returns contents of etA as text

% str2double(get(hObject,"String")) returns contents of etA as a double

a = str2num(get(hObject, "String"));

data = getappdata(gcbf, "matrix");

data.a = a;

k=0;

% перевод вектора в матрицу

for i=1:sqrt(length(data.a))

for j=1:sqrt(length(data.a))

g(i,j)=data.a(k+1);

k=k+1;

end

end

data.a = g;

setappdata(gcbf, "matrix", data);

% --- Executes during object creation, after setting all properties.

function etB_CreateFcn(hObject, eventdata, handles)

% hObject handle to etB (see GCBO)

% eventdata reserved - to be defined in a future version of MATLAB

% handles empty - handles not created until after all CreateFcns called

% Hint: edit controls usually have a white background on Windows.

% See ISPC and COMPUTER.

if ispc

set(hObject,"BackgroundColor","white");

else

set(hObject,"BackgroundColor",get(0,"defaultUicontrolBackgroundColor"));

end

function etB_Callback(hObject, eventdata, handles)

% hObject handle to etB (see GCBO)

% eventdata reserved - to be defined in a future version of MATLAB

% handles structure with handles and user data (see GUIDATA)

% Hints: get(hObject,"String") returns contents of etB as text

% str2double(get(hObject,"String")) returns contents of etB as a double

b = str2num(get(hObject, "String"));

data = getappdata(gcbf, "matrix");

data.b = b;

setappdata(gcbf, "matrix", data);

% --- Executes during object creation, after setting all properties.

function etC_CreateFcn(hObject, eventdata, handles)

% hObject handle to etC (see GCBO)

% eventdata reserved - to be defined in a future version of MATLAB

% handles empty - handles not created until after all CreateFcns called

% Hint: edit controls usually have a white background on Windows.

% See ISPC and COMPUTER.

if ispc

set(hObject,"BackgroundColor","white");

else

set(hObject,"BackgroundColor",get(0,"defaultUicontrolBackgroundColor"));

end

function etC_Callback(hObject, eventdata, handles)

% hObject handle to etC (see GCBO)

% eventdata reserved - to be defined in a future version of MATLAB

% handles structure with handles and user data (see GUIDATA)

% Hints: get(hObject,"String") returns contents of etC as text

% str2double(get(hObject,"String")) returns contents of etC as a double 9

c = str2num(get(hObject, "String"));

data = getappdata(gcbf, "matrix");

data.c = c;

setappdata(gcbf, "matrix", data);

4. Результат работы приложения

В качестве тестовых матриц, описывающих объект, рассмотрим динамический маятник, где А=[0,1;-1,0], B=[1;1], C=[1,1] (рис. 7-9).

Рис. 7. Определение устойчивости.

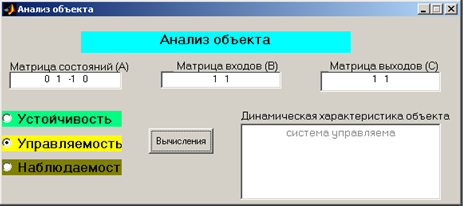
Рис. 8. Определение управляемости.

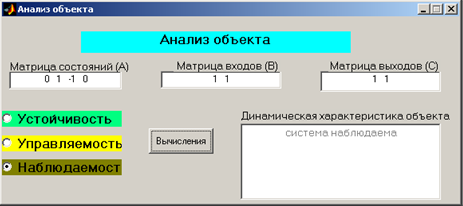
Рис. 9. Определение наблюдаемости.

5. Руководство пользователя

- в поле ввода для "Матрица состояния (А)", "Матрица входов (В)", "Матрица выходов (С)" необходим построчный ввод матриц, разделитель между элементами матриц "пробел";

- включить соответствующий переключатель;

- нажать кнопку "Вычисления", для получения динамической характеристики объекта, в поле "Динамическая характеристика объекта" появится характеристика объекта.

 2.1.

Разработать приложение с графическим интерфейсом для расчета интеграла функции и построения графика.

1. Создать новое приложение в среде GUIDE

>> guide

В диалоговом окне GUIDE Quick Start выбрать Blank GUI (пустое окно приложения)

 2. Создать заготовку приложения

Создать основные объекты: кнопки, надписи, поля ввода/вывода, координатные оси. Их размеры, положение и пр. в дальнейшем можно будет редактировать.

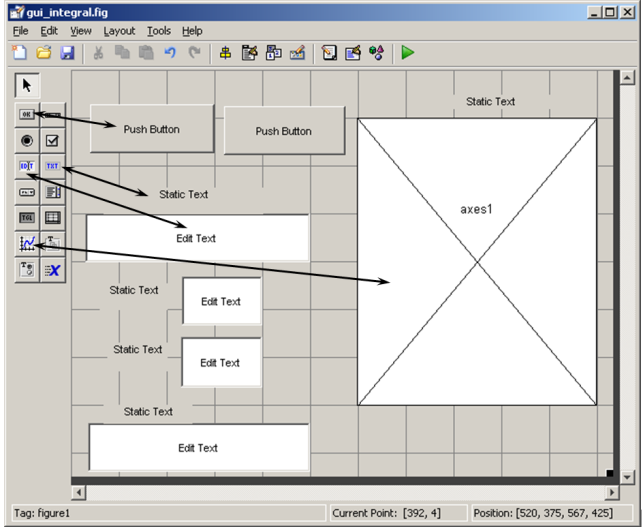
3. Задать имена и свойства объектов

В инспекторе свойств (Property Inspector) для каждого объекта задать следующие параметры:

4. Сохранить

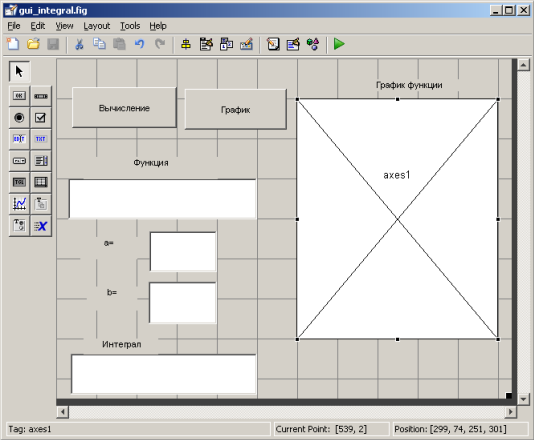
5. Алгоритм обработки событий

1. Ввод функции, используя поэлементные операции

При изменении функции добавить обратку события – очистка осей (поле для графика функции);

2. Ввод переделов интегрирования a и b

3. События, возникающие при нажатии кнопки «Вычисление» 4

3.1. Присвоить соответствующим переменным значения функции и пределов интегрирования.

% Переменной F присвоить значение свойства "String" объекта "FunctionName.

% Тип переменной "String" - string (строка, символьное выражение), поэтому тип переменной F -

% string

F=get(handles.FunctionName,"String");

% Переменной strStart присвоить значение свойства "String" объекта "Start"

strStart=get(handles.Start,"String");

% C помощью функции str2num("str") преобразем строку strStart в число

a=str2num(strStart);

% Можно записать в одну строку, передавая функции str2num() в качестве

% аргумента значение свойства "String" объекта "Start"

% a=str2num(get(handles.Start,"String"));

strLast=get(handles.Last,"String");

b=str2num(strLast);

% b=str2num(get(handles.Last,"String"));

3.2. Вычислить интеграл

% Вычисление интеграла методом парабол (квадратурная формула). Ограничение

% функции quad(F,a,b) - подинтегральная функция F должна содержать поэлементные операции

% (".*", "./", ".^"), тип данных F - string.

I=quad(F,a,b);

3.3. Записать результат расчета в поле «Интеграл»

% Переменной strI присваиваем преобразованное в строку значение интеграла I

strI=num2str(I);

% Задать свойству "String" объекта "Integral" значение strI

set(handles.Integral,"String",strI);

4. События, возникающие при нажатии кнопки «График»

4.1. Очистка осей

% Очистить графическое окно объекта "axes1"

axes(handles.axes1);

cla;

4.2. Присвоить соответствующим переменным значения функции и пределов интегрирования

% Для графического представления аналитически заданной функции

% воспользуемся фунцией ezplot (x,[min,max]), где x - символьное выражение

% или текстовая строка, содержащая аналитическое задание функциональной

% зависимости, [min,max] - область построения графика функции.

x=get(handles.FunctionName,"String");

min=str2num(get(handles.Start,"String")); 5

max=str2num(get(handles.Last,"String"));

4.3. Построить график функции, добавив подписи осей и сетку

ezplot (x,[min,max])

% Можно записать в одну строку

% ezplot (get(handles.FunctionName,"String"),[str2num(get(handles.Start,"String")),str2num(get(handles.Last,"String"))])

% Добавить подпись оси Y

ylabel("f(x)","FontSize",12);

% Добавить подпись оси X

xlabel("x","FontSize",12);

% Использовать основные лини сетки

set(handles.axes1, "XMinorGrid", "on", "YMinorGrid", "on");

% Использовать промужуточные лини сетки

set(handles.axes1, "XGrid", "on", "YGrid", "on", "GridLineStyle", "-");

6. Пример рабочего окна приложения

Численное интегрирование функции одной переменной

Обыкновенный определенный интеграл, у которого известна его

первообразная Fx, вычисляется по формуле Ньютона-Лейбница

I  Fa Fb. Поэтому для вычисления “простых”

определенных интегралов достаточно вычислить значения функции

Fx в точках x = a и x = b.

Применяют численный метод интегрирования, если невозможно

вычисление интеграла по формуле Ньютона — Лейбница или

первообразная функция является сложной для вычисления значений.

Определенный интеграл с пределами интегрирования a и b можно

   

b

a

I f x dx

трактовать как площадь фигуры, ограниченной ординатами a и b,

осью абсцисс x и графиком подынтегральной функции f x.

Суть метода численного интегрирования заключаются в замене

подынтегральной функции на более простую, т.е. интерполяции

функции f x на отрезке a,b подходящим полиномом,

интеграл которого можно вычислить аналитически.

Обычно отрезок a,b разбивается на n частей, к каждой из

которых применяется интерполяция функции и определяется

соответствующая формула интегрирования.

Метод прямоугольников

1) метод левых прямоугольников

1

0

( ) ( ),

b n

a i

f x dx h f a i h





    

где h b - a шаг интегрирования.

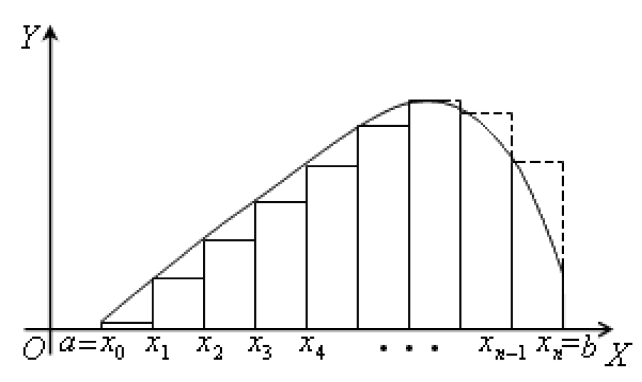
Рис. 1. Ступенчатая фигура, полученная по методу левых

Прямоугольников

Псевдокод алгоритма метода левых прямоугольников

ввод f (x), n, a, b

i = 0

S = 0

h = (b − a)/n

пока i ≤ n − 1 делать

x = a + i∙h

S = S + f (x)·h

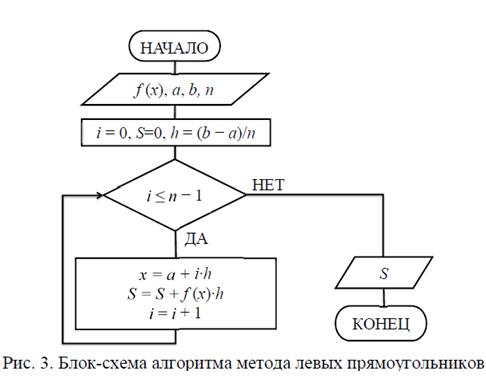
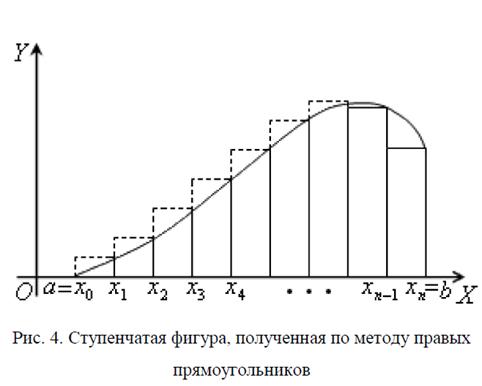
2) метод правых прямоугольников

1

( ) ( ),

b n

a i

f x dx h f a i h

( ) ( ( 0,5) )

b n

a i

f x dx h f a i h





function I=inegral_R(func,a,b,n)

% Функция возвращает значение определенного

интеграла, вычисленного методом

% прямоугольников.

% Входные аргументы:

% func - переменная, представляет функцию в виде

строки

% a - начало промежутка интегрирования

% b - конец промежутка интегрирования

% n - число узлов (число отрезков, разделяющих

интервал [a,b])

% Выходные аргументы:

% I - значение определенного интеграла функции на

отрезке [a,b]

% Чтобы задать свою функцию, используем функцию

inline, см. ниже или help inline

f=inline(func);

% теперь переменная f является зависимостью f(x),

записанной в переменной func.

%%%

I=0;

% h - шаг интегрирования

h=(b-a)/n;

for i=0:n-1

% х - высота прямоугольника

x=a+h*(i+0.5);

% f(x)*h - площадь прямоугольника

% I - сумма площадей прямоугольников

I=I+f(x)*h;

End

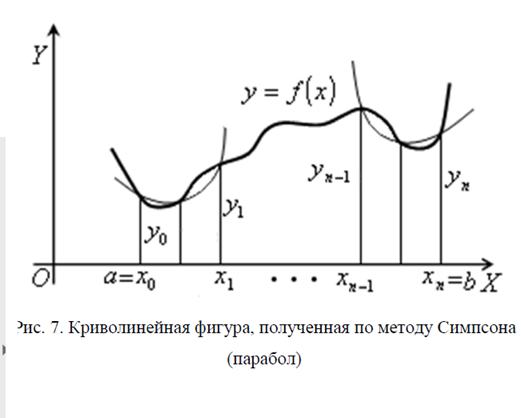
Метод Симпсона (парабол)

где xi  a  i  h

       1

1/2 1

0

( ) 4 ,

6

b n

i i i

a i

f x dx h f x f x f x

function I=inegral_P(func,a,b,n)

% Функция возвращает значение определенного

интеграла, вычисленного методом

% Симпсона (парабол).

% Входные аргументы:

% func - переменная, представляет функцию в виде

строки

% a - начало промежутка интегрирования

% b - конец промежутка интегрирования

% n - число узлов (число отрезков, разделяющих

интервал [a,b])

% Выходные аргументы:

% I - значение определенного интеграла функции на

отрезке [a,b]

% Чтобы задать свою функцию, используем функцию

inline, см. ниже или help inline

f=inline(func);

% теперь переменная f является зависимостью f(x),

записанной в переменной func.

%%%

I=0;

% h - шаг интегрирования

h=(b-a)/n;

for i=0:n-1

% x1 - начало i-го отрезка

x1=a+h*i;

% x2 - конец i-го отрезка

x2=x1+h;

% x12 - середина i-го отрезка

x12=(x1+x2)/2;

% (f(x1)+4*f(x12)+f(x2))*h/6 - площадь

параболы

% I - сумма площадей парабол

22

I=I+(f(x1)+4*f(x12)+f(x2))*h/6;

End