Разновидности задач оптимизации»

Курская академия государственной и муниципальной службы

Кафедра информационной и техносферной безопасности

РЕФЕРАТ

по дисциплине « Методы оптимальных решений»

по теме « Разновидности задач оптимизации»

                                                              Выполнила: студентка 2 курса

                                                              специальности «Экономика»

                                                              Меркулова М. П.

                                                              Проверил: к.ф.м.н, доцент

                                                              Погосян С. Л.

                                  КУРСК-2012

                      Содержание

Введение……………………………………………………...............3

1.    Постановка задач оптимизации…………………….............4

1.1.        Основные понятия………………………………….......4

1.2.        Два основных аспекта проблемы оптимизации…….4

    2. Классификация задач оптимизации………………………...7

3. Оптимизационные задачи …………………………………....9

        3.1. Обозначения в задачах……………………………………9

        3.2. Задача наилучшего приближения………………………9

          3.3. Задача Штейнера…………………………………………10

          3.4. Задача о рационе………………………………………….11

        3.5. Транспортная задача…………………………………….12

        3.6. Задача о распределении ресурсов……………………....13

Заключение………………………………………………………….14

Список используемой литературы………………………………15

                           Введение

Задача оптимизации — в математике, информатике и исследовании операций задача нахождения экстремума (минимума или максимума) целевой функции в некоторой области конечномерного векторного пространства, ограниченной набором линейных и/или нелинейных равенств и/или неравенств.

В процессе проектирования ставится обычно задача определения наилучших, в некотором смысле, структуры или значений параметров объектов. Такая задача называется оптимизационной. Если оптимизация связана с расчетом оптимальных значений параметров при заданной структуре объекта, то она называется параметрической оптимизацией. Задача выбора оптимальной структуры является структурной оптимизацией.

Решения задачи оптимизации состоит из нескольких этапов:

– создание модели задачи оптимизации;

– поиск решения задачи оптимизации;

– анализ найденного решения задачи оптимизации.

Общая запись задач оптимизации задаёт большое разнообразие их классов. От класса задачи зависит подбор метода (эффективность её решения). Классификацию задач определяют: целевая функция и допустимая область (задаётся системой неравенств и равенств или более сложным алгоритмом).

Методы оптимизации классифицируют в соответствии с задачами оптимизации:

§     Локальные методы: сходятся к какому-нибудь локальному экстремуму целевой функции. В случае унимодальной целевой функции, этот экстремум единственен, и будет глобальным максимумом/минимумом.

§     Глобальные методы: имеют дело с многоэкстремальными целевыми функциями. При глобальном поиске основной задачей является выявление тенденций глобального поведения целевой функции.

Цель данной работы рассмотреть:

 1. Постановку задач оптимизации;

 2. Какие виды задач оптимизации существуют.

1.    Постановка задачи оптимизации

1.1.      Основные понятия

Под оптимальным понимают такое проектирование, цель которого состоит в создании технического объекта (ТО), не только выполняющего заданные функции, но и отвечающего некоторым заранее установленным критериям качества.

Поиск рационального технического решения при выбранном физическом принципе действия осуществляется методом структурного синтеза. Определение оптимальных значений параметров элементов технической системы известной структуры - задача параметрического синтеза или параметрической оптимизации.

Постановка задачи оптимизации имеет содержательный смысл только в том случае, когда появляется необходимость выбора одного из конкурирующих вариантов, полученных при ограниченности ресурсов. Техническое проектирование всегда ведется в условиях жестких ограничений на материальные, энергетические, временные и прочие виды ресурсов. Вместе с тем средства САПР позволяют выполнить разработку нескольких альтернативных вариантов. Поэтому окончательный выбор технического объекта (принятие решения) необходимо проводить на основании установленных критериев. Выбор критерия является одним из важных этапов постановки задачи оптимизации, так как все последующие действия направлены на поиск объекта, наиболее близкого к оптимальному по выбранному критерию.

В основе построения правила предпочтения лежит целевая функция, количественно выражающая качество объекта и потому называемая также функцией качества или критерием оптимальности. Формирование целевой функции всегда выполняется с учетом различных выходных параметров проектируемого устройства. В зависимости от содержательного смысла этих параметров и выбранного способа их сочетания в целевой функции качество объекта будет тем выше, чем больше ее значение (максимизация) или чем меньше ее значение (минимизация).

1.2.      Два основных аспекта проблемы оптимизации

Проблема оптимизации имеет два основных аспекта:

1) нужно поставить задачу, формализовав понятие "оптимальный";

2) нужно решить задачу, уже имеющую математическую формулировку.

Математическая модель (ММ) оптимального проектирования технического объекта представляет собой формализованное описание критерия качества, условий, обеспечивающих выполнение заданных функций объектом, требований предъявляемых к отдельным параметрам объекта и др.

Именно в формировании ММ заключается постановка задачи оптимального проектирования ТО, которой предшествует определение цели и соответствующего критерия оптимизации. Например, при проектировании ТО цели оптимизации могут состоять в обеспечении: его минимальной массы; максимального КПД; минимальных размеров; максимальной надежности; минимальной стоимости изготовления; минимального количества расходуемого материала, топлива; максимальной грузоподъемности, производительности и др.

Каждой из перечисленных целей оптимального проектирования соответствует свой критерий оптимальности (масса, КПД, размеры). Критерии оптимальности выражают целевыми функциями f(x),представляющими собой математические зависимости их значений от параметров проектируемого технического объекта.

На первом этапе разработки математической модели оптимального проектирования выявляют параметры объекта, влияющие на критерий оптимальности, и определяют вид функциональной зависимости этих параметров. Далее определяют параметрические, дискретизирующие и функциональные ограничения, накладываемые на параметры технического объекта, для обеспечения им заданных функций.

Параметрическими называют ограничения вида:

x_i"≤x_i  ≤x_i",

где  x_i - i-тый параметр технического объекта; x_i" и x_i" -соответственно min и max допустимые значения i-го параметра.

Дискретизирующие ограничения имеют вид:

x_j ={x_j1,x_j2,...,x_jm},

где x_j- j-тый параметр ТО; x_jk- допустимые значения j-го параметра (k=1,2,..m).

Эти ограничения накладывают на значение параметров либо в связи с их физической сущностью (например, число зубьев передачи), либо в связи с требованиями ГОСТов, отраслевых стандартов.

Функциональные ограничения, накладываемые на параметры объектов, представляют собой условия связи их значений. Эти ограничения имеют вид:

g_i(x)  ≤ 0;g_j(x)=0;g_k(x)<0.

Функциональными ограничениями при оптимальном проектировании технических объектов могут быть условия: прочности; жесткости; устойчивости; герметичности; срока службы. Эти условия обеспечивают желаемые значения тех или иных технических характеристик и экономических показателей. 

Определение ограничений является чрезвычайно ответственным этапом в процессе постановки и решения задач оптимального проектирования. Неучет каких-либо ограничений может привести к таким нежелательным эффектам, как преждевременный выход из строя ТО или низкое значение технико-экономических показателей и других характеристик объекта. Вместе с тем, избыточные ограничения повышают сложность модели, используемых алгоритмов и методов решения задач, а также увеличивают затраты машинного времени.

При постановке задач оптимального проектирования необходим анализ совместимости параметрических, дискретизирующих и функциональных ограничений. При этом, если окажется, что допустимое подпространство проектирования Д является пустым множеством, то следует пересмотреть ограничения и выявить противоречащие. Поиск оптимальных решений возможен, еслиД содержит хотя бы две точки. Таким образом, задачу оптимального проектирования формулируют следующим образом. Найти такое x*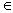 , для которого f(x*)=minf(x),x 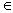Д. Найденное в результате решения задачи x* называют оптимальным решением, а f(x*)- оптимальным значением критерия оптимальности.

2. Классификация задач оптимизации

Принято различать задачи статической оптимизации для процессов, протекающих в установившихся режимах, и задачи динамической оптимизации.

В первом случае решаются вопросы создания и реализации оптимальной модели процесса, во втором- задачи создания и реализации системы оптимального управления процессом при неустановившихся режимах эксплуатации.

Если требуется определить экстремум целевой функции без задания условий на какие-либо другие величины, то такая оптимизация называется безусловной. Такие критерии обычно используются при решении частных задач оптимизации (например, определение максимальной концентрации целевого продукта, оптимального времени пребывания реакционной смеси в аппарате и т.п.).

Если необходимо установить экстремум целевой функции при некоторых условиях, которые накладываются на ряд других величин (например, определение максимальной производительности при заданной себестоимости, определение оптимальной температуры при ограничениях по термостойкости катализатора и др.), то такая оптимизация называется условной.

Процедура решения задачи оптимизации обязательно включает, помимо выбора управляющих параметров, еще и установление ограничений на эти параметры (термостойкость, взрывобезопасность, мощность перекачивающих устройств).

Ограничения могут накладываться как по технологическим, так и по экономическим соображениям.

В зависимости от управляющих параметров различают следующие задачи:

·        оптимизация при одной управляющей переменной- одномерная оптимизация,

·        оптимизация при нескольких  управляющих переменных – многомерная оптимизация,

·        оптимизация при неопределённости  данных,

·        оптимизация с непрерывными дискретными и смешанным типом значений управляющих воздействий.

В зависимости от критерия оптимизации различают:

·        с одним критерием оптимизации- критерий оптимальности  единственный.

·        со многими критериями. Для решения задач со многими критериями  используются специальные методы оптимизации.

Один из классификационных признаков делит оптимизационные задачи на два класса: задачи безусловной оптимизации и задачи условной оптимизации. Первые из них характеризуются тем, что минимум функции f: R^m ® R ищется на всем пространстве:

f(x) ® min,   x Î Rm.

(1)

В задачах же второго класса поиск минимума идет на некотором собственном подмножестве W пространства R^m:

f(x) ® min,   x Î W.

(2)

Множество W часто выделяется ограничениями типа равенств

g0(x) = Q,

(3)

где g₀: R^m ® R^k, и/или ограничениями типа неравенств

g1(x) £ Q,

(4)

где g₁: R^m ® R^l.

Другой классификационный признак задач оптимизации — свойства функций f и множеств W. Например задачи (1) и (2) называются линейными (часто говорят о задачах линейного программирования), если функция f — аффинная, а множество W — многогранное (множество W называется многогранным, если оно выделяется ограничениями вида (3) и (4) с аффинными функциями g₀ и g₁).

Задача. Докажите, что линейная задача безусловной оптимизации (1) имеет решение (причем обязательно неединственное) в том и только том случае, если f(x) º const.

Если функции f, g₀ и g₁ квадратичные, то говорят о задачах квадратичного программирования или о квадратичных задачах оптимизации (условных или безусловных). Если эти функции выпуклые, то говорят о задачах выпуклого программирования (если множество W задается каким-либо другим образом, а не только ограничениями типа (4) и (5), то в задачах выпуклого программирования требуют его выпуклость). Наконец, в общем случае говорят о задачах нелинейного программирования. В таких задачах обычно предполагается гладкость фигурирующих в них функций. Именно этим задачам в данном пособии будет уделено основное внимание.

        3. Оптимизационные задачи

3.1. Обозначения в задачах

Всюду ниже R — множество вещественных, N — натуральных, а C — комплексных чисел. С самого начала мы будем использовать векторные обозначения. Всегда через R^m обозначается m-мерное вещественное линейное пространство. При этом мы всегда считаем, что в R^m фиксирован базис и отождествляем R^m с арифметическим m-мерным пространством (пространством упорядоченных наборовm вещественных чисел). Буква Q будет обозначать нуль пространства R^m. Индекс внизу всегда обозначает координату вектора, например, x_i — это i-ая координата вектора x. Последовательности мы обычно будем обозначать индексом вверху: {xⁿ}.

Через (· ,·) обозначается каноническое скалярное произведение в Rm: (x, y) = åmi=1xiyi. Если не оговорено противное,, порожденную скалярным произведением: || · || = (åmi=1xi2)1/2.

Обозначение B(x₀, r) закреплено для шара в пространстве R^m с центром в x₀ радиуса r: B(x₀, r) = {x Î R^m: ||x - x₀|| £ r}.

Если A = {a_ij}^n, m_i=1, j=1  —n×m-матрица, то через A также обозначается и линейный оператор из Rⁿ в R^m, задаваемый этой матрицей.

Для двух векторов x, y Î R^m мы будем писать x £ y, если x_i £ y_i при всех i = 1, ..., m; здесь x_i и y_i — i-е координаты векторов x и y, соответственно.

Мы будем различать обозначение f: X ® Y отображения, действующего из множества X во множество Y, и обозначениеf: x ® y (или x ® f(x)) отображения, переводящего точку x в точку f(x), а также обозначение f отображения и обозначение f(x) значения отображения f в точке x.

3.2. Задача наилучшего приближения

Если рассматривать систему n линейных уравнений с m неизвестными

Ax = b

в случае, когда она переопределена, то иногда оказывается естественной задача о нахождении вектора x, который "удовлетворяет этой системе наилучшим образом", т. е. из всех "не решений" является лучшим. Например, бывает полезной задача о нахождении вектора x, для которого разность правой и левой частей системы (невязка) минимальна, т. е. минимальна функция

f(x) = ||Ax - b||.

(1)

Эту задачу символически записывают в виде

f(x) ® min

Норму в (1) можно брать разную. Например, если взята евклидова норма, то получается задача о наилучшем квадратичном приближении

æ è n å i = 1 ê ê m å j = 1 aijxj - bi ê ê 2 ö ø 1/2  ® min,

или, что эквивалентно,

n å i = 1 êê êê m å j = 1 aijxj - bi êê êê 2  ® min,

Геометрически эта задача интерпретируется как задача о нахождении на гиперплоскости A(R^m) в пространстве Rⁿ точки, ближайшей к точке b = (b₁, ..., b_n).

 3.3. Задача Штейнера

Классическая задача Штейнера формулируется так: требуется найти точку x Î R^m, сумма расстояний от которой до заданных точекx¹, ..., xⁿ Î R^m минимальна. Эта задача типично оптимизационная:

f(x) =(def)  n å i = 1 ||x - xi|| ® min

Задача  1.1. Найдите решение задачи Штейнера при m = 2, n = 3.

Приведенные выше задачи представляют собой задачи безусловной оптимизации — на искомое решение не налагается никаких дополнительных условий, кроме того, что оно должно доставлять минимум некоторой функции (другими словами, минимум функции ищется на всем пространстве — области определения функции). Чаще встречаются задачи условной оптимизации, примеры которых мы приводим ниже.

3.4. Задача о рационе

Пусть имеется  n  различных пищевых продуктов, содержащих m различных питательных веществ. Обозначим через a_ij содержание (долю) j-го питательного вещества в i-ом продукте, через b_j — суточную потребность организма в j-ом питательном веществе, черезc_i — стоимость единицы i-го продукта. Требуется составить суточный рацион питания минимальной стоимости, удовлетворяющий потребность во всех питательных веществах. Если обозначить через x_i суточное потребление i-го продукта, то эта задача может быть формализована следующим образом. Нужно минимизировать функцию

f(x1, ..., xn) =  n å i = 1 cixi   (стоимость рациона)

при условиях

n å i = 1 aijxi ³ bj,   j = 1, ..., m

(рацион должен содержать не менее суточной
потребности в каждом из питательных веществ).

Очевидно, также следует требовать, чтобы

xi ³ 0,   i = 1, ..., n.

В векторных обозначениях задача о рационе может быть записана так: минимизировать функцию

f(x) = (c, x),

где c = (c₁, ..., c_n) Î Rⁿ; эту задачу, как обычно, мы записываем в виде

(c, x) ® min,

при ограничениях

Ax ³ b,

x ³ Q.

В них первое неравенство связывает два вектора Ax и b из R^m, а второе – два вектора x и Q из Rⁿ.

По легенде одним из первых приложений задачи о рационе к реальной жизни была попытка рассчитать оптимальный рацион для американской армии во время второй мировой войны. Результат был неожиданным: солдат в день должен выпивать литр уксуса и съежать килограм бобов (цифры и продукты условные).

3.5. Транспортная задача

Эта задача — классическая задача линейного программирования. К ней сводятся многие оптимизационные задачи. Формулируется она так. На m складах находится груз, который нужно развезти n потребителям. Пусть a_i (i = 1, ..., n) — количество груза на i-ом складе, аb_j (j = 1, ..., m) — потребность в грузе j-го потребителя, c_ij — стоимость перевозки единицы груза с i-го склада j-му потребителю. Требуется минимизировать стоимость перевозок. Если обозначить через x_ij объем перевозок с i-го склада j-му потребителю, то транспортная задача формализуется так:

n å i = 1 m å j = 1 cijxij ® min,

n å i = 1 xij = bj,   j = 1, ..., m

(все потребители должны быть удовлетворены),

m å j = 1 xij = ai,   i = 1, ..., n

(весь груз должен быть доставлен потребителю),

xij ³ 0

(нельзя перевозить груз от потребителя на склад).

Задача  1.2. Запишите транспортную задачу в векторном виде.

Это были примеры линейных задач условной оптимизации. Приведем один пример нелинейной задачи.

3.6. Задачи о распределении ресурсов

Общий смысл таких задач — распределить ограниченный ресурс между потребителями оптимальным образом. Рассмотрим простейший пример — задачу о режиме работы энергосистемы. Пусть m электростанций питают одну нагрузку мощности p. Обозначим через x_j активную мощность, генерируемую j-ой электростанцией. Техническими условиями определяются возможный минимум m_j и максимум M_j вырабатываемой j-ой электростанцией мощности. Допустим затраты на генерацию мощности x на j-ой электростанции равны e_j(x). Требуется сгенерировать требуемую мощность p при минимальных затратах. В наших обозначениях

f(x) =(def)  m å j = 1 ej(xj) ® min,

m å j = 1 xj = p,

mj £ xj £ Mj,   j = 1, ..., m.

Если обозначить åmj=1ej(xj)через f(x), åmj=1xj- p через g(x), а {x Î Rm: m £ x £ M} через W, то эта задача переписывается так

f(x) ® min, g(x) = 0, x Î W.

Заключение

Развитие современного общества характеризуется повышением технического уровня, усложнением организационной структуры производства, управления войсками, углублением общественного разделения труда, предъявлением высоких требований к методам планирования хозяйственного и военного руководства. В этих условиях только научный подход к руководству хозяйственной жизнью общества позволит обеспечить высокие темпы развития народного хозяйства. Научного подхода требует и решение тактических и стратегических задач, руководство военными операциями.

В настоящее время новейшие достижения математики и современной вычислительной техники находят все более широкое применение как в экономических исследованиях и планировании, так и в решении военных тактических задач. Этому способствует развитие таких разделов математики как математическое программирование, теория игр, теория массового обслуживания, а также бурное развитие быстродействующей электронно-вычислительной техники. Уже накоплен большой опыт постановки и решения экономических и тактических задач с помощью математических методов. Особенно успешно развиваются методы оптимального управления.

Общая запись задач оптимизации задаёт большое разнообразие их классов. От класса задачи зависит подбор метода (эффективность её решения). Классификацию задач определяют: целевая функция и допустимая область (задаётся системой неравенств и равенств или более сложным алгоритмом). По виду целевой функции и допустимого множества, задачи оптимизации и методы их решения можно разделить на следующие классы:

·                     Задачи оптимизации, в которых целевая функция 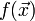 и ограничения  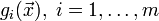являются линейными функциями, разрешаются так называемыми методами линейного программирования.

·                     В противном случае имеют дело с задачей нелинейного программирования и применяют соответствующие методы. В свою очередь из них выделяют две частные задачи:

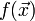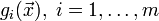o         если  и  — выпуклые функции, то такую задачу называют задачей выпуклого программирования;

o         если 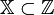, то имеют дело с задачей целочисленного (дискретного) программирования.

По требованиям к гладкости и наличию у целевой функции частных производных, их также можно разделить на:

·                     прямые методы, требующие только вычислений целевой функции в точках приближений;

·                     методы первого порядка: требуют вычисления первых частных производных функции;

·                     методы второго порядка: требуют вычисления вторых частных производных, то есть гессиана целевой функции.

Список используемой литературы

1.     Методы оптимальных решений. Токарев В. В.

2.     Методы оптимальных решений- учебное пособие для вузов.

3.     А.Г.Трифонов. "Постановка задачи оптимизации и численные методы ее решения".

4.     Классификация задач оптимизации.

http://mm.lti-gti.ru/works_lectures/5.htm

5.     Задачи оптимизации.

                    http://www-sbras.nsc.ru/rus/textbooks/akhmerov/mo/1.html

6.     Оптимизация.

      http://ru.wikipedia.org

7.     Постановка задачи оптимизации.

                     http://www.rae.ru/monographs/57-2322