Размещения, перестановки, сочетания

Министерство образования Тверской области

Государственное бюджетное профессиональное образовательное учреждение

«Бологовский колледж»

Реферат

Тема « Размещения, перестановки, сочетания»

Работу выполнила

студентка  22 группы

Козлова Софья

г.Бологое

В комбинаторике изучают вопросы о том, сколько комбинаций определенного типа можно составить из данных предметов (элементов).

Рождение комбинаторики как раздела математики связано с трудами Б. Паскаля и П. Ферма по теории азартных игр. Большой вклад в развитие комбинаторных методов внесли Г.В. Лейбниц, Я. Бернулли и Л. Эйлер.

Определение. Размещениями множества из  различных элементов по  элементов  называются комбинации, которые составлены из данных  элементов по  элементов и отличаются либо самими элементами, либо порядком элементов.

Число всех размещений множества из  элементов по  элементов обозначается через  (от начальной буквы французского слова “arrangement”, что означает размещение), где  и .

Пример 1. Сколькими способами можно составить флаг, состоящий из трех горизонтальных полос различных цветов, если имеется материал пяти цветов?

Решение. Искомое число трехполосных флагов:

                                      

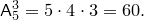
Пример 2.

Сколько трехзначных чисел можно составить из 4 цифр: 1, 2, 3, 4?

Решение.

Перечислим с помощью схемы все возможные числа:

Видим, что всего данных чисел 4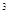 = 64, где 4 — количество элементов исходного множества, а 3 — число выбранных элементов.

Пример 3.

Сколько трехэлементных подмножеств, различающихся хотя бы одним элементом друг от друга и без учета порядка в подмножестве, можно составить из 4 цифр: 1, 2, 3, 4?

Решение.

Перечислим все полученные подмножества:

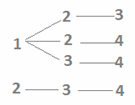
 (1, 2, 3), (1, 2, 4), (1, 3, 4), (2, 3, 4).

Видим, что всего получилось 4 подмножества.

Определение. Перестановкой множества из  элементов называется расположение элементов в определенном порядке.

Число всех перестановок из  элементов обозначается  (от начальной буквы французского слова “permutation”, что значит “перестановка”, “перемещение”)

Задача 1.Сколькими способами можно расставить 8 ладей на шахматной доске так, чтобы они не били друг друга?

Решение. Искомое число расстановки 8 ладей

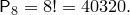
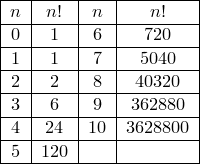
Задача 2

Сколькими способами можно рассадить 5 человек за столом?

Решение: используем формулу количества перестановок:

 

Ответ: 120 способами.

Ответ: 1365 способами

Определение. Сочетаниями из  различных элементов по  элементов называются комбинации, которые составлены из данных  элементов по  элементов и отличаются хотя бы одним элементом (иначе говоря, -элементные подмножества данного множества из  элементов).

Как видим, в сочетаниях в отличие от размещений не учитывается порядок элементов. Число всех сочетаний из  элементов по  элементов в каждом обозначается  (от начальной буквы французского слова “combinasion”, что значит “сочетание”).

 

Задача 1.

Сколькими способами из класса, в котором учатся 30 школьников, можно выбрать капитана команды для математических соревнований и его заместителя?

Решение.

1-й способ: на роль капитана может быть выбран любой из 30 учащихся, а его заместитель — любой из 29 оставшихся учеников. Таким образом, получаем 30 · 29 = 870 способов.

2-й способ: порядок важен, тогда по формуле числа размещений имеем

 способов.

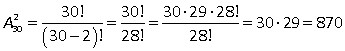
Ответ: 870.

Пример 2.

Сколькими способами из класса, в котором учатся 30 школьников, можно выбрать двоих для участия в математической олимпиаде?

Решение.

1-й способ: нам не важно, кто капитан, а кто заместитель, нам нужны всего лишь два участника, поэтому получаем, что у нас каждая пара учащихся в произведении повторяется два раза. Поэтому ответом для второй задачи будет (30 · 29) : 2 = 435.

2-й способ: без учета порядка применим формулу числа сочетаний

.

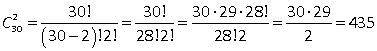
Ответ: 435.

Пример 3.

Сколькими способами можно построить пятерых человек в шеренгу?

Решение.

По формуле числа перестановок имеем Р₅ = 5 · 4 · 3 · 2 · 1 = 120.

Ответ: 120.

Задачи:

1.      Сколько четырехзначных чисел можно составить из 9 цифр: 1, 2, 3, 4, 5, 6, 7, 8, 9?

2.      В чемпионате участвует 12 команд. Сколькими различными способами могут быть распределены три различные медали?

3.      В семье 6 человек. За столом 6 стульев. В семье решили каждый вечер рассаживаться на эти 6 стульев по-новому. Сколько дней члены семьи смогут делать это без повторений?