1. Расчет электрических цепей постоянного тока
 |






 R4
R4

 IIII E1 I4
IIII E1 I4
 I3 I5
I3 I5
 D
I6
D
I6

 R5 R6
R5 R6

 III
III


 R2 I2
R2 I2
 A
C
A
C
E2
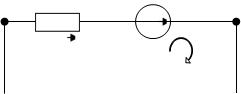
Рисунок 1.1 – Схема электрической цепи постоянного тока
Таблица1.1-Исходные данные
|
Е1,В |
Е2,В |
R1,Ом |
R2,Ом |
R3,Ом |
R4,Ом |
R5,Ом |
R6,Ом |
r1, Ом |
r2, Ом |
|
20 |
30 |
54 |
43 |
32 |
26 |
51 |
15 |
2 |
2 |
1.1 Расчет электрических цепей постоянного тока методом узловых и контурных токов
1.2 Расчет электрических цепей постоянного тока методом контурных токов
1.3 Расчет электрических цепей методом узлового напряжения
1.1 Расчет электрических цепей постоянного тока методом узловых и контурных токов
Пользуясь рисунком 1.1 и данными таблицы 1.1, делаем расчет электрической цепи методом узловых и контурных токов. Данный метод основан на применении первого закона и второго закона Кирхгофа. Направление токов в ветвях задаем произвольно. Составляем систему уравнений (количество уравнений должно ровняться числу ветвей в цепи), так как в цепи 6 ветвей, то и уравнений будет 6.
Сначала составляем уравнения по первому закону Кирхгофа: Алгебраическая сумма токов в узле равна нулю.
∑I=0 (1)
Где I ток в ветви (А).
Количество уравнений равно количеству узлов минус один, так как у нас 3 узла то уравнений будет 2:
Для узла A: 0=I3 +I4+I5
Для узла D: 0=I1-I2-I3
Оставшиеся 3-и уравнения составляем по второму закону Кирхгофа:
В контуре электрической цепи алгебраическая сумма ЭДС равна алгебраической сумме падений напряжения в этом контуре:
∑E=∑IR (2)
гдеE – ЭДС (В).
R – сопротивление (Ом).
I - ток в ветви (А).
Контур ADCA: E1=I1 (R1+r1)+I2
(R1+r1)+I2 R3+R4)
R3+R4)
Контур BDCB: -E2=-I2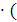 R3+R4)+I3
R3+R4)+I3 R5+I4
R5+I4 (R3+R4)
(R3+R4)
Контур DBAD: E2= I4 (R2+r02)-I5
(R2+r02)-I5 R6
R6
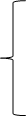 |
0=I3 +I4+I5
0=I1-I2-I3
E1=I1 (R1+r1)+I2
(R1+r1)+I2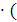 R3+R4)
R3+R4)
-E2=-I2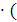 R3+R4)+I3
R3+R4)+I3 R5+I4
R5+I4 (R3+R4)
(R3+R4)
E2= I4 (R2+r02)-I5
(R2+r02)-I5 R6
R6
Таблица 2. Данные для метода Крамера
|
I1 |
I2 |
I3 |
I4 |
I5 |
E |
|
0 |
0 |
1 |
1 |
1 |
0 |
|
-1 |
-1 |
-1 |
0 |
0 |
0 |
|
56 |
58 |
0 |
0 |
0 |
20 |
|
0 |
-58 |
51 |
-45 |
0 |
-30 |
|
0 |
0 |
0 |
45 |
-15 |
30 |
Решение системы находим по следующим формулам
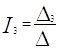 |
||||||||
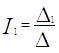 |
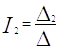 |
|||||||
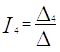 |
 |
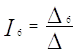
|
0 |
0 |
1 |
1 |
1 |
||||
|
|
-1 |
-1 |
-1 |
0 |
0 |
|||
|
= |
56 |
58 |
0 |
0 |
0 |
= |
187410 |
|
|
0 |
-58 |
51 |
-45 |
0 |
||||
|
0 |
0 |
0 |
45 |
-15 |
||||
|
0 |
0 |
1 |
1 |
1 |
||||
|
|
0 |
-1 |
-1 |
0 |
0 |
|||
|
= |
20 |
58 |
0 |
0 |
0 |
= |
118200 |
|
|
-30 |
-58 |
51 |
-45 |
0 |
||||
|
30 |
0 |
0 |
45 |
-15 |
||||
|
0 |
0 |
1 |
1 |
1 |
||||
|
|
-1 |
0 |
-1 |
0 |
0 |
|||
|
= |
56 |
20 |
0 |
0 |
0 |
= |
-49500 |
|
|
0 |
-30 |
51 |
-45 |
0 |
||||
|
0 |
30 |
0 |
45 |
-15 |
||||
|
0 |
0 |
0 |
1 |
1 |
||||
|
|
-1 |
-1 |
0 |
0 |
0 |
|||
|
= |
56 |
58 |
20 |
0 |
0 |
= |
-68700 |
|
|
0 |
-58 |
-30 |
-45 |
0 |
||||
|
0 |
0 |
30 |
45 |
-15 |
||||
|
0 |
0 |
1 |
0 |
1 |
||||
|
|
-1 |
-1 |
-1 |
0 |
0 |
|||
|
= |
56 |
58 |
0 |
20 |
0 |
= |
110880 |
|
|
0 |
-58 |
51 |
-30 |
0 |
||||
|
0 |
0 |
0 |
30 |
-15 |
||||
|
0 |
0 |
1 |
1 |
0 |
||||
|
|
-1 |
-1 |
-1 |
0 |
0 |
|||
|
= |
56 |
58 |
0 |
0 |
20 |
= |
-42180 |
|
|
0 |
-58 |
51 |
-45 |
-30 |
||||
|
0 |
0 |
0 |
45 |
30 |
После решения методом Крамера получили следующие токи:
|
I1 = |
0,1904A |
|
I2 = |
0,1610A |
|
I3 = |
0,0295A |
|
I4 = |
0,4926A |
|
I5 = |
-0,5221A |
1.2 Расчет электрической цепи постоянного тока методом контурных токов
Метод контурных токов основан на использовании второго закона Кирхгофа. Это позволяет уменьшить число уравнений в системе на n-1.
Достигается это разделением схемы (см. рисунок 1) на независимые контуры и введением для каждого контура своего тока, являющегося расчетной величиной.
Для независимых контуров задаём направление контурных токов.
Составляем систему уравнений (количество уравнений равно количеству независимых контуров):
Уравнения составляем по правилу: левая часть представляет собой алгебраическую сумму ЭДС, входящих в контур. Правая часть уравнения представляет собой сумму из нескольких слагаемых. Первое слагаемое (оно всегда положительное) - это произведение контурного тока и собственного сопротивления контура (сумма всех сопротивлений в данном контуре). Следующее слагаемое – это произведение смежного контурного тока на общее сопротивление двух контуров. Оно положительно, если контурные токи протекают через резистор в одном направлении или отрицательно, если в разном.
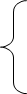
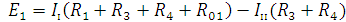
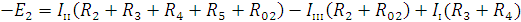
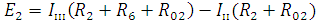
Подставляем в уравнения численные значения ЭДС и сопротивлений.
 |
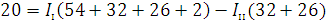
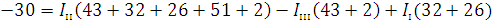
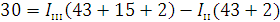
Решаем систему на ЭВМ, заполнив таблицу 1.2
Таблица 1.2
|
II, А |
III, А |
IIII, А |
E, В |
|
114 |
-58 |
0 |
20 |
|
-58 |
154 |
-45 |
-30 |
|
0 |
45 |
60 |
30 |
Решение системы находим по следующим формулам
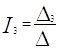 |
|||||||
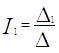 |
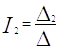 |
||||||
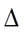 |
|
|
114 |
-58 |
0 |
|||
|
= |
-58 |
154 |
-45 |
= |
1082370 |
|
|
0 |
45 |
60 |
||||
|
|
20 |
-58 |
0 |
|||
|
= |
-30 |
154 |
-45 |
= |
199200 |
|
|
30 |
45 |
60 |
||||
|
|
114 |
20 |
0 |
|||
|
= |
-58 |
-30 |
-45 |
= |
18300 |
|
|
0 |
30 |
60 |
||||
|
|
114 |
-58 |
20 |
|||
|
= |
-58 |
154 |
-30 |
= |
527460 |
|
|
0 |
45 |
30 |
II= 0,1904A
III=-0,0295А
IIII= 0,4631A
Зная контурные токи, находим действительные:
I1= II=0,1904А
I2= II-III=0,1904-0,0295А=0,1610А
I3=III=-0,0295А
I4=IIII-III =-0,5221-0,0295=0,4926А
I5=-IIII=-0,5221А
Таблица 1.3 -Сравнение результатов по 1-му и 2-му способу вычисления
|
Метод расчёта |
I1, A |
I2, A |
I3, A |
I4, A |
I5, A |
|
Метод контурных токов |
0,1904 |
0,1610 |
0,0295 |
0,4926 |
-0,5221 |
|
Метод узловых и контурных токов |
0,1904 |
0,1610 |
0,0295 |
0,4926 |
-0,5221 |
1.3 Расчет электрических цепей методом узлового напряжения
Составляем частные схемы исходя из данных рисунка 1 (схемы содержат только одну ЭДС, остальные принять равные нулю). Выбираем направление частных токов:
Рисунок 1.1 – Первые частные схемы
Рисунок 1.2 – Вторая частная схема
Решаем первую частную схему:
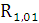 =
=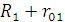 =56
Ом
=56
Ом
R3,4= R3+R4=58 Ом
R1,01,3,4=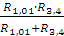 =28,5
Ом
=28,5
Ом
R1,01,3,4,5= =79,5
Ом
=79,5
Ом
R1,01,3,4,5,6
= =12,62Ом
=12,62Ом
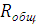 =
=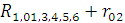 =55,62
Ом
=55,62
Ом
Решаем вторую частную схему:
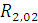 =
= =45
Ом
=45
Ом
R2,02,6=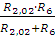 =11,25
Ом
=11,25
Ом
R2,02,5,6 =R2,02,6+R5=62,25 Ом
R3,4=R3+R4=58 Ом
RB,6=R6+RB=60,16 Ом
R2,3,4,5,6,02=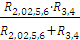 =30,025
Ом
=30,025
Ом
RОбщ. = R1+R2,3,4,5,6,02=84,025 Ом
2. Расчёт трехфазных электрических цепей переменного тока
В цепи, изображенной на схеме (рис 3.1), потребители соединены треугольником. Известно линейное напряжение … и сопротивление фаз …
Определить фазные, линейные токи, мощности активные, реактивные, полные мощности каждой фазы и всей цепи. Построить векторную диаграмму цепи.
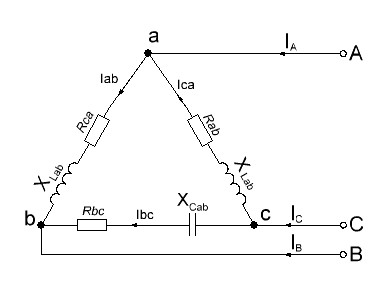
Рисунок 3.1 – Соединение потребителя треугольником.
При соединении трёхфазной цепи треугольником расчёт будем вести символическим методом.
1. Модули фазных напряжений при соединении треугольником равны линейным напряжениям
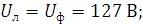 то
есть
то
есть 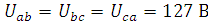 .
.
 совмещён с
действительной осью комплексной плоскости,
совмещён с
действительной осью комплексной плоскости,
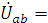
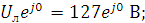
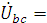
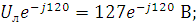
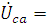
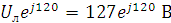
2. Вычислим комплексы фазных сопротивлений:
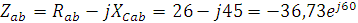
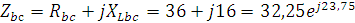
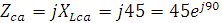
3. Определяем фазные токи:
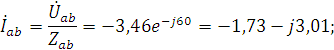
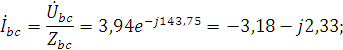
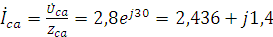 .
.
4. Находим линейные токи из уравнений, записанных по первому закону Кирхгофа для узлов a,b,c (рис. 3.1).
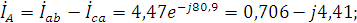
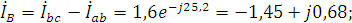

5. Вычисляем мощности каждой фазы и всей цепи:
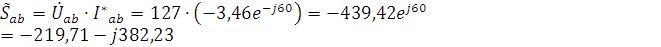
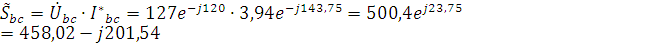
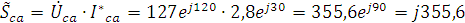
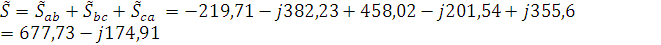
Перечень ТНПА
1. ГОСТ 2.104-2006 ЕСКД Основные надписи.
2. ГОСТ 2.747-68 ЕСКД Обозначения условно-графические в схемах. Размеры условно-графических обозначений.
3. ГОСТ 2.728-74 ЕСКД Обозначения условно-графические в схемах. Резисторы, конденсаторы.
4. СТП 7-2011 Правила выполнения текстовых документов.
5. ГОСТ 2.105-95 ЕСКД Общие требования к текстовым документам.
6. ГОСТ 1494-77 Электротехника. Буквенные обозначения основных величин.
7. ТР 2007/003/BY Единицы измерений, допущенные к применению на территории РБ.
8. ГОСТ 19880-74 Электротехника. Основные понятия. Термины и определения.
9. ГОСТ 2.710-81 ЕСКД Обозначения буквенно-цифровые в электрических схемах.
10. ГОСТ 2.721-74 ЕСКД Обозначения условно-графические в схемах. Обозначения общего применения.















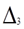
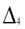
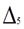
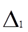
 (zip - application/zip)
(zip - application/zip)










